基于可拓云模型与模糊贴近度的电能质量评估研究

禹洪波，刘永波，黄滔滔，吴舟，罗远国，陈晓，熊炜，袁旭峰

（1.中国电建集团贵阳勘测设计研究院有限公司，贵州贵阳 550081；2.贵州电网有限责任公司贵安供电局，贵州贵阳 550025；3.贵州大学电气工程学院，贵州贵阳 550025）

0 引言

随着电力系统的快速发展，尤其是非线性和冲击负荷容量及数量的大量增加，电能质量问题日趋严重，不仅干预电网企业的安全经济运行，也会影响用电设备的正常工作[1-4]。如何准确有效地评估电能质量等级及其优劣排序，对于电能质量管控及电网稳定安全运行有重要意义。

现阶段电能质量评估方法主要分为以下2 类：一类是以机器学习为主的方法，此类方法所需指标数据量大，在实际的电能质量评估中能供应的数据较少，其应用受到一定限制，包括神经网络模型[5]和随机森林模型[6]等；另一类是以不确定性的推断为主的方法，以不确定的子证据作为基础出发推断得到在一定程度上具备不确定性又几乎合理的结果的方法，包括基于模糊集对分析的方法[7]，基于模糊理论的方法[8-9]、基于可拓理论的方法[10-12]、基于云理论的方法[13-15]、基于证据理论的方法[16-17]、基于可拓云理论的方法[18-20]等。其中，文献[7]提出一种基于模糊集对分析法的电能质量评估方法，应用灰色关联分析对层次分析法所求权重进行调整，避免了专家意见不一致导致权重分配出错，但仅计算了主观权重，评估结果缺乏客观性；文献[8]基于组合权重建立了电能质量模糊综合评价模型，利用组合权重法求得指标综合权重，避免了单一赋权的缺陷，但仅用模糊综合评价并依据最大隶属原则所得结果受主观性影响较大；文献[9]考虑了不同评价对象其权重不一致，提出了一种可变权重的电能质量模糊评价方法，但隶属度函数的确定存在主观性，且只考虑了模糊性；文献[10-12]通过物元理论解决了传统电能质量模糊评价中存在隶属度相近，难以区分及评估指标可能出现不相容的问题，但忽视了电能质量在等级边界处的模糊性和随机性；文献[13]构建了电能质量综合评估可变模糊云模型，该模型具备普适性，但当样本云模型与标准等级云模型在某个等级的云相似度相等或接近时，电能质量等级区分易存在偏差；文献[15]提出了一种基于状态变权和云模型的电能质量评估方法，避免了传统评估方法的不足，但当各观测点在同一质量等级时却不能进一步区分；文献[16-17]通过证据信息融合解决了单一子证据结论不一致，但信息融合时存在信息丢失影响评估准确性；文献[18-20]把可拓云理论结合应用到电能质量评估中，兼顾了2 种理论的特点，但以单一云熵计算方法得到云熵值，忽略了质量等级划分的模糊性，易导致评估结果冲突。文献[7-20]方法在电能质量评估应用中存在主观性、不确性、电能质量等级判断等问题。

本文把模糊贴近度引入到可拓云模型的电能质量评估方法中。首先，以可拓云理论为基础构建电能质量评估框架；其次，运用云熵优化兼顾2 种不同云熵计算方法的特点确定新的云熵值，进而得到改进可拓云模型来计算每个指标对应的质量等级关联度；最后，基于模糊贴近度的多目标分类算法对电能质量进行决策判断得到最终的评估结果。以某变电站10 kV 母线实测数据为例，验证了该方法的准确性和有效性。

1 电能质量评估框架

1.1 电能质量评估指标及其等级划分

依据国家电能质量相关标准，本文将频率偏差A1、电压偏差A2、电压波动A3、电压闪变A4、电压总谐波畸变率A5和三相电压不平衡度A66 项国家电能质量指标确定为此次评价指标，并把各指标等级划分为5 个级别，即H={H1，H2，H3，H4，H5}，分别为优质H1、良好H2、中等H3、合格H4、不合格H5，各指标对应的质量等级范围如表1 所示。

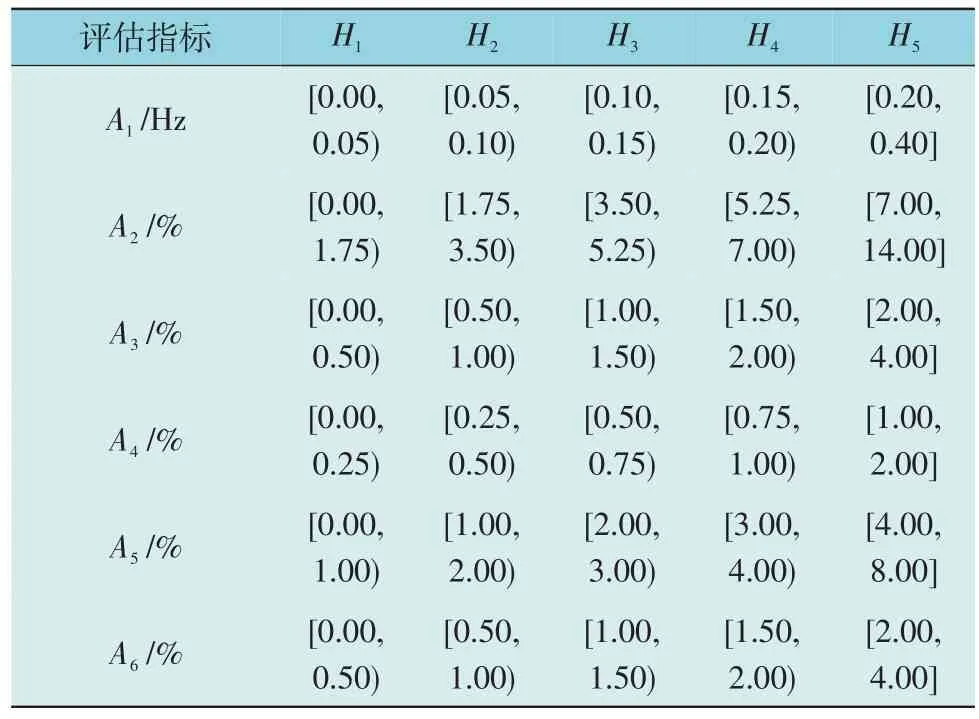
表1 电能质量各评估指标对应等级范围Table 1 Grade range corresponding to each evaluation index of power quality

1.2 可拓云模型

物元是指把研究对象N、对象的特征c、特征的量值v组合一起描述研究对象的基本元（即组成一个有序三元组），记作Q=(N,c,v)，Q为多维物元。传统基于物元理论的电能质量评估中未计及等级分类处的模糊性和随机性，但考虑到物元理论在处理评估指标中可能出现不相容问题及云模型在处理不确定性上的优势，把两者结合应用到电能质量评估中得到各评估指标对应的等级范围云模型。

可拓云模型是指物元Q=(N,c,v)中的v被正态云(Ex,En,Ee)[20]代替，其中Ex为云的期望；En为云熵；He为超熵，可表示如下：

式中：ci（i=1，2，…，n）为对象的第i个特征；（Exi,Eni,Hei）为第i个特征的量值v对应的正态云。

由式（1）说明可拓云模型主要是确定正态云的3 个参数(Ex,En,Ee)，其中Ex=(cmax+cmin)/2,cmin，cmax分别为电能质量等级范围上下限值，He=En/10。但3个参数中最重要是En的确定，该值既能表明电能质量指标等级范围概念对应的数值范围，又能影响质量等级评估的准确性。按不同的理解云熵的确定包括以下2 种原则：式（2）为“50%关联度”原则[21]；式（3）为“3En”原则[22]。

因式（2）确定的云熵在质量等级处偏向于模糊性，而式（3）确定的云熵在质量等级处倾向于分明性，这就可能导致电能质量评估结果发生冲突。为了综合上述2 种原则的特点，运用云熵优化算法[23]改进可拓云模型。

1.3 云熵优化算法

假设某电能质量评估指标的观测数据为xi(i=1,2,…,6)，质量等级总数为P，即有P组等级正态云。分别为期望和超熵集合；分别为式（2）、式（3）和优化确定的云熵集合，m(m1,2,···,p)为质量等级数，每个电能质量评价指标对应质量等级m云模型的关联度之差最大为：

为使电能质量各评估指标观测数据xi对应的P组质量等级云模型的和最小，利用式（5）计算得到新的云熵值：

将待评估电能质量指标的观测数据xi作为一个云滴，并以优化后的为期望值和He为标准差产生的随机数为E′n，则每个指标对应质量等级云模型的关联度k计算为：

式中：x为第i个指标的观测数据值。

由式（7）可得各指标观测数据xi与对应质量等级云模型之间的关联度矩阵K=[kmi]5×6，其中kmi为第i个指标与对应等级m云模型之间的关联度。

以1 组三相电压不平衡度观测数据为例，分别给出3 种不同原则确定的等级云模型（见图1—图3）。由图1 看出，以“50%关联度”原则为基础确定的云熵在质量等级处偏向于分隔模糊；由图2 看出，以“3En”原则为基础确定的云熵在质量等级处倾向于间隔分明；由图3 看出，以云熵优化为基础确定的云熵兼顾了两者的特征。

图1 以“50%关联度”原则为基础得到的等级云模型Fig.1 Grade cloud model based on principle of correlation degree of 50%

图2 以“3En”原则为基础得到的等级云模型Fig.2 Grade cloud model based on 3En principle

图3 以云熵优化为基础得到的等级云模型Fig.3 Grade cloud model based on cloud entropy optimization

在电能质量评估过程中，存在主观赋权[7，10]和最大隶属原则[9，16]判断导致结果偏差的缺陷，为避免以上影响，本文基于模糊贴近度的多目标分类算法决策判断电能质量等级。

2 基于模糊贴近度的电能质量等级确定

2.1 非对称模糊贴近度

定义电能质量评估中，5 个质量等级相应的模糊特征子集为Dj=（0，···，1，···，0），其中第j个分量为1，其余均为0，j=1，2，3，4，5。即D1=（1，0，0，0，0），D2=（0，1，0，0，0），D3=（0，0，1，0，0），D4=（0，0，0，1，0），D5=（0，0，0，0，1），非对称模糊贴近度N(k,D)的计算[24]为：

式中:n为总的等级数；vm为对应的质量等级；uk，uD分别为模糊子集k和D的关联度。

为避免直接利用式（8）判断导致结果存在偏差，需先进行k和D标准化处理，具体步骤见文献[25]。

由式（8）可得第i（i=1，2，…，6）个电能质量评估指标与5 个质量等级所对应特征子集的非对称贴近度Ri为：

式中：ki为第i个指标的模糊子集；为第i个指标标准化后对应的非对称贴近度。

则在所有评估指标下的非对称贴近度R为：

式中：Rji为第i个指标与对应等级j的非对称贴近度。

在电能质量实际评估中，如果仅依据每个评估指标与5 个质量等级的非对称贴近度来判断，易得出与实际不相符的评估结果，本文通过正负理想点（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）法定义参考等级，应用对称贴近度来度量贴近情况并判定得到结果。

2.2 正负理想点法

根据TOPSIS 法，定义参考等级分别为R+和R-[26]，其中R+为正理想等级，如式（11）所示，它表示在评估指标下对应5 个质量等级最贴近的状态；R-为负理想等级，如式（12）所示，它表示在评估指标下对应5 个质量等级最不贴近的状态。

为了得到电能质量评估指标下的评估结果，需度量电能质量等级集合Hm（m=1，2，…，5）中每个指标与正负理想等级的贴近度，为此记：

式中：Rj为各指标与等级j对应的贴近度。

利用对称贴近度公式来度量Rj与R+和R-是否贴近及对比差别。具体计算公式如下：

式中：uRj(uk) 为第i个指标与等级j的关联度；uR+(uk) 为第i个指标与正理想等级的关联度；uR-(uk)为第i个指标与负理想等级的关联度。

式中：Rm为等级m的贴近度。

通过式（16）即可得到电能质量为Hm等级。

3 电能质量评估流程

本文提出一种基于可拓云模型与模糊贴近度的电能质量评估方法，具体评估流程见图4。

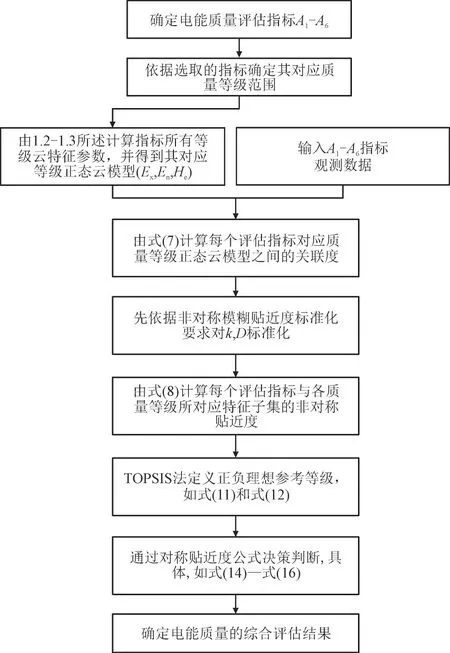
图4 电能质量评估流程Fig.4 Evaluation process of power quality

4 实例分析

以某变电站10 kV 母线中5 个观测点的实测数据为例，如表2 所示。以云熵优化为基础确定的电能质量评估指标对应等级云模型见表3；评估流程见图4。以观测点5 为例，由图4 流程计算可得全部电能质量评估指标下的非对称贴近度为:

表2 各观测点的实测数据Table 2 Measured data from each observation point

表3 电能质量各评估指标对应等级正态云模型Table 3 Grade normal cloud model corresponding to each evaluation index of power quality

通过式（11）和式（12）可得电能质量正负理想等级分别为：

依据式（13）—式（15）计算得到：

同样的计算方式可得：

通过式（16）进行判断，1.236 2＞0.955 2＞0.873 5＞0.859 8＞0.828 1，可知观测点5 的电能质量为H3等级。由表2 可知观测点5 的实测数据，除电压波动A3落在H5等级，其余指标均落在H3等级，结合各指标综合贴近度，本文将其判定为H3等级，符合电能质量的实际情况，验证了该方法的准确性。

为验证本文所提方法的准确性和有效性，分别与文献[7]模糊集对分析、文献[9]模糊综合评价、文献[16]物元和证据理论的方法进行对比，评估结果见表4。

表4 评估结果对比Table 4 Comparison of evaluation results

由表4 可知，本文方法所得评估结果与文献[16]物元和证据理论完全一致，但文献[16]方法中质量等级划分采用区间的形式，忽略了电能质量在等级边界处的模糊性和随机性；本文方法与文献[7]模糊集对分析除观测点2 外其余评估结果一致，文献[7]方法中只进行了主观赋权，缺乏客观实际，评估结果受主观性影响较大，由表2 可知观测点2 的实测数据除电压偏差A2和电压闪变A4落在H5等级，其余指标均落在H4和H3等级，结合各指标综合贴近度将其判定为H4等级更加合理；本文方法与文献[9]模糊综合评价除观测点4 外其余评估结果也一致，文献[9]方法中受到最大隶属原则判断导致结果偏差的影响，由表2 可知观测点4 除电压波动A3和电压总谐波畸变率A5落在H4等级，其余指标均落在H3等级，结合各指标综合贴近度将其判定为H3等级更加合理，验证了本文所提方法的准确性。

为进一步区分各观测点在同一等级下的电能质量情况，通过比较观测点对应的综合贴近度来划分，以观测点1、观测点2、观测点3 为例，文献[7，9，16]在得出评估结果均为H4等级后，并没有进一步区分3 个观测点的电能质量情况，通过式（13）-式（16）计算得到观测点1、观测点2、观测点3 的综合贴近度，如表5 所示。

表5 3个观测点的综合贴近度Table 5 Comprehensive proximity degree of three observation points

由表5 可知，3 个观测点对应各等级贴近度满足以下关系：观测点1（1.126 3＞1.105 3＞0.960 1＞0.766 7＞0.766 6），观测点2（1.101 3＞1.017 8＞0.998 3＞0.797 9＞0.797 5），观测点3（1.124 7＞1.113 7＞0.934 7＞0.783 2＞0.783 1），由式（16）判断可知3 个观测点均为H4等级。通过对分析可知，3 个观测点最大贴近度均在H4等级，但观测点1 的次最大贴近度在H3等级，观测点2 和观测点3在H5等级，说明观测点1的电能质量有从H4等级向H3等级倾斜的趋势，观测点2 和观测点3 有向H5倾斜的趋势，由此表明观测点2 和观测点3 的电能质量均劣于观测点1；又因观测点3 的次最大贴近度大于观测点2，说明观测点2向H5倾斜趋势的可能性小于观测点3，由此表明观测点3 的电能质量劣于观测点2。最终得到3 个观测点的电能质量由劣到优排序为：点3 劣于点2 劣于点1。

同样的划分方法可得，观测点4 的电能质量劣于观测点5，由表2 的实测数据可知，观测点5 的频率偏差A1、电压偏差A2、电压总谐波畸变率A5、三相电压不平衡度A6均小于观测点4，结合各指标的综合贴近度，观测点4 应劣于观测点5，验证了本文所提方法的有效性。最终得到全部观测点的电能质量由劣到优排序为：点3 劣于点2 劣于点1 劣于点4 劣于点5。

5 结论

本文提出了一种基于可拓云模型与模糊贴近度的电能质量评估方法。应用云熵优化算法兼顾2种不同云熵的特点确定新的云熵值，避免了评估结果冲突的可能性；把模糊贴近度引入到可拓云模型的电能质量评估方法中，避免了权重求取和最大隶属原则所附带主观性的影响，且仅需通过比较各观测点的贴近度就可进一步区分同一等级下的电能质量情况。实例分析表明，采用本文所提方法得到的评估结果符合各观测点实际电能质量情况，验证了本文所提方法的准确性和有效性。