基于合作博弈的多区域综合能源系统优化调度

张明光，王文婷，陈大为

（兰州理工大学电气工程与信息工程学院，甘肃兰州 730050）

0 引言

随着各行各业能源需求的增长以及化石能源短缺、环境污染等问题的出现，传统以化石能源发电的大电网面临着严峻的挑战[1-3]。在此背景下，综合能源系统（Integrated Energy System，IES）通过集成冷、热、电多能及分布式电源，有效提高能源利用效率，减少温室气体排放及对化石能源的依赖[4-6]。

目前，针对电、气、冷、热多能融合的IES 的统一建模、系统优化，已成为学术界关注的热点之一。文献[7-8]以综合能源系统成本最小为目标函数构建了含风、光、气、网联合供电、供热（冷）的IES 调度模型。文献[9-10]提出计及热能输运动态特性的IES优化调度方法。文献[11-13]提出基于热电联供灵活热电比的区域IES 多目标优化调度方法。基于大多数IES 无法完全自给自足运行，需要从电网获得额外的电能供应，有学者提出利用能源互联系统提升IES 独立性[14-16]。如文献[15]中不同区域IES 间进行电、热能交互的能源互联系统，与独立运行的IES相比总成本可降低19.2%。

然而，现阶段针对多区域IES 能源互联的研究多是从联盟层面进行优化，很少有研究互联系统利益分配问题。实际上，多区域IES 选择能源互联的目的是实现自身利益最大化[17]。因此，为了维护能源互联系统稳定性并保证IES 个体利益，有必要协调整体和个体之间的利益关系。因此，本文在多区域IES 能源互联体系下，重点研究合作博弈联盟利益分配机制：构建了不同区域IES 能源互联系统日运行成本模型；从概率角度提出了多区域IES 合作博弈分配机制；通过算例分析验证了所提分配机制的有效性。

1 系统数学模型

多区域IES 结构如图1 所示，不同区域IES 通过微热网和微电网实现能量交互，从而改善整个能源网络的经济效益。每个IES 均配备了冷热电联产系统（Combined Cooling Heating and Power，CCHP）和分布式电源。

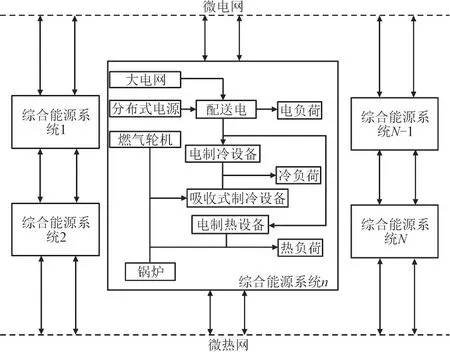
图1 多区域IES能源互联系统Fig.1 IES energy interconnection system for multiple regions

1.1 IES模型

假设整个能源互联网中共有N个IES，其集合α={1,2,…,N}。IES 的设备模型主要包括：

1）微型燃气轮机。微型燃气轮机在发电的同时可将余热回收，其电功率和热回收功率可表示为：

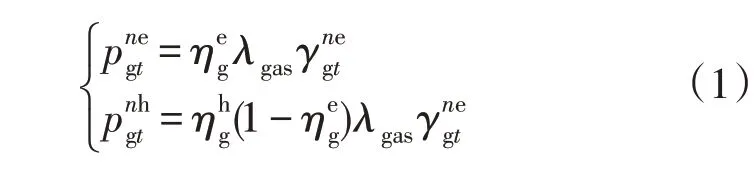
2）锅炉。当燃气轮机的余热不能满足用户热需求时，可通过锅炉进行补充。锅炉的热功率为：

3）多能转换设备。IES 系统涉及多能流转换，考虑到转换过程中能量损失，其模型可表示为：

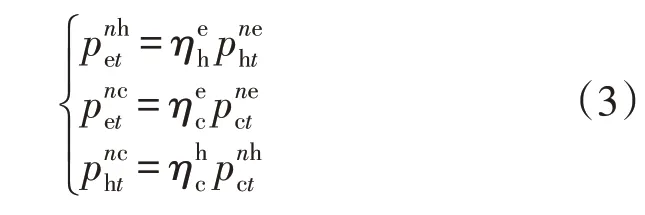
4）分布式电源。新能源发电预测方法包括：用于光伏预测的最大功率点跟踪方法[18-19]和；用于风电预测的不确定性分析[20-21]。假设分布式电源输出功率为：

式中：为分布式电源输出功率；为t时段内第n个IES 的电功率；T为总时段。

5）需求响应（Demand Response，DR）模型。IES 可通过DR 技术提高能源利用效率并降低用户能源成本，本文假设IES 内部用户愿意参与DR。

（1）刚性负荷。该负荷为不可转移负荷，其负荷需求一般较为固定。假设第n个IES 的刚性负荷需求为：

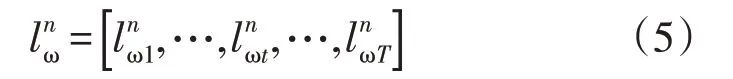
式中：为第n个IES 的刚性负荷需求；为t时段内第n个IES 的刚性负荷需求。

（2）柔性负荷。该负荷对用能时段不敏感，将其转移至其他时段对用户影响较小。其DR 模型为：

1.2 IES成本模型

IES 各成本模型如下：

1）投资成本。IES 需支付设备投资成本，考虑设备的折现率和使用寿命，每天的投资成本为：

式中：为第n个IES 的投资成本；i=1～4 分别为燃气轮机、锅炉、能源转换设备及分布式电源；r为折现率；yi为设备i的使用寿命；为设备投资成本；为安装容量。

2）运维成本。IES 须支付系统设备运维费用，假设运维成本与各设备的输出功率成线性相关，即：

3）天然气成本。天然气成本主要来自微型燃气轮机和锅炉，可以通过式（9）计算：

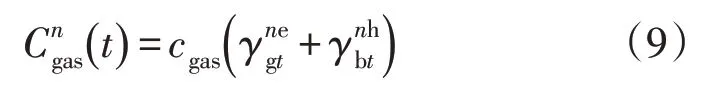
4）电能成本。IES 可从公共电网购买电能，假设电网采用分时电价。因此，第n个IES 的电能成本为：

5）能源输送成本。不同IES 能量交互需考虑能源输送成本，尤其在传输损耗和管道维护的热传输过程中。假设输送成本与输送能量和距离相关：

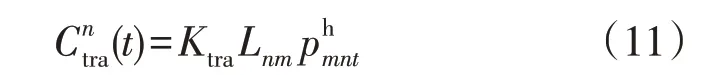
2 多区域IES合作博弈

基于合作博弈，各IES 会形成合作联盟，并以联盟运行费用最小为目标进行用能优化调度安排。

2.1 IES联盟优化模型

由1.2 节可知，IESn（∀n∈α）的日运行费用为：

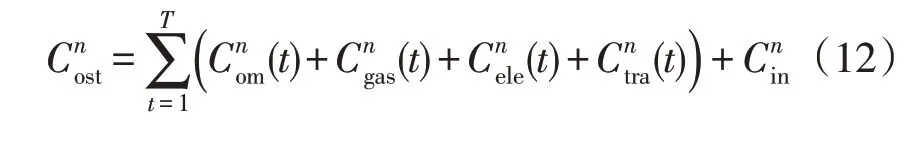
参与合作博弈的IES 以联盟的日运行成本最低作为优化目标。因此，定义多区域IES 合作博弈：假设集合S⊆α是α中的k个IES 组成的合作联盟。假设v为联盟的特征函数，即联盟的收益[15]：

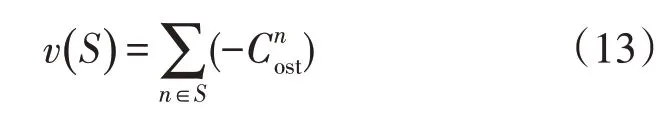
式中：v(S)为联盟S的收益。

在合作机制下，联盟中的IES 可以交换热能和电能，最大化联盟的收益v(S)，根据IES 在联盟中的贡献度将收益分配至各IES。

2.2 IES运行约束

为保证IES 可靠运行，当多区域IES 追求联盟最大收益时，应满足以下约束条件。

2.2.1 相等约束条件

1）功率平衡约束：

2）热平衡约束：

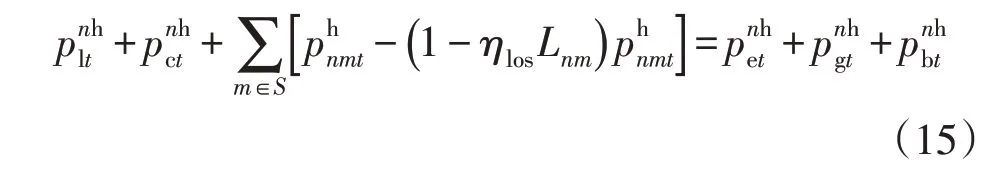
3）冷平衡约束：

2.2.2 不等约束条件

1）输出约束：

式中：为t时段内设备i的能量输出；为i设备出力上限。

2）能量交互约束：

式中：Ne，Nh分别为任意2 区域IES 电能、热能的交互上限；为二进制变量，衡量2 个区域是否交换能量。

式（19）表示2 个区域IES 不能同时交换能量。

3 合作博弈分配机制

合作博弈分配机制根据个体对联盟的边际贡献将利益重新分配至每个IES，使其自身利益最大化。

3.1 分配机制构建

首先，需要定义联盟中各IES 边际贡献。由2.1节可知，k个IES 构成1 个联盟S，假设m（m∉S）独立于联盟S。联盟的边际贡献可定义为[22-23]：

假设联盟S形成概率为Pm(S)，合作博弈中第m个IES 的收益分配可表示为：

式中：为合作博弈中第m个IES 的收益分配；的期望值；S⊆α{m} 表示S是α（其中{m} 独立于α）中的k个IES 组成的合作联盟。

可通过式（22）计算联盟形成概率：

式中：AS为联盟S拥有k个IES 的事件；Pm(AS)为相应概率；Pm(S|AS)为在联盟有k个IES 的条件下形成联盟S的条件概率。

结合式（21）、式（22），第m个IES 的收益可表示为：

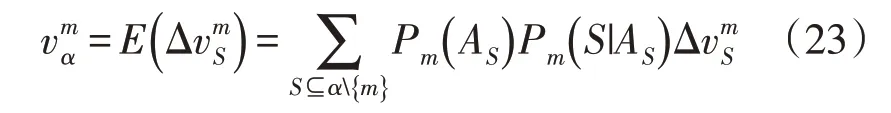
进而，联盟中所有IES 的收益可表示为：

式中：Vα为集合α中所有IES 的收益。

3.2 分配机制特殊情况

合作博弈中各IES 收益将条件概率进行重新分配。当∀n∉S且Pn(AS)和Pn(S|AS)给定不同值时，会产生不同的分配方法。

1）Shapley 分配[24-25]。假设AS服从（0，N-1）上的均匀分布，

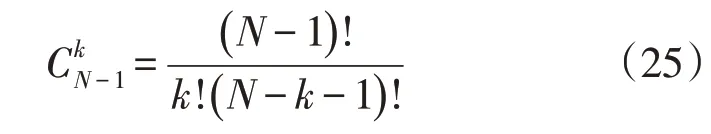
因此，式（23）也可表示为：

2）Banzhaf 分配[26]。假设AS服从二项式分配：

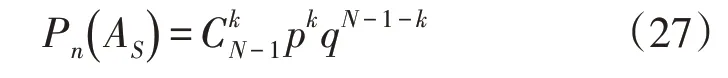
式中：p为IES 参与合作的概率，且q=1-p。

因此，式（23）也可表示为：

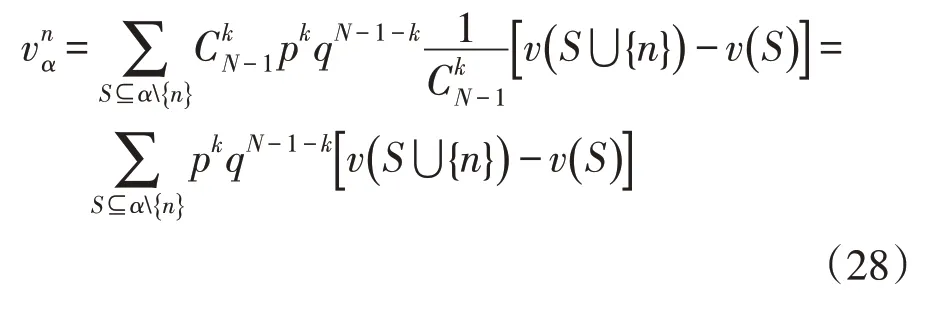
4 仿真研究

4.1 能源互联系统参数

假设能源互联系统中有工业园区、商业区和居民区。各IES 均配备了CCHP 系统和光伏发电，工业园区另配备了风力发电。本算例针对典型日进行分析：谷时段（00:00—7:00）时Celet=397.6 元/MWh，平时段（22:00—24:00）时Celet=580.7 元/MWh，峰时段（7:00—22:00）时Celet=1025.2 元/MWh。天然气价格Cgas为3 元/m3。IES 设备参数如表1 所示。图2为3 个区域IES 不可转移用能需求，可以看出3 个区域IES 能源需求具有差异性，工业园区用电需求高，商业区用热需求低，居民区峰谷差明显。假设居民社区的电动汽车属于可移动负荷，其总能源需求为8.5 MWh（约占不可转移负荷的20%），用电时段为19:00—7:00。

图2 各区域IES用能需求Fig.2 Energy demand of IES in different regions

表1 区域内IES的设备参数Table 1 Equipment parameters of IES in each region

4.2 联盟IES优化调度结果

图3 所示为3 个区域IES 用电调度计划，其中，负值表示该区域向外输出的能量，用电需求量为电负荷及电制冷机需求总和。

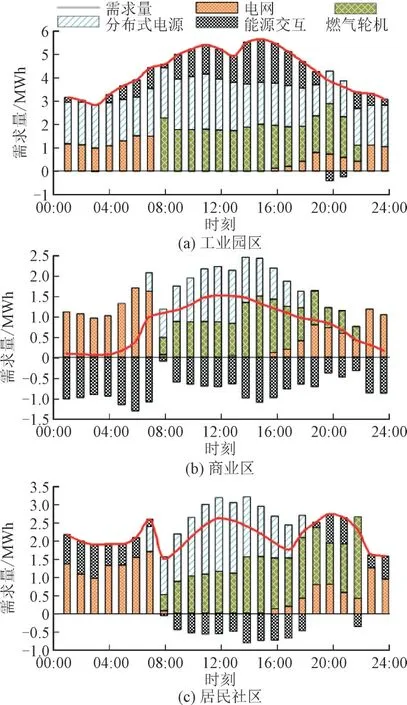
图3 各区域IES电调度计划Fig.3 Power dispatching plan of IES in different regions

由图3 可知，3 个区域在24 h 内均存在能量交互现象。由于工业园区对电负荷需求较高，商业区和居民社区将剩余电能全部输送给了工业园区，从而降低联盟总购能费用。此外，3 个区域的微型燃气轮机主要在7:00—22:00 期间运行，而00:00—7:00主要通过从电网购电来满足各区域用电需求。这是因为00:00—7:00 电网电价要低于燃气轮机发电成本。从DR 角度看，由于用电低谷时段电价最低，因此电动汽车的充电时段转移到了00:00—7:00。因此，利用DR 和区域IES 互联，不仅可以降低联盟的成本，还可以减少电网峰谷差。

图4 所示为3 个区域IES 用热调度计划，用热需求量为热负荷及吸收式制冷机需求总和。燃气锅炉提供的热量、余热和热交互可以满足能源互联系统的热需求。由于工业园区燃气轮机在发电过程中会产生大量的余热，因此工业园区的热能成为商业区和居民社区的重要来源。在07:00—21:00期间，工业园区为其他2 个区域共提供17.2 MWh等效的热能，有效降低了能源购买成本。综合电、热能调度结果可知，利用不同区域IES 间多种能源需求的互补特性，可以实现能源的有效利用，进而降低能源成本。

图4 各区域IES热调度计划Fig.4 Heat dispatching plan of IES in different regions

4.3 联盟IES利益分配

根据4.1 多能优化调度结果，可获得3 个区域IES 总运行费用。本节通过Shapley 和Banzhaf 2 种分配机制对联盟总费用进行分配。工业园区、商业区和居民社区构成集合{1，2，3}，可形成7 个联盟。当存在多个联盟时，每个联盟独立优化其日运行费用。经计算，集合{1}形成的联盟的日运行费用，集合{2}形成的联盟的日运行费用，集合{3}形成的联盟的日运行费用，集合{1，2}形成的联盟的日运行费用，集合{1，3}形成的联盟的日运行费用，集合{2，3}形成的联盟的日运行费用，集合{1，2，3}形成的联盟的日运行费用。基于日运行费用，可根据式（20）计算联盟中各区域IES 边际贡献，结果如表2 所示。其中，k为0，1，2 分别代表联盟S由0 个、1 个、2 个IES 组成，{∅}代表联盟S为空集。

表2 联盟中每个地区的边际贡献Table 2 Marginal contribution of each region in coalition

根据边际贡献，由Shapley 和Banzhaf 2 种分配机制可计算出各区域IES 日运行费用：=1.72×105元。

与IES 参与合作博弈之前费用相比，参与合作后的工业园区费用减少了0.8×104元，商业区减少了0.43×104元，居民社区减少了0.3×104元。由此可以看出，参与合作后，各区域IES 费用均有所降低，从而保证了合作联盟的稳定性。

5 结语

本文提出了一种多区域IES 能源互联体系下的利益分配机制。通过建立合作博弈模型，以最小化联盟日运行费用为目标，在多区域IES 之间进行日前调度。从概率角度提出联盟个体利益分配机制，根据个体在联盟中的边际贡献来分配联盟利益。与传统独立IES 相比，能源互联系统可以有效降低联盟运行费用。同时，通过所提出的利益分配机制，可将联盟总费用有效分配至各区域IES，从而保证了联盟利益分配的公平性与合理性。