煤矿提升机提升位置的精确指示与控制

付中华

(山西省长治经坊煤业有限公司，山西省长治市，047100)

0 引言

近年来，我国煤矿采煤机械化程度逐渐走高。对于煤矿安全生产中的一些关键设备，例如煤矿提升机提升位置指示器，需要对提升容器运行位置进行精确指示。煤矿提升机提升位置指示器是一种用来指示提升机罐笼等提升容器在提升井中状态的仪器，也是提升机的重要组成部分[1]。目前，国内的煤矿提升机提升位置指示器为牌坊式深度指示器和圆盘深度指示器。它们的信号都是从主轴直接获取，以此推测提升容器的位置 ，然后通过自整角机来调控其运动的位置。这种控制方式误差较大、精度不足，不仅威胁到生产效率，更是埋下了很多的安全隐患[2]。磁偶式无杆气缸具有定位精度高、安装方便、构造简单、价格低廉等优点[3]，因此非常适用于驱动煤矿提升位置指示器的运行。目前，影响气动位置伺服控制精度的主要因素是：气动系统的非线性特性，主要表现在比例方向控制阀质量流量方程的非线性[4]、系统数学模型的非线性[5]与磁偶式无杆缸运动时摩擦力的非线性；合适的控制策略，合适的控制策略可以对气动系统数学模型误差进行弥补，且可以进一步提高气动伺服系统的位置控制精度[6]。为了提高气动系统的位置控制精度，学者们一般将气动系统的数学模型进行线性化。但如果模型的运动距离与最初预定的工作范围相差较大时，其设计与分析就失去了意义[7]。

1 气动位置伺服控制系统的研究现状

目前，国内外学者对气动系统的非线性特性与控制方法进行了大量的研究，并且取得了不小的成果。美国加州大学的博罗·詹姆斯(Borrow Jams)[8]运用试凑法得出：气缸内排出气体的质量流量与比例阀的控制电压呈二次曲线关系；维瓦罗(Virvalo)[9]在分析控制阀物理结构的基础上，研究了控制阀内部的饱和、滞后、泄漏、零位偏移等非线性现象；柏艳红[10]与ZHANG Y等[11]通过对比例方向控制阀与摆动气缸的物理特性进行分析与研究，建立并验证了摆动气缸非线性位置伺服控制系统的数学模型的正确性；石炳存[12]通过对重要气动元件的特性进行分析，建立了有杆气缸位置伺服控制系统的非线性数学模型，并且反映出了气动位置伺服控制系统的特性；HSU S C[13]基于现有PID控制闭环系统，设计了混合模糊重复控制方法与前馈补偿器和零相位误差跟踪控制器，展现出了很高收敛速度与稳定性；詹长书[14]通过对气动位置伺服控制系统以及系统中气动元件进行研究，建立了气动系统的数学模型并运用模糊PID控制算法，系统的自适应能力得到了改善；柏艳红等[15]通过运用PID与气动辅助限位控制算法，提高了摆动气缸位置伺服控制系统的稳定性与位置控制精度。

虽然国内外学者已经对气动系统的非线性特性与控制方法进行了大量的研究，但对于磁偶式无杆气缸非线性位置伺服控制的研究几乎没有。因此，以磁偶式无杆气缸和比例方向控制阀为研究对象，建立了磁偶式无杆气缸非线性位置伺服控制系统的数学模型，并通过设计RBF神经网络优化PID控制器，进一步提高了磁偶式无杆气缸非线性位置伺服控制系统的位置控制精度。

2 实验平台的搭建

为了顺利地搭建气动系统的实验平台，首先需要了解气动系统的工作原理，以磁偶式无杆气缸为控制对象的气动位置伺服控制系统的工作原理如图1所示。

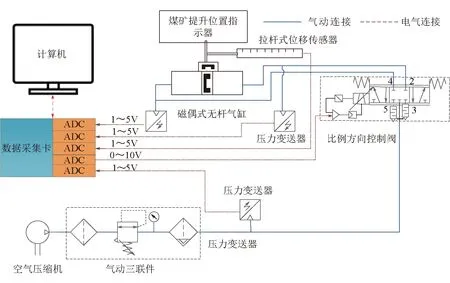
图1 磁偶式无杆气缸位置伺服控制系统原理

该气动系统的工作原理是：首先空气压缩机通过其内部的活塞往返运动，会产生一定量的气体。然后气动三联件会对气体进行干燥、净化，压力变送器可以检测气缸两端的气体压力。通过改变比例方向控制阀的控制电压，可以实现磁偶式无杆气缸的往返运动，进而可以带动提升位置指示器运动。拉杆式位移传感器可以用来检测磁偶式无杆气缸运动的距离，检测到的数据将会通过数模转换，最后在计算机上显示出来。根据上述实验原理搭建的实验平台如图2所示。

图2 磁偶式无杆气缸位置伺服控制系统实验平台

3 磁偶式无杆气缸非线性位置伺服控制系统数学模型的建立与验证

3.1 比例方向控制阀质量流量方程的建立

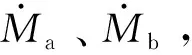
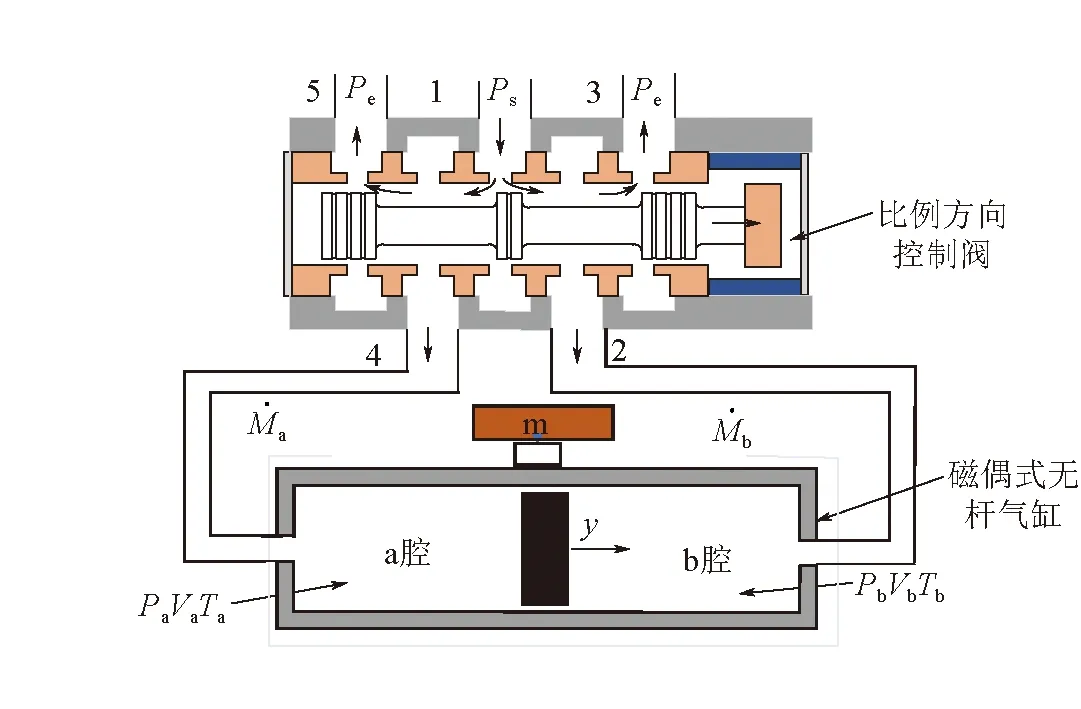
图3 阀控气缸系统的气体流动原理

阀控缸系统具有十分复杂的数学模型，为了使阀控缸系统的数学模型更加简化，本文做出了以下几点假设[16]：

(1)假设空气为理想型气体；

(2)气动系统中空气的流动为等熵绝热；

(3)容腔中气体温度与压力处处相同；

(4)气缸在运动过程中，腔室内没有与外界发生热交换。

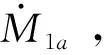
式中：h0——阀芯与套筒之间的间隙；

dh——套筒的内径，取0.006 023 m；

ds——阀芯的台肩外径，取0.006 m；

R——气体常数，为8.314 32×103N·m/(kg·K)；

S——阀开口有效面积，mm2；

μ——气体微元粘性系数，取0.000 018 3 Pa·s；

L0——间隙初始长度，m；

xv——阀芯位移，m；

b——临界压力比，为0.528；

Ts——供气温度，K；

κ——等熵指数，为1.4；

Cv——流量系数；

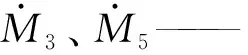
3.2 磁偶式无杆气缸能量方程与压力微分方程的建立

根据热力学第一定律，可以推导出磁偶式无杆气缸的能量方程为：

κRTiadMa=VadPa+κPadVa

(5)

式中：Tia——进入气体的温度，K;

dMa——进入气体的质量，kg。

阀芯正向移动时，磁偶式无杆气缸a腔与b腔室的压力微分方程分别为：

(6)

3.3 磁偶式无杆气缸动力学方程的建立

由于Stribeck摩擦模型[17]在描述物体运动的摩擦力时，可以达到90%以上的精度。因此，本文在描述磁偶式无杆气缸运动的摩擦力时，运用了Stribeck摩擦模型。其数学模型如下所示：

(7)

式中：Ff——摩擦力，N；

Fs——物体所受到的最大静摩擦力，N；

v——速度，m/s；

Fe——物体所受到的外力，N。

(8)

式中：B——粘性摩擦系数；

Fc——库仑摩擦力,N；

vs——Stribeck的临界速度,m/s；

δs——经验系数，一般为0.5～2.0。

动力学方程为：

A(Pa-Pb)=ma+Ff

(9)

式中：A——活塞的有效面积，取0.000 491 m2；

a——气缸运行的加速度,m/s2。

根据建立的质量流量方程、能量方程、压力微分方程、动力学方程可以构建磁偶式无杆气缸位置伺服控制系统的数学模型。将上述所有方程代入到MATLAB中进行仿真，然后进行定位实验验证，施加一个58 mm的阶跃信号，实验与仿真的结果如图4所示。

然后再进行轨迹跟踪实验，施加一个正弦信号，初始值为38 mm，频率为2 rad/s，幅值是15.2 mm。实验与仿真的结果如图5所示。

从图4与图5中可以看出，实验曲线与仿真曲线的运动趋势基本一致，不仅可以说明数学模型的正确性，也充分反应了数学模型的有效性。

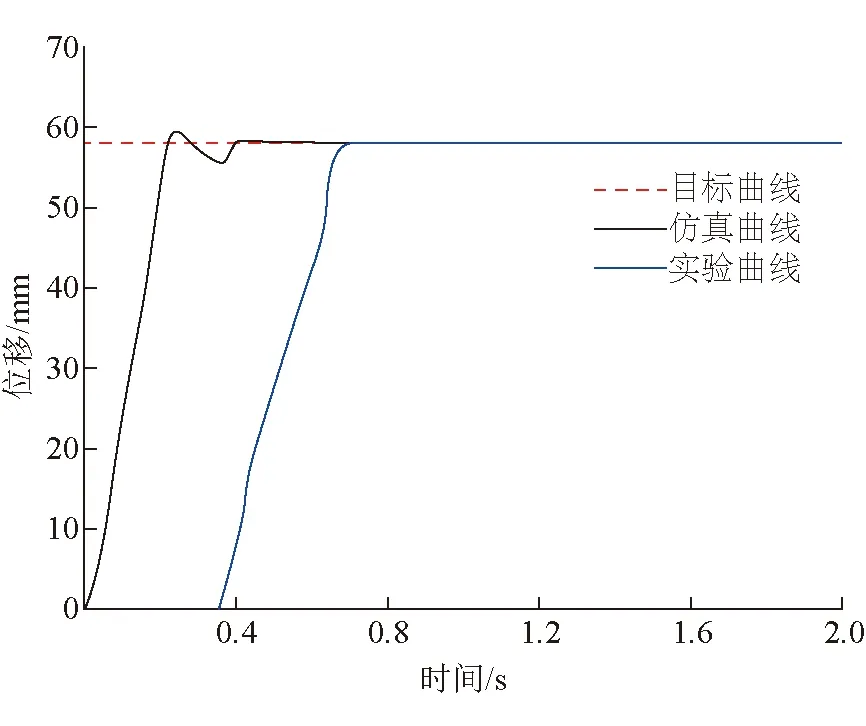
图4 定位实验仿真曲线

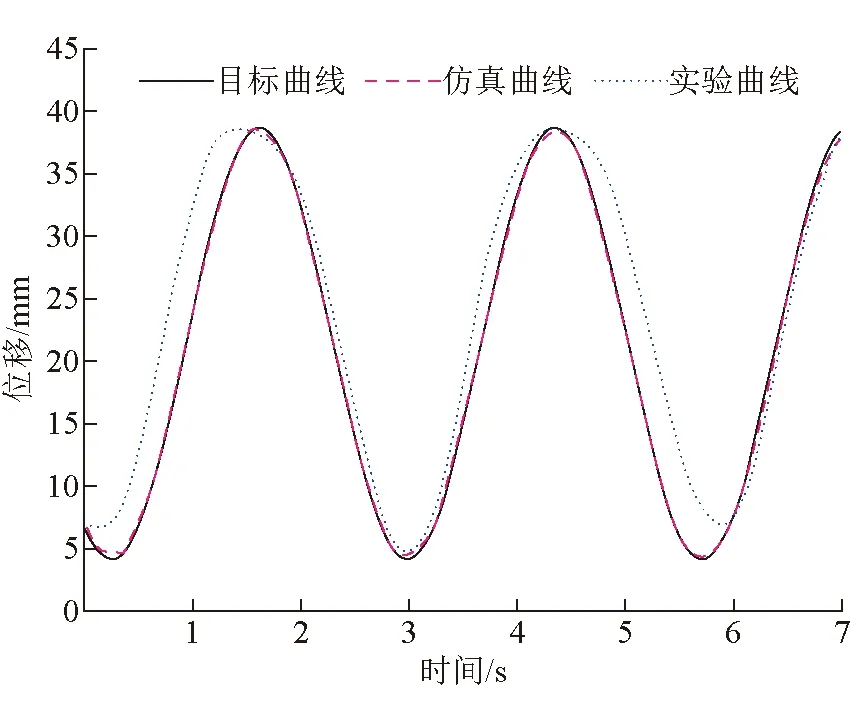
图5 轨迹跟踪实验仿真曲线

4 基于RBF神经网络优化PID的控制实验

4.1 RBF神经网络的基本原理及构成

麦卡洛赫(MCCULLOCH W)和皮特斯(PITTS W)在1943年提出了神经元的数学模型[18]，1985年，鲍威尔(POWELL)[19]提出了多变量插值的径向基函数(RBF-Radial Basis Function)。1988年，洛韦(LOWE)等将RBF应用于神经网络设计，并将RBF神经网络与BP神经网络进行了对比[20]，最后揭示了二者的关系。RBF神经网络具有学习速度快，简单易懂、泛化性能较强和计算简便等特点。RBF神经网络与BP神经网络相比，具有更强的生命力。因此，在某些领域内RBF神经网络逐渐替代BP神经网络。

RBF神经网络由输入层、隐含层以及输出层构成。输入层可以将神经网络与外界相连接，网络和外部的输入构成信号神经元；隐含层神经元是一种中心点径向对称衰减的非负非线性函数，输入层到隐含层的变换是非线性[21-22]。输出层是对所有输入信号做出响应，隐含层到输出层是线性的，并且为输出层的激活信号提供响应。图6描述了一个具有n个输入节点、m个隐层节点以及k个输出节点的3层RBF神经网络结构。

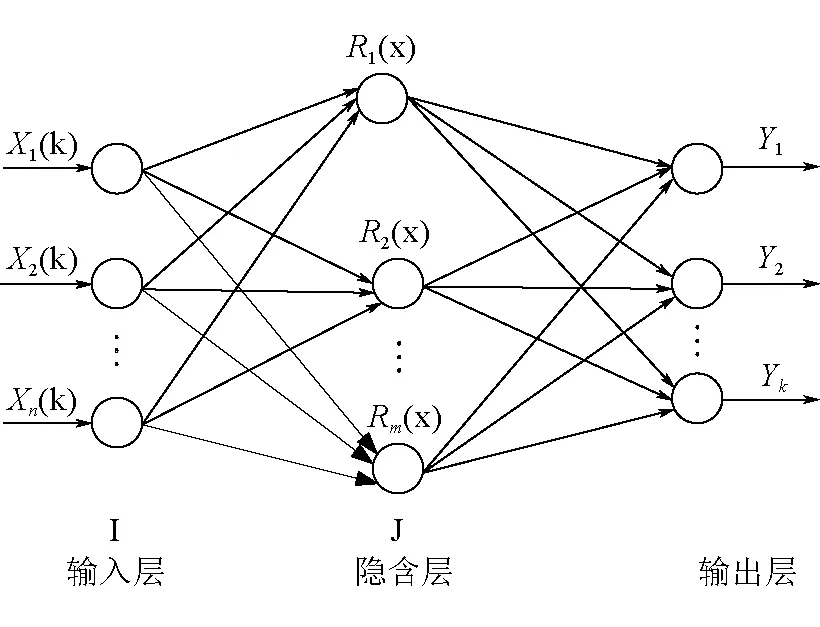
图6 RBF神经网络结构

假设输入层X=[x1,x2,…，xn]，隐含层到输出层的权值为W=[w1,w2,…，wj]T，径向基向量为hj，神经网络的输出为ym。径向基向量的数学表达式为：

hj=fj(x1,x2,…，xn)

(10)

式中：fj——径向基函数，j=1,2,3,…，m。

hj到ym的映射，表达式为：

(11)

高斯函数具有结构简单与对称性好等优点。因此，本文的径向基函数设为高斯函数，如式12所示：

(12)

式中：cji——隐含层神经元的中心点，cji=[cj1,…,cjn]，i=1,2,…，n；

bj——高斯函数的宽度向量，bj=[b1,…,bm]T。

4.2 RBF神经网络优化PID控制器的设计

由于阀控缸系统的非线性特性非常复杂，因此将与RBF神经网络与PID控制相结合。利用RBF神经网络的自学习特性实现对PID参数的优化，来提高位置的精确控制。PID控制器如式13所示：

(13)

式中：u(k)——PID控制器在第k次采样时的输出；

e(k)——第k次采样时输入的误差；

e(k-1)——第k-1次采样时输入的误差；

e(k-2)——第k-2次采样时输入的误差；

Kp——比例系数；

Ki——积分时间常数；

Kd——微分时间常数。

基于RBF优化PID控制器的磁偶式无杆气缸控制结系统构如图7所示。rin(k)为给定的输入信号，yout(k)为煤矿提升位置指示器输出的位置信号。PID控制的输入为误差信号ec(k)，RBF神经网络的输入为煤矿提升位置指示器的位移信号与PID控制器的输出，RBF神经网络的输出是对PID控制参数的补偿。

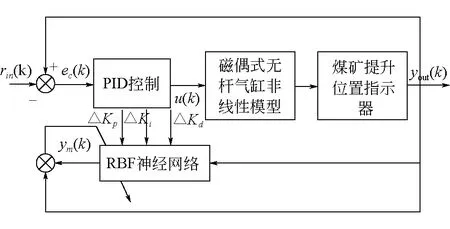
图7 基于RBF优化PID控制器的磁偶式无杆气缸控制结系统构

4.3 基于RBF神经网络优化PID控制策略的定位实验

构建的RBF神经网络隐含层的节点数为6个，设置好相关节点的参数，给定一个目标位置为58 mm的阶跃信号，其位置的控制效果如图8所示。

图8 基于RBF神经网络优化PID定位实验位移曲线

基于RBF神经网络优化PID的定位实验的位置控制精度明显优于传统PID定位实验的位置控制精度，如图9所示。从图9中的误差曲线可以得出：传统PID控制策略的位移误差范围为-0.129 0～-0.145 6 mm，基于RBF神经网络优化PID控制策略的位移误差范围为-0.004 ～0.004 mm。

图9 基于RBF神经网络优化PID定位实验位移误差曲线

基于RBF神经网络优化PID定位实验速度曲线如图10所示。从图10可以看出基于RBF神经网络优化PID的定位实验的反应速度稍慢于传统PID控制策略。

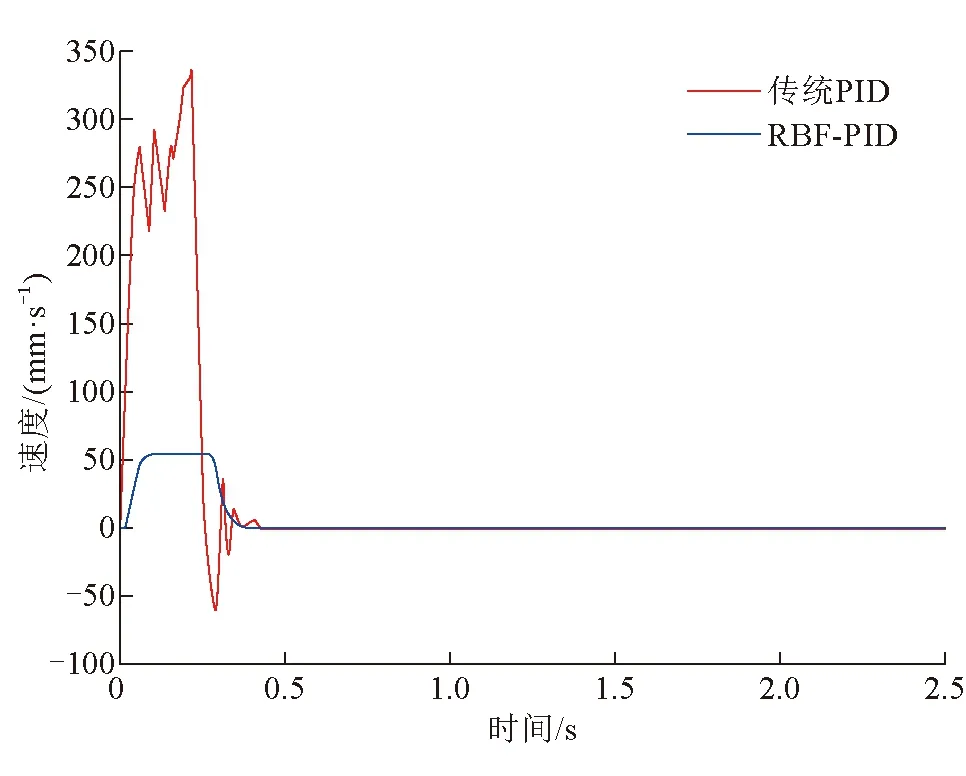
图10 基于RBF神经网络优化PID定位实验速度曲线

4.4 基于RBF神经网络优化PID控制策略的轨迹跟踪实验

在MATLAB的算法仿真模型中，给定一个正弦信号，初始位置是23.4 mm，频率为2 rad/s，幅值是15.2 mm。设置好RBF神经网络的初始参数，并对控制器的PID参数进行优化，其轨迹跟踪效果如图11所示。

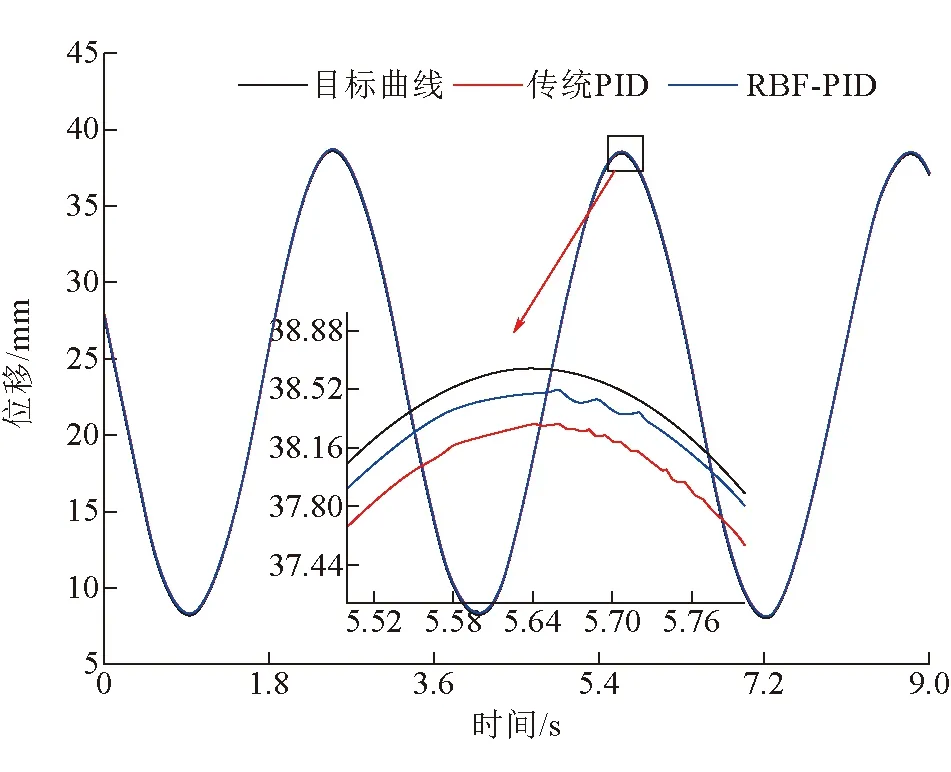
图11 基于RBF神经网络优化PID轨迹跟踪位移曲线

基于RBF神经网络优化PID轨迹跟踪位移误差曲线如图12所示。从图12中的位移误差曲线可以得出，传统PID控制策略的位移误差范围是-0.427 ～ 0.545 mm，基于RBF神经网络优化PID控制策略的位移误差范围是-0.361 ～0.249 mm，基于RBF神经网络优化PID控制策略的轨迹跟踪精度最高。基于RBF神经网络优化PID轨迹跟踪速度曲线如图13所示。从图13中可以看出，基于RBF神经网络优化PID控制策略的速度波动范围优于传统PID控制策略。

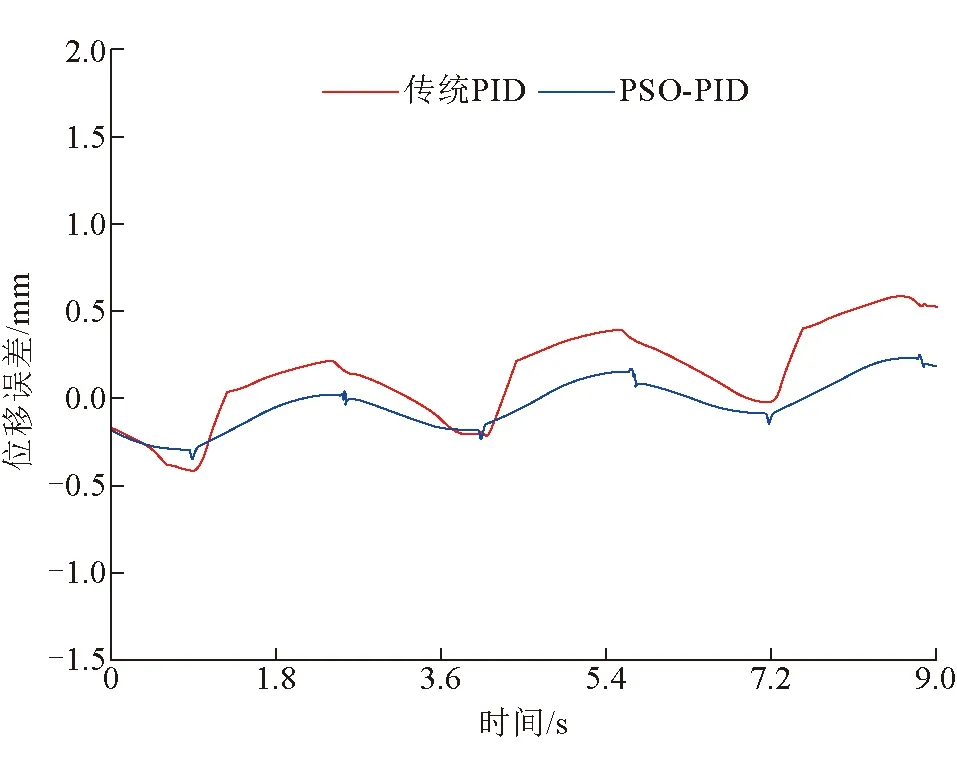
图12 基于RBF神经网络优化PID轨迹跟踪位移误差曲线

5 结论

针对煤矿安全生产中煤矿提升位置指示器等一些需要高精度位置控制的关键设备，设计研究了一套磁偶式无杆气缸非线性位置伺服控制系统。通过分析影响非线性位置伺服控制系统位置精确控制的影响因素，解析阀控缸系统气体的流动原理。建立了气动系统的质量流量方程、能量方程、压力微方程和动力学方程。然后将上述所有方程联立，构建成了磁偶式无杆气缸非线性位置伺服控制系统的数学模型，接着验证了气动系统数学模型的正确性与有效性。最后，又设计了基于RBF神经网络优化PID的控制器，并与传统PID控制结果进行了对比。结果表明：基于RBF神经网络优化PID参数控制策略的位置控制精度较高，运行的速度稳定性较好，有效提高了煤矿安全生产中关键设备运行的精确位置控制，增加了煤矿生产的安全性。

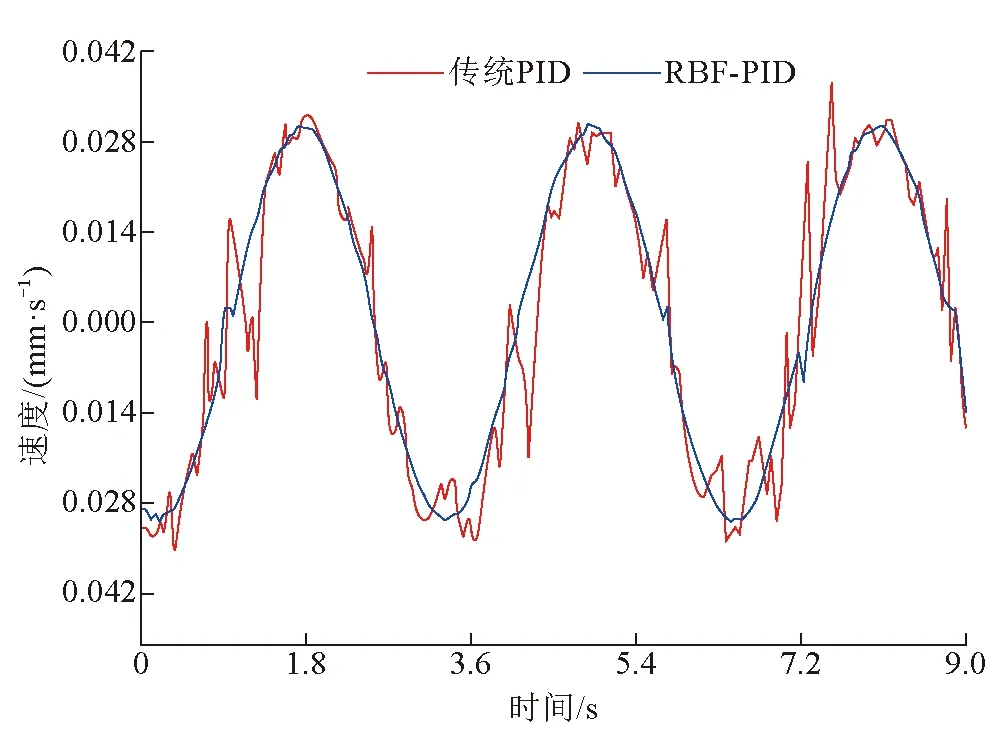
图13 基于RBF神经网络优化PID轨迹跟踪速度曲线