基于混合算法优化的BP-PID在SLS预热温度控制系统中的应用

张亚鹏，唐文秀，肖亚宁，裴玲艺，郭艳玲

（东北林业大学 机电工程学院，哈尔滨 150040）

0 引言

选择性激光烧结是一种近年来大跨步式发展的快速成型技术之一。其优点在于成型过程不需要支撑，能够缩短产品从设计到生产的开发周期，因而广泛应用于生物、航空、机械等多个领域[1]。在SLS的加工过程中，预热环节严重影响着成型件的质量和精度[2]。预热温度过低，成型件发生翘曲变形；预热温度过高，未进行激光扫描烧结的部分可能烧结成块，影响烧结件的后处理[3]。因此如何实现预热温度控制的准确性和稳定性等问题一直以来都是学者研究的热点。

由于加热装置的位置、散热环境、温度传感器信号的延时等因素影响，SLS的预热温度过程具有复杂非线性、大滞后和时变性[4]。传统PID控制器由于其参数是离线调节的，对复杂非线性对象的控制效果很差[5]。BP神经网络可以很好的克服系统参数变化和非线性等不确定因素的影响[6]，将BP神经网络与传统PID控制器相结合可以在一定范围内实现参数自适应调节，但BP算法存在收敛速度慢、收敛精度低、学习效率低等问题[7]，使得BP-PID响应时间长、控制效果差和控制精度低。为此，文献[8]利用离线的遗传算法对BP神经网络的初始权值进行优化；文献[9]利用LQR优化BP神经网络的输出以便满足实际的PID增益；文献[10]利用粒子群算法优化BP神经网络的初始权值。以上这些方法在不同程度上提高了BP-PID的控制效果，但其响应速度和控制精度仍具有提升空间。

基于此，本文提出采用混合算法优化的BP-PID控制方法（简称GA-BP-PSO的PID控制器）。利用MATLAB 2019a进行仿真，将本文提出的GA-BP-PSO的PID与传统PID和BP-PID进行对比，仿真结果表明本文提出的控制方法具有更快的响应速度、更高的控制精度以及更好的控制效果；将此控制器应用于实际预热温度控制，测试结果论证了该方法的有效性。

1 预热温度控制结构设计

加热装置是基于红外加热管的热辐射对材料粉末进行加热的。预热温度控制系统结构图如图1所示。首先，温度传感器采集烧结平面的材料粉末温度，其温度信号经过A/D转换传输至STM32单片机；其次，单片机收到的信号数据与目标值比较；最后，通过PID算法调节固态继电器的输出PWM波的占空比，从而调节红外加热管的功率，以此控制烧结平面温度。

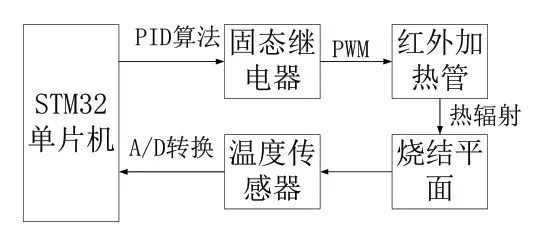
图1 温度控制系统结构图

2 基于GA-BP-PSO的PID控制器的设计

2.1 BP-PID控制器

BP-PID控制器是在PID控制器的基础上加入BP神经网络，其结构图如图2所示。PID控制器按照偏差的比例、积分、微分对系统进行控制。由于增量式PID控制算法可以减少累计误差[11]，提高控制精度，故本文采用增量式PID算法，即：

图2 BP-PID结构图

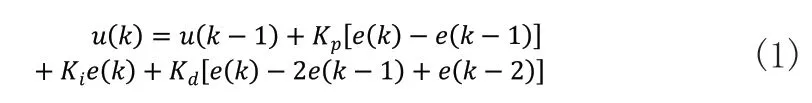
式(1)中，u(k)为控制器输出；Kp、Ki、Kd分别为比例、积分、微分系数；e(k)为系统期望输出值与实际输出值之间的差值。

BP神经网络结构图如图3所示。图中神经网络的输入x(i)信号取自系统的预热温度设定值r(k)、预热温度的实际y(k)值和误差e(k)。其中e(k)=r(k)-y(k)，故取输入层神经元个数为3；BP神经网络的输出信号分别为PID控制器的参数Kp、Ki、Kd，故取输出层神经元个数为3；BP神经网络隐含层神经元个数[12]：

图3 BP神经网络结构图

式(2)中，M为隐含层神经元个数；n为输入层神经元个数；l为输出层神经元个数；a为0～10的常数。

由式(2)可以选取隐含层神经元个数为5，将输入信号x(i)送往BP的隐含层，得到隐含层第j个神经元的输出Oin(j)：

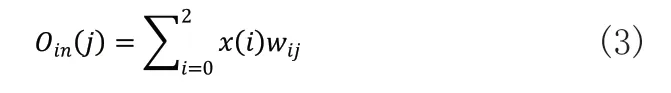
式(3)中，wij为输入层到隐含层之间的连接权值：

在输出层，得出第h个神经元的输入为yin(h)：

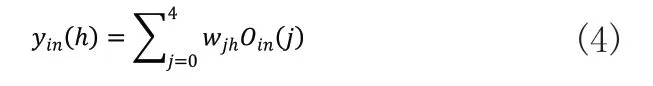
式(4)中，wjh为隐含层到输出层之间的连接权值Oout(h)。经过激励函数S(·)，得出第h个神经元的输出：

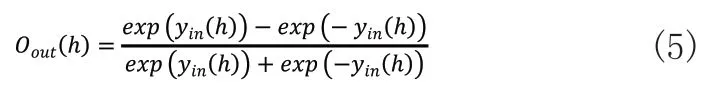
2.2 遗传算法

遗传算法是1960年 John holland提出的一种基于生物遗传机理，即生物进化(自然淘汰、交叉、变异等)现象的随机搜索算法，它通过计算机模拟生物进化过程进行搜索和进化，最后求出最优解[13]。BP神经网络的初始权值包括输入层到隐含层之间的权值和隐含层到输出层的权值，一般来说都是随机选取的，这导致BP神经网络学习过程的不稳定、低效率、时间漫长等问题[14]。因此，本文采用GA寻找最佳初始权值和阈值，从而提高BP神经网络学习的效率和稳定性。

本文中，输入层到隐含层权值wij个数为15个，隐含层到输出层权值wjh个数为15个，阈值包括隐含层阈值5个和输出层阈值3个。故将染色体的维数选为38，前30维每一维代表着权值；后8维每一维代表着阈值。

在个体寻优的过程中采用输出值和实际值的差的平方和作为适应度函数J：

式(6)中，h为输出层神经元个数；yi为BP神经网路中第个输出神经元的理论输出；oi为BP神经网路中第i个输出神经元的实际输出。

显然适应度值越小，个体越优。选择操作采用轮盘赌法，即适应度值越小的个体越容易被选中。经选中的个体以交叉概率进行下式的交叉操作：

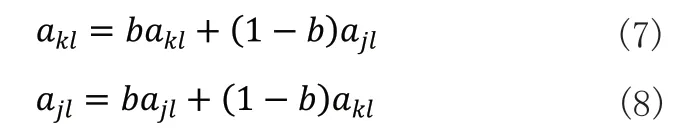
式(7)、式(8)中，akl和ajl表示第k个个体和第j个个体在第l维处进行交叉，b为[0,1]随机数。

变异采用的是以一个固定变异概率pc的随机发生变异的方法。

2.3 粒子群算法

粒子群算法是1995年Eberhart和Kennedy提出的一种元启发式算法，是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法[15]。BP的反向学习采用梯度下降法，但由于梯度下降法自身局限性，会使BP神经网络收敛慢、易陷入局部最小[16]。而粒子群优化算法避免了梯度下降法中对函数求导的过程，因此用粒子群算法代替BP 算法中的梯度下降法，可以提高BP神经网络的收敛速度并避免进入局部最小。

由2.2节可知，需要更新修改的权值和阈值个数为38个，故粒子向量维数为38，每一维代表着权值或阈值。在初始化粒子时，先初始化一个二维矩阵，该矩阵0到37列表示粒子位置，38到75列表示粒子速度，76列表示粒子适应度；为了方便计算，采取0～29列表示权值，30～37列表示阈值；每个粒子会根据由Kennedy和Eberhart提出的公式进行更新位置和速度[17]。

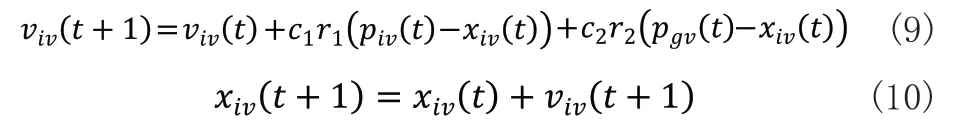
式(9)、式(10)中，c1和c2是学习因子；r1和r2是服从[0,1]上均匀分布的随机数；viv(t)∈[-vmax,vmax]，为第i个粒子的当前速度；xiv(t)∈[-xmax,xmax]，为第i个粒子的当前位置；piv(t)为第i个粒子到目前为止搜索到的个体最优位置；pgv(t)为整个粒子群到目前为止搜索到的整体最优位置。在更新过程中，若速度或位置超出最大值或最小值时，则令该速度或位置为最大值或最小值。

在粒子寻优过程中采用样本输出值和实际值的差的平方和作为适应度函数J：

式(11)中，n为训练样本数目；oij表示第i个粒子的第j个样本的理论输出值；yij表示第i个粒子的第j个样本的实际输出值。

2.4 GA-BP-PSO优化PID控制器的流程

GA-BP-PSO-PID的控制器结构图如图3所示。

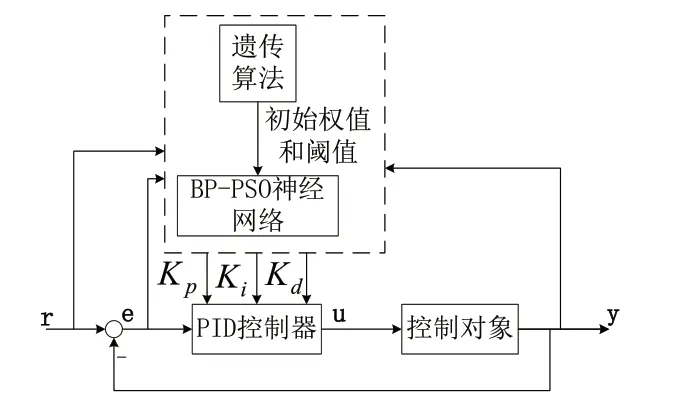
图4 GA-BP-PSO的PID控制器结构图

GA-BP-PSO的PID算法实现步骤如下：

Step1：遗传算法参数初始化，即进化迭代次数T，种群规模N，变异概率等，计算个体适应度；

Step2：根据轮盘赌法选择个体。被选中的个体通过以交叉概率通过式(7)和式(8)进行交叉操作，对整个种群以变异概率进行变异操作；

Step3：计算个体适应度，更新最优个体。判断是否满足遗传算法结束条件，若未满足，则跳转至Step2；若满足，则跳转至Step4；

Step4：输出最优个体，并将其赋值给BP神经网络的初始权值和阈值。

Step5：粒子群算法参数初始化，即迭代次数T，种群规模N，学习因子等，计算粒子适应度；

Step6：通过式(9)和式(10)更新粒子的速度和位置；

Step7：计算粒子适应度，更新当前最优值和全局最优值。判断是否满足粒子群算法结束条件，若未满足，则跳转至Step6；若满足，则跳转至Step8；

Step8：输出全局最优值，作为最终BP神经网络的权值和阈值。

3 仿真实验与分析

本文在MATLAB 2019a上进行仿真，设置GA算法的进化次数为50，种群规模为50，交叉概率为0.25，变异概率为0.1；PSO算法选取迭代次数为50，粒子种群规模为50，步长因子c1为2，步长因子c2为2，惯性因子ω取0.6；BP-PID的学习因子α为0.05，学习因子η为0.5；并根据实际经验给出传统PID的参数KP取4.023，Ki取2.105，Kd取13.305。GA算法优化BP神经网络的初始权值和阈值，得出最佳适应度和平均适应度随进化次数变化的曲线，如图5所示。PSO算法优化BP神经网络的反向学习，得出最佳适应度随进化次数变化的曲线，如图6所示。

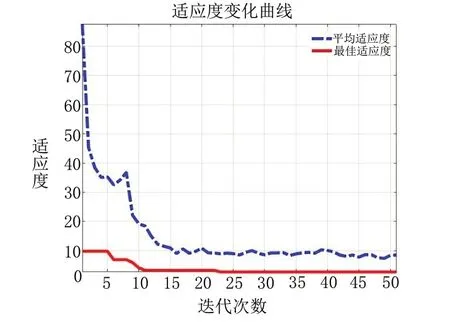
图5 适应度变化曲线图

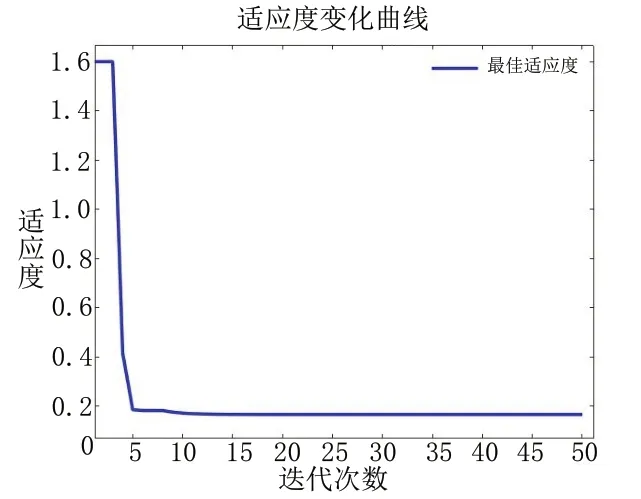
图6 适应度变化曲线图

为说明本文提出的GA-BP-PSO-PID控制器的控制效果，结合传统PID、BP-PID和GA-BP-PID，对其做出了阶跃响应曲线图和误差曲线图对比图以及本文所提控制方法的PID参数变化曲线图，如图7～图9所示。

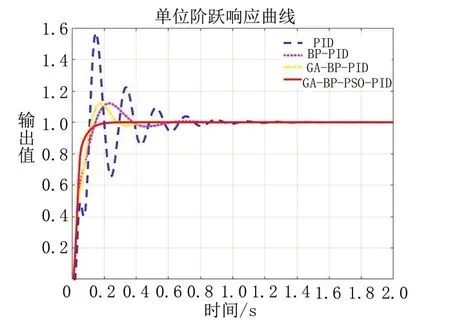
图7 阶跃响应曲线图

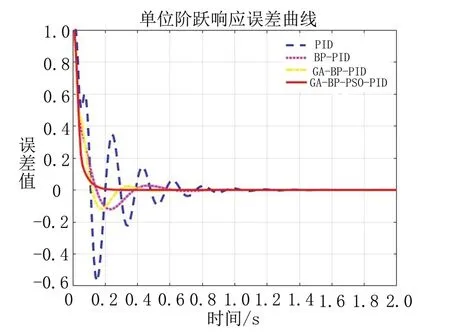
图8 误差变化曲线图

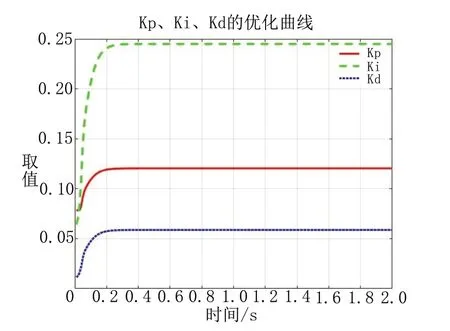
图9 PID参数的变化曲线图

由图7～图9可以看出，相较于传统PID、BP-PID和GA-BPPID，本文提出的GA-BP-PSO的PID控制方法达到了无振荡、无超调，具有更快的响应速度和更小的稳态误差；并且其PID参数变化较快，波动较小，验证了改进策略的有效性。

将这四种方法前2s的仿真结果进行处理得到各个控制器的控制性能指标对比，如表1所示。

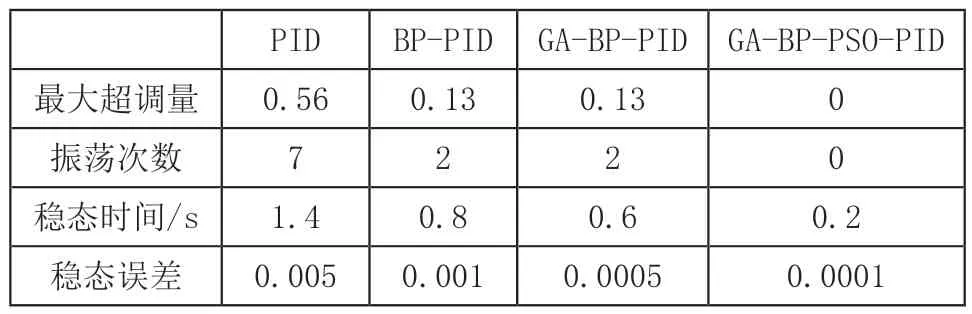
表1 性能指标对比

从表1可以看出，本文提出的GA-BP-PSO的PID控制方法相比于PID控制器，其稳态时间提前1.2s，稳态误差降低98%；相比于BP-PID控制器的稳态时间提前0.6s，稳态误差降低90%；相比于GA-BP-PID控制器的稳态时间提前0.4s，稳态误差降低80%。说明该控制器有效的提高了系统的响应速度和控制精度。

4 实验与应用

本实验是在基于自主设计研发的CX-B200快速成型机进行，其主要参数有成型尺寸：200mm200mm200mm、激光功率：40W的激光器、扫描速度：2000mm/s、分层厚度：0.08mm0.4mm，如图10所示。在本文中采用由四根规格相同的远红外加热管组成正方形加热装置，如图11所示。加热装置安置于烧结平面正上方，以便对需要烧结的材料进行预热和保温处理。加热装置和烧结平面的位置如图12所示。

图10 CX-A200激光烧结3D打印机

图11 加热装置

图12 加热装置和烧结平面的位置

将控制器用于预热温度控制系统中，材料粉末选为核桃壳复合粉末，根据文献[18]，得知该材料的最佳预热温度，设置预热温度目标值为80。由于烧结平面面积较大和热传递等问题，导致该平面每一处的温度都在波动变化，因此选取烧结平面中较为特殊的两个点，即烧结平面的中心点和角点，其中心点是烧结平面的原点；角点是所能烧结的最大范围的一个直角。在室内温度为15的情况下采用世敖SA-small系列的温度传感器和中泰联创PC6030数据采集卡收集了中心点和角点的温度随时间变化的数据，并用LABVIEW 2015画出了变化曲线，分别如图13和如图14示。

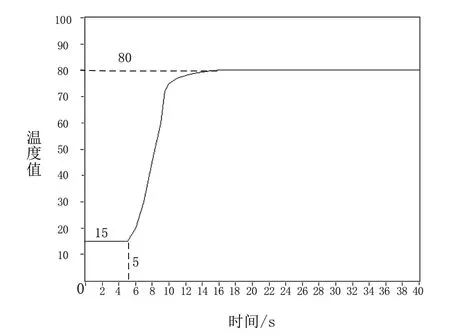
图13 中心点的温度变化曲线

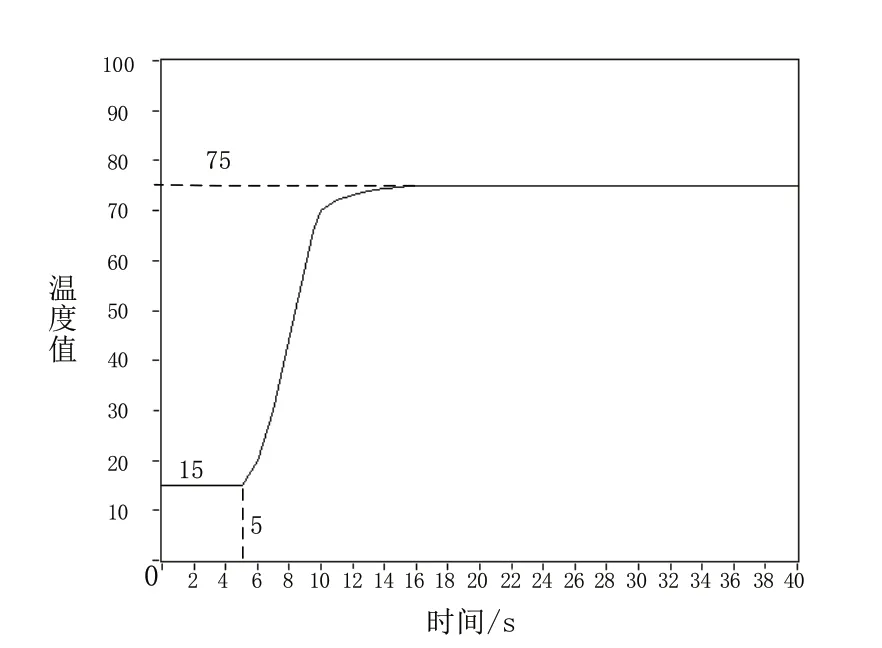
图14 角点温度变化曲线

从图13和图14中可以看出，开始时温度并没有变化，这是由于温度控制系统的延时环节引起的，而曲线在5秒开始变化，响应速度快、没有产生超调量且稳态误差小。在预热温度目标值为80时，中心点的温度稳定于约80，角点的温度稳定于约75，该烧结平面温度维持且稳定在75到80之间，整个烧结平面的温度差较小，表明该控制器对于预热温度有良好的控制效果。

5 结语

针对目前激光烧结预热温度的控制效果差、控制精度低和预热时间长等问题，本文提出了混合算法优化的BPPID控制方法，将该控制器应用于选择性激光烧结预热温度的控制中。从仿真和实验结果可以看出，相比PID和BPPID，GA-BP-PSO的PID控制器有更快的响应速度且不存在振荡，预热温度更加稳定和准确，提高了预热温度的控制效果，从而有助于改善烧结件的质量和精度。