基于响应面法的轴向混合励磁双凸极航空发电机优化设计

马昕晨，陈志辉，赵雅周

1.南京航空航天大学，江苏 南京 210016

2.北京曙光航空电气有限责任公司，北京 100020

在270Ⅴ高压直流电源系统中，双凸极电机由于具有结构简单坚固、使用安全、适用于高速运行等优点，逐渐成为飞机的起动/发电机首选的电机种类之一，近年来也逐渐受到国内外电机领域学者的广泛关注和研究[1]。双凸极电机包括开关磁阻电机、永磁双凸极电机、电励磁双凸极电机和混合励磁双凸极电机。其中，混合励磁双凸极电机结合了永磁双凸极电机和电励磁双凸极电机的优点，既有永磁励磁可供独立发电，又有电励磁扩大调节气隙磁场范围，功率密度高，控制简单，容错性高，在航空航天、电动汽车、风力发电等领域都具有潜在的应用前景[2]。

混合励磁双凸极电机同时采用永磁励磁与电励磁，电机结构相对复杂，因此如何优化电机结构以获取更高的功率密度和效率是电机设计过程中需要解决的问题之一。参考文献[3]针对新型双转子混合励磁电机，建立电机有限元求解模型，通过分析电机内的电磁场，得出最优结构及参数；参考文献[4]选取电机转矩、效率作为目标函数，定转子极弧、永磁体尺寸4个变量为优化变量，使用多目标量子进化算法，对混合励磁开关磁阻电机进行多目标优化设计；参考文献[5]针对混合励磁双定子磁悬浮开关磁阻电机，以平均转矩/体积比与平均悬浮力/体积比作为优化目标，通过单变量分析法研究结构参数对优化目标的影响，将影响优化目标的主要参数作为优化参数，再采样遗传算法寻优。

本文对一台新型轴向混合励磁双凸极发电机（AHEDSM）进行优化设计和分析，以提高电机输出功率为目的，将磁链作为电机优化目标，通过分析电机数学模型，将对磁链有影响的结构参数作为初始优化参数，采用田口正交试验设计筛选出对磁链影响最大的关键结构尺寸参数，响应面法建立电机优化模型，再与自适应遗传算法相结合获得最佳变量优化组合，最后用有限元法验证所得结果的正确性[6-7]。

1 电机结构设计

图1 为AHEDSM 电机结构，包含双定子铁芯、双转子铁芯、内外导磁体、永磁体、直流励磁绕组、电枢绕组等部件。电机为12/8极，三相，定转子铁芯均为凸极结构。定子铁芯分为上下两段，沿轴对称放置，每段定子铁芯等分为4份，每份包含三个定子齿，分别嵌放A、B、C各相集中绕组。在上下两侧定子齿上，每相对应的4个绕组串联，形成三相绕组；上下转子同样沿轴放置，并相互错开22.5°，转子上无绕组。励磁绕组为集中式环形绕组，放置于双转子铁芯之间。定子外侧导磁体同样等分为4 份，永磁体放置在相对的两片外导磁体中央。该瓦片状永磁体为轴向磁化，且两片永磁体磁化方向一致。

影响电机性能的主要参数为机壳外径D、电机总长H、每段铁芯长度he、永磁体厚度hm、气隙直径Dδ、定子外径Ds、转子内径Dr、轴直径Da、内导磁体直径Dn、定子轭高h1i和转子轭高h2i等，如图2所示。

AHEDSM 作为高压直流发电机，需外接整流器，输出直流电能。图3给出了二极管不控三相桥整流电路拓扑。其中，ua、ub、uc分别为PWM 三相输入电压，ia、ib、ic分别为AHEDSM 三相输出电流，Ro为直流侧等效负载，Uo为输出直流电压，输出端无滤波电容。

根据电机设计经验，取电机气隙为0.5mm，槽满率为70%，励磁绕组线径为1.725mm，电枢绕组线径为3.665mm；励磁绕组环绕内导磁体，置于双转子之间，且与上下转子均需留有6.5mm的间隙，与内导磁体留有4mm的间隙，用于放置励磁绕组支架且防止转子高速转动时摩擦励磁绕组；励磁绕组与定子内径之间需留有1mm 的间隙，防止与电枢绕组接触；则励磁绕组槽面积为

同理，根据定子外径Ds、定子轭高h1i、气隙直径Dδ可计算定子槽面积Sa，一个槽内放置两个电枢绕组线圈，则电枢绕组匝数为

电枢绕组匝数越大，电机电感越大，高速运行时感抗越大，功率因数越低，故Na应不大于15 匝。电机设计指标为设计额定转速12000r/min，额定直流电压270Ⅴ，额定功率5kW。根据电磁校核计算和结构参数的调整，电机初始尺寸参数见表1。

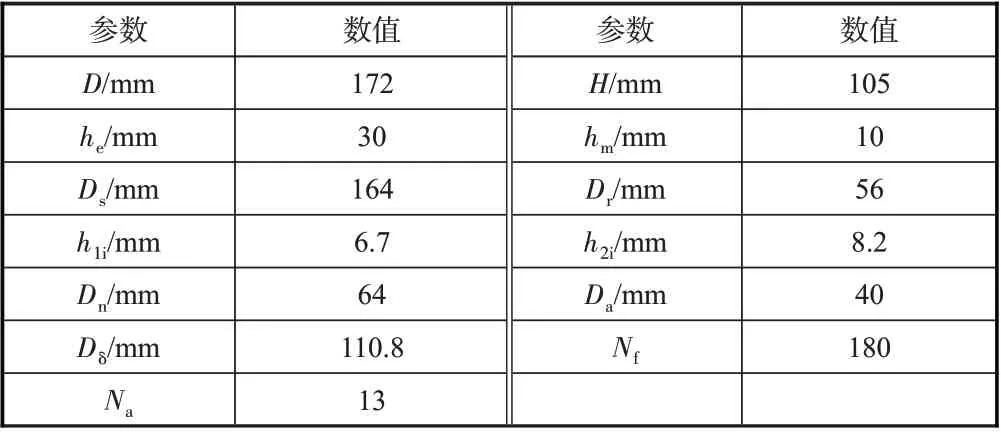
表1 AHEDSM结构尺寸Table 1 Structure parameters of AHEDSM

2 优化设计

2.1 优化总流程

本文根据初始设计参数，在ANSYS仿真软件中搭建其三维有限元模型。由于AHEDSM具有特殊的双定子、双转子结构，结构复杂，优化过程中需要考虑的尺寸参数众多，为了兼顾全面优化电机和提高优化效率，先根据电机工作原理分析需要优化的尺寸参数，再建立田口正交试验表确定各参数对目标函数的影响率，选取影响率大的参数作为后续优化的关键结构尺寸参数。采用中心复合设计试验得到数据点，搭建响应面模型，结合自适应遗传算法求取响应面函数的最优值点，经有限元仿真验证，确定最终的尺寸参数。优化流程如图4所示。

2.2 优化变量及目标

发电机优化的目的为在输入功率不变的情况下，合理设置计算电机电磁参数，使电机输出电压最大。电机电枢各相绕组匝链的磁链大小决定着电机输出功率的大小，根据电机工作原理，各相绕组匝链的磁链越大，反电动势越大，经整流后输出电压越大，从而输出功率增大，所以将电机单相绕组匝链的磁链幅值作为优化目标。

优化过程中，应尽量保持电机体积不变，则将机壳外径D、电机总长H、轴直径Da、内导磁体直径Dn、转子内径Dr设置为定值。

根据电机的工作原理，电机磁链为

式中，永磁体磁势Fm与永磁体厚度hm有关，励磁磁势Ff与励磁绕组匝数Nf有关，永磁体磁阻Rm为永磁体厚度hm和定子外径Ds的函数，气隙磁阻Rδ为气隙直径Dδ和每段铁芯长度he的函数，由式（3）得到电枢绕组匝数Na与定子轭高h1i有关；综上，将hm、Ds、Dδ、he及h1i设为优化变量。每个优化变量分别有4个水平变量，取值见表2。

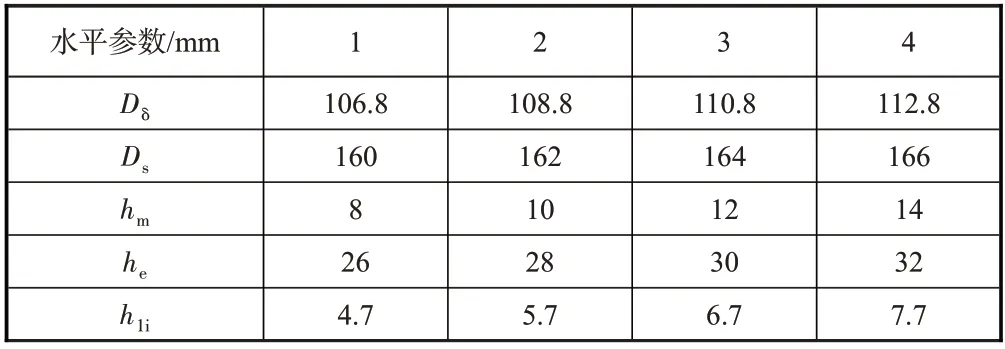
表2 优化参数及参数变量取值Table 2 Optimization parameters and parameter values of the variables

根据田口法设计L9(45)正交表并建立试验矩阵[6-7]，绕组匝数随电机尺寸变化而变化，取励磁电流为12A，利用有限元分析得到磁链最大值，见表3。

根据表3中结果，计算各优化参数的平均值和方差，得到各参数变化对磁链影响所占的比重。x为不同的优化参数，i为1、2、3、4的4个水平，则不同优化参数每个水平下的平均值为

计算结果见表4。取每个参数4个平均值中的最大值，则使磁链最大的参数组合见表5。

表4 各优化参数各水平下的平均值Table 4 Average value of optimization parameters at each level

表5 最优参数组合Table 5 Optimal parameters combination

根据表3，得磁链平均值为

表3 正交表及试验结果Table 3 Orthogonal table and test results

式中，n为试验次数。各优化参数的方差计算公式为

得到每个参数的影响比重，见表6。根据表6 中的结果，初选的5个参数中对磁链影响较大的为气隙直径Dδ、定子外径Ds和定子轭高h1i，所占比重分别为29.38%、18.91%和45.10%，故将这三个参数作为后续优化的优化参数，初值见表5；永磁体厚度hm和每段铁芯长度he对磁链影响较小，故设为定值，取值见表5。

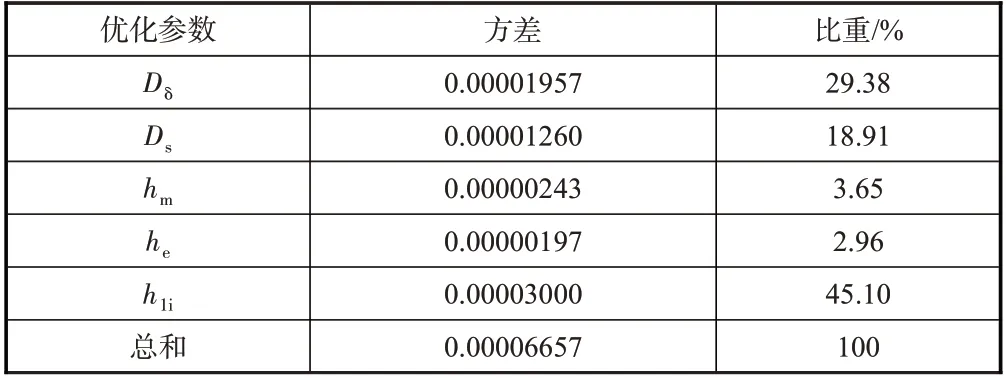
表6 优化参数对磁链的影响比重Table 6 Influence proportion of optimization parameters on the flux linkage

2.3 响应面模型建立

响应面法（RSM）通过对指定设计空间内的样本点的集合进行有限的试验设计（DOE），选择出具有代表性的局部各点进行试验，拟合全局范围内变量与目标间的函数关系来代替真实响应面[8]。

试验设计方法主要分为经典采样和全空间分布型采样[9-10]两大类。经典采样包括部分因子试验（FFD）、全因子试验（FFD）、中心复合试验（CCD）和Box-Behnken 方法等；全空间分布型采样主要有正交设计（OD）和拉丁超立方设计（LSD）等。全因子/部分因子试验耗时长，LSD对样本采样要求较高，综合考虑，本文采用CCD进行试验设计。

本文选用CCD 设计中应用最广的表面集中型中心复合试验（CCF）设计，每个变量仅需三个水平，设计复杂性降低。优化变量为气隙直径Dδ、定子外径Ds和定子轭高h1i，每个变量具有-1、0、1三个水平，-1是变量取值范围的最小值，0 是变量取值范围的平均值，1 是变量取值范围的最大值。变量取值见表7。

表7 优化变量水平设计Table 7 Optimizing variable level design

借助ANSYS三维仿真软件得到每组样本点的响应值，电枢绕组匝数同样随着电机尺寸的变化而变化，表8 是设计试验样本点及其对应的磁链响应值。

表8 CCF采样表Table 8 CCF sampling sheet

由于优化变量X与目标Y之间复杂的非线性关系，无法写出明确的函数表达式，因此只能用响应面模型构造近似函数来逼近真实函数[11]。构建响应面模型的方法包括多项式回归法、人工神经网络法、kriging 函数法和径向基函数法；由于人工神经网络法和kriging 函数拟合所需时间较长，径向基函数适用于曲面重构，多项式回归法适用于少变量低阶问题，精度高且收敛速度快，因此本文综合考虑，选用多项式回归方法进行响应面建模。为了得到更加精确的弯曲响应，选用三元二阶响应面函数，其表达式如下

式中，β0、βi、βii、βij为待估算的回归系数；ε为拟合误差；xi、xj为变量。

用矩阵表示为

式中，n为样本点数；m为自变量的数目；yˉ为试验平均值；yi为第i个样本点的试验值；ŷi为第i个样本点的预测值；SSE为残差平方和；SST为总偏差平方和。计算公式如下

该响应面模型的检验系数见表9，拟合程度较好，可用于后续优化中。

表9 响应面模型的拟合程度Table 9 Fitting degree of response surface model

2.4 自适应遗传算法优化

自适应遗传算法是一种简化的模拟生物遗传和变异过程的算法，基本原理是随机产生一组解，经过数字编码成为染色体，得到初始种群；计算种群中各个个体的适应度，按照适者生存和优胜劣汰的原理，淘汰适应度值低的个体，选择适应度值高的个体进行交叉、变异，产生新一代种群，并对新的种群继续进行更新换代，直到找到最优解[12-15]。遗传算法的具体流程如图5所示。

选取响应面的三个设计参数为优化变量，调用Matlab遗传算法函数进行多目标优化，算法默认求解的是最小值，而目标是磁链最大，因此优化目标为磁链的倒数，适应度函数为响应面模型的倒数，具体问题归结为

优化结果见表10。至此，优化过程全部结束。

表10 遗传算法的分析结果Table 10 Analysis results of genetic algorithm

3 优化结果验证

利用ANSYS 有限元分析软件对上文所求解出的最优设计进行仿真验证，比较优化前后电机电磁性能的差异见表11。

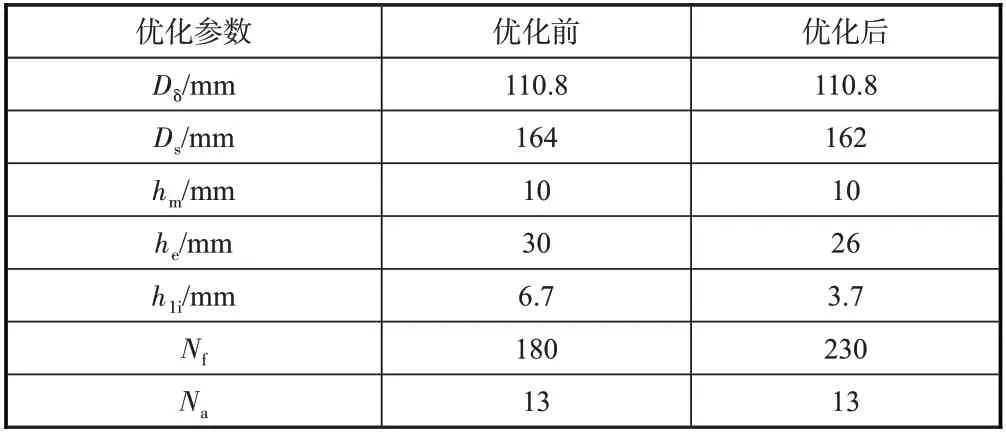
表11 优化前后参数对比Table 11 Comparison between parameters before and after optimization

图6 为电机优化前后磁链波形，A、B、C 三相的磁链波形互差120°电角度，优化前的电机磁链幅值为0.0230Wb，优化后的磁链幅值为0.0245Wb，提高了6.5%。

电机空载反电势的波形如图7 所示，优化前电机空载反电势的有效值为161.47Ⅴ，优化后电机空载反电势的有效值为171.20Ⅴ，增长了6.0%。

电机尺寸的改变同样会引起齿槽转矩的变化，如图8所示。虽然优化后的电机的电磁性能有所改善，但齿槽转矩也有所增加，峰峰值由原来的0.458N·m 增大到0.529N·m。

4 结论

本文针对AHEDSM 电机双定子、双转子的复杂结构，提出一种基本响应面模型的多参数优化方法。根据田口正交表分析参数对目标的影响比重，筛选出对电机磁链影响最大的关键结构尺寸参数，采用中心复合设计试验得到数据点，搭建响应面模型，结合自适应遗传算法，快速有效地确定电机最优结构尺寸参数。通过ANSYS 有限元分析软件计算电机的磁链及空载反电势，表明经优化调整后，电机的电磁性能有了明显改善，从而验证了该理论分析和优化方法的正确性。