基于修正双梁理论的邮轮应力分布特性研究

杨 斌，裴志勇，吴卫国

（武汉理工大学a.交通学院；b.船舶邮轮中心，武汉 430063）

0 引 言

大型邮轮丰满上层建筑带来巨大经济效益的同时，也对船体结构与强度设计提出了更高的要求。在邮轮设计初期一般使用简单梁理论估算结构的应力水平，当大型邮轮发生中拱或中垂弯曲时，由于邮轮主船体和上层建筑结构的复杂性，力并不能完全有效地向上传递，因此剖面内的纵向应力不再沿高度方向保持线性分布[1]。其次相较于一般船舶，邮轮上层建筑拥有较多的侧壁开口和甲板开口，导致其剪切刚度降低，上层建筑舷侧以及纵舱壁等构件在传递纵向应力的同时还需承受较大的剪切应力。无论是力的垂向传递还是剪切应力的增加，都会使得邮轮船体结构的受力变形更加复杂。

1950 年，Crawford[2]提出“双梁理论”，将主船体和上层建筑分别视为两根独立的梁，基于简单梁理论，对上层建筑的弯曲变形进行了研究探讨。随后许多学者对此理论做出了研究和拓展。裴志勇等[3]应用双梁理论来模拟散货船隔舱重载下局部弯曲引起的应力分布，研究双层底结构的局部弯曲应力对船体梁极限强度的影响。陈倩等[4]应用有限元方法对铝合金上层建筑参与船体总纵弯曲的特性进行计算分析，得到了铝合金上层建筑与主船体之间的应力分布及总纵弯曲应力在船舯剖面上的分布，并与钢质上层建筑的计算结果进行了比较。

Bleich[5]对上层建筑纵向应力进行了直接计算，对上层建筑与主船体弯曲曲率不一致的现象做了详细讨论。Naar 等[6]将Bleich 提出的梁理论拓展到了多层上层建筑，提出耦合梁理论，该理论假定邮轮由多个梁组成，每个梁之间由纵向和垂向分布的弹簧进行耦合，来估算邮轮上层建筑的纵向应力。Morshedsolouk等[7]提出了耦合梁理论的拓展公式，用于研究拥有多层上层建筑客船的纵向应力沿高度分布特性。

Pei等[8]在双梁理论的基础上，分析了邮轮主船体和上层建筑之间的相互作用，对上层建筑的弯曲效率进行了研究和讨论，为邮轮上层建筑的结构设计提供了技术支持。朱波[1]从上层建筑结构形式的角度，通过理论分析与数值仿真相结合的方式，系统地探讨上层建筑长度和宽度等因素对邮轮上层建筑有效度的影响。Zou[9]以内河邮轮为研究对象，探讨并分析了上层建筑的弯曲效率对船体梁强度的贡献程度。Romanoff 等[10]研究了在弯曲荷载作用下，客船主船体与上层建筑之间的相互作用，并考虑到各甲板之间的刚度变化。

传统双梁理论是在梁理论基础上进行推导，并基于一定假设条件下进行应用。在对邮轮纵向应力沿高度分布特性研究时，需要对双梁理论进行一定修正，以满足邮轮多层上层建筑、上层建筑和主船体刚度存在差异等结构要求。耦合梁理论没有考虑横舱壁、横向强框架和上层建筑端部刚度等因素的影响，横向强框架处的剪切应力分布也不同于整船有限元计算结果。

本文首先探讨邮轮主船体和上层建筑之间的相互作用，其次假定邮轮主甲板上的竖向力迫使上层建筑产生与主船体产生相同曲率的挠度变形，使剖面发生歪斜的水平剪力产生不同曲率的剪切变形，并详述了修正后的双梁理论是如何考虑总纵弯曲下的挠度变形及剪切变形；考虑主船体和上层建筑之间的力传递会受到剪切滞后的影响，需要使用剪切滞后系数r对上层建筑所受弯矩M1进行修正；最后以一艘典型内河邮轮为研究对象，分别使用简单梁理论、双梁理论及本文提出的双梁理论修正方法计算了邮轮主船体和上层建筑的纵向应力，并与有限元法计算结果进行了对比分析。本文提出的双梁理论修正方法考虑了邮轮主船体和上层建筑之间的相互作用，适用于在邮轮设计初期，对客船、邮轮等拥有多层上层建筑的大型船舶的纵向应力估算。

1 邮轮上层建筑的变形特性

主船体最上层连续甲板以上的舱室结构物统称为上层建筑[11]。当上层建筑搁置在主船体上，若主船体发生总纵弯曲，上层建筑仍保持原状，于是两部分原来在同一竖直平面内的剖面将发生纵向移动和分离，如图1（a）所示。而实际情况是主船体和上层建筑之间是相互作用的，当主船体发生总纵弯曲时，在主船体与上层建筑连接线处会产生相互作用的水平剪力阻止剖面的纵向移动，以及相互作用的竖向力阻止剖面的竖向分离，如图1（b）所示。

如图2 所示，Q1、Q2为连接线上产生的相互作用的水平剪力[13]，单位是N。由于水平剪力的作用，会使主船体和上层建筑同一竖向剖面发生歪斜，并且越接近船舶首尾自由端，剖面的竖向分离越严重，因此产生的竖向力也越大，这种相互作用称为端点效应。

由首尾自由端产生的端点效应，主要表现在上层建筑长度中点剖面上的弯曲应力受上层建筑长度变化的影响，如图3 所示。对于短上层建筑，长度中点剖面离首尾两端较近，理论弯曲应力将大于受端点效应影响的实际弯曲应力值；对于长上层建筑，因为其长度中点剖面离首尾两端较远，受端点效应的影响较小，实际弯曲应力近似等于理论弯曲应力。

由于邮轮上层建筑几乎与主船体等长，属于长上层建筑，根据图3所示，在邮轮上层建筑中点剖面处的总纵应力应近似等于理论弯曲应力。由于自由端的端点效应导致的应力变化可忽略不计，因此本文选择邮轮上层建筑中点剖面作为研究对象，分析邮轮纵向应力沿高度分布特性。

邮轮上层建筑的变形特性需考虑到剪切滞后的影响。剪切滞后效应在结构工程中是一个普遍存在的力学现象，从力学本质上说，是圣维南原理，具体表现是在某一局部范围内，剪力所能起的作用有限，所以正应力分布不均匀，把这种正应力分布不均匀的现象叫做剪切滞后[15]。

由于主船体和上层建筑之间的刚度存在差异以及剪切滞后的影响，主船体和上层建筑在主甲板处计算得到的纵向应力并不一致，为了考虑剪切滞后的影响，引入剪切滞后系数r[12]，主船体与上层建筑相接处的纵向应力比，与上层建筑的长度l和宽度b有关。表达式如式（1）所示。

2 双梁理论及修正思想

2.1 双梁理论

由于船舶主船体与上层建筑之间的刚度差异，在船舶结构与强度设计中需考虑主船体与上层建筑的相互作用。双梁理论的核心思想是将主船体与上层建筑看作两根独立的梁，它们之间受到竖向力和水平剪力的相互作用，假设主船体受到外力作用的情况下，通过梁理论、能量法以及变分法等计算得到上层建筑与主船体的应力分布。

取船舶模型如图4 所示，设上层建筑为梁1，长度为l，主船体为梁2，长度为L；上层建筑中和轴距主甲板距离为aa1，主船体中和轴距主甲板距离为aa2，上层建筑中和轴和主船体中和轴距离为a；y1和y2为上层建筑和主船体由于外力作用产生的挠度变形。

双梁模型受力分析如图5 所示，上层建筑和主船体相互连接，连接线处的水平剪力和竖向力可相互传递。上层建筑力平衡方程为

主船体力平衡方程为

式中：N1、N2分别为上层建筑和主船体所受轴向力；M1、M2分别为上层建筑和主船体所受弯矩；A1、A2分别为上层建筑和主船体断面的横截面积；I1、I2分别为上层建筑和主船体对其本身中和轴的剖面惯性矩。

如图5 所示，由于外载荷的作用，上层建筑和主船体会产生轴向拉（压）和弯曲变形。

上层建筑正应力表达式为

主船体正应力表达式为

式中，y1、y2分别为所求截面上的应力点到上层建筑和主船体中性轴的距离。

利用“势能理论”，可以获得关于挠度变形y1和y2的微分方程，外力总势能UW=UP+US+UM，其中UP、US、UM是由外载荷P、剪力S和弯矩M产生的势能。

总应变能V=V1a+V1b+V1c+V2a+V2b+V2c+Vd，其中V1a、V2a是上层建筑和主船体轴向拉伸（压缩）产生的应变能；V1b、V2b是上层建筑和主船体由于弯曲产生的应变能；V1c、V2c是上层建筑和主船体由于垂直剪切力产生的应变能；除了纵向应力的应变能外，舱壁或甲板梁也会储存能量，以抵抗上层建筑和船体的相对垂直位移，这部分应变能可以表示为弹簧常数K的形式，符号是Vd。

至此，在得到总势能U=V+UW后，利用变分法原理求解δU=0，得到两个微分方程，通过变分法确定微分方程通解中出现的任意常数所需要的边界条件。联立微分方程组进行求解，得到上层建筑和主船体的挠度变形y1和y2，进而得到上层建筑和主船体沿高度方向的纵向正应力。

2.2 修正双梁理论

传统双梁理论是在梁理论基础上进行推导，并基于一定假设条件下应用。但由于方程数量过多和计算难度大等特点，很难在短时间内获得一个准确可靠的计算结果。

本文认为双梁连接线上的竖向力迫使上层建筑产生与主船体产生相同曲率的弯曲变形，水平剪力使剖面发生歪斜，上层建筑与主船体产生不同曲率的剪切变形；基于梁理论，对弯曲及剪切变形产生的应力进行了理论推导；考虑双梁连接线处剪切滞后的原因，使用剪切滞后系数r对上层建筑所受弯矩M1进行修正。

设上层建筑为梁1，主船体为梁2，双梁模型中和轴位置如图6 所示。图中h1、h2为上层建筑和主船体的高度，单位是cm；e1、e2分别为上层建筑和主船体中和轴到主甲板的距离，单位是cm；e0为双梁模型的中和轴高度，单位是cm。

中拱弯曲下双梁模型连接线处受力示意如图7所示。P1、P2为连接线上产生的相互作用的水平剪力，γ1、γ2表示由于剪切力Q1、Q2引起的剪切应变。P1、P2和Q1、Q2的关系如式（6）所示：

当梁的高度远小于跨度时，梁理论一般会忽略横向剪切变形的影响，但由于大型邮轮多层上层建筑的结构特点，致使横向剪切变形的影响变得不可忽略。梁由于剪切变形导致的剖面歪斜如图8（b）所示，此时横向剪切力Q所产生的剪切变形会将引起梁的附加挠度，并导致原来垂直于中面的剖面发生歪斜。γ表示由于剪切力Q引起的剪切应变，梁理论一般会忽略横向剪切变形的影响，γ为0，即截面的转动等于挠度曲线切线的斜率，从而保证符合平断面假定，如图8（a）所示，表示为

式中，dw/dx表示挠度曲线切线的斜率，θ表示由于弯曲变形引起的截面转动。

定义梁的变形曲率为ξ，考虑剪切变形的影响后，如图8（b）所示，ξ可表示为

假设双梁模型在外力作用下变形为纯弯曲，模型长度中点剖面受力示意图如图9所示。

图中M为模型所受外力，单位是N·cm；M1、M2分别为上层建筑和主船体弯矩，单位是N·cm；N1、N2分别为弯矩M引起的上层建筑和主船体的轴向力（中和轴处），大小相等，方向相反，单位是N；l为上层建筑长度，单位是cm；L为主船体长度，单位是cm。

梁1（上层建筑）纵向应力表达式为

梁2（主船体）纵向应力表达式为

式中：σ1、σ2分别为上层建筑和主船体的纵向应力，单位是N/cm2；I1、I2分别为上层建筑和主船体对其本身中和轴的剖面惯性矩，单位是cm4；y1、y2分别为上层建筑和主船体剖面位置至本身中和轴的距离，单位是cm；F1、F2分别为上层建筑和主船体的横剖面面积，单位是cm2。

假定双梁连接线上的竖向力迫使上层建筑产生与主船体产生相同曲率的挠度变形，这一部分的挠度曲线切线斜率用符号ν″1、ν″2表示。由于水平剪力的作用，使剖面发生歪斜，这一部分的剪切变形用符号γ1、γ2表示，因此梁1和梁2的总变形如式（11）所示：

式中：φ1、φ2分别为上层建筑和主船体弯曲后的总变形；γ1、γ2分别为主船体和上层建筑由剪切变形引起的剪切应变，γ1=-Q/A1G，γ2=Q/A2G。

截面的内力表达式为

双梁模型中和轴处的轴向力表达式为

式中，h2为主船体高度，单位是cm；εe1、εe2分别为水平剪切力Q引起的上层建筑和主船体在中和轴处的轴向应变，关系如图9所示。

双梁模型弯矩平衡方程式为

式中，e=e1+e2。

假设主船体与上层建筑之间相互作用的竖向力P和连线处的垂向变形成正比，比例设为垂向刚性系数K，如式（21）所示：

邮轮上层建筑几乎与主船体等长，其长度中点距端部较远，产生的竖向力较小，可忽略不计。因此可假设在长度中点处上层建筑和主船体的挠度变形一致，由此可得在长度中点处==ν″。

假设E=E1=E2，在主船体与上层建筑连线处纵向应力应存在以下关系：

式中，ε01、ε02为主船体和上层建筑连接线处的轴向应变。

联立上式可得

可求得水平剪切力Q为

至此，水平剪切力Q、剪切应变γ、挠度变形引起的曲率ν″都已得到，进而可以求得主船体和上层建筑所受弯矩M1、M2，由于连接线处剪切滞后的原因，需要对上层建筑所受弯矩M1进行修正。

主船体沿高度方向的纵向应力分布表达式为

根据式（24）可得主船体与上层建筑相接处主甲板的纵向应力σ02为

式中，y02为主甲板距主船体中和轴的距离，即y02=e2，ε02为主甲板处轴向应变，如图9所示，主甲板处轴向应变为0。由主船体与上层建筑相接处主甲板的纵向应力σ02反推上层建筑所受弯矩M1为

式中，y01=e1，表示主甲板距上层建筑中和轴的距离，单位是cm。上层建筑沿高度方向的纵向应力分布表达式为

式中，y1'表示所求剖面位置距主甲板距离，单位是cm。

3 邮轮纵向应力计算

本文以一艘典型内河邮轮为研究对象，计算分析该邮轮在中纵弯曲载荷下，船舯剖面沿高度方向分布的剖面纵向应力。该邮轮为双层底、单壳结构形式，每层甲板之间主要以支柱结构和横舱壁进行支撑连接。在船舶平行中体首尾处设有上下连续的横舱壁。全船采用钢质结构，船体主要尺度参数如表1所示，船体内各层甲板高度如表2所示，上层建筑及主船体参数如表3所示。

表1 邮轮主要尺度参数Tab.1 Main scale parameters of cruise ship

表2 邮轮甲板高度Tab.2 Cruise ship deck height

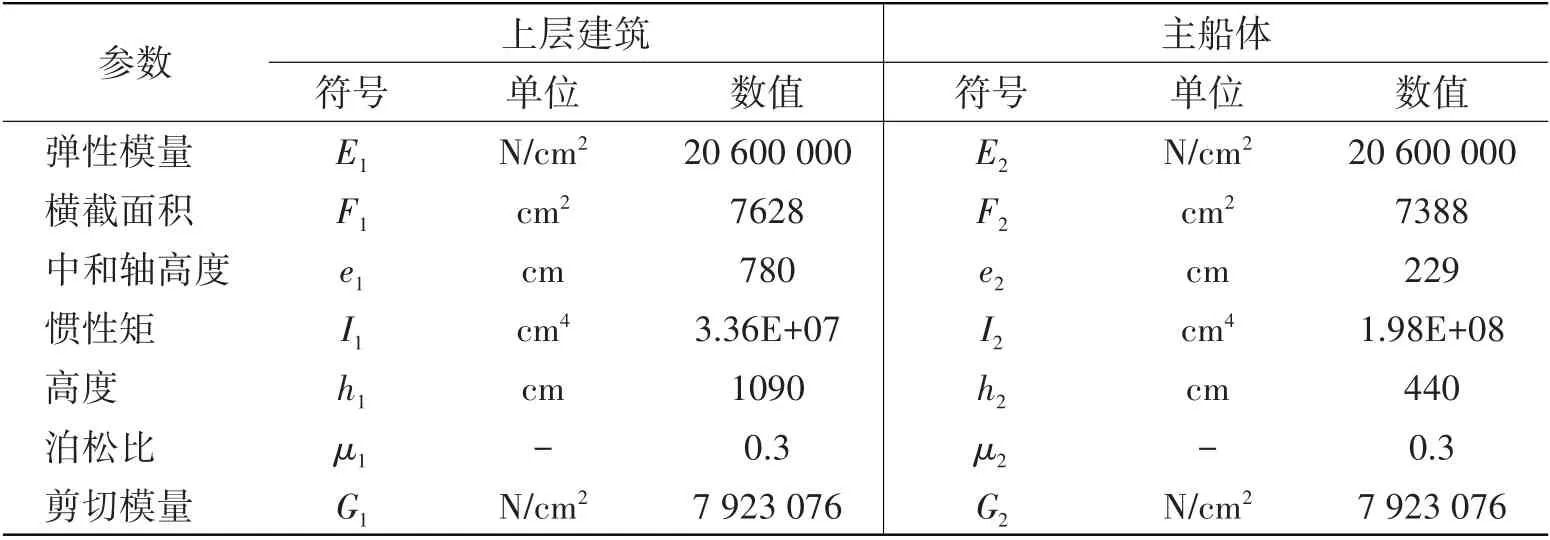
表3 上层建筑及主船体参数Tab.3 Superstructure and main hull parameters

本文基于一艘典型内河邮轮建立整船理想有限元模型[1]，通过刚性节点对模型两端进行约束，在船尾端节点处施加位移和扭转约束，在船首端施加通过英国劳氏规范《Rules and Regulations for the Classification of Naval Ships》（2008）[14]计算得到的弯矩载荷，大小为1.7×108N·m，对整船在中纵弯曲载荷下的结构响应进行计算分析。整船有限元模型如图11 所示，全船板单元网格大小平均在250×250 mm，板单元及梁单元共计约75万个。

为了减小端点效应的影响，选取船舯剖面作为研究对象，以弯曲应力为横坐标，邮轮高度为纵坐标，绘制纵向应力沿高度分布曲线，如图12所示。

梁理论、修正双梁理论与FEM计算结果如表4所示。

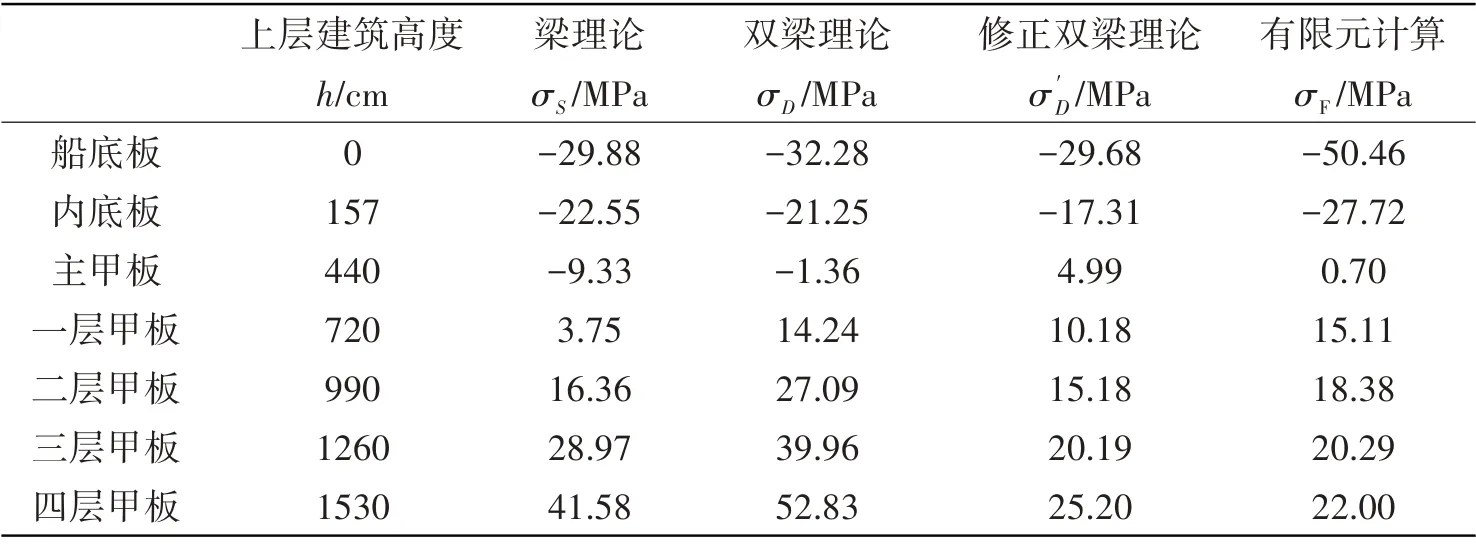
表4 梁理论、修正双梁理论与FEM计算结果Tab.4 Calculation results by beam theory,modified two-beam theory and FEM

表中，σS表示梁理论计算纵向应力，σD表示双梁理论计算纵向应力，σ'D表示修正双梁理论计算纵向应力，σF表示有限元计算结果。分析如下：

（1）如图13 所示，在主船体底部，梁理论、双梁理论及修正双梁理论计算得到的纵向应力基本一致，但与有限元计算结果相差较大，这是由于在有限元计算中考虑了水压力的作用，而理论计算中并未考虑水压力，其次在实际计算中邮轮上层建筑并不能完全参与总纵弯曲，相较于梁理论中上层建筑100%参与总纵弯曲，主船体分担的载荷较大，因此有限元计算得到的主船体底部纵向应力会大于理论计算结果。

（2）甲板高度在内底板与一层甲板之间，双梁理论计算纵向应力与有限元计算结果基本吻合；由于上层建筑和主船体的刚度不同，在主甲板处，应力值发生突变；甲板高度高于一层甲板后，双梁理论计算结果随高度方向呈线性变化，与有限元计算结果差值不断变大。

（3）随着甲板层数的增大，修正双梁理论与有限元结果差值逐步减小，到第三层甲板时应力重合；而梁理论计算应力随高度方向呈线性变化，无法模拟上层建筑的真实应力变化。修正双梁理论计算结果相较于梁理论，更接近真实的纵向应力分布。

4 结 论

本文基于双梁理论提出了计算邮轮纵向应力沿高度分布的修正方法，在保证计算结果精确性的前提下，简化了双梁理论的计算过程，对邮轮纵向应力沿高度分布特性研究具有重要意义。

本文主要研究结论如下：

（1）当梁的高度远小于跨度时，梁理论一般会忽略横向剪切变形的影响，但由于大型邮轮拥有多层上层建筑，致使横向剪切变形的影响变得不可忽略。本文基于梁理论，对弯曲及剪切变形产生的应力进行了理论推导。

（2）运用双梁理论分析邮轮主船体和上层建筑之间的相互作用，引入剪切滞后系数r对上层建筑所受弯矩进行修正。

（3）以一艘典型内河邮轮为研究对象，采用简单梁理论、传统双梁理论及修正后的双梁理论计算方法对邮轮船舯剖面进行强度评估，数值计算结果表明，修正后的双梁理论计算结果与有限元计算结果更为吻合。