复杂地层中盾构掘进参数计算与研究

刘军华，傅鹤林

(1.中化学建设投资集团有限公司, 北京 100000；2.中南大学 土木工程学院，湖南 长沙 410075)

随着城市地下空间的开发，盾构施工越来越普遍[1]。对于不同条件下的盾构掘进参数计算，不少学者对此做了大量的研究。Barton[2]依据经验预测方法，参考岩体质量指标Q，基于引入了掘进参数得到QTBM预测模型，预测了推进速度；Bruland[3]在室内试验的基础上，分析盾构施工参数数据，得到可以预测推进速度等掘进参数的NTNU模型；而Bruines[4]基于模糊神经网络模拟，构建了预测TBM的施工进度的模型；付柯[5]基于掘进参数与推进速度间相关性的分析，提出了带交互项的预测方法，构建了推进速度优化数学模型及交互式的推进速度多目标优化方法；蒋斌[6]基于实地监测、施工数据，以最大地表沉降值和单环推进速度为输出目标，构建了 BP 神经网络模型，获得了掘进参数多目标优化方法。王强[7]采用数理统计的方法，以小浪底引水干线盾构工程为依托，分析了关键掘进参数间的关联性，提出了复杂富水地层下，盾构推进速度与刀盘扭矩的多元回归模型，优化了参数进行。王洪新等[8-9]采用理论分析和试验的方法，基于建立的土压平衡盾构掘进的数理模型，进一步推导了几个关键参数间关系的数学表达式。章邦超等[10]针对其地层分布复杂、软硬差异大及穿越密集民房建筑群等特点，通过注浆加固、现场动态监测、优化掘进参数等一系列主动措施，解决实际工程中掘进参数合理取值与地表建筑沉降变形控制两大难题。肖昌军等[11]以南宁市轨道交通5号线新广区间盾构隧道工程为背景，考虑了刀盘刀具破岩荷载以及盾构-土相互作用的影响，利用MATLAB软件进行了盾构作用荷载静力平衡方程的矢量计算，得到了斜穿地下连续墙的盾构推进力。戴志成等[12]以广佛环线沙堤隧道为工程依托，利用有限差分软件研究了土压平衡盾构水下始发段掘进参数对地表沉降的影响，并结合现场实测数据分析了盾构掘进过程中地表沉降和邻近建筑物变形的变化规律。张建国[13]采用三维有限元计算方法，模拟了盾构施工全过程对高铁桥梁基础、墩台、轨道沉降、倾斜规律进行了预测分析，确保了铁路运营安全。王凯等[14]建立了掘进载荷数学模型，基于土岩交互地层模型、刀盘几何模型对载荷计算模型进行了数值仿真，分析了基岩侵入高度、岩石强度、贯入度等影响因素对刀盘转矩的影响规律。炊鹏飞[15]通过采取掘进施工前对下穿建(构)筑物进行鉴定评估、隔离加固，掘进过程中合理选择与优化掘进参数、地表跟踪注浆,下穿通过后洞内补充注浆等风险控制措施，对盾构下穿建(构)筑物风险控制技术进行研究。

国内外研究表明：不同施工条件下的掘进参数会有较大的差别，研究复杂地层环境和不同工程条件下的盾构掘进参数，仍是隧道工作者迫切需要解决的难题。因此，本文依托于安庆市污水尾水管穿越石门湖通道工程，结合复杂的工程地质条件和盾构机参数，提出盾构掘进过程中的总推力和刀盘扭矩计算模型，分析其影响因素，并计算单刀破岩垂直力及其与中间主应力系数的关系。为石门湖通道工程提供技术支持，也可为类似工程提供技术参考。

1 工程概况

1.1 工程背景

本工程位于安庆市高新区，项目范围为山口片区东部、石门湖以及凤凰片区西部。安庆市高新区山口片区位于安庆市老城区西北方向，距安庆市区7.5 km，地属安庆市大观区山口乡及十里铺乡。山口乡位于安庆市西郊，距206国道12 km，东濒石门湖与十里铺乡接壤，南临皖河与海口镇隔河相望，西与洪铺镇毗邻，北与月山镇相连。

过湖通道横跨石门湖东西两岸，平面线形呈直线设置，东接接收井，西连始发工作井，过湖段总长2 165 m，过湖通道采用盾构法施工。详见图1。

图1 污水管过石门湖工程平面示意图

盾构掘进过程中，依据本工程的工程地质和水文条件选择土压平衡盾构机，盾构机的具体参数为：整机长度约84 m，最小水平转弯半径250 m，爬坡能力为±50‰，推进速度不小于80 mm/min，开挖直径6.46 m，驱动功率645 kW，驱动扭矩6 846 kN·m，脱困扭矩8 687 kN·m，最大推力42 575 kN。

1.2 工程地质条件

根据勘察结果，结合区域工程地质资料，线路所经地段钻探揭露地层有：①杂填土：松散，厚度0.9 m～13.5 m。②耕土：干燥—潮湿，厚度0.5 m～2.2 m。③淤泥：软流塑，饱和。厚度0.5 m。④粉质黏土：可塑，厚度1.0 m～3.7 m。⑤卵石土：饱和，该层场地内一般分布在基岩表面，局部缺失。⑥强风化砾岩：岩芯多呈2 cm～8 cm碎块状，风化残块质软。胶结程度较差，风化程度不均。⑦中风化砾岩：岩芯完整程度跟砾石含量有关，多呈5 cm～40 cm柱状。地层的具体力学参数见表1。

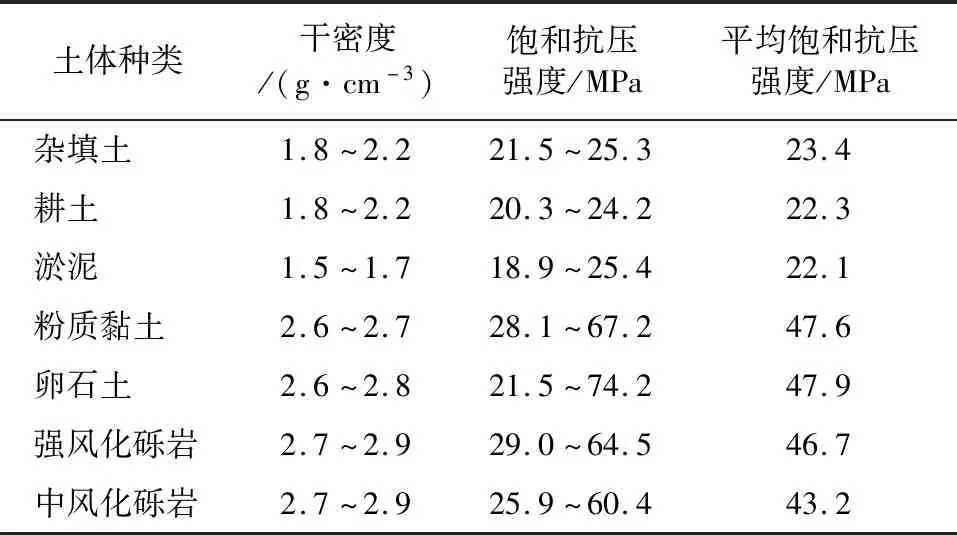
表1 不同地层岩石力学性质统计

1.3 工程水文条件

安庆高新区山口片区东临石门湖，南依皖河，基地南侧自然河湾成为规划区特色，现状湖泊与集中区用地相嵌，自然生态环境良好。拟建场区南端距离长江约2 km，地下水和地表水与长江水基本连通。场区赋存四种地下水类型，分别为上层滞水、孔隙潜水和基岩裂隙水。

2 盾构掘进参数模型优化

2.1 中间主应力系数

在岩体塑性理论中，常以Lode参数μ表示应力参数：

(1)

式中:σ1为大主应力；σ2为中主应力；σ3为小主应力。

本文定义中主应力系数β，来研究中主应力效应。

(2)

式(2)变形得

σ2=βσ1+(1-β)σ3(0≤β≤1)

(3)

不难证明，μ与β之间有如下关系:

μ=2β-1

(4)

不难得出，一般三轴试验状态(σ1>σ2=σ3，三轴压缩)β=0，μ=-1；真三轴试验极限状态(σ1=σ2>σ3，三轴拉伸)β=1，μ=1。

2.2 滚刀-岩体作用模型

隧道掘进机滚压破岩的机理认为：推力和扭矩通过刀盘传递给滚刀，使滚刀在贯入岩石的同时产生滚动，从而破碎掌子面。因此，滚刀-岩体作用模型的科学建立对准确预测破岩力、掘进机推掘系统的合理设计、刀具和刀盘的参数优化等具有重要的工程意义。近年来，常截面(CCS, Constant Cross Section)滚刀模型在工程实践中得到了较为广泛应用[13]。依据CCS模型，在常截面滚刀与掌子面岩层接触弧线上任取一个岩石单元体进行应力状态分析，重点考虑刀岩接触面上指向滚刀中心力σ1的计算方法。在滚刀应力σ1的作用于单元体的同时，周围岩体垂直于该单元体侧表面也施加了大小为σ2和σ3的围压，此时研究对象为真三轴应力状态，如图2所示。

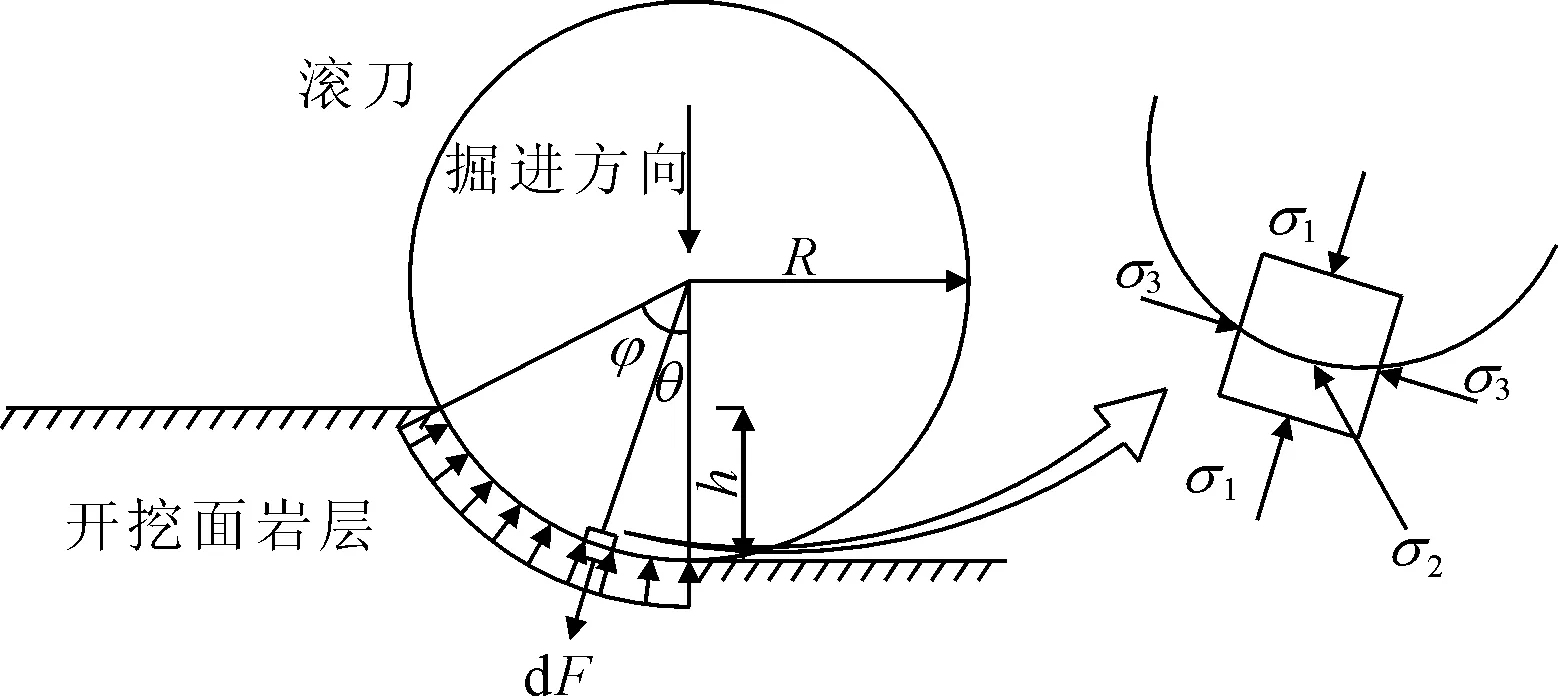
图2 常截面滚刀下压力分布图及岩石单元应力状态图

对岩石单元体的极限接触压力沿接触弧面积分，积分单元及受力分解如图3、图4所示，可得到滚刀受力的近似计算公式:

(5)

式中:Fr为总推力提供的掘进方向滚刀的切向滚动力；Fn为刀盘扭矩提供的掘进方向滚刀的法向垂直力；W为滚刀刀刃宽度；R为滚刀半径；θ为刀岩接触方向与竖直方向的夹角；φ为刀岩接触面弧度；ψ为压力分布函数常量，取0.1；p0为Rostami[10]通过一系列实验和回归分析得到的盘形滚刀正下方基准压力计算值，有:

(6)

将式(6)中单轴抗压强度σc替换为真三轴应力状态下的大主应力σ1，有:

(7)

式中:σ1为岩石抗压强度；σt为岩石抗拉强度；S为刀刃间距；C为无量纲常数，取2.12。令h为滚刀贯入度(mm)，由图2几何关系可得：

(8)

一般情况下，岩土类材料抗压强度σc为抗拉强度σt的8倍～12倍，取σt=0.1σc且(2R-h)≈2R，可得：

(9)

CCS模型所采用的室内全尺寸线性切割试验岩样与盾构机现场掘进岩体还是存在一定区别的，特别是忽略了岩体不连续结构面(节理等)和软硬交互岩层等对掘进机性能的影响，使得模型表示的是完整岩石中掘进所需最大破岩力，计算结果较为保守和安全，对盾构刀具刀盘的设计具有更重要意义。

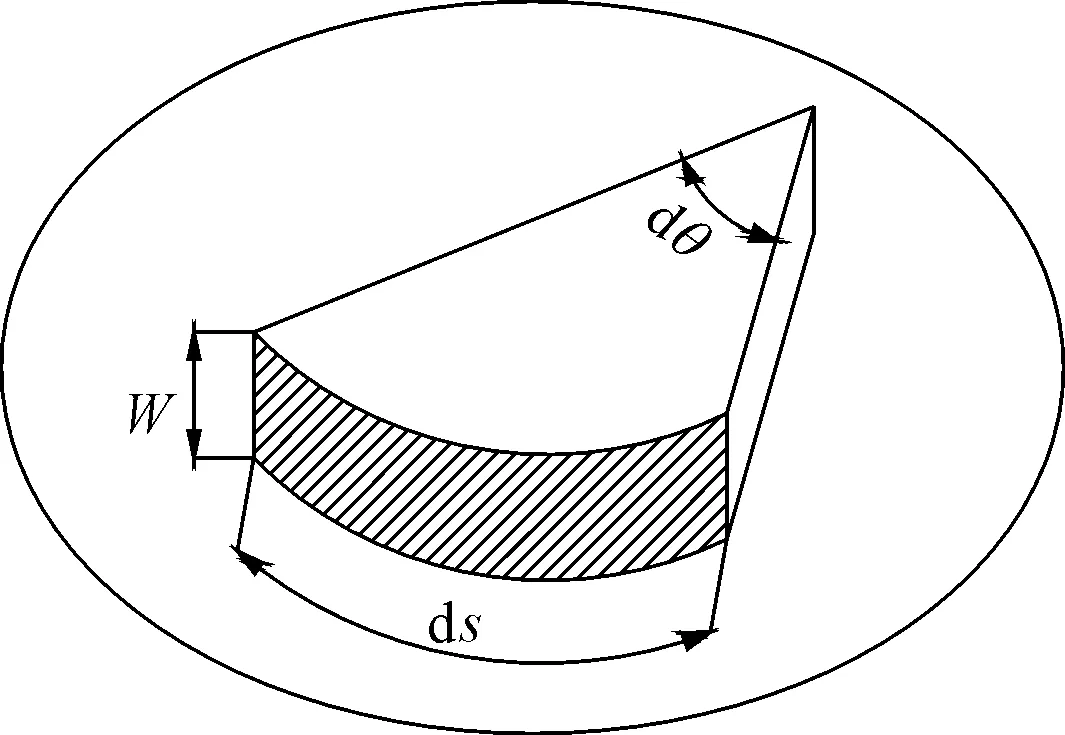
图3 滚刀破岩力计算积分单元

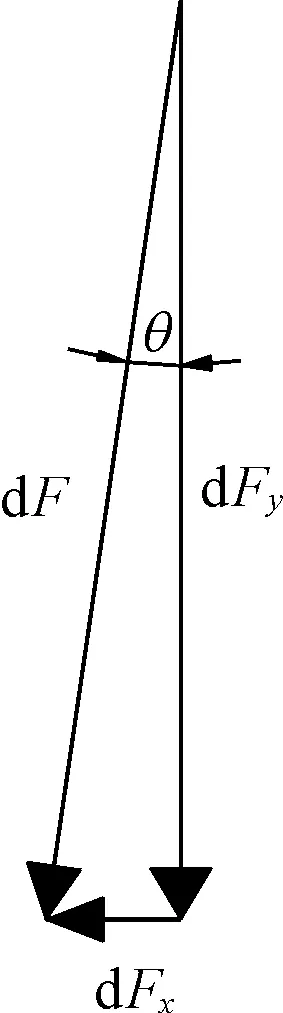
图4 滚刀破岩力分解图

2.3 掘进参数计算模型

2.3.1 掘进参数的选取

考虑中主应力系数β的不同岩石强度准则对盾构机总推力F和刀盘扭矩T的计算会产生直接影响，进而影响到盾构机具的选型与施工技术方案的评估。

2.3.2 总推力计算模型

复合式隧道掘进机推力F包括：盘形滚刀破碎掌子面岩层的推力F1；盾体克服围岩摩擦阻力的推力F2；刀盘稳定掌子面侧向压力的推力F3；掘进机后配套设备牵引力F4；克服盾尾与管片间摩擦阻力的推力F5；曲线掘进时克服变向阻力的推力F6。因F1～F3约占总推力的90%～95%，所以F4～F6的影响忽略不计，如图5所示，则复合式隧道掘进机总推力计算式为：

F=F1+F2+F3

(10)

图5 复合式隧道掘进机掘进方向总推力受力图

刀盘掘进破岩所需推力F1可近似表示为:

(11)

式中:N为刀盘上安装的滚刀数(忽略中心刀、面刀和边刀的区别)。

借鉴Rad等的滚刀破岩推力计算模型，盾壳克服地层摩擦阻力的推力F2计算式为:

F2=πfsDL(p1+p2+p3+p4)/4

(12)

其中:

(13)

式中:D为盾构机外径；L为盾构主机长度；fs为地层与盾壳之间的摩擦系数；G为刀盘质量；K为岩体侧压力系数；p1为盾构机上部压力；p2为盾构机底部压力；p3为盾构机上部侧压力；p4为盾构机底部侧压力；γ为岩体的重力密度。

刀盘承受开挖面压力所需的推力F3为:

(14)

其中:

Pd=Kγ(2D+D/2)

(15)

式中:Pd为刀盘轴线处的侧向压力；k0为岩体压力系数。

2.3.3 刀盘扭矩计算模型

复合式隧道掘进机扭矩T包括：盘形滚刀切削岩体时地层抗力扭矩T1；刀盘正面与开挖面间摩擦阻力扭矩T2；刀盘背面与压力舱内碴土间摩擦阻力扭矩T3；刀盘侧面与岩层间摩擦阻力扭矩T4；土压舱搅拌叶片搅拌扭矩T5；减速装置摩擦损失扭矩T6；轴承引起的摩擦阻力扭矩T7。因T1～T4约占刀盘扭矩的70%～90%，所以T5～T7的影响忽略不计，则复合式隧道掘进机扭矩计算式为：

T=T1+T2+T3+T4

(16)

其中:

(17)

式中:F1为刀具破岩时所需推力；K1为切削系数；H为地表到盾构机轴线的垂直距离；P0为开挖面平衡压力；d为刀盘外沿宽度；η为刀盘开口率。

2.4 真三轴工况下掘进参数计算

根据盾构的配置参数，选取十个典型断面进行研究，各断面情况如表2所示。

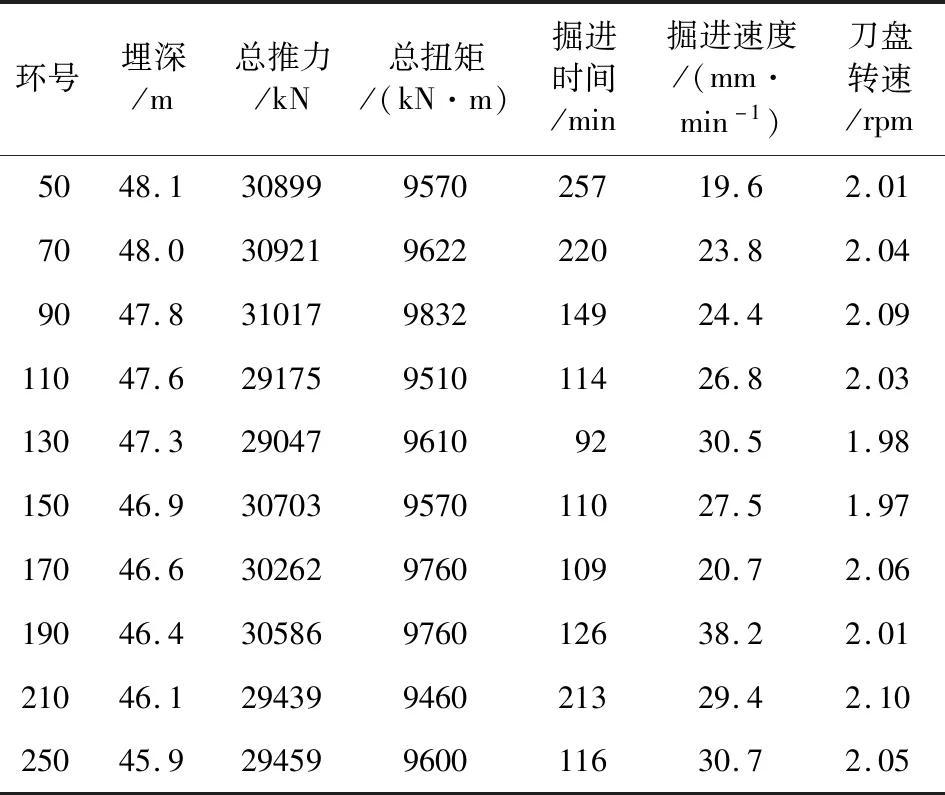
表2 盾构掘进50～250环典型断面掘进数据表

典型断面主要计算参数如表3所示。

表3 典型断面主要计算参数表

根据总推力计算公式，在表2所示典型断面总推力实测值中去掉盾壳克服地层摩擦阻力的推力F2和刀盘承受开挖面压力所需的推力F3，即可得到刀盘滚刀破碎掌子面岩石所需推力F1的实测值；结合盾构机的配置参数，进一步计算可得每把滚刀破碎开挖面所需的平均推力Fn1(垂直力)的实测值，如表4所示。根据刀盘扭矩计算理论，在表2所示典型断面刀盘总扭矩实测值中去掉T2、T3和T4，即可得到盘形滚刀切削岩体时地层抗力扭矩T1的实测值；结合盾构机的配置参数及式(16)，进一步计算也可得到破碎开挖面所需推力F1和每把滚刀所需平均推力Fn2(垂直力)的实测值，如表5所示。

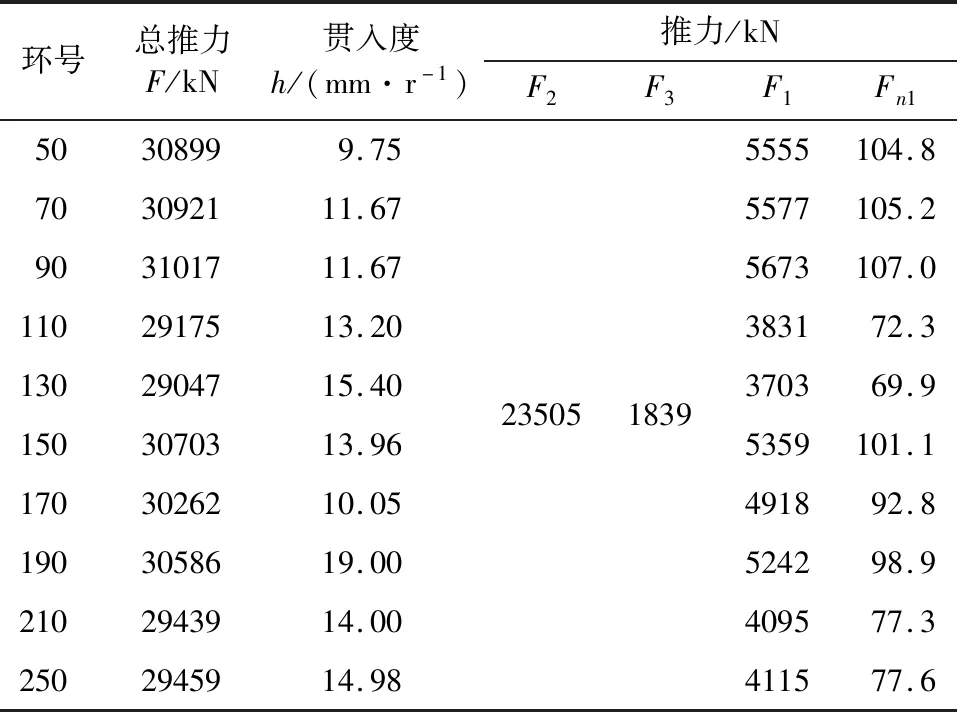
表4 典型断面掘进推力计算表

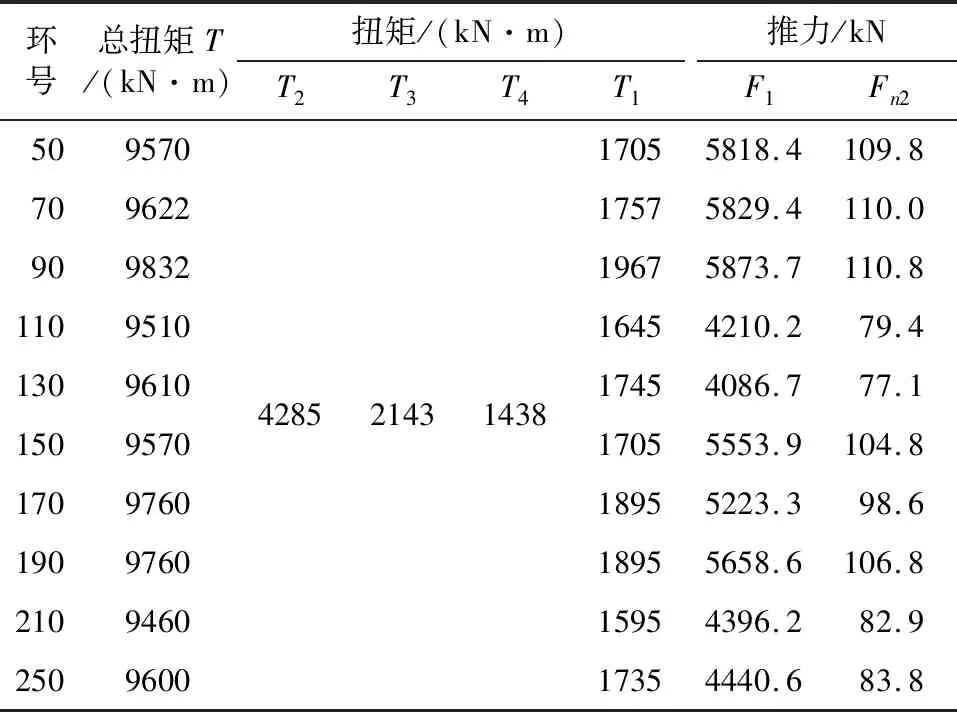
表5 典型断面刀盘扭矩计算表

结合地层中主应力系数β，将根据推力和扭矩模型分别计算得到的接触面单刀破岩垂直力Fn1和Fn2进行对比，如图 6所示。可以看出：Fn1和Fn2变化趋势相同且相差不大，差值均小于10 kN，相互定量证明了两个模型中对F2～F6、T2～T7的计算及简化方法是基本正确的，且现场采集的数据具有较高可信度；中主应力系数β与单刀破岩垂直力Fn的关系成反相关；在工程实际中，中主应力系数β取值一般小于0.1，较难遇到β取0.2～0.5的情况。为使单把滚刀破岩垂直力计算更为精确并消除误差等的影响，将推力和扭矩模型计算得到的Fn1和Fn2取平均值得到Fn，如表6所示。计算得到的数据对盾构掘进过程中控制掘进参数有着非常重大的作用。

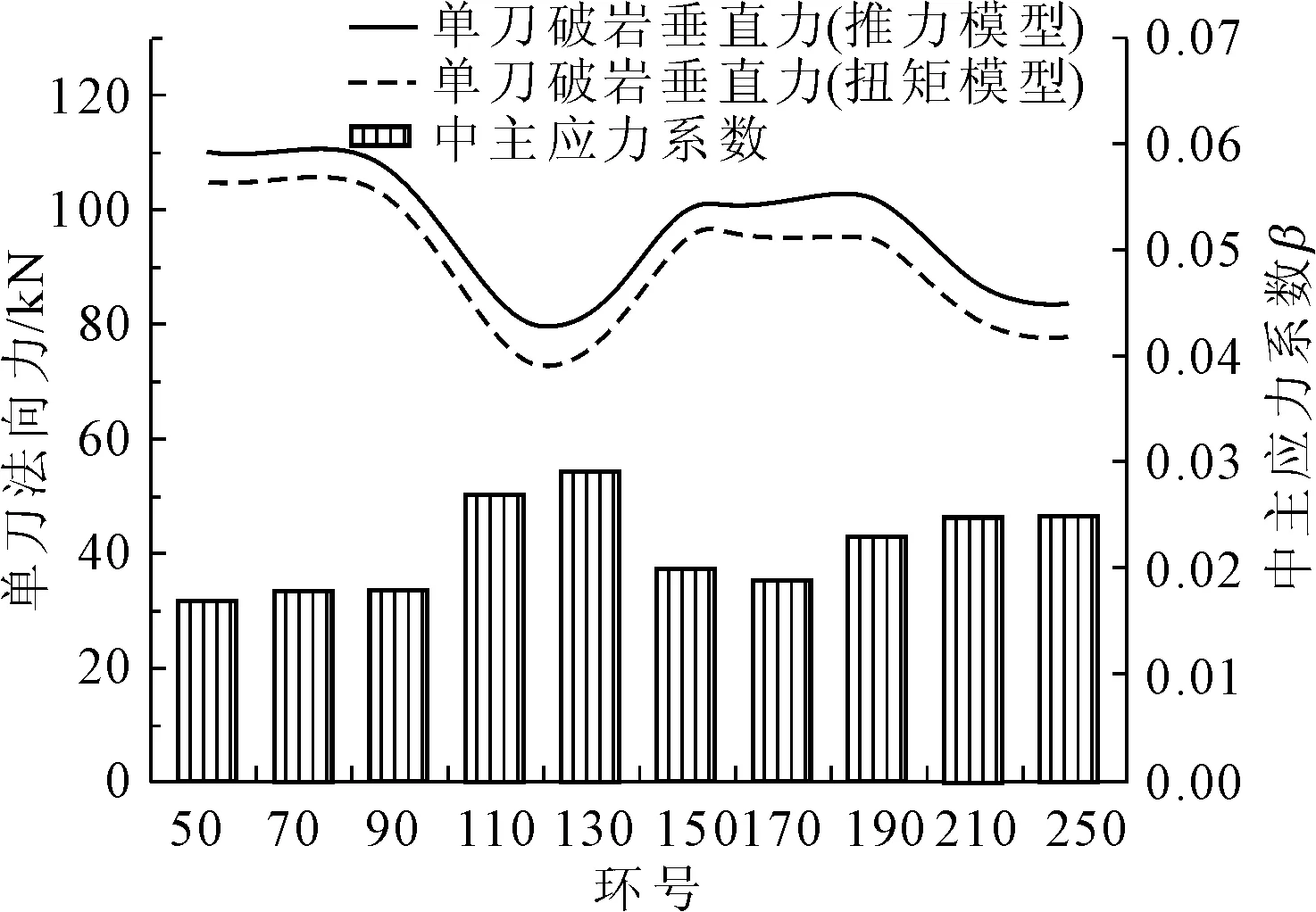
图6 单把滚刀破岩垂直力变化图

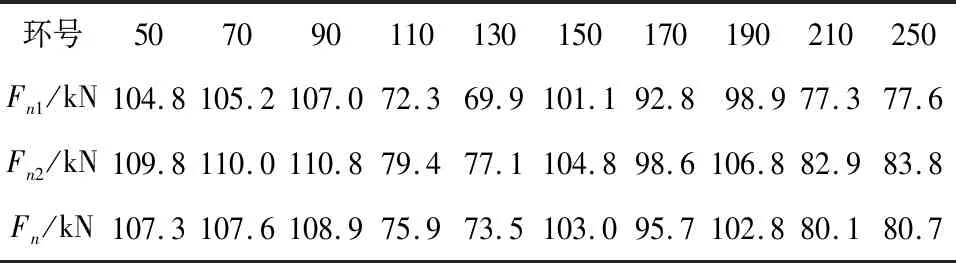
表6 单把滚刀破岩垂直力平均值

3 结 论

安庆市污水尾水管穿越石门湖通道工程主要穿越淤泥质粉质黏土、粉质黏土、卵石土、强风化砾岩和中风化砾岩，地质复杂，软硬不均，含水量高，如何选择掘进参数成为盾构施工技术的关键，通过研究得到如下结论：

(1) 基于美国科罗拉多矿业学院常截面滚刀线性切割实验模型，通过对滚刀正下方刀岩作用单元基准压力计算方法的修正，并在相关资料的基础上优化了滚刀破岩时所需滚动力和垂直力的计算公式。

(2) 选取了盾构机掘进过程中所需总推力和刀盘扭矩值作为现场实测参数，结合相关研究资料，分析了这两项指标的构成、影响因素和简化计算方法。

(3) 以安庆市污水尾水管穿越石门湖通道工程为工程背景，选取了10个典型断面，提取了掘进总推力和刀盘扭矩实测值中与滚刀破岩相关的部分，单独考察了单把滚刀破岩垂直力，单把滚刀破岩垂直力与中主应力系数β成反比。