温-湿耦合环境下黄土遗址水分迁移规律试验和数值模拟研究

周 恒，狄圣杰，黄 鹏，李嘉伟，刘奉银，穆青翼

(1.中国电建集团西北勘测设计研究院有限公司，陕西 西安 710065；2.西安交通大学 土木工程系，陕西 西安 710049；3.西安理工大学 岩土工程研究所，陕西 西安 710048；4.西北旱区生态水利国家重点实验室，陕西 西安 710065)

土遗址是指人类历史上以土作为建筑材料所留下的关于生产、活动等遗迹[1]。在我国的黄河和长江流域留存着大量的土遗址，这些土遗址是我国几千年历史的重要载体，可以反映特定历史时期社会的经济、技术和文化发展水平，具有极高的研究价值[2-3]。然而，土遗址由于自身材料属性并且多暴露于开放的大气环境中，在自然因素下极易受到多种因素损害，例如：冻融、盐蚀、干缩开裂等[2-3]。

以中国西北黄土地区为例，在干旱、半干旱的气候下，干缩开裂是本地区土遗址面临的主要灾害问题。干缩开裂的物理机制是土体在失水过程中吸力变化引起的张拉应力超过了土体本身的抗拉强度，从而造成开裂。土遗址内含水率的变化直接关系到土遗址是否会开裂，所以研究土遗址中水分的分布规律极其重要。张悦等[3]结合持水特征曲线研究了含盐土遗址开裂的机理及影响因素。崔凯等[4]等研究了毛细作用对干旱区土遗址底部掏蚀区发生盐渍劣化效应的作用机理，并提出了相应的理论模型。谌文武等[5]研究了融雪与降雨对含盐土遗址劣化机理，结果表明降雨易使水盐富集造成结构破坏，而融雪促进了盐分分散，有利于土遗址结构恢复。土柱试验是研究土壤中水分迁移机理的重要试验，但是，目前相关的土柱试验研究主要集中于各类原状土研究，且主要应用于降雨导致的滑坡、土壤的湿陷性等方面。Ng等[6]通过土柱试验研究了表面应力对土壤渗透性的影响。Liu等[7]通过土柱试验研究了降雨对边坡失稳的影响。综上所述，目前尚缺乏采用土柱试验对压实土在温-湿耦合作用下土体水分迁移规律的研究。

针对温-湿耦合作用下黄土遗址中水分迁移规律研究，本文首先开展了土柱蒸发试验，测试不同密实度下非饱和黄土水力学特性，即持水特征曲线和非饱和渗透系数。其次，基于室内测试的水力学参数和现场的监测数据，采用非饱和土渗流分析软件对兵马俑遗址一号俑坑在温-湿耦合环境下的含水率和吸力分布规律进行模拟分析。

1 试验概况

1.1 试验材料与试样制备

本试验所用黄土取自西安某基坑，在地表之下5 m进行取样。按照《土工试验标准》[8](GB/T 50123—2019)，对黄土进行基本物性指标测试，结果如表1所示。将所取黄土和文献[9]中兵马俑夯土基本物性参数进行对比，两者基本一致。

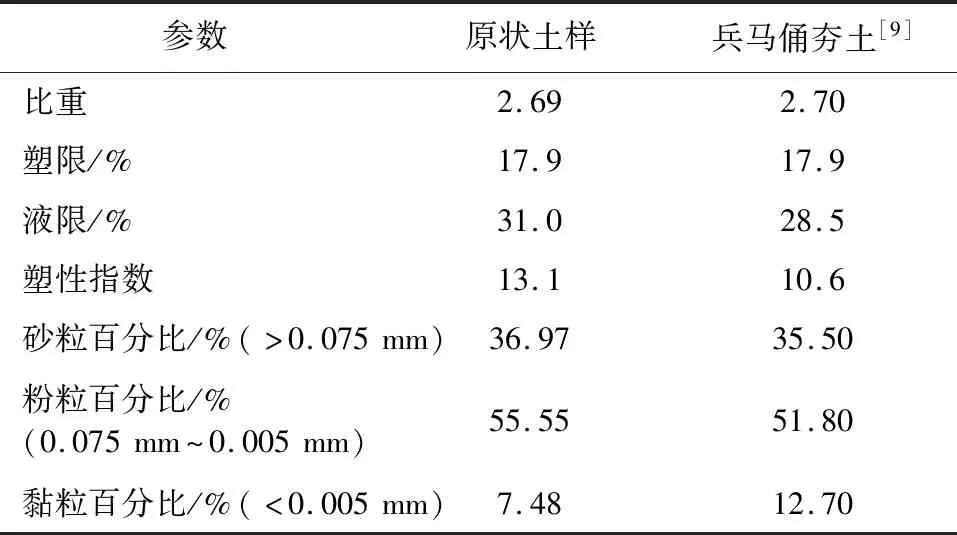
表1 试验黄土基本参数

为制备目标条件下的压实黄土，将所取黄土在105℃下烘干24 h并过2 mm标准筛。随后采用自来水与过筛后的黄土均匀混合并设置质量含水率为13.2%。最后，将所配制黄土在塑料袋中密封放置48 h，以保证水分均匀分布。此外，根据周莉莉等[9]和穆青翼等[10]研究，本文采用干密度1.50 g/cm3和1.35 g/cm3分别作为兵马俑夯土和现场原状黄土的代表值进行室内压实土柱试样的制备。

1.2 试验仪器与步骤

本文基于瞬态剖面法，采用如图1所示的土柱装置进行非饱和黄土持水特征曲线和渗透系数的测试。该装置主要包括5部分：试验土柱，吸力量测系统，含水率量测系统，供水系统以及数据采集监测系统。其中，土柱高100 cm，试验过程土柱高度为20 cm、40 cm、60 cm和80 cm剖面的吸力和含水率变化分别采用4个微型张力计和4个时域反射探头进行量测。另一方面，供水系统主要采用马氏瓶提供恒定水头。

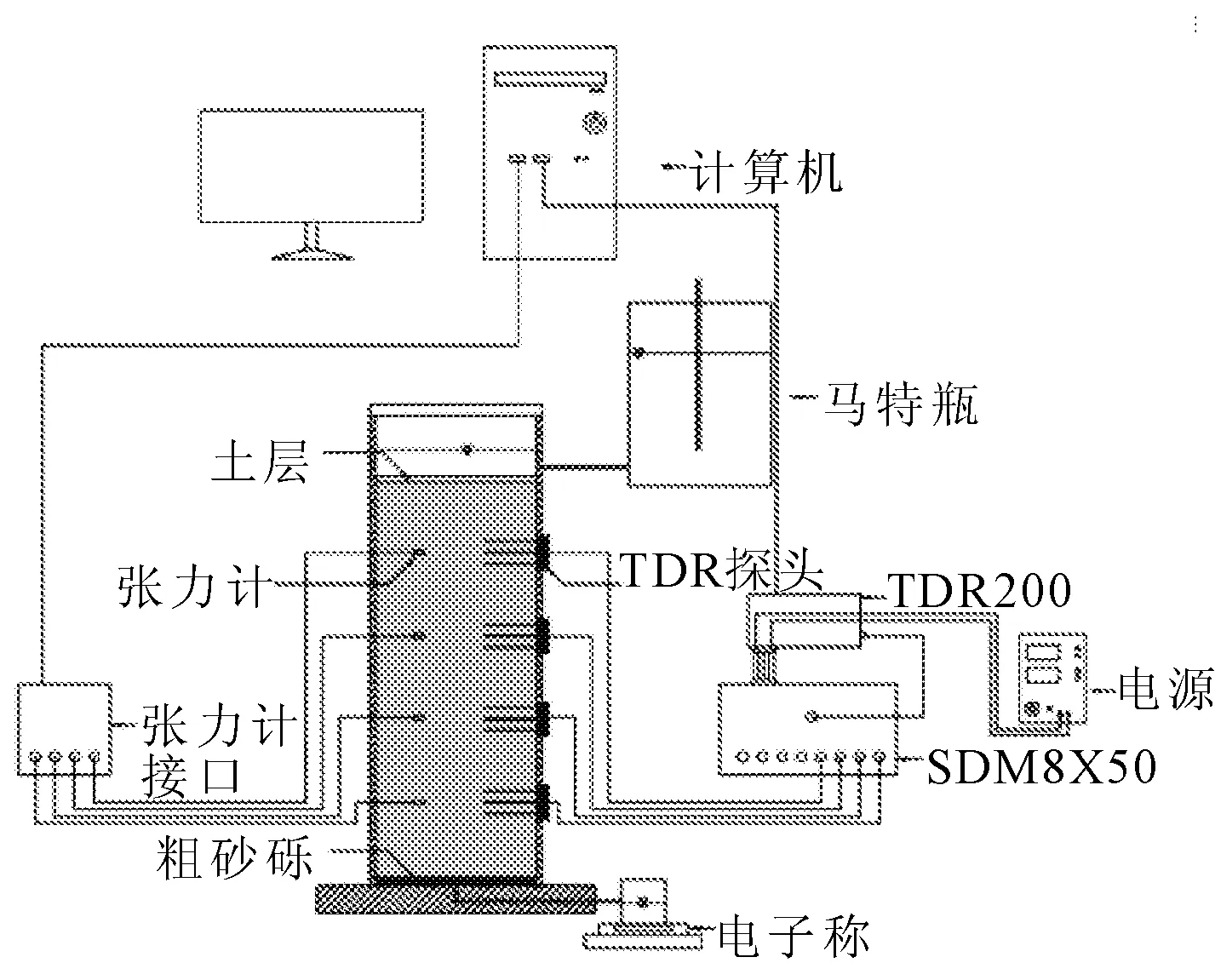
图1 试验仪器示意图

本试验主要包括3个步骤：试样分层击实、土柱饱和与水分蒸发。针对试样分层击实，采用每层5 cm，分两次击实的方法保证制备土柱内黄土密度的均匀，此外，采用层间土壤表面刮毛的方法，避免出现击实分层现象。针对土柱饱和，采用马氏瓶进行恒定水头下的试样入渗饱和，同时根据TDR探头读数和土柱底端渗流水量对土柱内黄土的饱和情况进行监测。针对水分蒸发，当土柱内黄土饱和后，在20℃和40%相对湿度的恒定条件下进行蒸发试验。在蒸发试验过程中，每隔4 h通过数据采集监测系统对土柱的含水率和吸力进行测试和记录，当土体吸力接近张力计量程测试极限时，停止试验。

2 测试原理

2.1 持水特征曲线

持水特征曲线表示吸力和含水率之间的关系，是反映土体持水能力的基本参数。不同密实度的压实黄土在饱和后，进行自然状态下的蒸发。土柱蒸发过程中，通过将相同高度处张力计和时域反射探头的测试结果进行组合，获得土柱内压实黄土蒸发段的持水特征曲线。随后采用式(1)所示van Genuchten模型[11]进行拟合，获得本试验持水特征曲线的模型参数：

(1)

式中:θw表示体积含水率;θr表示残余体积含水率;θs表示饱和体积含水率;φ表示吸力;α与n为拟合参数。

2.2 渗透系数方程

渗透系数方程表示非饱和土渗透系数与吸力的关系，反映了非饱和土渗透性的大小。本文基于土柱蒸发过程中所测试的吸力和含水量随时间变化的剖面数据，采用瞬态剖面法计算非饱和黄土的渗透系数方程。

首先确定渗流介质的总水头，其由位置水头、压力水头和速度水头组成，其中速度水头相对于位置水头和压力水头可以忽略不计，所以总水头表达式可写为：

(2)

式中:hw表示总水头;hg表示位置水头;uw表示张力计所测得的孔隙水压力;ρw表示水的密度;g表示重力加速度。

随后由张力计读数可以得到土柱的总水头剖面图。在某一时间试样内某一点的水力梯度等于该点处水头剖面的坡度，表达式为：

(3)

在某一时间，测点和土柱底端测点之间的总水量Vw可由测得的体积含水率剖面计算得到，其表达式为：

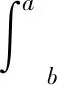
(4)

式中:θw表示该时间体积含水率和深度的函数关系;A为土柱的横截面积;a表示测点位置;b表示底端测点位置。

试样内某一测点的流速vw等于相应时间间隔内该测点与底端测点间总水量的变化率，表达式为：

(5)

非饱和土的渗透系数kw为渗流速度与水力梯度的比值，表达式为：

(6)

由瞬态剖面法计算得到的渗透系数与张力计测得的吸力，可以建立非饱和土渗透系数曲线。本文采用Gardner模型[12]拟合表示kw-θw关系，表达式为：

(7)

式中:a，b均为拟合系数。

2.3 数值模拟原理

2.3.1 模型建立及材料参数

本文建立的模型如图2所示，土遗址横隔梁间的距离取3.0 m，横隔梁的高宽均为2.2 m，在边角处设置长高皆为0.2 m的斜坡，俑坑地面与地下水表面的高差为10.0 m。假设俑坑内3.0 m深以上为夯土，密度均匀分布，3.0 m以下为原状土，密度也均匀分布。土壤的持水特征曲线及非饱和土渗透系数曲线皆取自土柱试验数据的拟合曲线。在模型顶部设置如图所示的温度和湿度边界条件，温度和湿度为兵马俑博物馆内一年间的变化情况[13]，数据如图3所示。在两端设置零流量边界条件。底端设置地下水作为初始水位。在博物馆建成之前，因为遗址表面会受到降雨等的影响，在土壤表面通过模拟降雨增加表面的初始含水率。图2中，点1～点6为用于数值分析的取值点。

图2 兵马俑俑坑几何模型

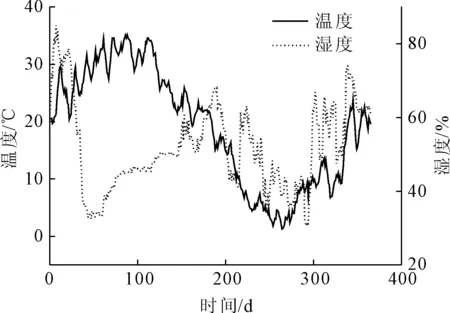
图3 兵马俑博物馆内空气温度和湿度变化图

2.3.2 土体渗流微分方程

非饱和土的二维渗流微分方程的表达式为：

(8)

式中：H表示总水头；kx、ky分别表示水平与竖直两个方向的渗透系数;Q表示边界流量;θ表示为体积含水率;t表示时间。

考虑温度的影响，上述控制方程修改为：

(9)

其中:η表示湿度常数;Pv表示土壤水分蒸汽压力;Γ表示饱和蒸气压和温度关系的斜率;A表示地表相对湿度的倒数;B表示空气相对湿度的倒数;mw表示储水曲线的斜率;rw表示水的重度;RH表示空气相对湿度。

3 试验结果与分析

3.1 土柱蒸发过程中体积含水率和吸力变化规律

图4(a)和图4(b)分别为一号和二号土柱蒸发过程中体积含水率随时间的变化图。其中，一号土柱的干密度为1.35 g/cm3，二号土柱干密度为1.50 g/cm3。从图4(a)可以看出，一号土柱在不同高度处的含水率蒸发速度不同，其中表层15 cm处黄土由于接近大气蒸发较快，而随着深度增加土柱内的含水率蒸发速率依次降低。二号土柱的含水率蒸发趋势与一号土柱具有较好的一致性。然而，二号土柱在35 cm、55 cm、75 cm深处含水率随时间的变化幅度几乎一致，这是因为二号土柱黄土的干密度较大，其持水性相比一号土柱更好。此外，TDR探头测试的初始体积含水率和根据质量-体积关系计算的体积含水率几乎相同，进一步说明了TDR探头测试含水率的准确性。

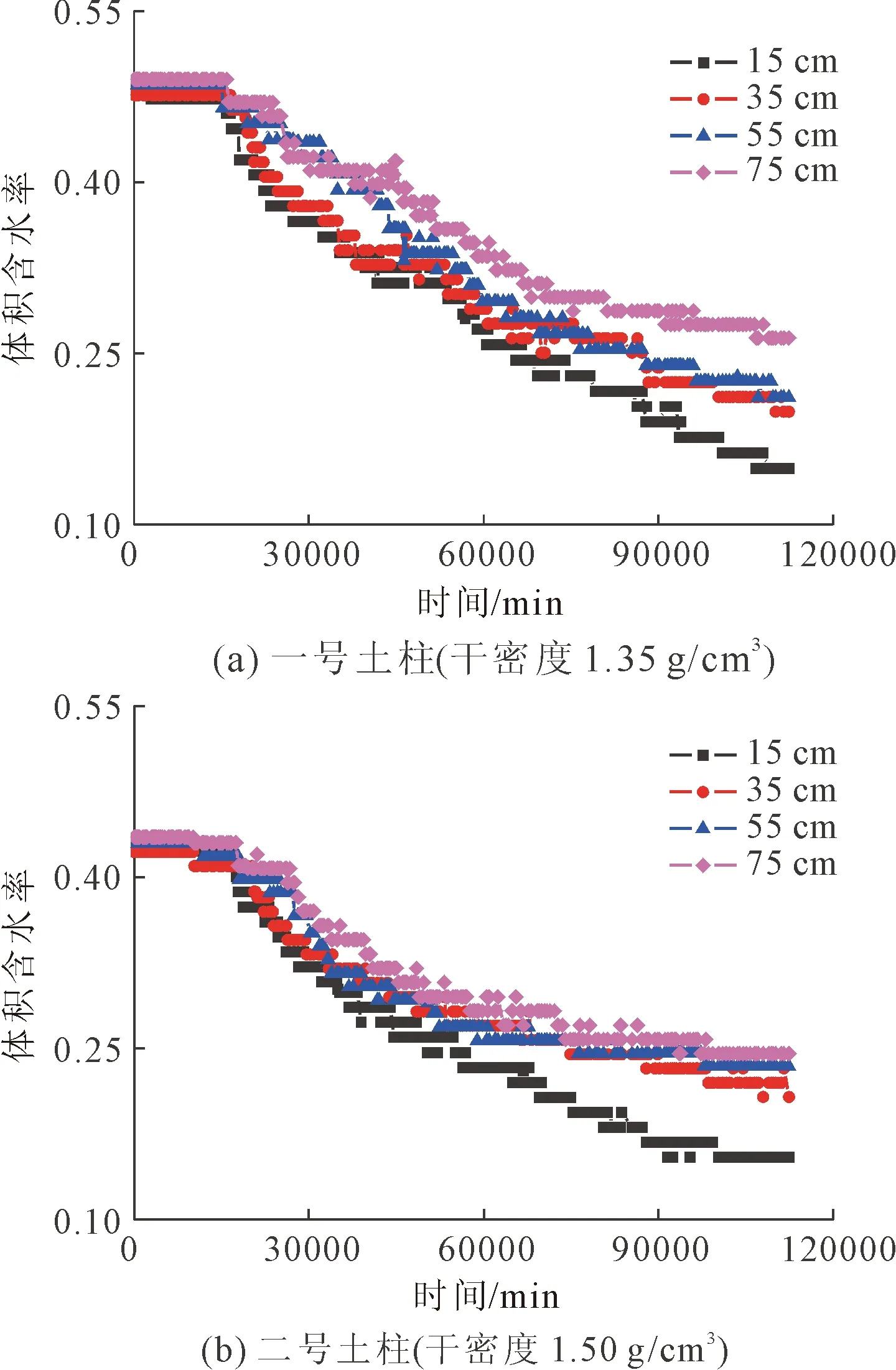
图4 土柱蒸发过程中含水率随时间变化

图5(a)和5(b)分别为一号和二号土柱蒸发过程中吸力随时间的变化图。从图5(a)可以看出，一号土柱在不同高度处的吸力变化在前56 000 min内几乎相同，而在56 000 min后，15 cm深处的吸力出现明显的增大趋势。这是因为一号土柱在56 000 min后表层黄土的失水速率明显增大，而土壤含水率与吸力变化密切相关，如图4(a)所示，约在56 000 min时，一号土柱15 cm深处失水速率增大，与其它深处产生分化。图5(b)所示二号土柱的吸力随时间变化情况与图5(a)相似，其在前40 000 min内土柱不同高度处的吸力变化也几乎相同，而在40 000 min后，15 cm深处的吸力出现明显的增大趋势，这是因为二号土柱在40 000 min后表层黄土的失水速率突然增大。

图5 土柱蒸发过程中吸力随时间变化

3.2 土柱的持水特征曲线和非饱和渗透系数曲线

图6为一号和二号土柱的持水特征曲线。其中，每个土柱的持水特征曲线数据点均取自四个测点的数据。进气吸力值(AEV)为饱和土壤脱水过程中开始进入空气时对应的吸力值，根据Vanapalli等[14]提出的方法，一号土柱的进气值为6.35 kPa，二号土柱的进气值为9.69 kPa。这是因为二号土柱对应的击实干密度较大，在其他条件下相同时，干密度越大，土体的进气值越大。此外，一号和二号土柱持水特征曲线的数据点均存在一定的离散性，这是由于本实验的土柱较高，虽然在制样时采取了相应的防止过击实方法，但在制样过程中土柱的下端还是出现了轻微的过击实现象，从图6中可以看出该误差对进气值的确定几乎没有影响。此外，采用Van Genuchten模型[11]通过Matlab软件对所得的数据点进行非线性拟合，得到持水特征曲线数据点的拟合曲线。其中，Van Genuchten模型[11]拟合参数如表2所示。

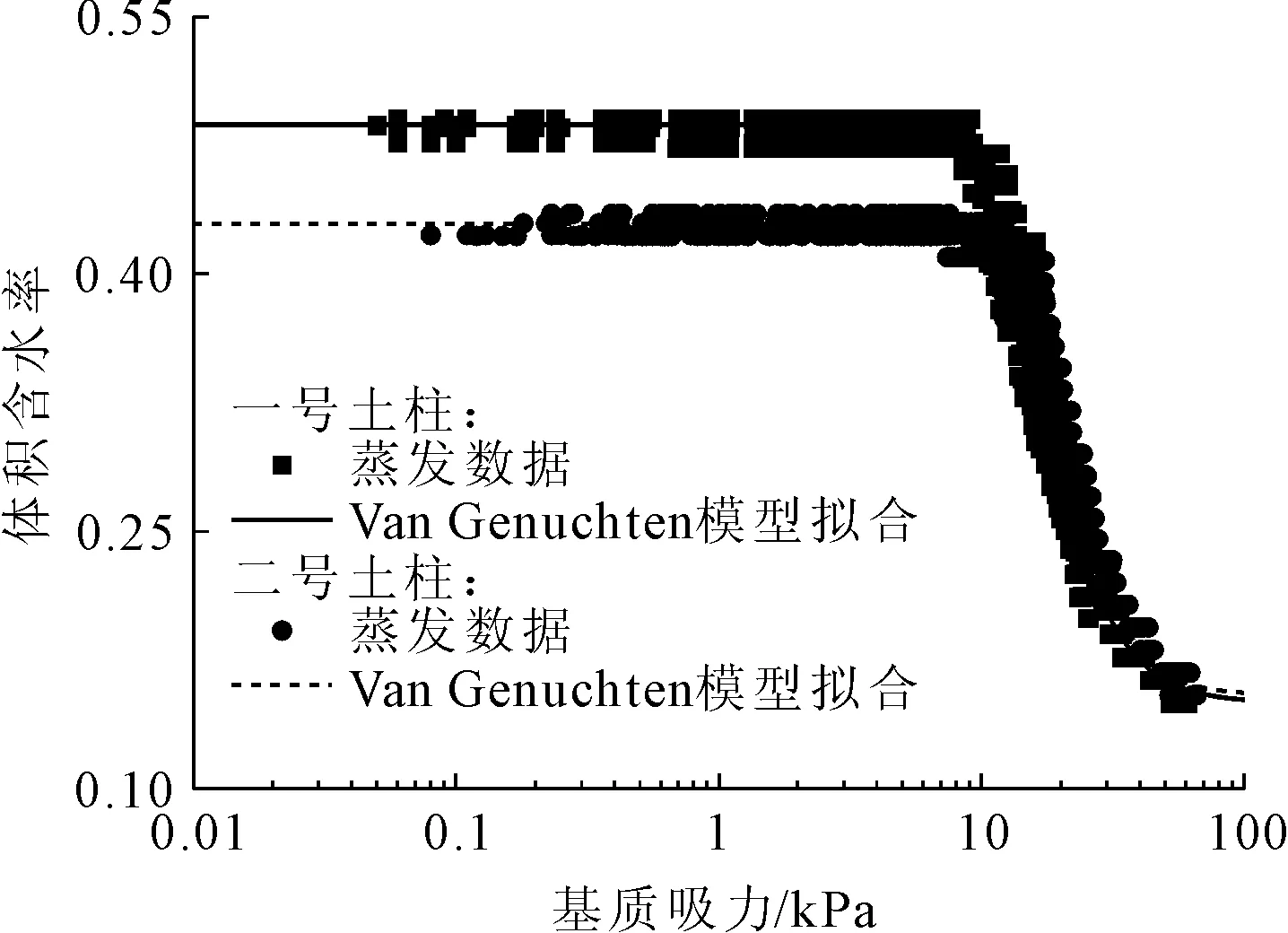
图6 非饱和黄土持水特征曲线

表2 Van Genuchten模型拟合参数

一号和二号土柱的渗透系数曲线如图7所示。从图中可以看出，在饱和阶段，一号土柱的渗透系数明显大于二号土柱，而随着吸力的增加，一号和二号土柱的渗透系数逐渐趋近，这是因为随着吸力增大，水分通过毛细作用的流动逐渐减弱，土体孔隙率对渗透系数的影响也相应的减弱。此外，采用Gardner模型[12]通过Matlab软件对试验数据进行非线性拟合，得到如图7所示的拟合曲线，模型的拟合参数如表3所示。

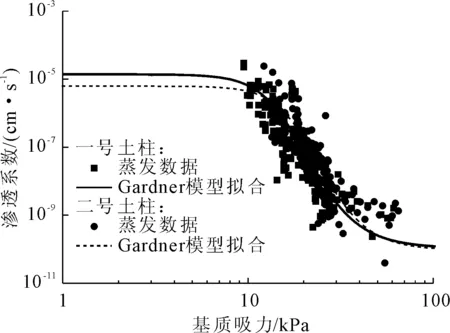
图7 非饱和黄土渗透曲线

表3 Gardner模型拟合参数

4 数值模拟与结果分析

4.1 温-湿耦合条件下兵马俑遗址一号俑坑水分迁移规律

在土遗址表面设置如图3所示的温度和相对湿度条件，对兵马俑遗址进行数值模拟试验。图8(a)和图8(b)分别为温-湿耦合条件下兵马俑遗址一号俑坑水分迁移和吸力变化模拟结果。从图8(a)可以看出前40 d点1、2、3、5处体积含水率下降较快，而点4、6处体积含水率明显上升。这是因为前40 d空气温度较高，相对湿度下降较快，促进了蒸发作用；另一方面，遗址表层水分向下迁移，降低了表层土的含水率，点4、6处体积含水率的上升证明了这一解释。随后，在40 d～160 d间，除了点4、6因为表层水的下渗造成40 d～160 d间含水率较高且下降缓慢外，其余各点处下降趋势较为接近，其中点1处下降最快，点2处因为初始阶段横隔墙顶部表层水分的下渗造成初始阶段体积含水率下降比较缓慢。在160 d后各点含水率下降均较慢，最终各点处体积含水率均稳定保持在10%以下。

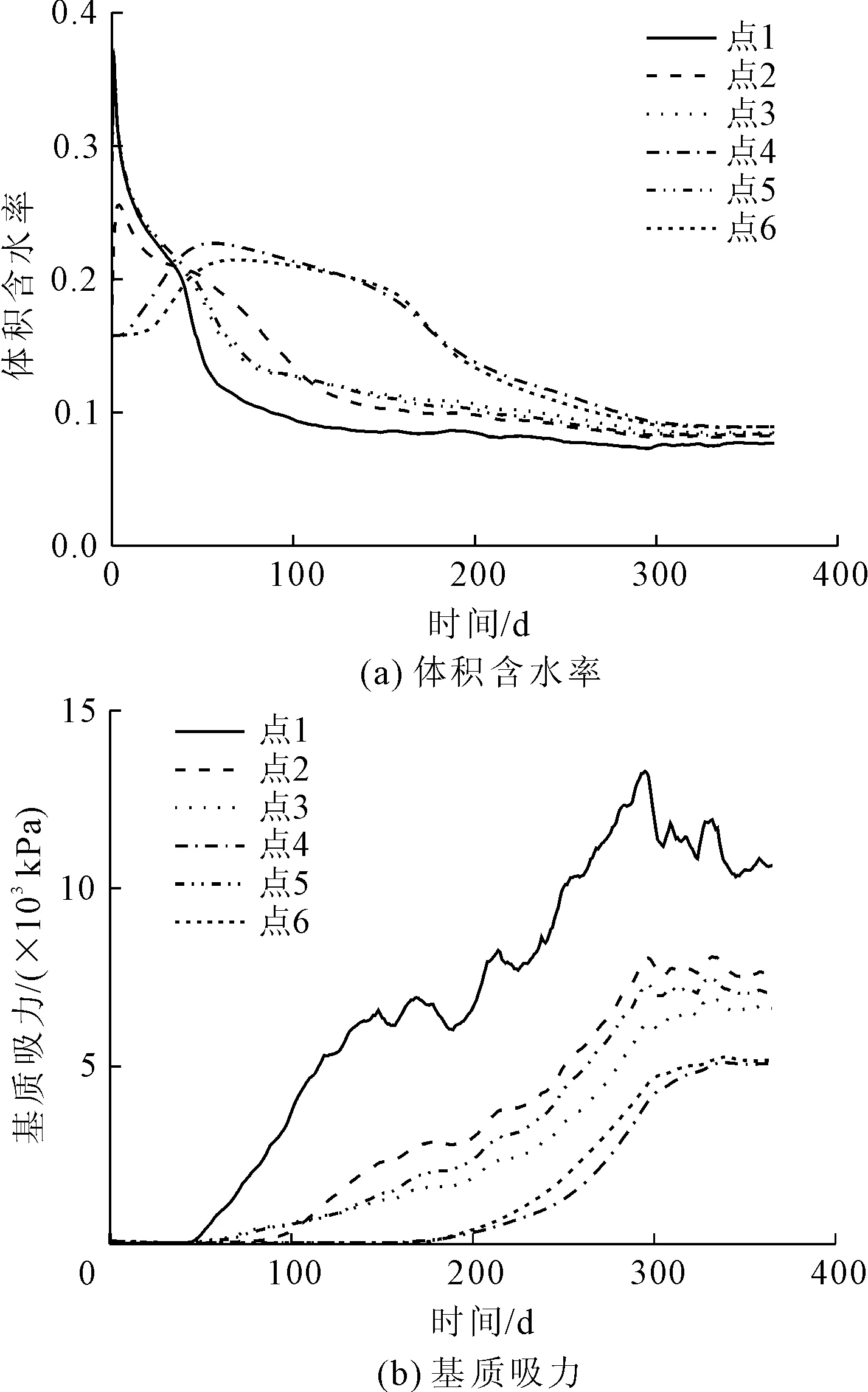
图8 温-湿耦合下土遗址内体积含水率和吸力变化

从图8(b)可以看出前40 d各点处土壤的吸力变化不大，这是因为初始阶段土壤表面饱和率较高，还未达到进气值，故吸力不会有太大变化。在40 d后各点处吸力先后出现快速上升现象，其中以点1最为明显，而在第100 d后由于空气温度出现下降，吸力的上升也有所减缓，同时出现了两次明显的下降趋势，正好对应空气相对湿度的两个峰值，而同为土壤表面的点2、3、5处下降并不明显，这说明土遗址中点1处的土体对空气相对湿度的变化反应敏感。最后，在280 d后点1处吸力出现轻微下降，而其它各点处吸力处于相对稳定状态。此时空气温度正在升高，而相对湿度也在升高，点1吸力的降低说明该处土体对空气湿度变化的灵敏度相对高于对温度的灵敏度。此外，点2、3、5处吸力和体积含水率的变化趋势与数值均较为接近，虽然点2处可以看出失水更快，但是因为有横隔墙的保护，并未出现与地表处明显的区别。点4、6的吸力和体积含水率的变化趋势相似，吸力的数值相对较小，这是因为空气温度和相对湿度难以影响到土壤深处，只能通过表层土进行间接影响。

4.2 恒温-变湿度条件下兵马俑遗址一号俑坑水分迁移规律

在土遗址表面设置20℃的温度和图3所示的湿度条件，对兵马俑遗址进行数值模拟试验。图9(a)和图9(b)分别为恒温-变湿度条件下兵马俑遗址一号俑坑水分迁移和吸力变化模拟结果。图9(a)与图8(a)差距极小，说明温度对于土遗址内含水率的分布影响很小。而图9(b)与图8(b)相比，在恒温条件下土遗址内各点处的吸力整体下降，这是因为在在温度低于20℃时温度对水分蒸发影响较小，而在25℃～40℃之间的高温时会显著促进水分的蒸发。一年中，兵马俑博物馆中温度存在较大变化，高温阶段使变温条件比恒温条件的土遗址失去更多水分。同时，恒温条件下曲线比变温条件下曲线更加平滑，说明温度对曲线形态影响较小，而湿度对曲线形态的影响比温度大。

4.3 变温-恒湿度条件下兵马俑遗址一号俑坑水分迁移规律

在土遗址表面设置如图3所示的温度和55%的相对湿度条件，55%的湿度条件能耗较小且能满足文物保护的需求[15]，随后对兵马俑遗址进行数值模拟试验。如图10(a)所示，模拟体积含水率的下降速度相比前两次数值模拟有所减缓，但曲线形态基本相同。如图10(b)所示，吸力曲线相比前两次数值模拟有很大的变化，在湿度变化情况下原本与200 d～300 d之间的上升趋势变为了变温-恒湿度条件下的下降趋势，曲线整体的吸力相比前两次数值模拟下降较大，而曲线形态与一年间的温度变化曲线刚好对应，高温时增长较快，低温时保持平缓或下降。

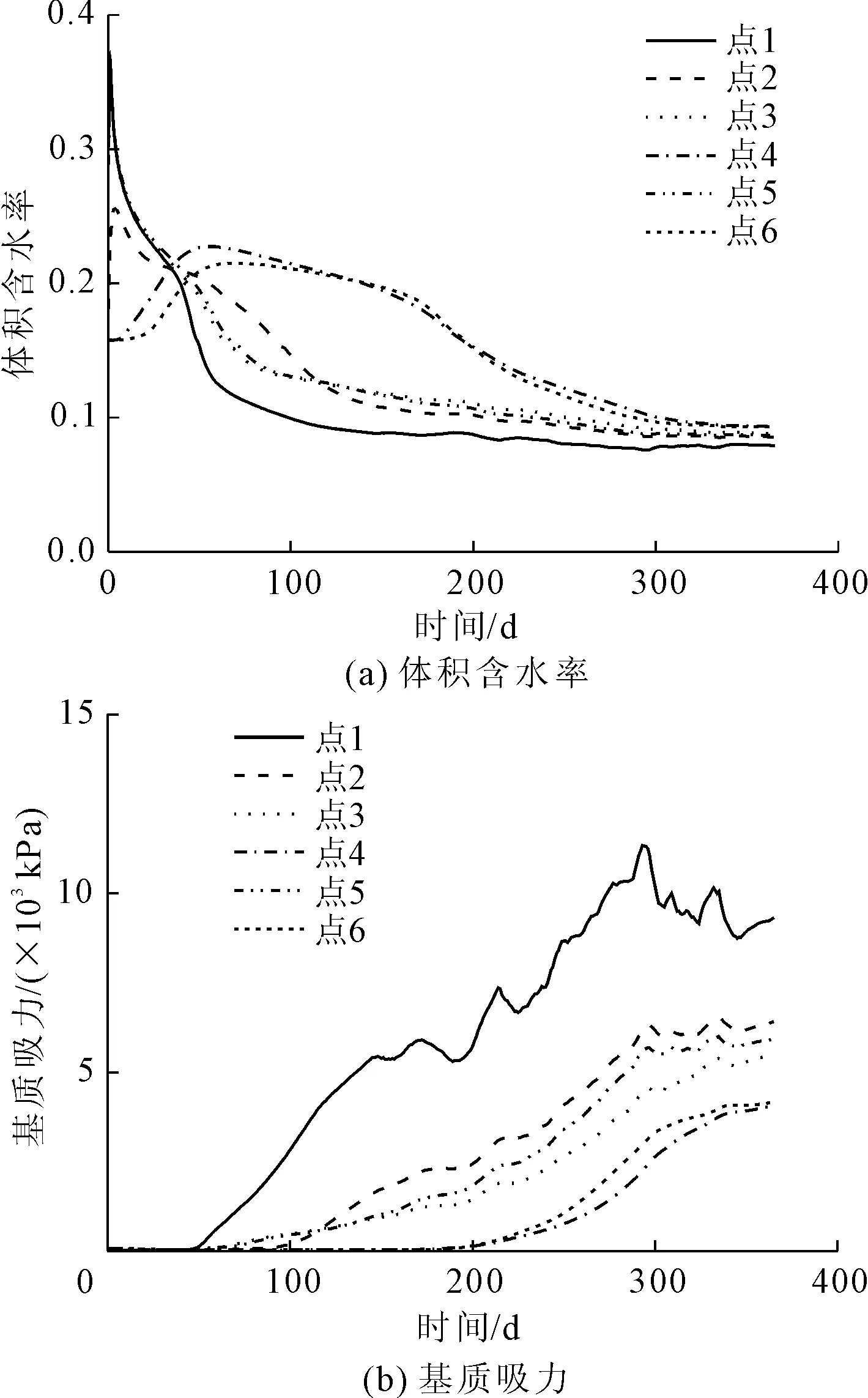
图9 恒温-变湿度下土遗址内体积含水率和吸力变化

图10 变温-恒湿度下土遗址内体积含水率和吸力变化

5 结 论

通过土柱试验，利用张力计及TDR探针分别测量夯土和原状土的体积含水率和吸力，从而得到土壤的持水特征曲线和渗透系数曲线，将其代入非饱和渗流软件中进行数值模拟，对兵马俑博物馆中的土遗址进行数值分析。主要结论如下：

(1) 点1的兵马俑横隔墙顶端拐角处对于博物馆中空气温度和相对湿度的变化反应最为明显，且对相对湿度的变化表现更加敏感。通过控制空气维持较高的湿度，尽量减少空气湿度的波动造成吸力的较大变化，可以较好地保护此处的土遗址。

(2) 低温条件下土遗址内产生的吸力较小，应当在考虑游客舒适性的基础上尽量减小博物馆内的温度。

(3) 土遗址中的体积含水率最终会保持稳定在10%以下，除了横隔墙顶端拐角处外，较高的空气湿度也无法有效降低土遗址内的吸力增大，阻止水分的蒸发，故土遗址的开裂破坏保护更依赖于人工加水，但应避免干湿循环现象，维持含水率稳定。