登高平台电液比例调平系统仿真分析

苗 增，孟凡皓，胡旭杰，段恩业

(连云港杰瑞自动化有限公司，江苏 连云港 222000)

0 引言

随着国民经济的高速发展，登高平台开始在港口码头、建筑物维护、船坞建造、园林、市政等行业得到迅速的推广和应用，国内登高平台的市场需求量不断攀升，同时也对登高平台的性能提出了更高的要求[1]。登高平台在调平作业过程中，工作平台载荷以及外界干扰等因素都会影响调平系统的动态性能和稳态精度。为了研究调平系统的特性，更好地制定控制策略，以满足登高平台调平系统对快速性、稳定性和可靠性的要求，本文建立了电液比例调平系统的数学模型，运用仿真软件MATLAB对登高平台电液比例调平系统进行仿真分析。

1 登高平台电液比例调平原理

登高平台电液比例调平系统原理图如图1所示，主要由电液比例换向阀、调平液压油缸、连杆机构、端部工作平台、角度传感器和控制器等组成。当登高平台底部举升机构带动登高平台做升降运动时，安装在工作平台上的角度传感器实时检测工作平台的倾角变化，通过控制器处理放大后作用于电液比例换向阀，控制阀芯的运动方向和开口度，从而控制调平油缸的运动方向及速度[2]。调平油缸通过小臂平行四边形连杆机构与工作平台相连，实现工作平台调平动作。

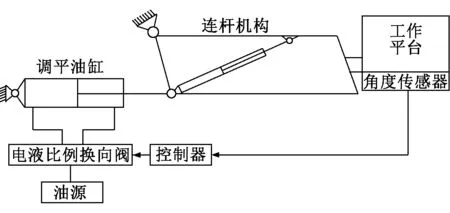
图1 登高平台电液比例调平系统原理图

2 登高平台调平系统仿真模型的建立

2.1 登高平台调平系统传递函数

登高平台电液比例调平液压系统为对称阀控非对称液压缸系统，为了便于分析研究，在推导建立调平系统数学模型过程中做如下假设[3]：①比例换向阀为理想零开口四边滑阀；②比例换向阀各节流口具有相同的流量系数；③不考虑液压管路对系统的影响；④液压缸为理想非对称单出杆缸；⑤忽略阀腔及管道内的压损；⑥不计负载弹簧刚度K的影响，即K=0。则电液比例换向阀传递函数为：

(1)

其中：xv为比例换向阀阀芯位移；I为输入电流；Ksv为比例换向阀增益；ωsv为比例换向阀固有频率；ζsv为比例换向阀阻尼比。

电液比例换向阀的流量方程线性化表达式为：

Ql=Kqxv-Kcpl.

(2)

其中：Kq为流量增益；Kc为流量-压力系数；pl为负载压力。

非对称液压缸的流量方程为：

(3)

其中：Q1为流入液压缸的流量，m3；Q2为流出液压缸的流量，m3；p1为液压缸进油压力，Pa；p2为液压缸回油压力，Pa；Cip为液压缸的内泄系数，m3·Pa/s；Cep为液压缸的外泄系数，m3/(s·Pa)；xp为液压缸活塞位移量，m；V1为液压缸无杆腔容积，m3；V2为液压缸有杆腔容积，m3；βe为油液有效体积弹性模数，Pa；A1为液压缸无杆腔活塞面积，m2；A2为液压缸有杆腔活塞面积，m2。

调平机构的力矩平衡方程为：

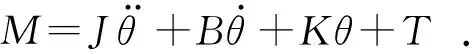
(4)

其中：J为转动惯量，kg·m2；B为负载黏性阻尼系数，Nm·s/rad；K为负载弹簧刚度，Nm/rad；T为负载阻力距，N·m；θ为工作平台转动角度。

将式(2)～式(4)联立，进行拉式变换，则调平系统传递函数可以简化为：

(5)

其中：f(θ)为转动力臂。

依据式(1)和式(5)并结合电液比例调平系统控制原理，得到调平系统传递函数方框图，如图2所示。系统仿真参数如表1所示。图2中，Ur、Ue分别为输入、输出程序；Uf为反馈信号；Ka为前置放大器增益。

图2 调平系统传递函数方框图

2.2 系统仿真模型

根据调平系统传递函数方框图及参数，在MATLAB/Simulink可视化仿真环境中建立登高平台电液比例调平系统仿真模型[4，5]，如图3所示。

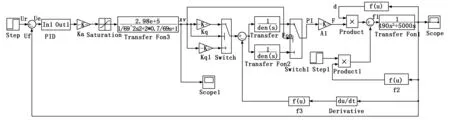
图3 调平系统MATLAB仿真模型

根据模糊自整定PID控制理论，建立系统模糊自整定PID控制系统仿真模型，如图4所示。设定偏差的量化因子Ke=32；偏差变化率的量化因子Kec=8；模糊控制器的输出增量ΔKp、ΔKi、ΔKd的比例因子分别为ap=0.8、ai=0.8、ad=0.08。模糊自整定PID控制器3个参数的初始值取Kp=18、Ki=6、Kd=0.5。

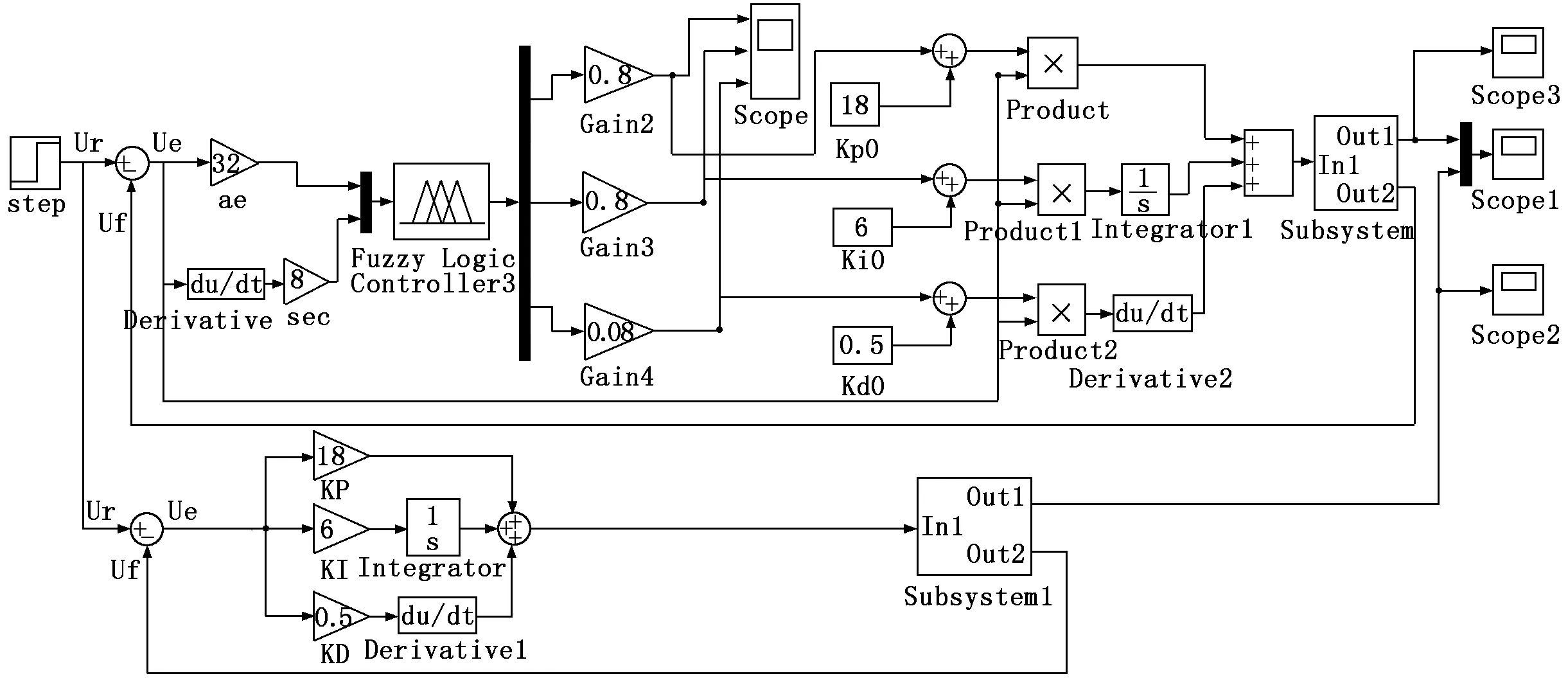
图4 模糊自整定PID仿真模型

3 调平系统仿真分析

针对登高平台在不同载荷下作业时通常出现工作平台跟踪响应慢，平台不能保持水平甚至出现工作平台在平衡位置附近反复抖动等情况，在仿真模型中对登高平台施加不同的工作载荷模拟负载工况，运用模糊自整定PID和常规PID两种不同的控制算法，分别进行仿真分析。调平系统在不同模拟载荷作用下的系统单位阶跃响应曲线如图5所示。

由图5可见，登高平台调平系统分别在模糊自整定PID和常规PID控制下，系统达到稳定状态的时间随着工作平台负载的增加都有所增加，在250 kg的载荷作用下，采用模糊自整定PID控制，调平系统达到稳定状态的时间小于0.4 s，而采用常规PID控制，调平系统达到稳定状态的时间超过2 s，调平系统响应滞后，调整时间较长，跟不上系统的响应速度，造成工作平台长时间处于倾斜状态；在空载状态下，采用模糊自整定PID控制，调平系统的动态响应速度更快，系统的超调量最大值控制在3%范围内，而采用常规PID控制，虽然系统的超调量很小，但是调平系统达到稳定状态的时间超过1 s，是模糊PID控制下的2倍以上。通过仿真分析可知，登高平台调平系统在不同负载模式下，通过模糊自整定PID控制，较常规PID控制可以获得更好的动态响应性能以及更好的静态稳定性能。

4 结论

通过建立仿真模型，模拟不同外负载进行仿真分析，结果表明登高平台调平系统模糊自整定PID控制算法能够实现控制参数的自整定，较常规PID控制算法能够获得更好的控制效果，特别适用于不同负载载荷工况下的系统调平控制。本文的论述对登高平台电比例调平系统及相关领域的研究及设计具有借鉴意义。