高压辊磨机机架强度及疲劳有限元分析*

张宪伟，王 勋，任云鹏

(1.沈阳盛世五寰科技有限公司，辽宁 沈阳 110168；2.沈阳建筑大学，辽宁 沈阳 110168)

0 引言

高压辊磨机是当今世界上最先进的物料粉碎设备，具有粉碎效率高、能源消耗低、适应能力强、土建投资少和生产环境好等优点，被广泛应用于水泥、矿山、冶金、化工等重要行业，成为目前粉磨系统的首选设备[1]。高压辊磨机的机架是其最主要的承力部件，既要承受辊子压碎物料所产生的反作用力以及液压缸拉力的联合作用[2]，又要承受这两种力所产生的力矩，受力情况复杂，因此需要其具备足够的强度。同时，所需破碎的物料呈现多样性、粒度大小不一、分布不均匀等特点[3]，辊子受力状态实时变化，在这些变化载荷的作用下，应力集中位置有疲劳断裂的风险，因此需要对其进行疲劳分析。

以往的高压辊磨机机架有限元强度计算只对机架单独进行分析，忽略了辊子及轴承的影响，同时也没有考虑物料的反作用力施加给机架的力矩，计算准确性严重欠缺。此外，以往的受力分析也仅考虑辊子挤压方向的一个作用力，因此无法准确分析机架强度，设计指导性不强。针对此问题，本文以高压辊磨机WGM240150为研究对象，运用有限元分析方法对其机架强度和疲劳特性进行仿真分析。

1 高压辊磨机结构及工作原理

本文所分析的WGM240150高压辊磨机结构如图1所示，其主要由给料系统、动力驱动系统、动辊系统、静辊系统、液压油缸及控制系统等组成。电机通过联轴器、减速器与安装在平行轨道上的静辊系统相连接。设备运行时，静辊及其机架固定在底座上不能移动，动辊及其机架能绕着其与底座相连接的销轴做小幅转动，动辊和静辊机架均由两个侧壁板、轴承座和扭力管组成，在顶部两个液压油缸的作用下，动辊及其机架向静辊方向摆动。其基本原理是利用层压粉碎理论，动辊辊子和静辊辊子共同对物料进行碾压破碎并将其挤压成密实的料饼。高压辊磨机电机启动后，在动力系统的驱动下辊子开始转动，两个挤压辊子以相同速度、相反方向转动。待加工物料通过给料系统输送到给料系统装置内。同时在顶部两个液压油缸的强大拉力作用下，动辊总成绕着其与底座相连的销轴转动，向静辊方向运动，两个辊子以相同速度、相反方向转动工作，物料受到两个辊子的碾压破碎并挤压成密实的料饼而从下部排出[4]。工作时，若破碎力过大，使得两个液压油缸的油压超出其最大限定值，则溢流阀溢流，从而起到对设备的保护作用。

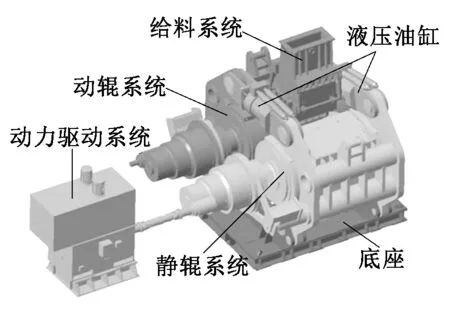
图1 高压辊磨机结构简图

2 高压辊磨机机架的强度仿真

高压辊磨机机架强度反映了其抵抗破坏的能力。辊磨机机架强度分析采用静力学分析方法，计算其在极限工况下、静力作用时的应力分布。

2.1 有限元模型的建立

动辊与静辊结构及受力基本相同，所以仅对其中之一进行分析。本文所建立的有限元模型包含机架、辊子以及调心轴承。调心轴承简化为外圈、内圈和滚动体，其中外圈与机架固定连接，忽略它们之间的过盈配合；内圈与辊子固定连接，忽略它们之间的间隙配合；滚动体与内、外圈均设置接触连接。模型处理删除了对计算有影响的圆角和倒角等，删除了对主体结构受力影响极小的轴套及轴承端盖等，以简化模型，提高计算精度。

划分网格是建立有限元模型前处理的最为重要的环节，它需要结合具体的工程问题，网格的形式对计算精度、计算规模和收敛性将产生直接影响[5]。为了保证网格的质量和计算的收敛性，网格划分全部采用solid45单元，该单元为低阶六面体单元，每个单元有8个节点，每个节点有x、y、z三个平动自由度，非常适用于线性和非线性的大形变。简化后机架及辊子的有限元模型如图2所示，仿真模型共有单元1 074 785个，全部为solid45实体单元。

2.2 边界条件的处理

WGM240150高压辊磨机在工作时可能会出现两种极限工况：一种是物料在辊子上均匀分布，两个液压油缸同时达到其拉力极限值，即均布极限载荷；另一种是物料集中作用在辊子的一端，两个液压油缸同时达到其拉力极限值，即极限偏载荷。在静力学强度分析中，依据选用油缸极限力大小和可能出现的极限工况，设置边界条件如下：

(1) 均布极限载荷：如图3所示，两个油缸作用力分别达到其极限力4 050 kN，动辊与物料接触处为线接触，约束其三个方向的线自由度，销孔内部节点约束4个自由度，放开其轴向平动及绕轴转动2个约束，摩擦因数设为0.3；销孔边缘节点约束5个自由度，放开其绕轴转动1个约束，摩擦因数设为0.3。

(2) 极限偏载荷：如图4所示，两个油缸作用力分别达到其极限力4 050 kN，动辊与物料接触处为点接触，约束其三个方向的线自由度，销孔内部节点约束4个自由度，放开其轴向平动及绕轴转动2个约束，摩擦因数设为0.3；销孔边缘节点约束5个自由度，放开其绕轴转动1个约束，摩擦因数设为0.3。

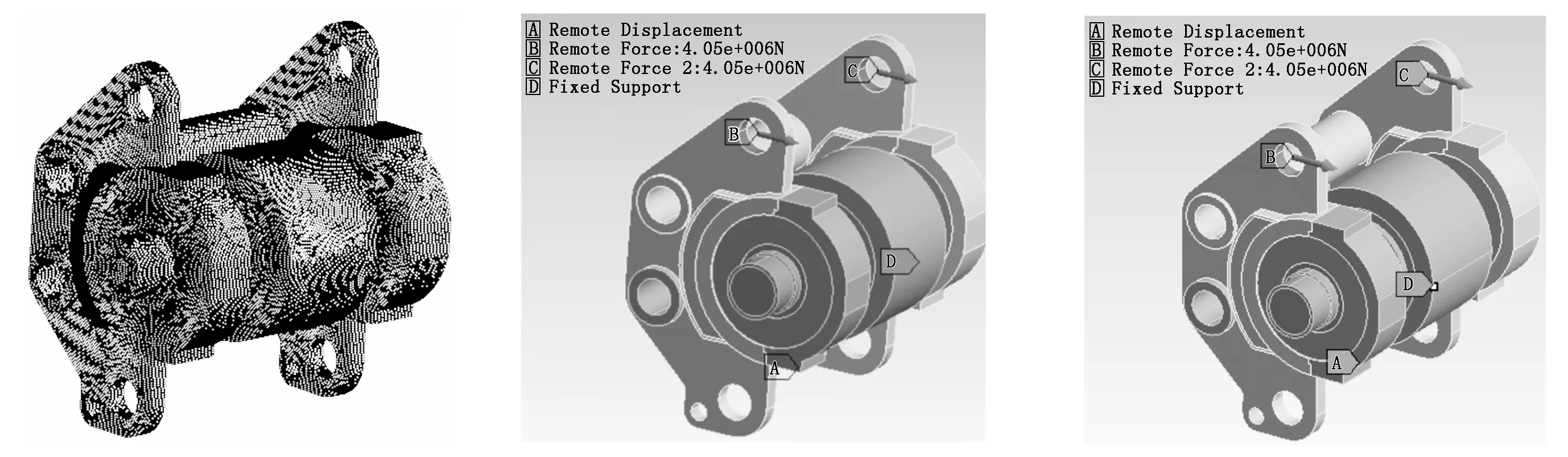
图2 机架及辊子的有限元模型 图3 动辊极限均布载荷边界条件 图4 动辊极限偏载荷边界条件

2.3 材料属性设置

机架钢板的主要材料为Q345B，相连接的扭力管材料为20g，相关的主要材料性能参数如表1所示。

表1 材料性能参数

2.4 辊磨机机架强度分析

辊磨机机架在两种极限工况下的Von-Mises应力分布分别如图5、图6所示。均布极限载荷工况下，机架大部分区域应力在43 MPa以下，机架存在应力集中点，位于侧壁板与轴承座过渡处，最大Von-Mises应力为238.51 MPa，但此应力集中是由于模型处理时去除此处圆角，导致此处截面突变所致，分析中对此数值无需关注；机架区域最大Von-Mises应力位置在侧壁板与轴承座过渡处，大小为89.298 MPa，远小于其屈服强度345 MPa，因此均布极限载荷作用下机架强度满足要求。极限偏载荷工况受力情况最为恶劣，但机架大部分区域应力仍在43 MPa以下，机架存在应力集中点，位置与均布极限载荷工况相同，应力集中点最大Von-Mises应力为381.25 MPa，但此应力集中点是由于模型处理时去除此处圆角过渡，导致此处截面突变所致，对此数值无需关注；机架区域最大Von-Mises应力位置在侧壁板与轴承座下部过渡处，偏向集中力一侧，大小为142.22 MPa，远小于其屈服强度345 MPa，因此极限偏载荷作用下机架强度满足使用要求。

由以上分析可知，WGM240150高压辊磨机在两种极限工况下，其大部分区域等效应力在43 MPa以下，最大等效应力为142.22 MPa，也远小于材料屈服强度。机架模型存在应力集中点，但这是模型简化处理所致。因此WGM240150高压辊磨机机架强度很大，满足使用要求，并存在一定的减重优化裕度。

3 高压辊磨机机架疲劳仿真

根据材料疲劳破坏前所经历的循环次数的不同，可以将其分为高周疲劳和低周疲劳，两种疲劳的主要区别在于塑性应变的程度不同。高周疲劳时，应力一般较低，材料处于弹性范围，因此其应力与应变是成正比的。低周疲劳则不然，其应力一般都超过屈服极限，产生了比较大的塑性变形，所以应力与应变不成正比。由前面的静力学仿真分析可知，机架在两种极限工况下工作时，塑性应变的程度不高，因此其疲劳分析属于高周疲劳范畴。

3.1 机架材料性能参数

Q345B的S-N曲线通常是通过成组实验的方法获得，即选取若干不同的应力范围水平，在每一应力范围水平下各取一组试件做实验，然后对各组实验数据分别进行统计分析，得到疲劳寿命的统计特征值，用曲线拟合疲劳寿命数据点得出Q345B的S-N曲线。选用材料Q345B的S-N曲线是在常温下20 Hz激励频率下多次测量得出。实验采用日本USF-2000型超声疲劳实验机在常温下进行，实验施加载荷为轴向拉压对称循环载荷，应力比R=-1，系统共振频率为20 kHz。经过拟合后得到Q345B的应力寿命特性曲线，如图7所示[6]。

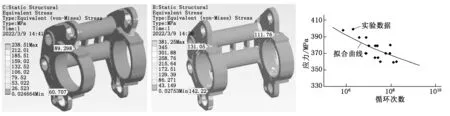
图5 均布极限载荷下 图6 极限偏载荷下 图7 Q345B的S-N拟合曲线机架的Von-Mises应力云图机架的Von-Mises应力云图

3.2 疲劳仿真分析

由分析和实测获得的载荷随时间历程可采用计数法、谱分析法等处理成用于结构疲劳寿命分析的载荷谱。由于辊磨机辊子载荷谱尚未经过测量，因此分析中假设其载荷谱为常幅谱。

在两种极限载荷工况下，由于载荷较大，辊磨机如果长时间处于极限工作状态，其机架可能会产生疲劳破坏。疲劳分析的边界条件与静力学分析相同，两种工况下的寿命云图分别如图8、图9所示。

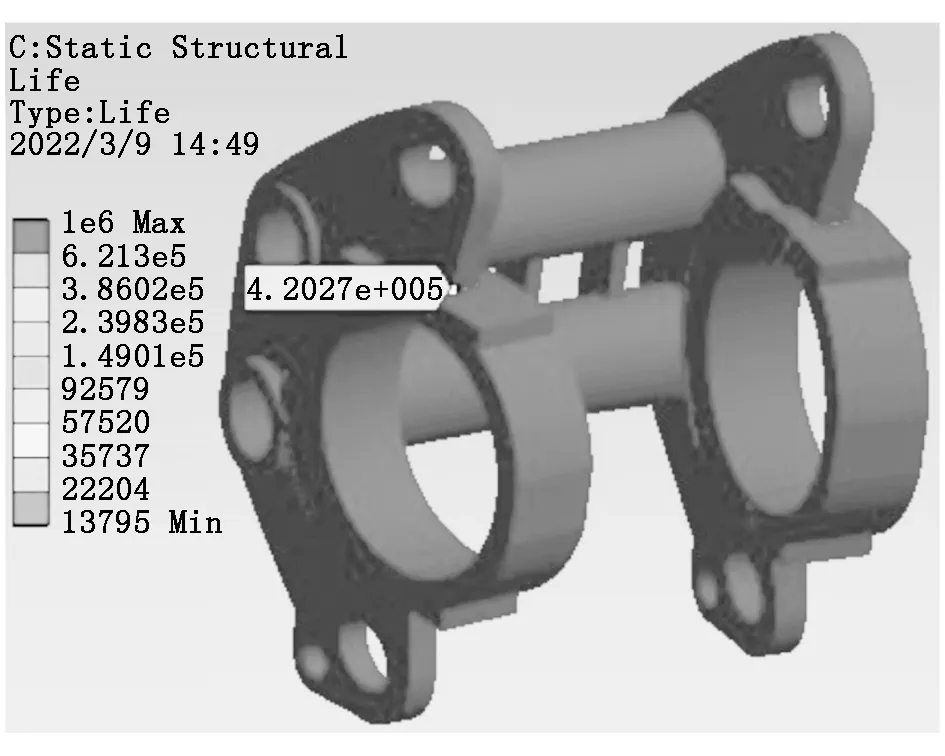
图8 机架均布极限载荷下的寿命云图

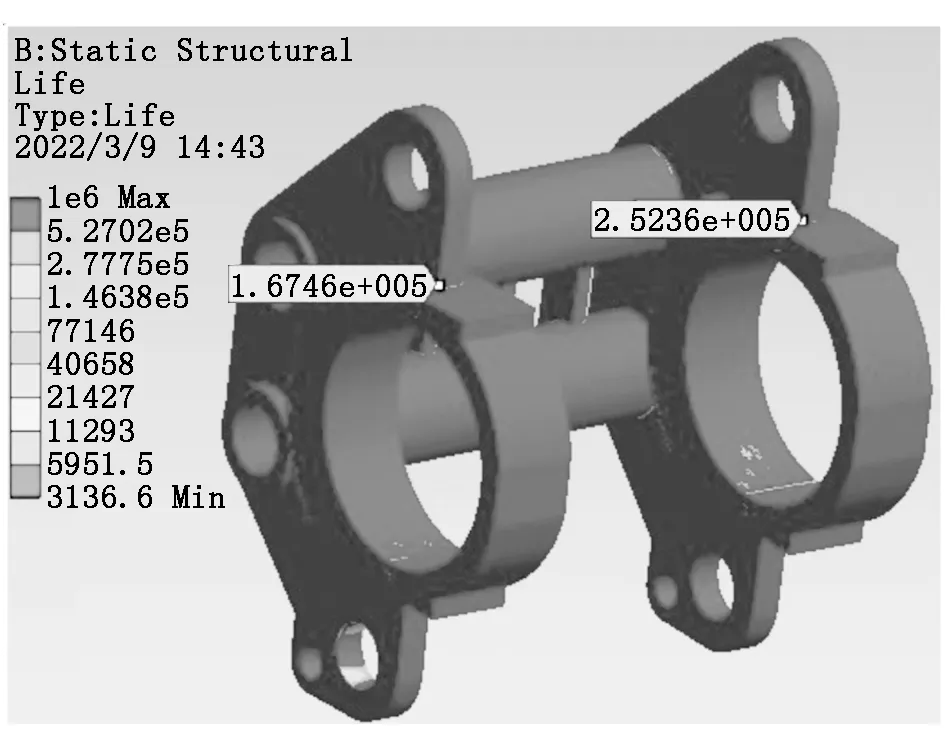
图9 机架极限偏载荷下的寿命云图

两种极限工况条件下，辊磨机机架的大部分区域的疲劳寿命都达到了106次，可以认为是无限寿命，不会出现疲劳破坏。最小寿命处位于轴承支座与机架侧壁板相接触的过渡处，因为此处截面有突变，存在应力集中点，这是由于模型简化处理时将此处的过渡圆角去除所致，因而此处计算结果不予考虑。最小寿命区域位于偏载一侧机架侧壁板与轴承座过渡处，循环次数约为1.674 6×105次，因此在设计中应保证此处有较大的过渡圆角。疲劳仿真分析结果表明，WGM240150高压辊磨机机架疲劳寿命满足使用要求，主体部分具有相当的减重优化空间。

4 结论

(1) 采用有限元分析方法，合理简化模型，正确施加边界条件，可以准确地分析辊磨机机架的强度和疲劳寿命，为辊磨机机架的设计与优化提供有效的计算依据。

(2) 通过有限元仿真分析可知，高压辊磨机WGM240150的机架强度很高，机架大部分区域疲劳寿命为永久，满足使用要求，且具有一定的减重裕度。机架两端轴承支座与机架侧壁板相接触位置应力较为集中，降低了机架的强度和使用寿命，设计中应保证此接合处有较大的过渡圆角。