具有时变通信延迟的多智能体系统改进蜂拥控制*

寇巧媛，袁 杰

(新疆大学电气工程学院，新疆 乌鲁木齐 830047)

1 引言

蜂拥行为是指大规模个体利用环境信息和简单规则实现群体行为的现象。近年来，多智能体的蜂拥行为引起了诸如生物、物理、社会科学、计算机科学和控制工程等许多领域研究人员的关注[1]。多智能体系统协同控制主要包括一致性研究和蜂拥控制[2,3]研究。1987年，Reynolds[4]提出了鸟群蜂拥行为模型，其中包含了分离、聚合和避免碰撞3条基本规则。在Reynolds模型的基础上，多种基于理想条件的蜂拥控制算法被相继提出[5,6]。这些算法较好地实现了多智能体的位置一致和速度趋同。但是，由于多智能体系统本身具有非线性、网络拓扑切换特性和通信延迟等问题[7]，容易使协同现象退化甚至造成系统不稳定。因此，越来越多的研究人员将目光投向解决多智能体系统的实际应用上[8]。文献[9]研究了具有有向固定拓扑图上的高阶不确定非线性多智能体系统一致性问题。文献[10]利用拉普拉斯矩阵的性质和改进的包含控制，将一般线性多智能体系统控制问题转化为离散时间线性切换系统的稳定性问题。文献[11]研究了定向交互拓扑下分数阶多智能体系统的分布式控制，提出了具有绝对阻尼和通信时延的控制规律。文献[12]考虑了具有非周期性间歇通信拓扑的线性多智能体系统的一致性，利用两跳邻居信息设计了间歇通信拓扑控制规律。文献[13]利用人工势函数和状态观测器设计控制方案，解决具有外部干扰的多智能体系统蜂拥问题。动态多智能体系统的通信时延问题已经引起了许多研究人员的关注[14,15]。文献[16]研究了复杂环境下固定通信时延多智能体的蜂拥控制。文献[17]研究了具有通信时延的多智能体系统的蜂拥控制问题，其只考虑了速度信息的时滞，并没有考虑位置信息的时滞。

当网络结构不连通时，系统将具有不同的网络延迟[17]。因此在实际应用中，不仅要考虑网络信息阻塞引起的未知通信时延，还要考虑异构拓扑造成的时延。此外，在目前诸多研究中，通信时延上限均作为已知条件使用，尚未有研究人员研究在复杂环境中存在时变通信时延的不确定非线性二阶多智能体系统的蜂拥控制。

针对上述问题，本文在具有时变通信时延的不确定非线性二阶多智能体系统中利用鲁棒自适应算法设计了满足速度匹配和位置跟随的控制规律，使多智能体系统实现蜂拥行为；同时利用Lyapunov-Krasovskii方法构造能量函数，证明了采用本文提出的控制规律能确保多智能体系统网络始终连通，群体速度收敛于虚拟领导者的速度，智能体之间不会发生碰撞，并且当通信延迟满足一定要求时多智能体系统趋于稳定；最后通过实验验证了本文设计的鲁棒自适应算法能够实现二阶多智能体系统的蜂拥控制，在保证位置跟随和速度匹配的同时，增强了二阶多智能体系统的抗干扰能力。

2 预备知识

2.1 基本定义

令R,R+,Rd,RN×N分别代表一维实空间、一维正实空间、d维实向量和N×N维实矩阵。Id表示d维的单位矩阵。r表示智能体的传感器半径，R表示智能体的交互半径，‖·‖1表示1范数，‖·‖表示2范数，即欧氏距离。

2.2 图论知识

3 控制规律设计和稳定性证明

3.1 不确定非线性二阶多智能体系统运动学模型

在d维噪声环境中，由N个节点组成的二阶多智能体系统包含了一个虚拟领导者(运动学模型中下标为0)和N-1个智能体(运动学模型中下标为1,2,…,N-1)。第i个智能体运动学模型描述如式(1)所示：

(1)

其中,初始值表示如式(2)所示:

(qi,pi)(0)=:(qi0,pi0),i=1,…,N-1

(2)

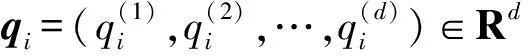
(3)

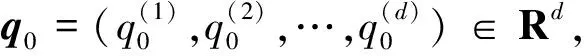
非线性动力学函数f(·)和扰动φ(·)满足局部Lipschitz连续条件[16]，即对于所有的p1(t)，p2(t)∈Rd且θ,γ为非负常数,满足式(4)：

(4)

假设1初始G(0)是连通图。

假设2虚拟领导者的控制规律输入是有界的，即∃κ>0，使得‖f(p0(t))+φ(p0(t))‖<κ<∞。

3.2 控制规律设计

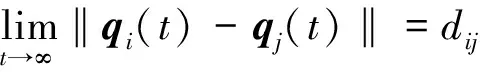
ui(t,τ(t))=u1i+u2i+u3i+u4i

(5)

(6)

u1i为人工势函数,采用文献[19]的定义，如式(7)所示：

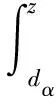
(7)

其中,

(8)

(9)

(10)

其中,h∈(0,1),ω>0,ψα(z)满足式(11):

▽qiψα(‖qij(t)‖σ)=▽qijψα(‖qij(t)‖σ)=

-▽qjψα(‖qij(t)‖σ)

(11)

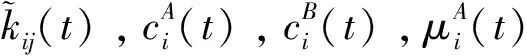
i,j=1,2,…,N-1

(12)

其中,βij,mi,ni,li,ηi为任意正实数，各个参数初始值设定如式(13)所示：

(13)

3.3 稳定性证明与分析

定理1考虑具有时变通信延迟的不确定非线性二阶多智能体系统的运动学模型如式(1)和式(3)所示，输入控制如式(5)和式(6)所示，人工势函数如式(7)所示，假设1至假设3成立，初始能量Q0是一个有限值，则有以下结论成立：

(1)当t≥0时，多智能体系统网络图G(t)满足连通性。

(3)智能体之间不会发生碰撞。

(14)

证明一般地，在tk时刻，图G(0)切换到图G(k)。令t(0)=0，在t∈[t(0),tk)根据Lyapunov-Krasovskii方法构造能量函数Q(t)如式(15)所示(具体推导过程见附录)：

(15)

Q(t)对时间t求导，且根据假设1和young不等式[15]：2xTy≤xTPx+yTP-1y可得到式(16):

(16)

对于任意x∈Rd，满足不等式‖x‖≤‖x‖1[20]，可得式(17)和式(18):

(17)

(18)

Q(t+tk)≤Q0+mψ(‖qij(t)‖α)≤Qmax

(19)

□

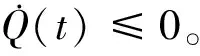
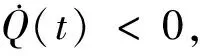
4 仿真分析

利用控制规律式(5)和式(6)得到的三维轨迹以及不同迭代次数下智能体位置、速度如图1示。从图1可以看出，在多智能体系统移动过程中智能体之间能够形成紧密的晶格状网络；智能体之间保持强连通和集群构型的稳定；各个智能体的速度方向和大小趋于一致，并与虚拟领导者保持同步；各个智能体位置趋于虚拟领导者位置。

图2为Laplacian矩阵特征值和各参数调节图。其中,图2b～图2f展示了鲁棒自适应控制算法调节各个参数的变化情况，可以看出当迭代次数达到200时，多智能体系统中各个参数趋于平稳，根据鲁棒自适应参数的定义可知，此时系统集群和跟随情况已经趋于稳定和收敛。图1所示的多智能体系统的运动轨迹和不同参数下智能体的位置和速度，表明对应时刻的智能体之间已经形成稳定的晶格状构型，智能体速度与虚拟领导者速度达成同步，群体中心位置收敛于虚拟领导者位置，这与鲁棒自适应参数曲线相一致。图2a中Laplacian矩阵特征值随时间变化的情况也证实了随着时间t的推移，多智能体系统的网络一直保持强连通。

为了检验本文所提出的控制规律对外界未知干扰和时变通信时延的鲁棒性，分别选取不同信号干扰强度ξ和时变通信时延强度参数τm进行对比实验。考虑时间对系统时滞的影响，选取τ(2)=τme-5tsin2(t)作为多智能体系统的时变通信时延函数。设定时变通信时延调节参数τm为0.1，0.2，0.3，0.4，0.5。在不同强度通信时延下分别进行100次实验，系统速度误差ε小于0.02时认为控制规律收敛。实验结果如图3和表1所示，其中图3a和图3b验证了多智能体系统在不同强度的时变通信延迟下网络系统能够快速收敛，并且智能体与虚拟领导者的速度误差不断减少，同时各智能体相对虚拟领导者的位置保持稳定。表1表明时变通信时延的强度并不影响系统的收敛速度。

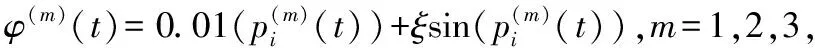
Table 1 Convergence time of system error

5 结束语

本文提出具有时变通信时延的多智能体系统的鲁棒自适应蜂拥控制规律，并对自带不确定非线性二阶多智能体系统模型进行验证，通过仿真实验得出以下结论:在外界干扰和通信时延同时存在时，动态多智能体系统可以保持较好的晶格状网络，维持较强的连通性，智能体的位置和速度都收敛于虚拟领导者。当时变通信时延满足一定条件时，鲁棒自适应蜂拥控制规律可使多智能体系统收敛并达到稳定。在不同强度干扰下，系统可快速收敛并形成稳定的拓扑结构。因此，采用鲁棒自适应设计的蜂拥控制规律可使系统具有较强的适应能力和鲁棒特性。然而，多智能体系统在通信时延下选取关键子网节点还没有明确的控制设计方案，如何利用复杂网络特性设计蜂拥控制方案，以提高多智能系统信息传递效率是下一步研究重点。

Q(t)=Qi1(t)+Qi2(t)+Qi3(t)+Qi4(t)=

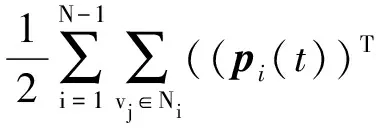
(pj(t))T∇qij(t)ψα(‖qij(t)‖σ))=

(pj(t))T∇qjψα(‖qij(t)‖σ))=

(pj(t))T∇qiψα(‖qij(t)‖σ))=

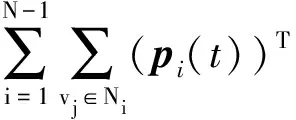
f(p0(t))-φ(p0(t)))=

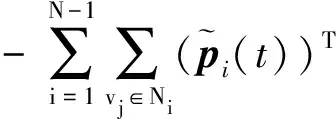
f(p0(t))-φ(p0(t)))

对于任意x∈Rd，满足不等式‖x‖≤‖x‖1[19]，可得:

根据young不等式[18]：2xTy≤xTPx+yTP-1y可得到: