非结构有限体积CFD计算的网格重排序优化*
张 勇,张 曦,万云博,何先耀,赵 钟,卢宇彤
(1.中国空气动力研究与发展中心计算空气动力研究所,四川 绵阳 621000;2.中山大学计算机学院,广东 广州 510006)
1 引言
计算流体力学CFD(Computational Fluid Dynamics)通过计算机数值求解流体力学控制方程以获得流动信息。随着高性能计算HPC(High Performance Computing)硬件的快速发展,CFD在工业装备建设中得到了越来越多的应用。
CFD通过计算网格离散空间,早期主要采用结构网格。随着几何外形复杂性和保真度的增加,结构网格生成在整个模拟周期中占据了绝大部分时间。非结构网格具有自动化程度高的优点,能够更好地适应诸如飞行器、旋转机械等复杂几何外形,在大气海洋、航空航天等许多科学计算领域运用广泛。由此发展了众多数值模拟软件,例如,基于有限体积方法的 OpenFOAM(Open Field Operation And Manipulation)[1]、FUN3D(Fully Unstructured Navier-stokes three-Dimensional)[2]、SU2(Stanford University Unstructured code)[3],基于有限元方法的Fludity[4]和MOOSE(Multiphysics Object Oriented Simulation Environment)[5],基于通量修正方法的pyFR(Python based Flux Reconstruction)[6]等。然而,由于非结构网格数据存储不规则,数据只能间接访问[7],增大了访存延迟,对非结构网格计算效率造成了不利影响。随着高性能计算技术的发展,科学计算进入“E级”时代,通用图形加速器GPGPU(General Purpose Graphics Processing Unit)凭借其计算能力强、功耗低的优点,在科学计算中得到了越来越多的应用。GPU的访存模式[8]放大了非结构网格不规则访存带来的延迟,如何提高非结构网格的数据局部性,充分利用CPU和GPU的计算性能,提高非结构网格有限体积数值模拟的计算性能,已经成为高性能计算领域的重要课题之一。
提高非结构网格的数据局部性有许多方法。一些研究人员对非结构网格的数据存储布局进行了研究[9],但无论是AOS(Array Of Structure)还是SOA(Structure Of Array)的存储布局都避免不了数据的间接访存。Weng等[10]通过调整循环模式改进数据局部性,但是该方法只优化了部分计算热点,无法实现全局性优化。
网格重排序是一类能有效提高数据局部性的方法,通过对网格几何拓扑如体、面、点的编号重排,改变数据访问顺序,减少访存延迟。Lohner[11]针对有限元方法提出了若干重排序的方法。Andrew等[12]通过一种线排序方法,重排体和面编号,提升了高阶DG(Discontinuous Galerkin)方法计算Euler方程的性能。Lani等[13]在有限体积方法中使用了RCM(Reverse Cuthill-Mckee)方法,但是性能改善有限。目前,大多数文献都是对网格重排序在CPU或GPU等单一类型硬件上的性能影响展开研究,缺乏对CPU、GPU等不同硬件类型的统一性研究。
本文根据非结构网格有限体积CFD计算的特点,基于风雷软件提出了一种网格重排序策略,以优化数据局部性。首先,简述了非结构有限体积CFD的理论方法和所采用的计算程序;然后,给出了本文所提出的网格重排序方法,并采用典型算例分析了该方法在CPU和GPU上的数值计算结果。
2 理论基础与计算程序
本文研究基于开源CFD软件“风雷(PHengLEI)”[14-18]。风雷软件是中国空气动力研究与发展中心研发的面向流体工程的混合CFD平台,面向全国开源(https://osredm.com/)。风雷软件是全球首款能同时支持结构网格(算法)和非结构网格(算法)的CFD软件,也是同时支持有限体积和有限差分方法的“混合”计算平台。本节简要介绍本文研究涉及到的理论基础,包括控制方程与数值方法、网格几何拓扑。
2.1 控制方程与数值方法
NS(Navier-Stokes)流动控制方程积分形式可以表示如式(1)所示:
(1)
其中,Fc和Fv分别表示对流通量和粘性通量(下标c代表对流相关项,下标v代表粘性相关项);Q表示包含守恒形式的流动矢量,可以表示如式(2)所示:
(2)
其中,ρ、u、v、w和E分别表示流体密度、速度在x、y、z这3个方向的分量及单位质量总能量。采用格心式有限体积方法,将这些流场变量定义在控制体(Control Volume)单元Ω中心上。
有限体积方法将物理空间划分为许多小的控制体(Volume);体的边界称为面(Face)。相应地,NS方程可以表示如式(3)所示:
(3)
其中,Ωvol表示控制体的体积;控制体拥有NF个面,第m个面的面积为|Sm|;对流通量Fc采用Roe格式计算,通过采用限制器抑制流场间断产生的数值振荡;粘性通量Fv采用中心格式计算;湍流模型采用Splart-Allmaras一方程模型;时间推进采用Runge-Kutta显式和LU-SGS(Lower Upper-Symmetric Gauss Seidel)隐式方法。程序的具体算法参见文献[14-18],在一个时间步的流程如图 1所示。
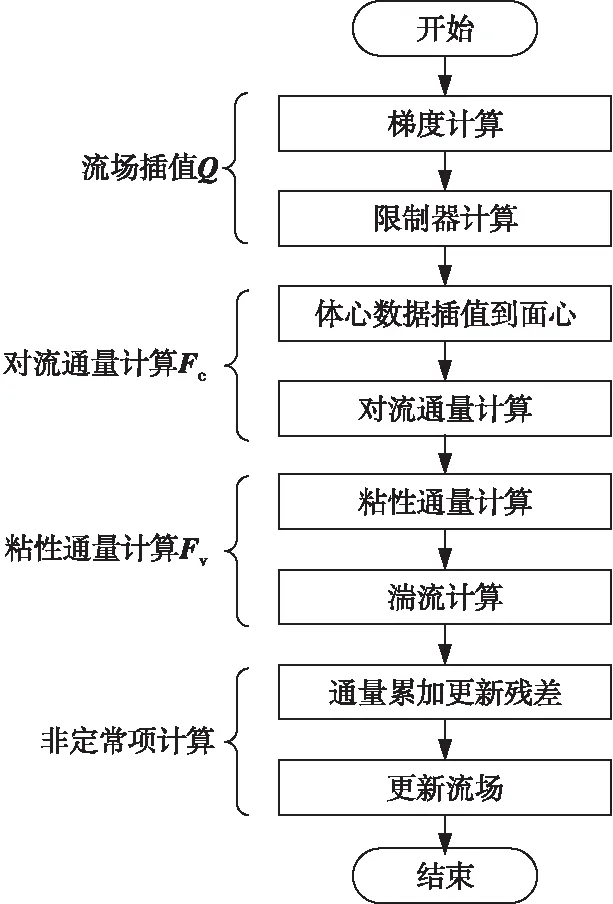
Figure 1 Flow chart of program in one time step
2.2 网格几何拓扑
非结构网格存储没有结构网格那样规律,其点、面、体(单元)编号都是无规律存储。在非结构网格几何拓扑关系中,面和体之间的连接关系尤为重要,广泛应用于各类通量计算中,其具体关系通过面编号和体编号来表示。对于格心型有限体积方法,体(Volume)即是计算单元本身,下同。
对于面编号,在风雷软件中,每个面两侧有且仅有2个体,分别为左、右单元。左和右的定义是相对的,软件中规定面法向所指向的体为右侧体,另一侧为左侧体,即面法向从左体指向右体。为编程方便,将面分为边界面和内部面2种类型,数组中先存储边界面,再存储内部面。对于内部面,其左、右单元都是内部单元;对于边界面,左单元为内部单元,右单元是左单元以边界面为对称的镜像虚拟单元。
面法向采用叉乘计算得到。如图 2所示,A=P3-P1、B=P2-P1分别是2个矢量,二者构成一个平面。根据线性代数,其单位法向的计算表达式如式(4)所示:
(4)
对于任意凸多边形的法向量,可以将每条边与面心连接形成若干子三角形,将各子三角形的法向量以各自面积加权得到多边形的法向量。
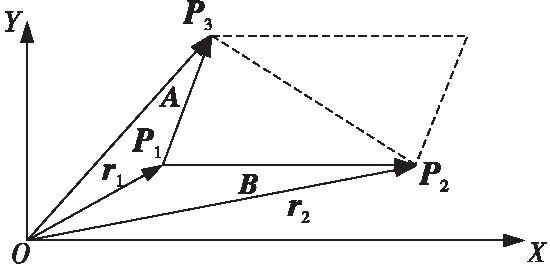
Figure 2 Diagram of plane normal vector calculation
采用2个数组存储左、右体编号。如图 3所示,编号为O和P的2个体都包含编号为f2的面,若规定面的右单元体编号存储在cellRight数组中,且面的另一侧体编号存储在cellLeft数组中,则可通过数组直接得到左、右体编号,即cellRight[f2]=P,cellLeft[f2]=O。
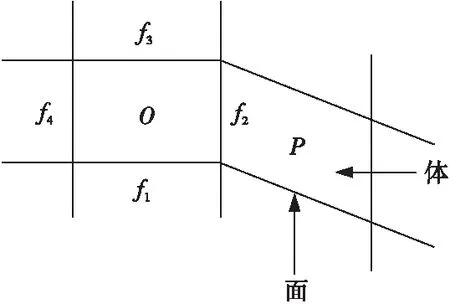
Figure 3 Geometry topology: volume and face
变量ρ、u、v、w、p等存储在体中心,称为体数据(Volume Data);对流通量Fc和粘性通量Fv等变量存储在面中心,称为面数据(Face Data)。体数据和面数据由各自的编号索引,并以SOA方式存储。体数据可以由体编号直接索引,也可以由面编号间接索引。例如,表示残差的体数据Res,其体编号为O,可以通过体索引Res[O]或者面索引Res[cellLeft[f2]]2种方式得到。风雷软件中面、体在数组中存储的顺序分别如图4和图5所示。

Figure 4 Numbering order of face

Figure 5 Numbering order of volume
图4和图5中,nCell是内部体总数,nTotalCell表示内部体和虚拟体数量之和,nBoundFace表示边界面的数量或者虚拟体的数量,nTotalFace表示内场面和边界面数量之和。体编号在[0,nCell),虚拟体编号在[nCell,nCell+nBoundFace),从内部体编号尾部开始逐一编号,定义第iFace个边界面所对应的虚拟体编号为iFace+nCell。
3 网格重排序方法
网格重排序分为两部分:体网格按照RCM(Reverse Cuthill-Mckee)方法进行重排,面网格以网格体为单位重新排列。下面分别说明。
3.1 RCM体重排序
RCM方法[19]采用近邻排序的方法,以保证网格编号在空间中相对集中分布,从而使得体数据存储时在内场空间更紧密。通过RCM方法,反映网格邻接关系的矩阵带宽会减小。如图 6所示,比较了29万网格规模下体网格排序前、后的矩阵结构,可以发现体编号重排序使得邻接矩阵非零项更加紧凑。

Figure 6 Comparison of matrix structures with and without volume reordering
3.2 面重排序
本文设计了一种面重排序算法,针对风雷程序的内部面,以体网格拥有的面为基本单位,按照体网格内原始的编号顺序,为内部面重新排序。这样可以缓解边界面编号造成的内部面编号不连续问题,提高边界数据访存效率。具体算法如算法1所述。
算法1面编号排序算法
输入:体-面拓扑关系offsetCellFace、numFaceOfCell和cellFace。
输出:排序前、后面编号映射关系mapFace,排序后的几何拓扑关系。
第1步升序排列cellFace中每个体网格对应的面编号;
第2步初始化数组mapFace={-1};
第3步初始化面编号计数器labelFace=nBoundFace-1;
第4步遍历体网格,重排面编号:
FORcellID=0 TOnTotalCell-1
获取体网格cellID在cellFace的偏移量offset=offsetCellFace[cellID];
获取体网格cellID在cellFace中存储的面编号数量numFaces=numFaceOfCell[cellID];
遍历组成体网格cellID的全部面:
FORfaceInCell=0 TOnumFaces-1
获取面编号faceID=cellFace[offset+faceInCell];
IF(面faceID是内部面)&&(面faceID映射关系仍未改变)THEN
编号计数器labelFace累加1;
更新faceID的映射关系:
mapFace[faceID]=labelFace;
ENDIF
ENDFOR
ENDFOR
第5步采用mapFace更新网格几何拓扑关系。
该算法首先将cellFace中以体网格为单位存储的面编号按照升序排列(第1步);然后初始化映射数组mapFace和编号计数器labelFace(第2、3步),编号计数器从nBoundFace-1开始,只对内部面编号;以网格体为单位,通过2层嵌套循环遍历cellFace中的所有面编号(第4步);对于内部面,更新编号计数器,并将该值赋给映射数组(第2层循环);网格拓扑相关的变量,例如cellFace等,根据映射数组更新(第5步)。
4 算例测试与分析
4.1 算例、计算环境和测试方法
为分析网格重排序对非结构网格有限体积CFD计算的结果影响和优化效果,采用5套不同规模的ONERA M6机翼外流场三维非结构网格作为测试集。如图 7所示,ONERA M6机翼三维非结构网格由三棱柱和四面体组成,其中,三棱柱分布在物面附近的边界层区域,四面体用于填充剩余计算域。5套网格的单元数如表 1所示。
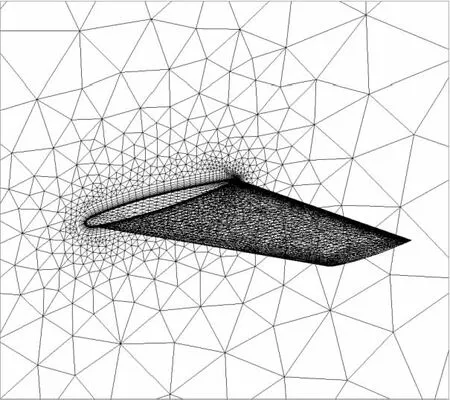
Figure 7 ONERA M6 Mesh
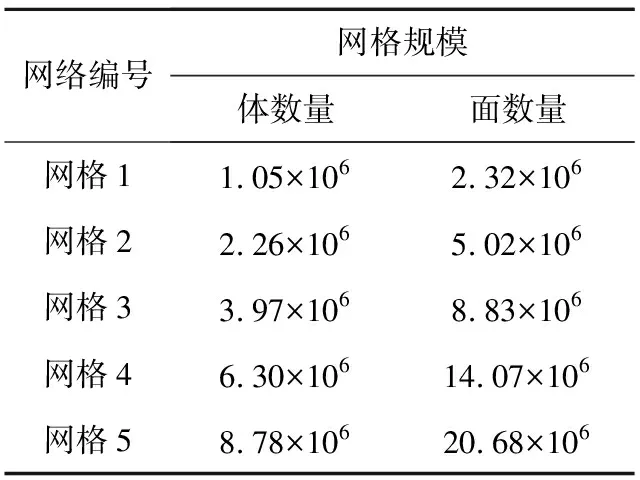
Table 1 5 different meshes
测试采用风雷软件非结构求解器GPU并行开源版本,该版本程序可在红山开源平台申请下载(https://forge.osredm.com/projects/p68217053/PHengLEI/tree/Branch_TH)。采用的硬件环境为:基于CUDA 10.0[20]驱动的NVIDIA Tesla V100 GPU,Intel Xeon E5-2692 CPU。
本文的GPU并行优化的前提是网格重排序,理论上网格重排序只影响计算效率,不影响计算的收敛结果。对此,首先对比分析网格重排序对显式计算和隐式计算的影响。
4.2 网格重排序对计算结果的影响
4.2.1 对隐式LU-SGS方法的影响
LU-SGS方法数据依赖性强,对计算顺序较敏感,本节讨论网格重排序对隐式计算LU-SGS方法的影响。
图 8给出了400万网格规模(网格3)下平均残差averageRes(NS方程未知数在相邻时间步二阶范数的平均值)随迭代步变化的曲线。可以看到,网格编号排序前后残差收敛值趋于一致,且重排序的收敛效果优于未排序时的。
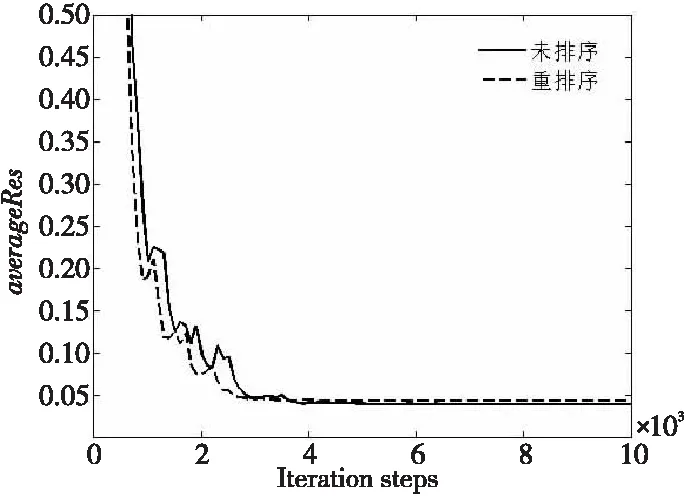
Figure 8 Variantion curves of residual error before and after mesh reordering under 4 million grid scale
不同网格规模下1万步处的平均残差比较如表 2所示。可见,随着网格规模的不断增大,重排序的计算平均残差逐渐减小。与未排序相比,其加速收敛的效果更加明显。
不同网格规模下,网格重排序对空气动力学系数的影响如表3所示。由表3可知,网格重排序对升力系数的影响在0.24%之内,对阻力系数的影响在0.5%之内,二者均在气动计算可接受的误差之内,可认为重排序不影响计算结果。

Table 3 Relative error of aerodynamic coefficients at 10 000 steps for reordering and unordering
综上,由于LU-SGS方法数据依赖性较强,体网格编号重排改变了计算顺序,提高了数据局部性,在一定程度上改善了求解过程的收敛效果,但对隐式方法的计算结果无明显影响。
4.2.2 对显式Runge-Kutta方法的影响
本节讨论网格重排序对显式计算Multi-Stage Runge-Kutta方法的影响。
图 9给出了40万网格规模下平均残差随迭代步变化的曲线。可以看出,6万步后残差曲线收敛,未排序和重排序的平均残差收敛曲线没有明显差异。从图 10中未排序与重排序平均残差的插值可以看出二者平均残差是相同的。

Table 2 Comparison of residual values at 10 000 steps for reordering and unordering
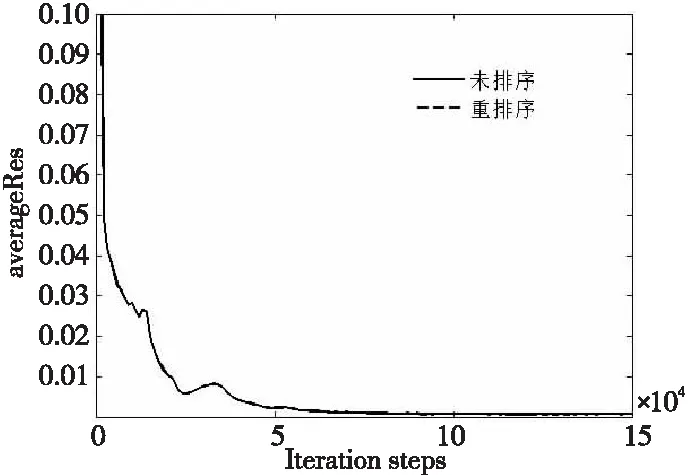
Figure 9 Variantion curves of residual error before and after mesh reordering under 400 000 gride scale
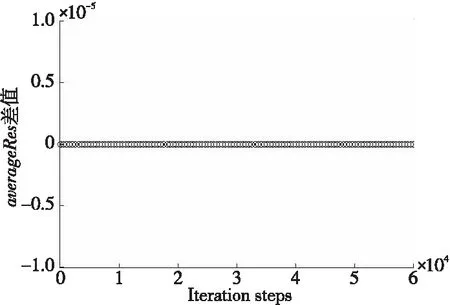
Figure 10 Difference of average residual values before and after mesh reordering
可见,网格重排序对显式计算的结果完全没有影响,这是因为:显式方法计算时,每个网格只和局部几何拓扑有关,网格重排序虽然改变了体网格、面网格的编号顺序,但是并没有改变几何拓扑结构,不会影响计算结果。
4.3 CFD程序性能分析
从4.2节分析可见,网格重排序不会影响计算结果,说明针对GPU并行算法改造是可行的。本节分别就CPU和GPU上的计算来分析影响计算效率的热点。
对于显式计算,在CPU计算时,发现耗时较大的前8个热点F0~F7函数占据了总计算时间的近70%,如图 11a所示。在GPU计算时,发现耗时较大的前8个热点K0~K7也占据了总计算时间的70%。
对于隐式计算,在CPU计算时,前8个热点函数FI0~FI7占据了运行总时间的一半以上。
4.3.1 网格重排序对于CPU计算性能的影响
在CPU上,网格重排序对显式计算和隐式计算的运行时间都会产生影响。本节分别讨论网格重排序对显式计算和隐式计算在不同网格规模下运行时间的影响。在Intel Xeon E5-2692上记录的运行时间。
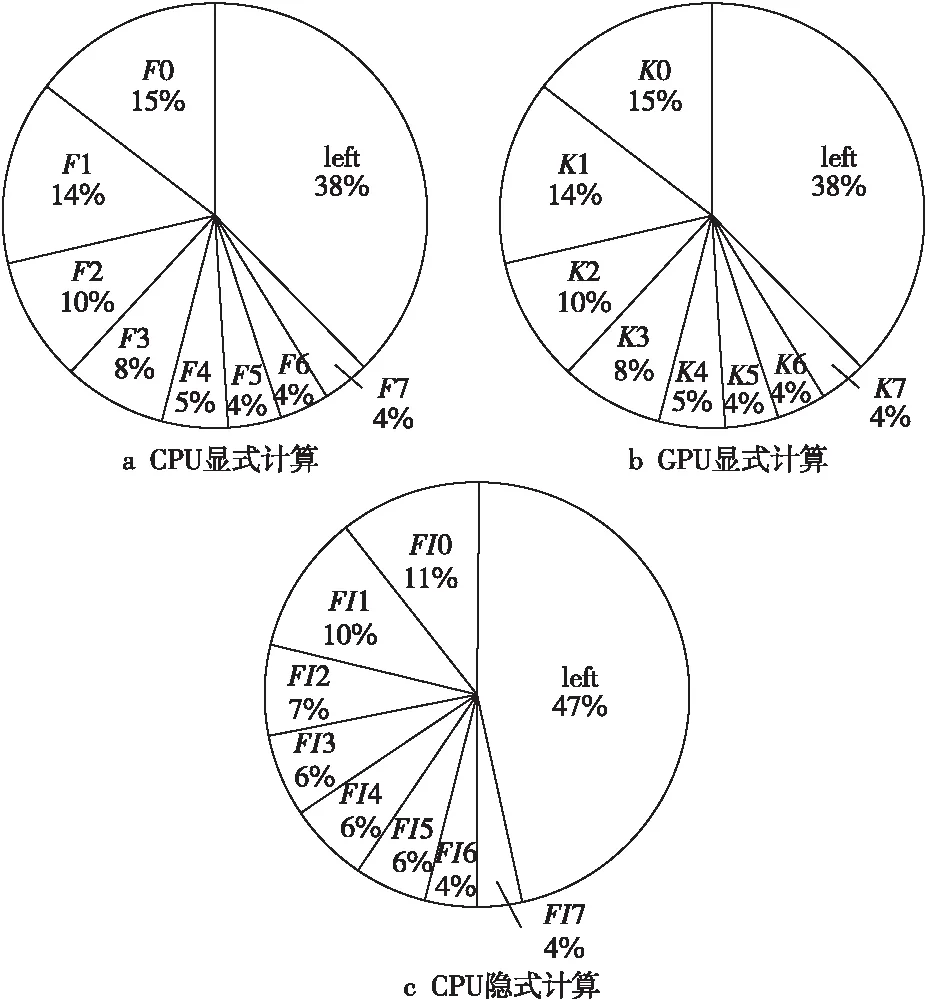
Figure 11 Hot spot functions and kernels of explicit computing and implicit computing on CPU and GPU
表4是网格3(400万网格)规模下网格排序前、后热点函数的运行时间。以未排序的函数运行时间作为分母,对运行时间无因次化,结果如图 12所示。可见,大部分函数的运行时间在重排序的网格下缩短了10%~40%。

Table 4 Comparison of hot functions’ explicit executing time before and after mesh reordering
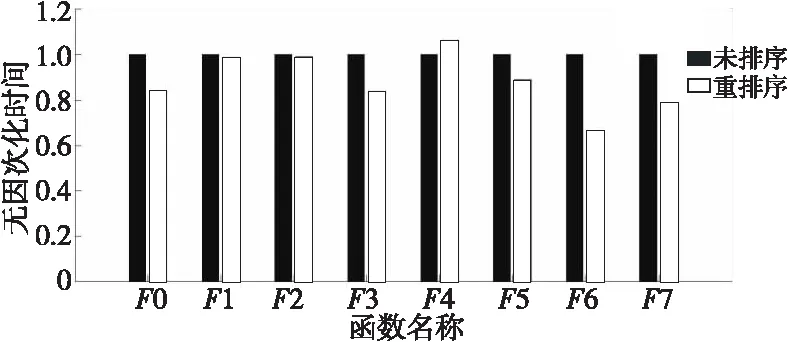
Figure 12 Comparison of hot spot functions’ explicit executing time before and after mesh reordering
针对不同网格规模下的显式计算,记录了24进程并行计算的运行时间,结果如表 5所示。
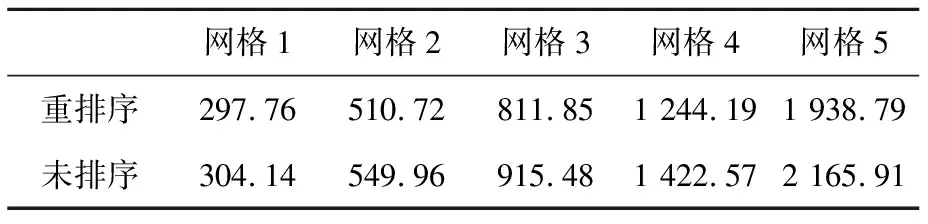
Table 5 Executing time of explicit computing before and after mesh reordering
对未排序运行时间作无因次化处理,重排序、未排序显式计算的运行时间如图 13所示。网格重排序缩短了显式计算在所有网格规模下的运行时间,随着网格规模扩大,重排序能够节省15%~20%的运行时间。
重排序改变了数据在内存中的分布,增强了局部性,提高了Cache命中率,减小了访存延迟。特别是在网格规模较大的时候,内存读取次数增多,能够节省更多的运行时间。
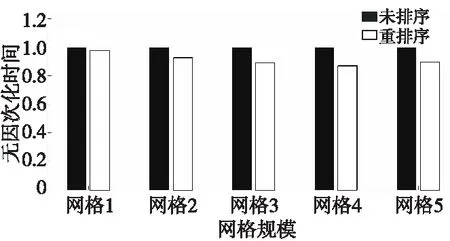
Figure 13 Comparison of explicit parallel computing’s executing time before and after mesh reordering on CPU
表6统计了CPU隐式计算在网格3上的热点函数网格重排序前、后的运行时间。通过图 14可知,网格重排序可以使部分热点函数的CPU运行时间缩短。FI0梯度计算的最明显,运行时间缩短了大约17%;LU-SGS部分相关的FI3和FI4运行时间缩短了10%以上。
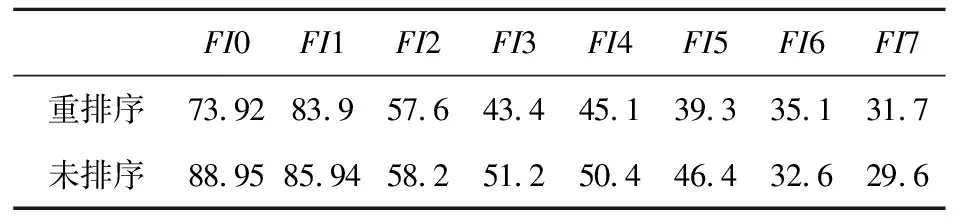
Table 6 Comparison of hot spot functions’ implicit executing time before and after mesh reordering on CPU
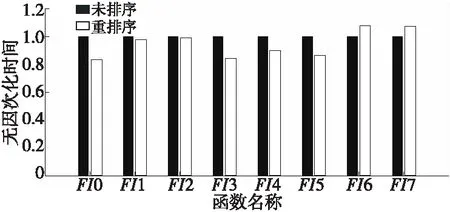
Figure 14 Comparison of hot spot functions’ implicit executing time before and after mesh reordering on CPU
本文也对网格重排序对隐式计算的影响进行了评估。针对隐式计算,开展了不同规模的并行计算。记录时间如表 7所示。
对未排序运行时间作无因次化处理,重排序、未排序隐式计算的运行时间如图 15所示。对于隐式计算,网格重排序仍然能够使缩短运行时间。

Table 7 Comparison of implicit parallel computing’s executing time before and after mesh reordering on CPU
对于规模较小的网格1(100万体网格),运行时间缩短接近10%,比显式计算的优化效果更明显。这可能是由于体网格排序对于矩阵求解的优化即使在网格规模较小的时候仍然起作用。随着网格规模增大,重排序效果也更加明显,在网格4规模下,重排序减少了将近20%的运行时间。
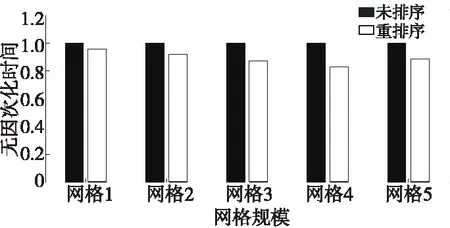
Figure 15 Comparison of implicit parallel computing’s executing time before and after mesh reordering on CPU
4.3.2 网格重排序对于GPU计算性能的影响
GPU的SIMT(Single Instruction Multiple Threads)能够使多个线程同时访问GPU全局内存,提高了数据吞吐能力。GPU的计算部件SM访问片上内存的带宽通常高于CPU的访存带宽,因此,有必要研究网格重排序对GPU计算的影响。本节只讨论显式计算在GPU上的性能。
显式计算在单GPU上400万网格规模下8个热点kernel的运行时间如表 8所示。无因次化(未排序kernel计算时间为标准)的kernel运行时间比较如图 16所示。由图16可知,网格重排序使得主要热点kernel的运行时间缩短了35%~60%。
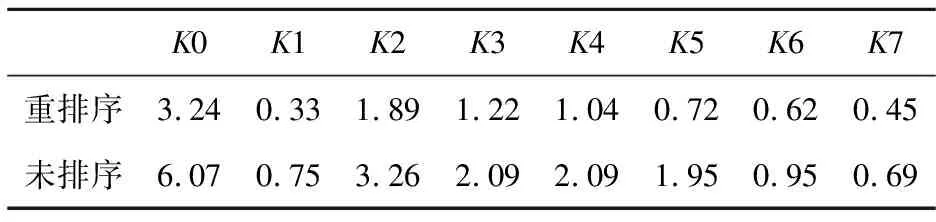
Table 8 Executing time of kernels for reordering and unordering

Figure 16 Comparison of hot spot kernels’ executing time before and after mesh reordering on GPU
网格重排序优化了数据在GPU全局内存中的分布,减少了数据间接访问带来的访存延迟,能够缩短大部分热点kernel的运行时间。
本文还记录了重排序前、后CFD程序在单GPU上的整体运行时间,如表 9所示。无因次化的运行时间如图 17所示。网格重排序使得显式求解CFD程序在GPU上的整体性能得到了提升,运行时间平均缩短了约40%。

Table 9 Comparison of explicit parallel computing’s executing time before and after grid reordering on GPU
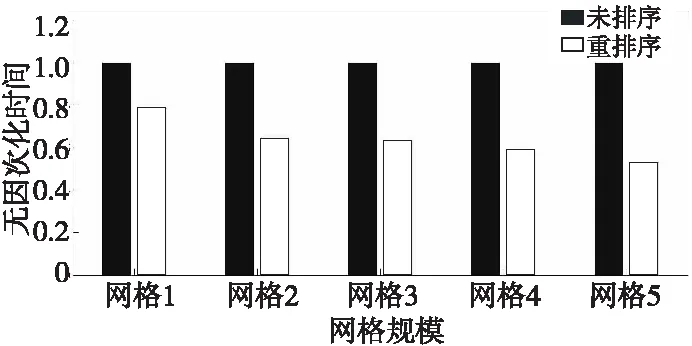
Figure 17 Comparison of explicit parallel computing’s executing time before and after mesh reordering on GPU
大部分热点kernel的运行时间缩短最终使得CFD程序的整体性能得到了提升。因此,网格编号重排序是一种全局性的优化策略。
网格重排序在GPU上的加速效果相比在CPU上的更加明显。这是GPU的访存模式造成的:GPU以32个线程组成1个warp,作为基本单位连续访问全局内存,直到访问完所需数据;GPU的L1 Cache只能保证空间局部性,不能保证时间局部性。因此,数据局部性的提高减少了GPU内存的访问频率,降低了访存延迟。对于CPU,数据局部性的优化只是提升了L1 Cache的空间局部性,对于时间局部性改善不大,访存延迟减少也有限。
5 结束语
本文采用网格重排序的方法优化了数据在内存中的分布。针对空气动力学中典型的三维机翼网格,分别在CPU和GPU上展开了多种规模的计算,发现网格重排序能提升数据局部性,减少访存延迟,提高计算效率。具体来说:
(1)网格重排序对计算精度的影响较小:排序前、后隐式计算的差异在0.5%以内,可以认为对显式计算的结果几乎没有影响。
(2)网格重排序能缩短计算时间。在CPU上,当体网格规模大于100万时,网格重排序能够缩短15%~20%的计算时间;在GPU上,主要计算热点在网格重排序后计算时间缩短了35%~60%,程序的整体运行时间也相应缩短了40%左右。
(3)网格重排序对GPU显式计算的优化效果更明显。
经过重排序后,部分函数的性能下降,这表明排序算法和具体函数的数据使用密切相关。未来会结合具体函数的数据使用特点开发、评估更多的排序算法。
致谢:感谢风雷软件团队和国家超级计算广州中心。

