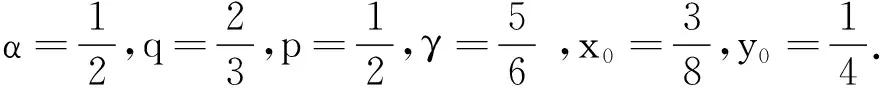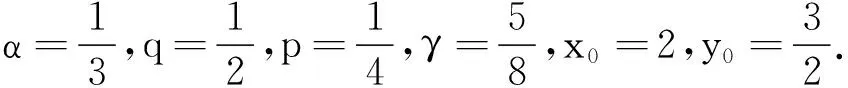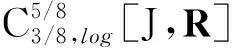一类分数阶微分方程边值问题解的存在唯一性*
黎逸云,谢景力
(吉首大学数学与统计学院,湖南 吉首 416000)
1 问题的提出
分数阶微积分因非常适合用来刻画具有记忆和遗传性质材料的过程,成为描述各类复杂力学与物理行为的数学模型[1-10].最近,不少学者在研究分数阶微分方程时取得了许多有趣的成果[4-10].例如,张海燕等[6]研究了一类Hadamard分数阶微分方程边值问题解的存在唯一性;Tariboon等[7]研究了一类Caputo和Hadamard型分数阶微分方程边值问题解的存在唯一性.受这些文献的启发,笔者拟研究如下一类Caputo和Hilfer-Hadamard型分数阶微分方程非局部边值问题解的存在唯一性:
(1)
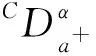
2 预备知识
设C[J,R]是包含了从J到R上所有的连续函数的Banach空间,空间上函数x的范数定义为
‖x‖C=max{|x(t)|:t∈[a,b]}.
连续函数x在区间[a,b]上的加权空间定义为
其范数为
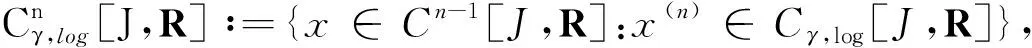
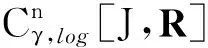
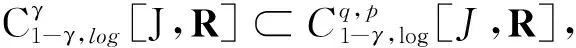
定义1[1]定义函数x:[a,+∞)→R的q阶Riemann-Liouville型分数阶积分为
其中Γ(·)是伽玛函数.
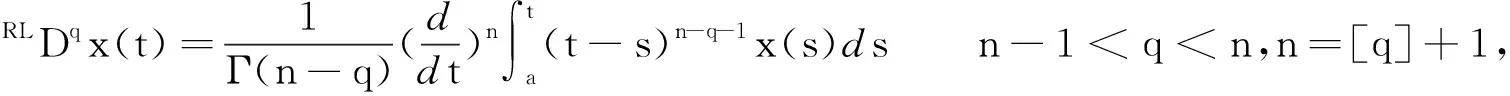
其中[q]表示实数q的整数部分.
定义3[1]对于至少n次可微函数x:[a,+∞)→R,定义q阶Caputo型分数阶导数为
引理1[1]令q>0,x∈C[J,R],则分数阶微分方程CDqx(t)=0的通解为
x(t)=c0+c1(t-a)+…+cn-1(t-a)n-1,
其中ci∈R,i=0,1,2,…,n-1(n=[q]+1).
引理2[1]假设x∈C[J,R],则对于∀q>0阶分数阶微分,有
RLIq(CDqx)(t)=x(t)+c0+c1(t-a)+…+cn-1(t-a)n-1,
其中ci∈R,i=0,1,2,…,n-1(n=[q]+1).
定义4[1]定义函数x:[a,+∞)→R的q阶Hadamard型分数阶积分为
其中log(·)=loge(·).
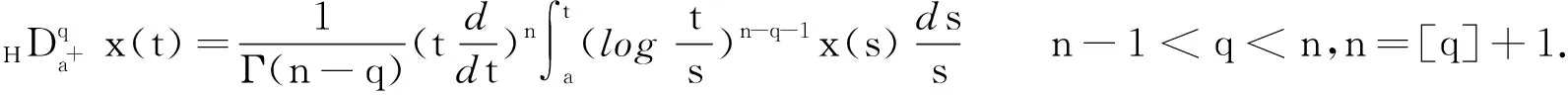

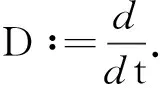
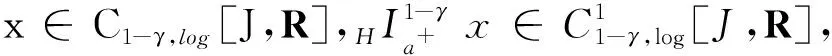
引理4[1]假设q,p>0,0 引理5[2](Banach压缩映射原理) 设E是Banach空间,D⊂E是闭集,T:D→D是一个压缩映射,即对于∀x,y∈D,有‖Tx-Ty‖≤k‖x-y‖(0 引理6[3](Krasnoselskii's不动点定理) 设D是Banach空间X中的一个非空有界凸子集.如果映射P,Q:D→X满足: (ⅰ)对于∀x,y∈D,都有Px+Qy∈D; (ⅱ)P是全连续的; (ⅲ)Q是压缩映射. 那么存在z∈D,使得z=Pz+Qz. (2) 的解,当且仅当x(t)满足分数阶积分方程 (3) 证明由引理2和引理3可知,问题(2)的等价积分方程为 (4) 由引理3和引理4(ⅰ)可得, 将c0,c1代入(4)式,即得(3)式.证毕. 定义算子T:C1-γ,log[J,R]→C1-γ,log[J,R]为 假设下列条件成立: (H1)存在函数φ∈C1-γ,log[J,R],使得对于∀t∈J,x1,x2∈C1-γ,log[J,R],有 |f(t,x1)-f(t,x2)|≤φ(t)‖x1-x2‖C1-γ,log. (H2)存在函数ψ∈C1-γ,log[J,R],使得对于∀t∈J,x∈C1-γ,log[J,R],有 |f(t,x)|≤ψ(t)(1+‖x‖C1-γ,log). 为了叙述方便,令 证明定义φ*=sup{|φ(t)|:t∈J},并设x1,x2∈C1-γ,log[J,R].对于∀t∈J,有 对于0<α<1,有(s-a)α≤(b-a)α,于是 定理3假设条件(H1)和(H2)成立,则问题(1)至少存在1个解. 首先,定义Br上的算子P,Q为 其次,将证明分为以下几个步骤: (ⅰ)证明(Px1+Qx2)(t)∈Br.当t∈J时,对于∀x1,x2∈Br,有 Mψ(1+r)+ω≤r, (ⅱ)证明算子Q在Br内为压缩映射.当t∈J时,对于∀x1,x2∈Br,有 (ⅲ)证明算子P在Br上是连续的.设xn,x∈C1-γ,log[J,R],n=1,2,…,且‖xn→x‖C1-γ,log→0(n→+∞).即对于∀t∈J,有xn(t)→x(t)(n→+∞).由于f是连续函数,因此 |f(s,xn(t))-f(s,x(t))|→0n→+∞. 根据Lebesgue控制收敛定理可知‖Pxn-Px‖C1-γ,log→0(n→+∞),故P在Br上连续. (ⅳ)证明算子P在Br上是紧的.先证明算子P在Br上一致有界.当t∈J时,对于∀x∈Br,有 Lψ(1+r)+ω≤r, 即PBr⊂Br,故算子P在Br上一致有界. 再证明算子P在Br上等度连续.对于∀x∈Br,a≤t1 当t1→t2时,有 因此P在Br上等度连续. 例1证明下列Caputo和Hilfer-Hadamard型分数阶微分方程非局部边值问题存在唯一解: (5) 例2证明下列Caputo和Hilfer-Hadamard型分数阶微分方程非局部边值问题存在解: (6)3 主要结果及其证明
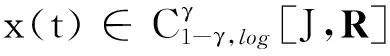
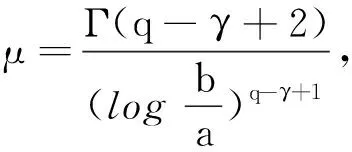
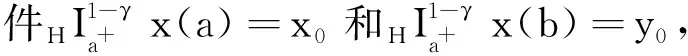
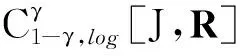

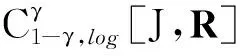

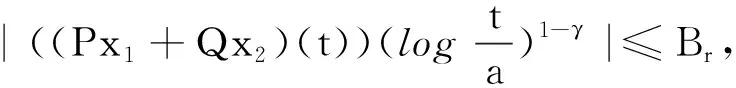
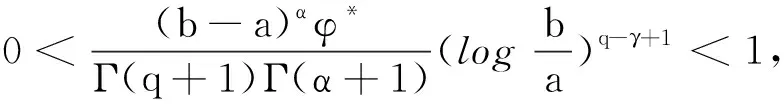
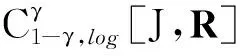
4 应用举例