非线性耦合长短波方程的格子Boltzmann模型求解*

宋通政，戴厚平，冯舒婷，魏雪丹

(吉首大学数学与统计学院，湖南 吉首 416000)

非线性耦合的长短波方程是物理学中一类重要的共振方程.1997 年，Djordjevic等[1]研究在二维毛细管-重力波运动时，首次提出了长短波方程，揭示了长波与短波之间存在共振相互作用.长短波方程因其丰富的物理和数学性质，被广泛应用于流体力学、等离子物理和化学物理等.近年来，学者采用各种数值方法如谱方法[2-3]、有限差分法[4-5]等求解长短波方程.这些方法的差分格式的计算较为复杂，不利于计算机编程，处理复杂的边界问题比较困难.

格子Boltzmann模型 (Lattice Boltzmann Model，LBM) 是一种新兴的数值方法.与传统的数值方法相比，LBM通过微观机制来研究宏观方程，它在宏观上是离散的，在微观上是连续的，具有物理背景清晰、边界条件易处理、并行性良好及程序易实施等特点[6-8].LBM已广泛应用于求解一些特殊的偏微分方程，如对流扩散方程[9]、KDV方程[10]和波动方程[11]等.鉴于LBM的独特优势，笔者拟尝试利用LBM求解一类非线性耦合的长短波方程的初边值问题.

1 长短波方程的格子Boltzmann模型

1.1 格子Boltzmann模型

考虑Benney在研究色散介质能量的非线性交换时提出的长短波方程[12]，其具体数学表达形式为

(1)

其中:η,β,α和λ为常数;复函数u(x,t)为短波的包络;实函数v(x,t)为长波的振幅;F(x,t)和G(x,t)分别为已知的复函数和实函数.短波u(x,t)通常用非线性Schrödinger型方程来解释,长波v(x,t)一般由带有色散的某类波函数来描述.

对方程(1)构建具有双分布函数的D1Q3格子Boltzmann模型.选用离散速度方向[c0,c1,c2]=[0,c,-c]，其中c为格子速度.采用如下形式的演化方程:

(2)

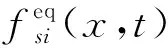
为了恢复宏观方程(1)，将(2)式等号左边对空间x和时间t进行Taylor展开，得到

(3)

再进行如下形式的Chapman-Enskog多尺度展开:

(4)

将方程组(4)代入(3)式，可得

(5)

比较(5)式两边ε同阶项的系数，可得O(ε0)的系数为

O(ε1)的系数为

(6)

O(ε2)的系数为

(7)

由(6) 式可得

(8)

将(8)式代入(7)式，可得

(9)

对(6)式两边关于i求和，得到

(10)

对(9)式两边关于i求和，得到

(11)

1.2 恢复短波方程

当s=1时，为了恢复短波方程，选择满足

(12)

(13)

将(12)式代入(10)式，可得

(14)

将(12)和(13)式代入(11)式，可得

(15)

将(15)式乘以ε后与(14)式相加，得到

1.3 恢复长波方程

当s=2时，为了恢复长波方程，选择满足

(16)

(17)

将(16)式代入(10)式，可得

(18)

将(16)和(17)式代入(11)式，可得

(19)

由(16)式可得

(20)

和

(21)

(22)

将(22)式代入(18)式，可得

(23)

将(23)式乘以ε后与(18)式相加，可恢复出如下长波方程:

2 数值算例

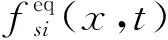
δAE(u)=|u(xk,t)-u*(xk,t)|,

其中u(xk,t)，u*(xk,t)分别为(xk,t)处的数值解和解析解.

例1考虑长短波方程组(1)中参数η=1，β=0.1，α=1，λ=1，函数

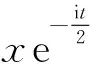
的情形.此时方程(1)的初边值问题有如下平面波解：

在数值实验中，计算区间为[0,π].图1给出了空间网格数N=100，Δt=0.000 1，T=2时|u|和v的精确解与新LBM解.由图1可见，新LBM解与精确解吻合得较好，具有很好的一致性.

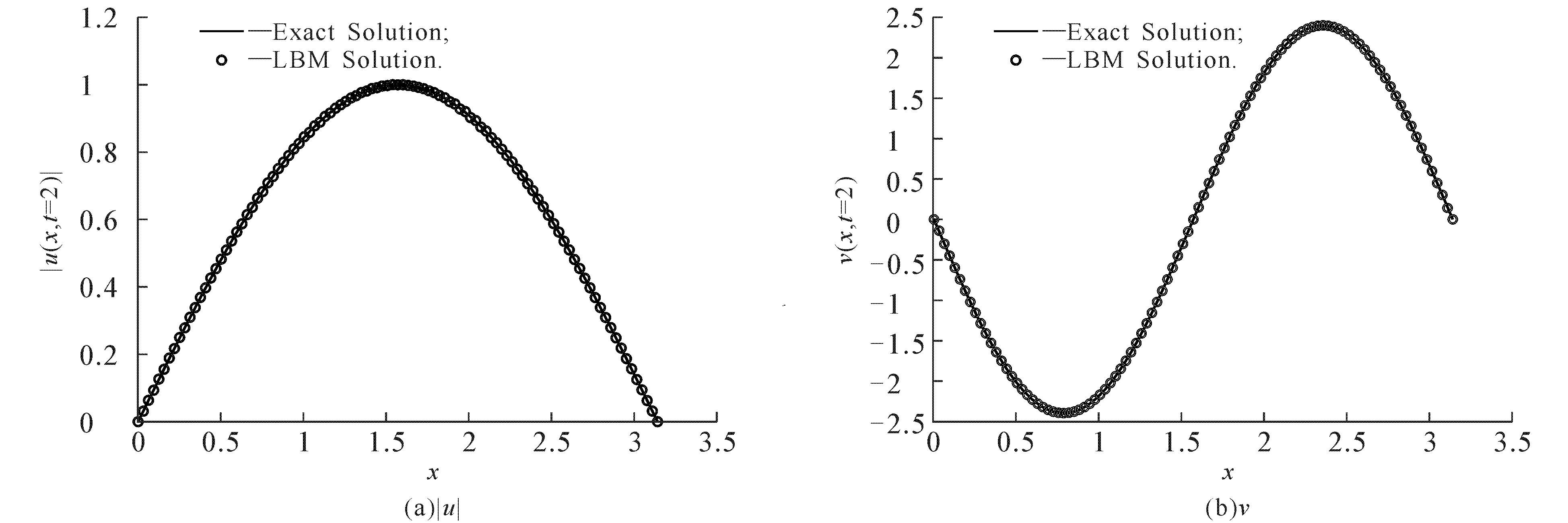
图1 T=2时|u|和v的精确解与新LBM解Fig. 1 Exact Solution and New LBM Solution of |u| and v with T=2

表1和表2分别表示空间网格数N=100，Δt=0.000 1，T=2时，u和v在不同位置节点的精确解与新LBM解.表1和表2可以进一步说明新LBM用于求解长短波方程的有效性.

表1 T=2时u在不同位置节点的精确解与新LBM解

表2 T=2时v在不同位置节点的精确解与新LBM解

表3给出了Δt=0.000 1，T=2时，不同空间网格数下u和v的误差分析.由表3可知，随着空间网格数的增大，u和v的全局相对误差都逐渐减小，且收敛阶均在2阶左右.这说明了新LBM是稳定且收敛的.

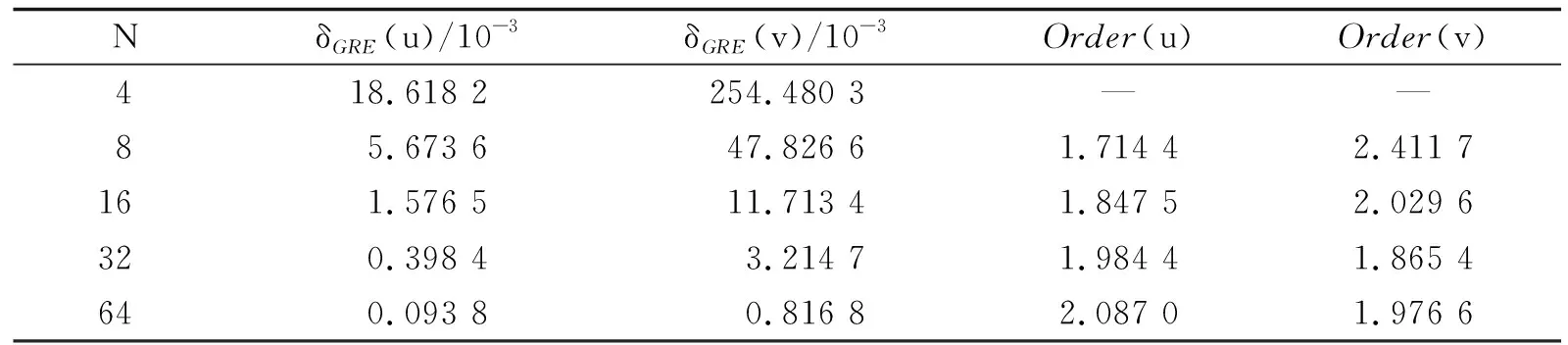
表3 T=2时不同空间网格数下u的误差分析

图2给出了空间网格数N=100，Δt=0.000 1，T=1时u和v的绝对误差.由图2可见，u和v的绝对误差均达到10-4数量级.

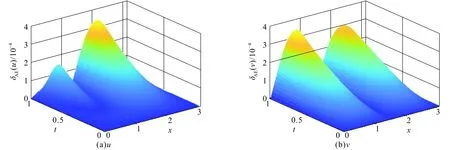
图2 T=1时u和v的绝对误差Fig. 2 Absolute Error of u and v with T=1

例2考虑方程组(1)中参数η=1，β=1，α=-1.5，λ=1，函数

的情形.此时方程(1)的初边值问题有如下孤立波解:

图3给出了空间网格数N=700，Δt=0.000 1，T=1时|u|和v的精确解与新LBM解.从图3可以看出，新LBM解与精确解十分吻合，具有很好的一致性.

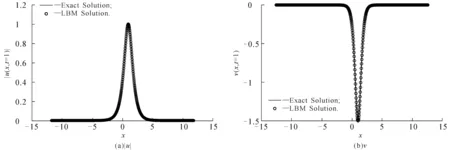
图3 T=1时 |u|和v的精确解与新LBM解Fig. 3 Exact Solution and New LBM Solution of |u| and v with T=1

表4给出了空间网格数N=700，Δt=0.000 1时，不同时刻T下u和v的全局相对误差.由表4可知，u和v的全局相对误差均在10-4数量级左右.

表4 不同时刻T下u和v的全局相对误差

图4给出了空间网格数N=700，Δt=0.000 1，T=0.5时u和v的绝对误差.由图4可见，u和v的绝对误差都达到10-4数量级.

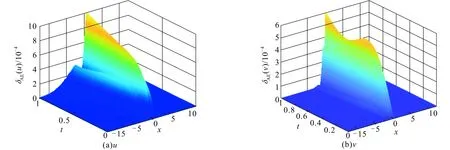
图4 T=0.5时u和v的绝对误差Fig. 4 Absolute Errors of u and v with T=0.5

3 结语

针对一类非线性耦合的长短波方程的初边值问题，利用引入平衡态分布函数和修正函数的D1Q3格子Boltzmann模型进行了求解.由数值算例可以看出数值解与精确解比较吻合，说明该模型可有效地求解这类非线性耦合的长短波方程的初边值问题.接下来，笔者考虑将本研究结果推广到更高维空间及分数阶长短波方程的初边值问题，进而拓展LBM在求解偏微分方程方向上的应用.