（3+1）维Boiti-Leon-Manna-Pempinelli方程的新精确解

林庆庆，黄发进，张明俊*，刘廷青，崔静易

（1.广西科技大学 理学院，广西 柳州 545006；2.柳州高级中学，广西 柳州 545006；3.中国地质大学（武汉）数学与物理学院，湖北 武汉 430074）

0 引言

近几十年来，非线性偏微分方程的精确解及其求法在研究非线性科学中具有重要意义，逐渐形成了考虑非线性自然现象的前沿和热点，受到了国内外各领域学者的高度关注。在许多自然科学领域，如物理学、流体力学、生物科学等，很多非线性现象可以用一些高阶非线性微分方程的数学模型来描述。因此，高阶非线性偏微分方程的精确解求法成为了数学领域中的研究热点，也是目前国内外数学和物理专家研究的主要对象，并具有非常大的挑战性。

1 预备知识

借助简单的线性常微分方程（式（2））来求解新的（3+1）维BLMP方程的变系数的新精确解。

2 古典（3+1）维BLMP 方程的新精确解

古典（3+1）维BLMP方程为：

令=+++，方程（3）转化为：

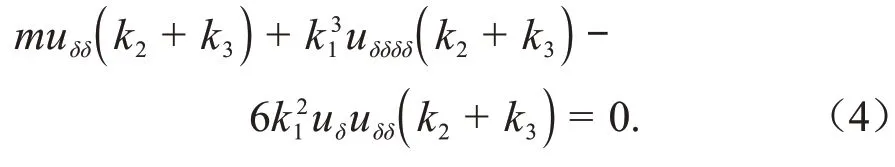
进一步，方程（4）两边关于积分可得：

其中、、、由后面的计算过程确定。

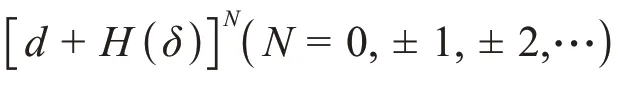
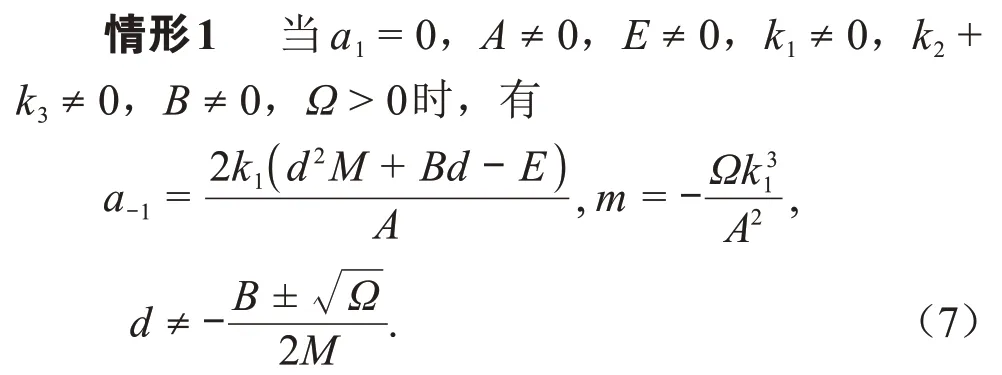
于是可得如下新精确解的表达形式：

其中=+++，=-，=+4，为任意常数，为任意非零常数。当参数满足式（7）的条件和关系时，上述的这些解就是所得到的具体的新精确解形式。

当=0时，有关系式如下：

所得到解的形式为：

当=0，≠0，≠0，≠0，+≠0，≠0，＜0时，

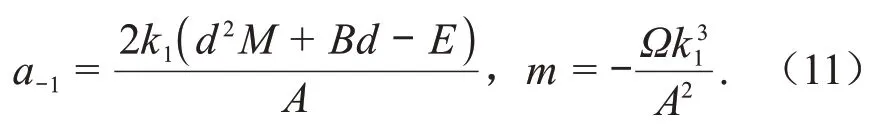
此种情况下，将上面的参数的关系式代入式（6）中，可得如下新精确解的表达形式：

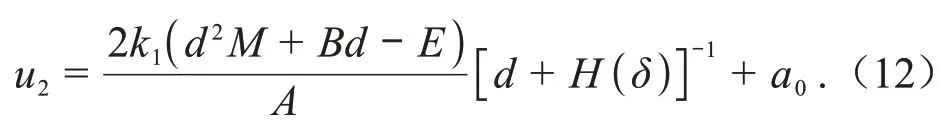
其中=+++，=-，=+4，、为任意常数，为任意非零常数。当参数满足式（11）的条件和关系时，上述的这些解就是所得到的新精确解形式。

当=0，≠0，≠0，≠0，+≠0，=0，＞0时，

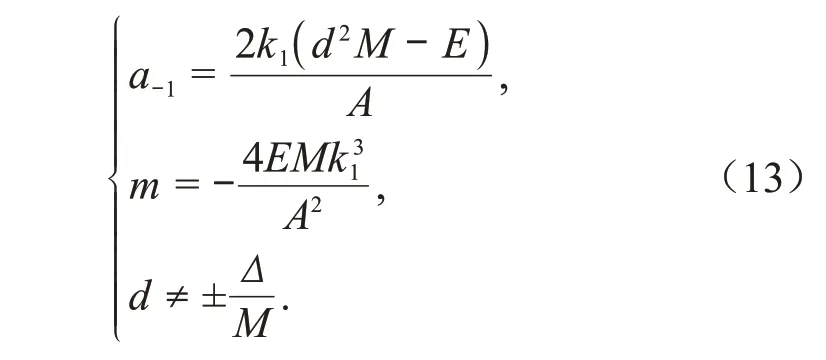
此种情况下，将上面的参数的关系式代入式（14）中，可得如下新精确解的表达形式：

其中=+++，=-，=，为任意常数，为任意非零常数。当参数满足式（13）的条件和关系时，上述的这些解就是所得到的具体新精确解形式。

当=0，≠0，≠0，≠0，+≠0，=0，＜0时，

此种情况下，可得如下新精确解的表达形式：

当参数满足式（16）的条件和关系时，上述的这些解就是所得到的具体的新精确解形式。

当=0，≠0，≠0，≠0，+≠0，≠0，≠0时，

此种情况下，可得如下新精确解的表达形式：

当参数满足式（17）的条件和关系时，上述的这些解就是所得到的具体的新精确解形式。

对上述的不同情形下的解，给出相应的解的图形。

利用MAPLE 软件可以得到的图形，如图1所示。

图1 当B ≠0，Ω ＞0时，u1的图形

利用MAPLE 软件可以得到的图形，如图2所示。

图2 当B ≠0，Ω ＜0时，u2的图形

利用MAPLE 软件可以得到的图形，如图3所示。

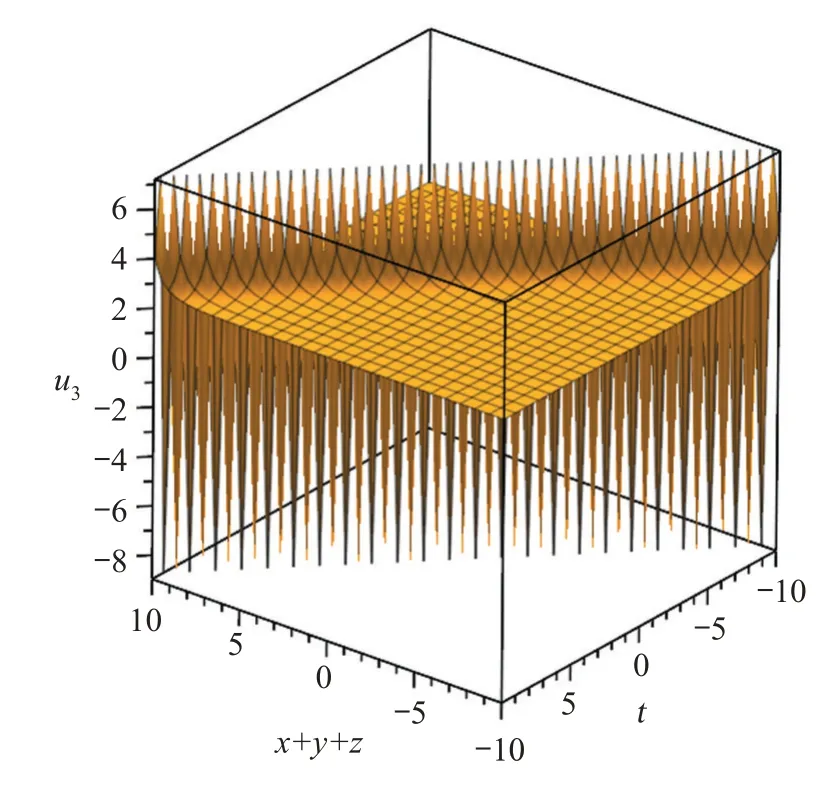
图3 当B=0，Δ ＞0时，u3的图形

利用MAPLE 软件可以得到的图形，如图4所示。

图4 当B=0，Δ ＜0时，u4的图形

利用MAPLE 软件可以得到的图形，如图5所示。

图5 当B ≠0，Ω ≠0时，u5的图形

3 新的（3+1）维BLMP方程变系数的精确解

通过对旧的（3+1）维-BLMP 方程进行修正，得到新的（3+1）维BLMP方程：

设方程（19）有如下变系数形式的解：

其中a是关于、、、的函数。=()满足如下的二阶常微分方程：

解方程（21）有3种形式的解：

将方程（21）的解代入-，类似于文献[6]，最后会得到多种不同的形式解。

下面给出这些解的图形。以为例，在-4＞0、-4＜0、-4=0这3种情况下讨论解的不同结构。

1）当-4＞0时，取=3，=2，===(-)+(-)+，()=，===1，=2，=0，=1，=2。此时

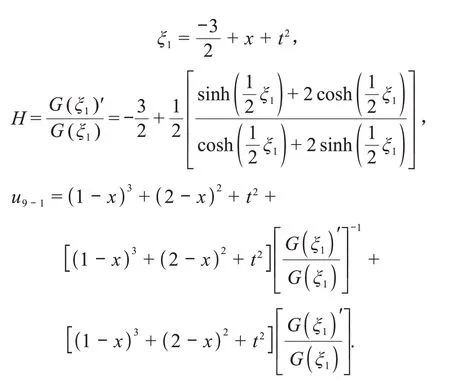
利用MAPLE 软件得到的图形，如图6所示。

图6 λ2 -4μ ＞0时，u9-1的图形

2）当-4＜0 时，取=1，=2.5，===(-)+(-)+，()=，===1，=2，=0，=1，=2。此时

利用MAPLE软件得到的图形，如图7所示。

图7 λ2 -4μ ＜0时，u9-2的图形

3）当-4=0时，取=4，=4，===(-)+(-)+，()=，===1，=2，=0，=1，=2，此时

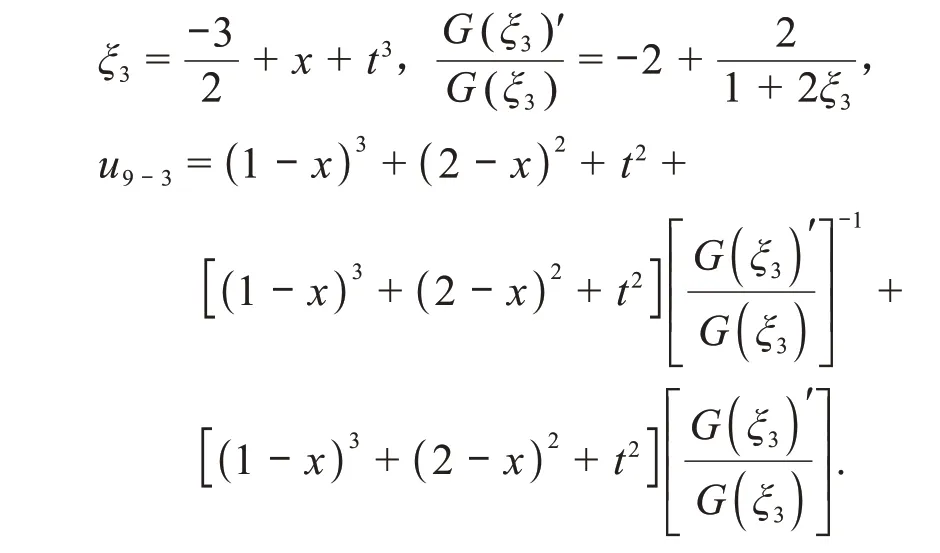
利用MAPLE软件得到的图形，如图8所示。

图8 λ2 -4μ=0时，u9-3的图形

4 总结

本文对古典的和新的（3+1）维BLMP方程分别从常系数和变系数的测试函数出发，得到了相应的新的精确解的形式。特别是对于新的BLMP方程来讲是一种变系数的精确解形式，目前研究较少。这种思想可以推广到求解其他的非线性偏微分方程的变系数精确解形式。这些精确解在进一步解释自然界中的非线性现象方面具有一定的数学理论依据。