液体晃动动态性能实验设计与数据后处理方法研究

姜丙超，吴文军，王 佐，高超南

（广西科技大学 机械与汽车工程学院，广西 柳州 545616）

0 引言

液罐车在行驶时，车身晃动、速度变化、紧急制动和快速转向等情况均会引发液罐车罐体内液体晃动，使液罐车的行驶稳定性降低，严重时甚至造成侧翻。液罐车所装载液体多为化学危险品，侧翻时易引发泄露、爆炸等危害，对人身安全、当地交通和事故发生地的自然环境造成威胁，因此，研究罐车内的液体晃动有着重要的意义。

研究液体晃动的主流方法有理论解析法、数值仿真法以及实验研究法。其中，实验研究法不仅能获取大量真实可靠的液体晃动数据，还能直观地看到液体晃动现象，更方便揭示液体晃动的本质特征；而数值仿真法基于计算流体力学（computational fluid dynamics，CFD）理论，借助计算机制成计算流体力学商业软件，科学有效地求解各种流体流动问题，具有计算快、操作简便、不受场地限制等优点。

在实验平台设计思路上：曾世荣对实验平台施加垂直激励来模拟垂直地震激励；张海涛等施加横向简谐外部激励；Kotrasová等对实验平台施加单向和三向简谐波；Akyildiz 等在论文中提到一款实验平台，利用直流电机实现了平台的俯仰运动；卫志军等提出了一种六自由度平台，并分析了实验误差，验证了平台的准确性；Wu 等利用六自由度实验平台模拟了船舶在海水中遇到极端天气时，罐内液体晃动时自由液面的变化，获得了晃动冲击载荷特性。

在监测液体晃动方面：Lobovsky等使用摄像机记录液体表面轮廓的演变，并使用压力传感器测量壁上液体的压力；Antuono 等使用压电式力传感器测量油箱的表面力和力矩；Carra 等使用激光多普勒测振仪实现了壁面响应的非接触测量，为监测液面提供了新思路；Gándara 等使用超声波传感器跟踪自由表面的演变，并使用高速摄像机记录实验。

Martinez-Carrascal 等提出了2 种晃动力计算方法，用于探索飞机加速时油箱中液体的晃动力，提高晃动力测量的精度。胡齐等通过自由衰减实验获得晃动频率、晃动质心高度、晃动阻尼比，通过强迫晃动实验获得贮箱晃动质量、总质量等参数。刘奎等用ⅤOF 法模拟了液罐车转向时液体的晃动，记录了储罐壁受到的作用力的峰值随向心加速度的变化。

由上述文献可知，前人在平台设计、液面检测、数据处理等方面提供了很多设计思路，但是对导致液罐车侧翻或倾覆的直接原因——液体对贮箱壁的作用力和作用力矩的研究较少。本文结合前人的经验和不足，设计了一种可以准确测量晃动力和晃动力矩的液体晃动实验平台。

1 实验装置和实验原理

所设计的平台装置应以高效且准确地采集晃动力和晃动力矩为主要目的，为此，应用3个单轴力和1个三轴力传感器设计出一种实验平台，该平台既能实现充液贮箱结构的固定安装，又能实现最大化地测量贮箱内液体晃动产生的非平衡晃动力和晃动力矩。传感器分布、实验平台结构分别如图1、图2所示。

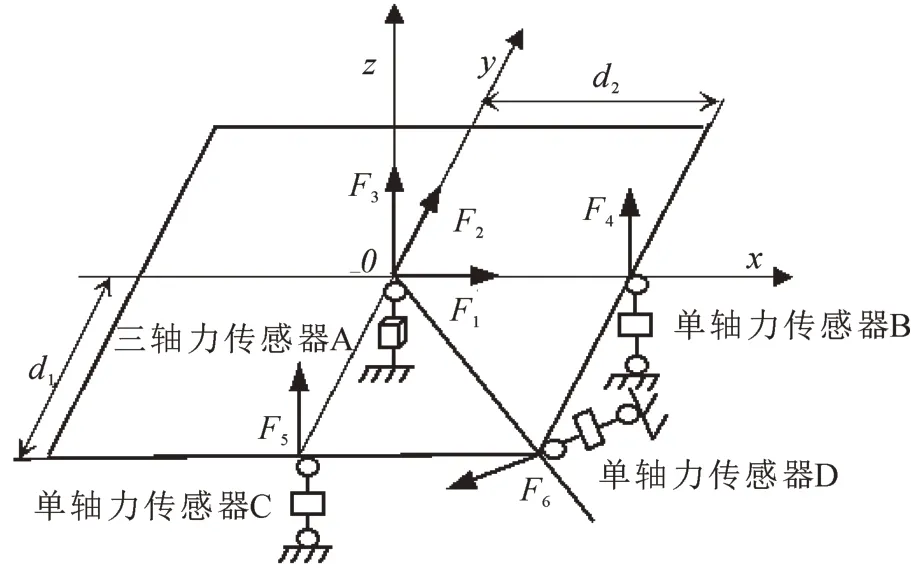
图1 传感器分布及原理图

图2 实验平台结构示意图

如图1所示，以三轴传感器A与支撑板的交点为坐标轴原点，建立三维坐标，激振器激励方向为轴。其中，三轴传感器A沿轴所采集的力、、分别为贮箱内液体对贮箱在方向上的作用力，、分别是单轴力传感器B、C所采集的晃动力矩数据，是单轴力传感器D所采集的绕轴的晃动力矩。

如图2 所示，实验平台主要由滑块滑轨组合、支撑板、Cassini 贮箱、Cassini 贮箱底座、力传感器、加速度传感器、正反牙球铰、正反牙螺母和地脚螺栓等零部件组成。其中地脚螺栓可以调节晃动平台的水平度，是保证实验正常进行的基础，也是后期调平的方式之一。滑块滑轨之间点接触式的滑动摩擦极大降低了摩擦力，提升了实验精确度。贮箱底座可有效固定Cassini贮箱，且安装简便快捷。晃动平台的贮箱支撑板对标多种类型贮箱设计，可配合不同种类的贮箱底座，满足球形、圆柱形、Cassini形等贮箱的测量。

为了最大化地满足汽车运输过程中可能遇到的激发频率，方便后期研究贮箱内的液体有限幅稳态晃动的行为特征和动力学特性，选用可以产生频率范围为0.01～400 Hz 简谐信号的DG5102 信号发生器。为适配激振器且方便调节信号幅值，采用功率放大器处理该简谐信号。激振器接收放大后的信号带动晃动平台，激励贮箱内液体产生不同类型的晃动行为。整个液体晃动动力学实验平台装置主要由信号发生器、功率放大器、激振器、动态信号采集仪及自主设计的贮箱夹紧装置等仪器设备构成，所需设备的型号和数量如表1所示。

表1 设备型号及数量表

液罐车贮箱可近似看成横置的Cassini 贮箱，结合现有条件和现有材料，用横置Cassini 贮箱代替液罐车贮箱。储罐设计参数：Cassini贮箱两端为半球，中间为圆柱形的容器，有效容积6 L，圆柱半径为100 mm，前后封头为标准半球形，半球球径为100 mm。贮箱总长为410 mm，贮箱壁厚均为5 mm，材料为亚克力。Cassini贮箱及尺寸图见图3。

图3 Cassini贮箱及尺寸图（单位：mm）

系统操作步骤如下：1）信号发生器产生低功率电信号；2）通过调节功率放大器，产生满足实验要求并与激振器相适应的电信号；3）激励器产生恒定振幅正弦波加速度，使整个实验平台震动；4）力信号由力传感器监测，加速度传感器测量加速度信号，并由信号采集仪收集，然后通过集成线路实时传输至计算机；5）力和加速度信息显示在计算机数据分析软件上。实验流程如图4所示。

图4 实验流程图

2 传感器准确性检测

2.1 加速度传感器准确性检测

在支撑板两侧分别固定2个不同的加速度传感器，在频率为2.0 Hz的简谐激励下测得2组加速度数据，如图5所示。

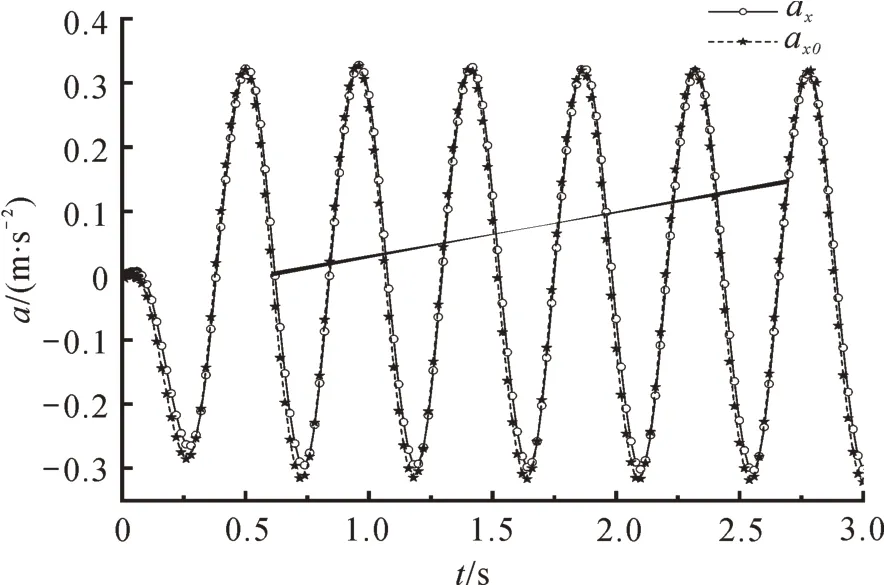
图5 加速度传感器数据对比

由图5可知，2组传感器数据波形吻合度良好，频率、振幅稳定，且波形最大值和最小值的绝对值均为0.325，说明加速度传感器性能稳定，实验过程晃动平稳，平台水平度良好。使用MATLAB 软件对所测加速度数据进行离散傅里叶变换，得到如图6所示的频域图。由频域图可知，加速度识别频率为2.003 Hz，与信号发生器输出频率相差仅0.003 Hz，误差为0.15%，说明2 个加速度传感器灵敏度强，精确度高。虽然由于导轨与滑块之间的摩擦、自身性能的限制等原因导致两波形有微小的差别，但可忽略不计。

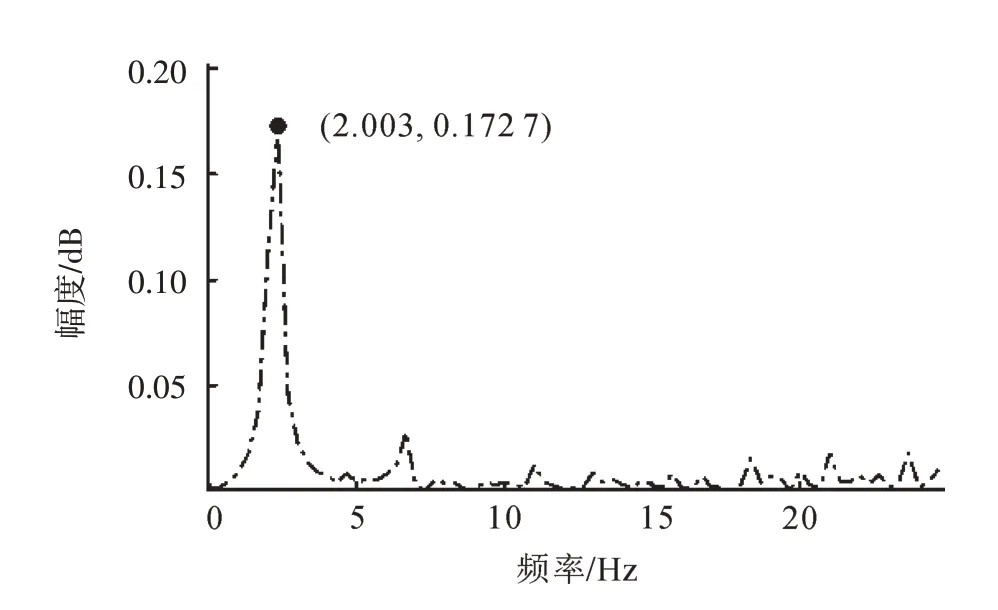
图6 频域图

2.2 力传感器准确性检测

2.2.1 灵敏度拟合

本实验对力传感器的灵敏度有很高的要求，为了得到准确的晃动力和晃动力矩，需要对力传感器进行动态验证。依据力传感器灵敏度工作原理，力传感器承受的轴力F与所采集电压信号u的关系曲线可以描述为：

式中：为传感器灵敏度；ε是测量误差，随时间变化的总误差近似为0。为降低测量误差对传感器灵敏度计算的影响，依据最小二乘法原理，总误差的平方为：

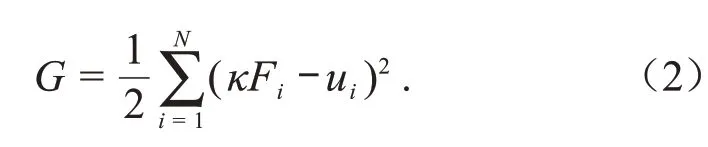
对式（2）求的偏导，并令偏导数为0，最终得到力传感器灵敏度的计算公式为：

实验中具体采集和计算过程为：1）设置力传感器的灵敏度为1 mv/Ⅴ；2）力传感器下方固定，上方安装称重托盘；3）依次向托盘中增加等重量的标准砝码，并采集电压值；4）利用式（1）初步求得灵敏度；5）利用最小二乘法和MATLAB软件进行曲线拟合，得到灵敏度值；6）重复上述步骤，分别得到所有力传感器的灵敏度。最终得到的实验数据和最小二乘法拟合图如图7所示。

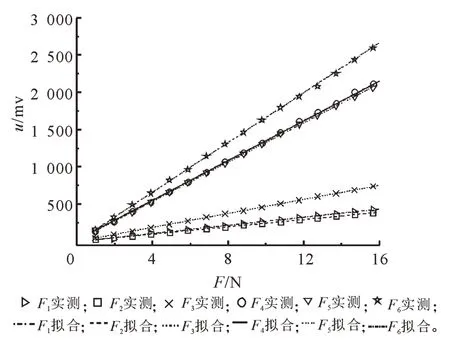
图7 最小二乘法拟合图

2.2.2 静态性能校核

将求得的灵敏度数值在采集系统上进行设置，采取与上文的灵敏度检测一样的实验步骤进行校核。对比采集的压力值与真实值发现，所有力传感器的测量误差均在1%以内，表明静态法所求的力传感器灵敏度数值精确。因篇幅有限，仅在表2中列出三轴力传感器方向的验证误差表。

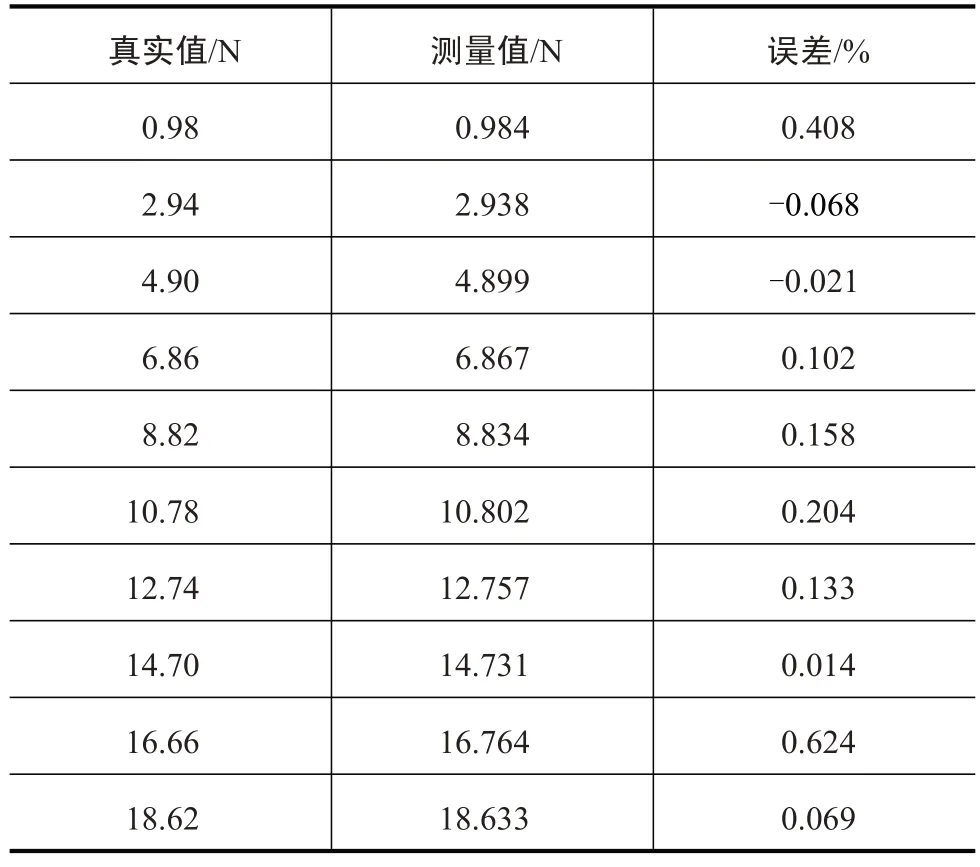
表2 力传感器静态验证误差表

2.2.3 动态性能校核

动态系统下灵敏度精确性验证是为了验证力传感器在不同频率激励下仍能保证测量结果的准确性。为此以一个质量为1.504 kg 的铝块进行质量识别实验。实验装置如图8 所示，力传感器、铝块和加速度传感器粘贴在激振器输出端。激励频率幅值不变，频率范围设为1.5～3.0 Hz，每组一个固定频率，每次新实验增加0.2 Hz。通过对激振器输入不同频率的正弦信号，利用测得的加速度和轴力值，进一步运用最小二乘法识别出铝块的质量，从而检验了力传感器在动态测量系统中的可靠性。

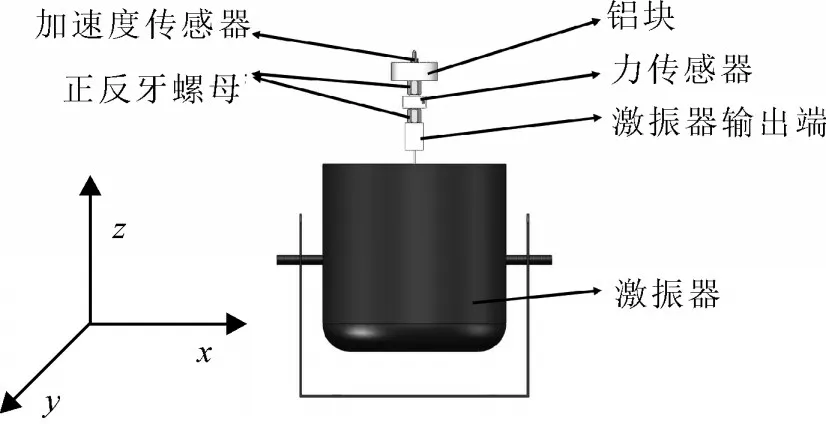
图8 质量识别实验示意图

实验可测得力F和加速度随时间的变化。已知铝块的实际质量，力传感器的测量误差为，为此需要求得三者之间的关系，并且平衡实验测量误差。由牛顿第二定律得到：

为降低测量误差的影响，由最小二乘法优化铝块质量的求解公式：

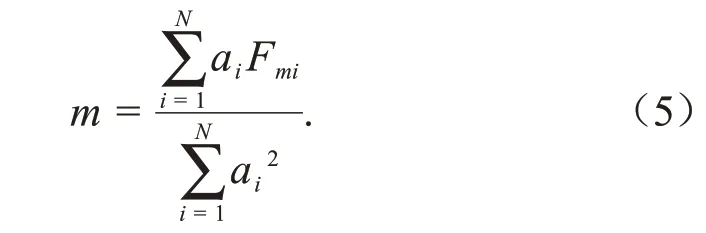
将测得的力和加速度随时间变化的数据代入MATLAB 软件中，得到系统在运动情况下力传感器测量出的铝块质量如表3 所示。从表中可以看出，实验测量的铝块质量与铝块的实际质量基本一致，识别误差均在1%以内，说明力传感器在动态系统中的精度很高，证明了其可靠性，为后续实验的精确测量提供了有力保证。

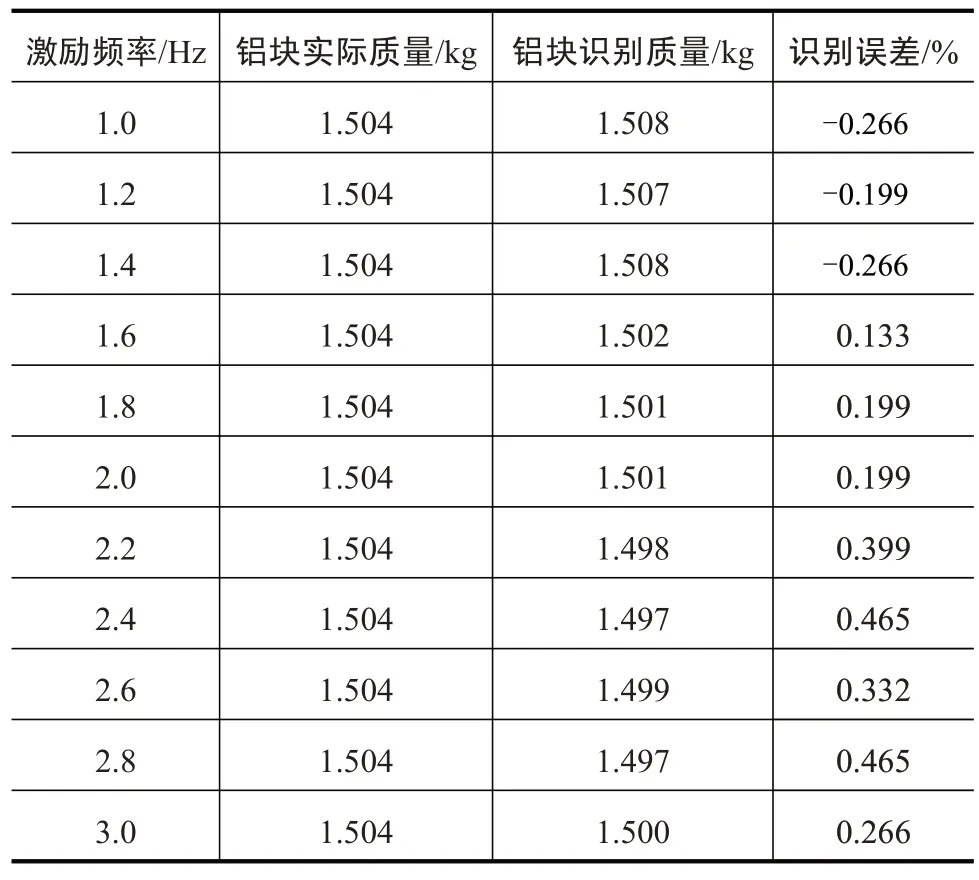
表3 动态测量系统可靠性检验的实验结果

3 晃动实验过程

实验过程的正确操作能极大提高实验的成功率。为了准确分析液体晃动动力学特性和揭示液体晃动固有特性，需尽量避免实验设备工作状态的不稳定和人为操作误差影响实验结果，因此实验过程严格按以下标准步骤进行：

1）实验设备预热

因为所用传感器精度较高，所以正式实验开始前，为了使机器更好地进入检测和测量状态，需打开所有设备，预热0.5 h。提前设置好激励幅值，安装好Cassini横置贮箱底座，固定Cassini贮箱。

2）测量通道设置

打开数据采集分析系统软件，在所有通道软件设置界面设置所接传感器类型、型号、输入方式、灵敏度、测量单位和编号；加速度传感器为压电式传感器，设置类型为IEPE 型。力传感器设置为差分直流输入，其中，三轴力传感器A 沿、、坐标方向所测的力信号对应1～3通道，单轴力传感器B、C、D 分别对应4～6通道，加速度传感器对应7通道。查询对应传感器灵敏度并进行设置，设置采样频率为50 Hz。

3）滤波器设置

为去除电路中不需要的信号，需选择合适的滤波器。因为液体晃动非线性明显，且所需要的激励频率范围较低，仅为1.0～4.0 Hz，所以选择IIR 滤波器，滤波方式为低通滤波。根据实验要求选择一组合适的通带平坦度和阻带衰减，使滤波器的效果达到最好并保证其稳定性。

4）平衡清零及采集过程说明

平衡清零有助于对零点位置进行校准，将上一组实验带来的电信号影响降到最低，在信号发生器选择好所需的输出信号频率和幅值。当以上所有参数设置结束后，选择平衡清零，将所有通道数据清零。每做一组实验都需要平衡清零。

点击采集按钮，设置好储存地址和名称。点击信号发生器输出按钮使其工作，激振器带动实验晃动平台运动，采集分析系统自动采集所需原始数据并可将原始数据保存成所需要的格式。

4 数据处理方法

支撑板、Cassini 贮箱底座和Cassini 贮箱通过螺栓等方式固定，可将其看成一个整体，称为固件，它们的重量称为固件质量。当固件在激振器强迫激励下移动时会产生惯性，导致测量的数据不仅有晃动力和晃动力矩，还包括惯性力和惯性力矩，因此，应除去惯性力和惯性力矩。力传感器和加速度传感器不可避免地会产生测量误差，为此引入力传感器的测量误差（）和加速度传感器测量误差（）2个随机变量。由于实验数据随时间连续变化，因此，在激发时间内，2个变量的平均值视为0。图9为实验所用平台固件质量和质心高度示意图。

图9 Cassini贮箱固件质量与质心距离示意图

由牛顿第二定律得：

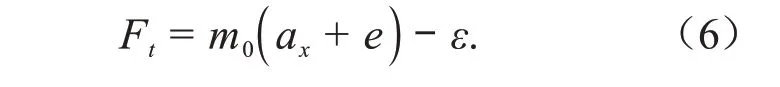
式中，a为固件加速度。总误差的平方为：

为求总误差平方的最小值，将式（7）求偏导，并令偏导数为0，最终求得固件总质量的无偏估计量：

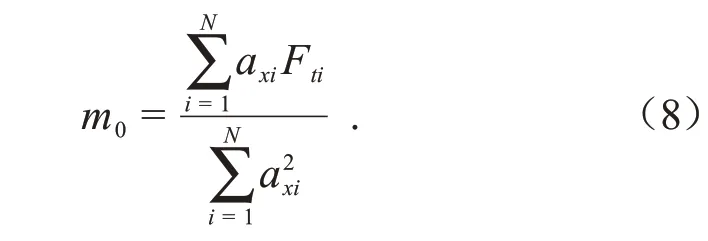
同理，由最小二乘法计算质心高度的无偏估计量：

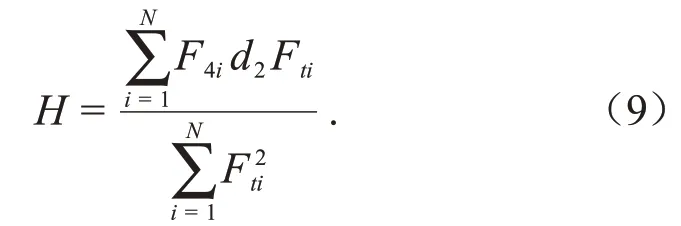
最终可得真实的液体晃动产生的动态晃动力和晃动力矩分别为：

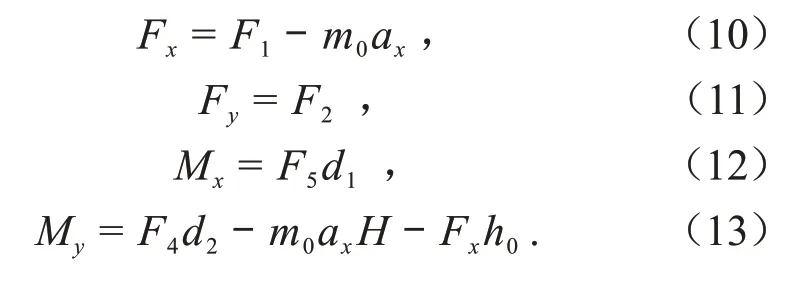
5 实验与仿真对比

为进一步验证实验台的合理性、可靠性，将2种研究方法互相结合，将实验所测和仿真得到的轴向晃动力、绕轴的晃动力矩进行对比。

5.1 定频率激励实验

以40%充液比为例，向贮箱内灌注4.189 kg的水。设定激励的峰值为3.0 vpp，给定激励频率分别为1.0 Hz、2.0 Hz 和3.0 Hz。为了保证CFD 仿真外激励与实验外激励一样，将实验所采集的加速度数据导入CFD 仿真软件中。为排除实验偶然性，每频率进行多组独立重复的实验。

5.2 仿真分析

1）在三维建模软件上构建贮箱模型并抽取罐体的流体域。

2）设置边界条件，壁面条件为无滑移。选择一种液体且不可压缩液体，设置液体种类为20 ℃时的水。初始时刻两相流按充液比分层分布，上层为空气，下层为水。

3）设定轴负方向加速度为9.8 m/s²，将实验所采集的沿轴方向加速度数据导入CFD软件中，设定加速度激励时间为60 s，设置黏度和震荡。

4）对模型进行网格划分，采用结构六面体网格。图10 是当模型划分网格数分别为50 000、70 000、90 000、100 000、120 000、140 000 时液体产生的最大晃动力。由图10 可知，当网格数在100 000 以上时对最大晃动力数值影响不大。结合计算机运算速率和前人对石油气储罐网格划分的经验，最后选择网格数为200 000 个。网格划分如图11（a）所示。

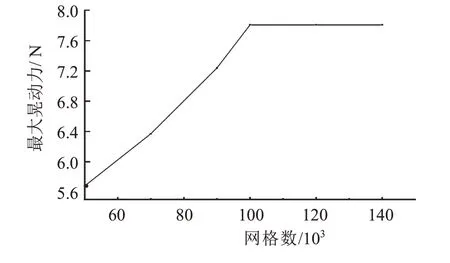
图10 最大晃动力随网格数的变化

5）对贮箱充入液体的方法有3种：给定液体高度法、给定体积法、给定波边界法。本文选用给定体积法，以方便后续研究液体晃动特性与充液比的关系。给定充液比为40%，如图11（b）所示。

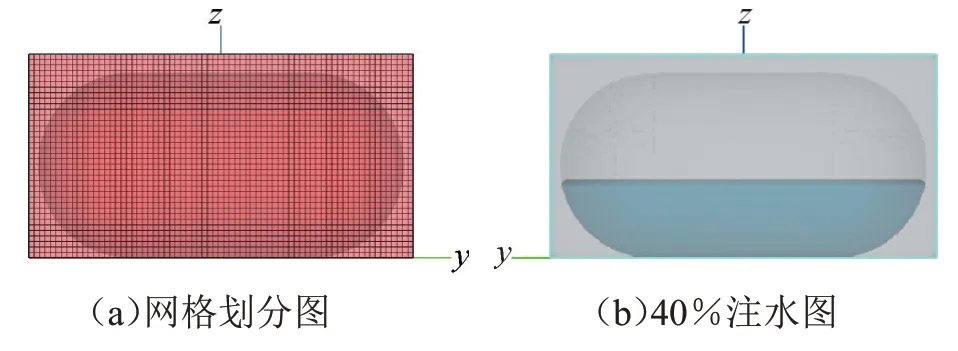
图11 Cassini贮箱网格划分和注水图

6）设置输出采样频率为50 Hz。设置依据为实验设置的采样频率为50 Hz，二者保持一致。

7）运算并得到结果。根据需要选择有用的数据，包括时间（每0.02 s进行一次采样），、轴方向晃动力和晃动力矩，三维运动仿真演示等。其中三维运动仿真演示可以帮助观察实验现象是否一致。而、轴方向的晃动力、晃动力矩可与实验采集数据进行对比。

5.3 实验与仿真数据对比

外激励为1.0 Hz时（见图12），贮箱内液体晃动行为是大振幅驻波运动，晃动剧烈，但晃动行为稳定。因此，在该激励频率下，轴向力和绕轴方向力矩很大，但晃动力和力矩最大值稳定。外激励为2.0 Hz时（见图13），液体晃动行为为一阶晃动和二阶晃动混合发生，晃动行为混乱，故力和力矩时域图相邻2个波峰之间有较多的杂波，且液体晃动引发的晃动力和力矩很小。外激励为3.0 Hz 时（见图14），液体晃动行为是高阶模态晃动，力和力矩也很小。由以上对比图发现，实验值与仿真值相位有误差，实验值比仿真值要晚一个微小时间。这是因为实验时激振器启动有一个极短的启动延迟，而仿真时没有；实验所测力和力矩比仿真值大，是因为导轨与滑块的摩擦力虽然很小，但仍然存在这样一个微小的摩擦力。虽然存在一些误差，但所测力和力矩周期、变化趋势等均吻合良好，有效验证了实验系统的合理性、实验平台调试的准确性。

图12 （网络版彩图）外激励1.0 Hz时的晃动力和晃动力矩

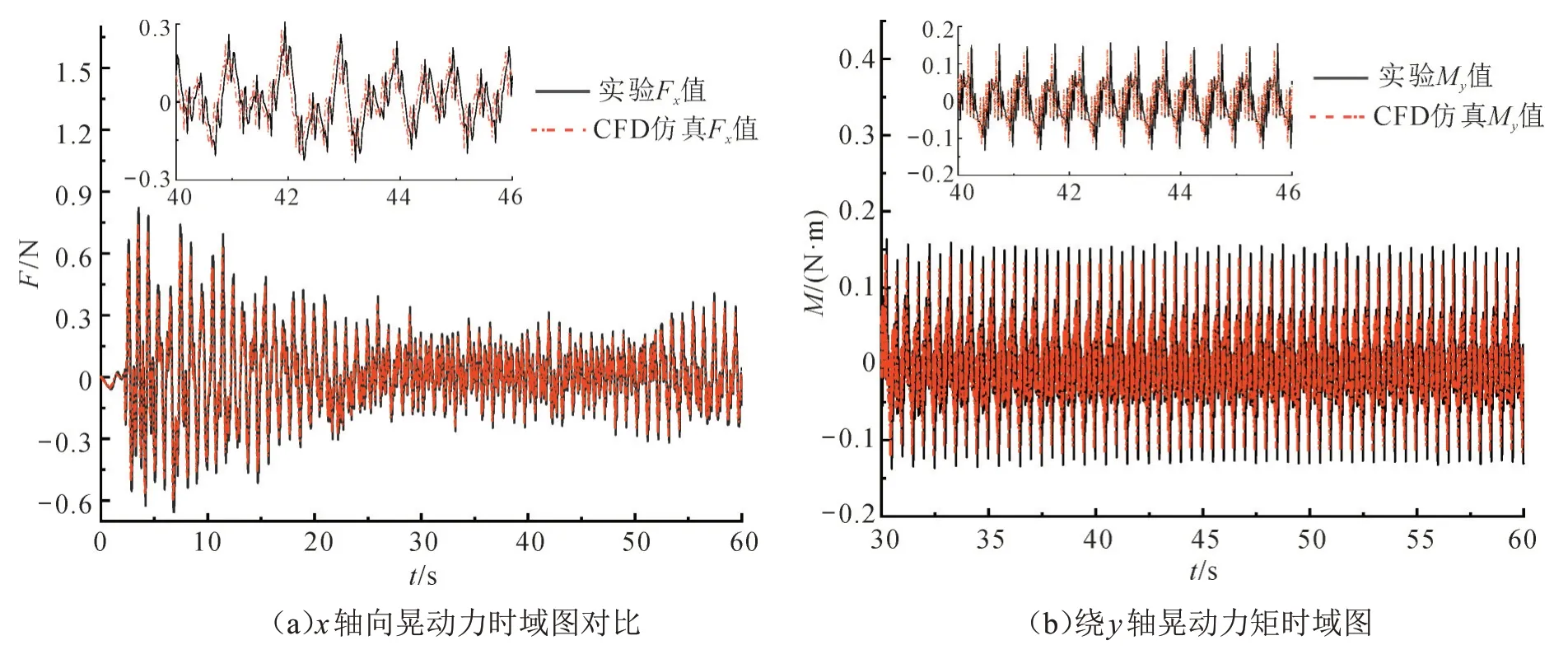
图13 （网络版彩图）外激励2.0 Hz时的晃动力和晃动力矩

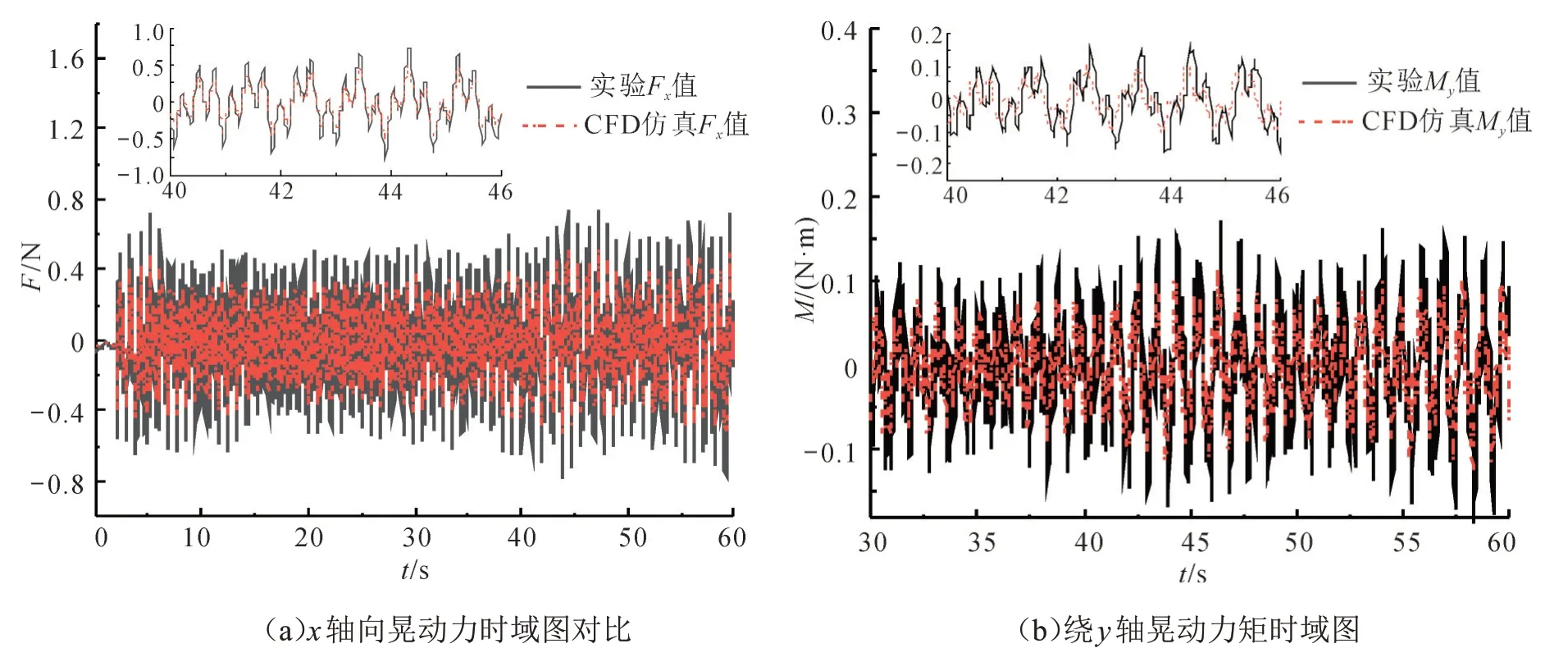
图14 （网络版彩图）外激励3.0 Hz时的晃动力和晃动力矩

6 结论

本文从传感器分布、实验平台结构和晃动实验流程3个方面介绍了一种在横向激励下测量贮箱内液体晃动力和力矩的实验装置，给出合理的数据处理方法，并验证了实验系统的准确性。

1）验证加速度传感器的准确性。在支撑板不同位置固定2个加速度传感器，使用2.0 Hz对比得到2组对比度良好的加速度数据，且所测数据经过傅里叶变换后得到的频率与实际激励频率误差仅0.15%，进一步验证了加速度传感器的准确性。

2）验证力传感器准确性。利用最小二乘法求得力传感器灵敏度的计算公式，设计静态、动态2种实验来验证力传感器的准确性，且2种实验的测量误差均小于1%。

3）给出合理的数据处理方法。利用最小二乘法对力传感器采集到的整体动态数据进行处理，去除了固件惯性和零均值测量误差的影响，得到了真实反映液体晃动规律的晃动力和晃动力矩。

4）实验与仿真对比验证实验平台的准确性。开展定频、定幅值激励实验，分别以1.0 Hz、2.0 Hz、3.0 Hz 的频率激励充液比为40%的Cassini 贮箱，结合CFD 仿真，对比处理后的实验数据与仿真数据，结果表明：力和力矩大小、震荡周期、晃动力和晃动力矩的幅值变化趋势等均吻合良好。

通过以上实验，有效验证了实验系统和数据处理的合理性以及实验平台调试的准确性，为将来研究液罐车贮箱内液体晃动和动力学特性打下一定的实验基础。