经管类专业“运筹学”渐进式教学方法

陆 彪

（南京航空航天大学 经济与管理学院，江苏 南京 211106）

引言

“运筹学”是经济管理类专业的重要基础课程之一。运筹学致力于解决经济管理领域的决策问题，通过采用定量方法，辅助管理者做出优化决策。运筹学涉及十几个分支，如线性规划、运输问题、动态规划、图论与网络计划、决策分析、存储论、排队论等。各分支都有一套独特的方法体系，各方法体系之间的关联性较弱。从该角度而言，“运筹学”是一个内涵非常丰富的课程。对于经管专业的学生而言，学好运筹学，掌握其思想和方法，可以为从事经济管理方面的工作或研究打下坚实基础。

由于“运筹学”包含的分支众多，而且各分支方法差异较大，因此学好运筹学并非易事。同时，各分支方法都要求建立和解析数学模型，而经管类学生数学功底较弱，这增加了他们学好该门课程的难度。因此，作为经管类专业运筹学授课教师，必须寻求有效的教学方法以引导学生学好该门课程。事实上，虽然运筹学中各分支方法差异较大，但它们都遵循同样的底层逻辑：首先根据实际问题构建数学模型，然后解析模型的最优解，最后根据模型最优解确定问题的最佳方案。这三个环节逐步递进、由浅入深、由易入难，这启发我们采用一种渐进式的教学方法。

渐进式教学是一种应用较广的教学模式。文献调研显示，渐进式教学在初中物理教学、微生物实验教学、机械制图课程教学、国际贸易专业课程教学及在外科门诊临床实习教学等各层次、各类型的教学中都实现了良好的效果。渐进式教学的核心思想是循序渐进地引导学生对课程进行学习，最终实现良好的教学效果。“运筹学”遵循着“问题建模—模型解析—最优解反馈”的逻辑，因此非常适合于采用渐进式教学方法。

本文旨在为经管类专业“运筹学”教学探索一种“建模—解析—反馈”的渐进式教学方法。首先分析“运筹学”教学中存在的问题，然后探索一种“建模—解析—反馈”的渐进式教学方法以应对存在的问题，从而实现经管类专业“运筹学”的教学目标。

一、“运筹学”教学中的问题分析

笔者近年来为经管类专业学生讲授“运筹学”课程，通过观察和交流，发现学生在运筹学的学习中还存在以下突出问题。

第一，学生对“运筹学”的学习兴趣普遍不高。虽然“运筹学”对经管类专业学生是一门非常重要的课程，但在教学中发现很多学生没有对“运筹学”表现出很强的兴趣。通过与学生交流得知，很多学生感觉“运筹学”是一门偏数学的课程，与自己专业的关联性不是很强。事实上，由于“运筹学”涉及大量的数学优化问题，在一些学院被划归在数学学科之下。对于经管类专业的学生偏重数学解析的“运筹学”，自然难以引起他们的兴趣。因此，只有从实际管理问题出发引出数学模型，才能够激发他们的学习兴趣。

第二，学生对“运筹学”存在恐惧心理。“运筹学”模型解析以最优化理论作为基础，其中涉及大量的数学推导和计算。经管类专业学生大多是文科生，数学基础比较薄弱，很难轻易掌握其中的数学解析，从而产生恐惧心理。因此，在数学模型解析的教学中，教师需要倾注更多的心力，探索有效的方法，循循善诱。

第三，学生对模型最优解实际意义的认知不深。大多数学生在得到模型最优解后，通常不会去思考最优解的实际含义。模型最优解与实际问题最优方案之间存在一定距离，学生需要把最优解“翻译”成最优方案，这样可以帮助他们深入地认识“运筹学”。

为解决以上问题，在“运筹学”教学中应该首先以实际问题为牵引，讲授数学模型的构建，其次探索有效方法以讲授数学模型的解析，最后讲授模型最优解对于实际问题的反馈，即采用一种“建模—解析—反馈”的渐进式教学方法。

二、“运筹学”渐进式教学方法

“运筹学”渐进式教学遵循“建模—解析—反馈”三个递进的教学环节，如图1所示。首先从实际问题出发，讲授如何根据实际问题建立数学模型，其次讲授如何解析数学模型获得其最优解，最后讲授如何将模型最优解反馈到实际问题以得到最优方案。

图1 “运筹学”渐进式教学模式

（一）建模环节：从实际问题到数学模型

“运筹学”立足于解决实际问题。对于经管类专业的学生来说，只有让他们意识到“运筹学”在解决实际问题中的价值，才能激发他们对“运筹学”的学习兴趣。为此在每个分支教学伊始，选取一个实际问题作为引导案例。一方面引起学生对本分支的学习兴趣，另一方面让学生初步了解本分支将解决哪类问题。例如，在给经管类专业学生讲授线性规划时，笔者用某人力资源规划问题作为引导案例；在讲授运输问题时，用某汽车公司的生产基地与分销中心的运输问题作为引导案例。从课堂情况来看，学生表现出很强的兴趣。

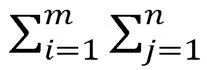
虽然不同的实际问题对应的数学模型不一样，但它们都是由决策变量、目标函数和约束条件三部分组成。因此，在讲授建模的过程中，着重培养学生的建模意识，以及正确定义决策变量和正确表示目标函数和约束条件的建模能力。

（二）解析环节：从数学模型到最优解

在建立数学模型之后，需要讲授如何解析数学模型以得到其最优解，这是最难的，也是最重要的一个教学环节。实际上，每类数学模型都有对应的优化方法。例如，线性规划模型对应单纯形算法，运输模型对应表上作业法，整数规划模型对应分支定界法或割平面法，最短路模型对应Dijkstra 算法或Floyd-Warshall 算法。这些方法的共同特点是既有逻辑步骤，每个步骤下又有具体操作细节。例如，分支定界算法的逻辑步骤是对线性规划问题进行反复的分支和定界，直至找到整数最优解，而如何分支和如何定界又是操作细节。

笔者在教学过程中发现，有些学生能够掌握方法的逻辑步骤，却在操作细节上不熟练；有些学生能够较好地掌握细节，却无法把握方法的整体逻辑步骤。因此，对于优化方法的教学应该使得学生既能把握方法的整体脉络，又能掌握具体的操作细节。在此目标下，对于每种方法可以绘制一个方法流程图，明晰该方法的整体逻辑步骤。例如，见单纯形算法的流程图图2。在讲解一种方法的过程中，采用该方法的流程图作为引导。即按照流程图一步一步地讲授，讲到每个步骤时跳到该步骤对应的操作细节进行详细讲解，讲完该步骤下的具体操作之后再跳回到流程图的下一步，依次往下，直至讲完方法。通过此方法让学生既能掌握方法的整体逻辑，又能掌握具体的操作细节。

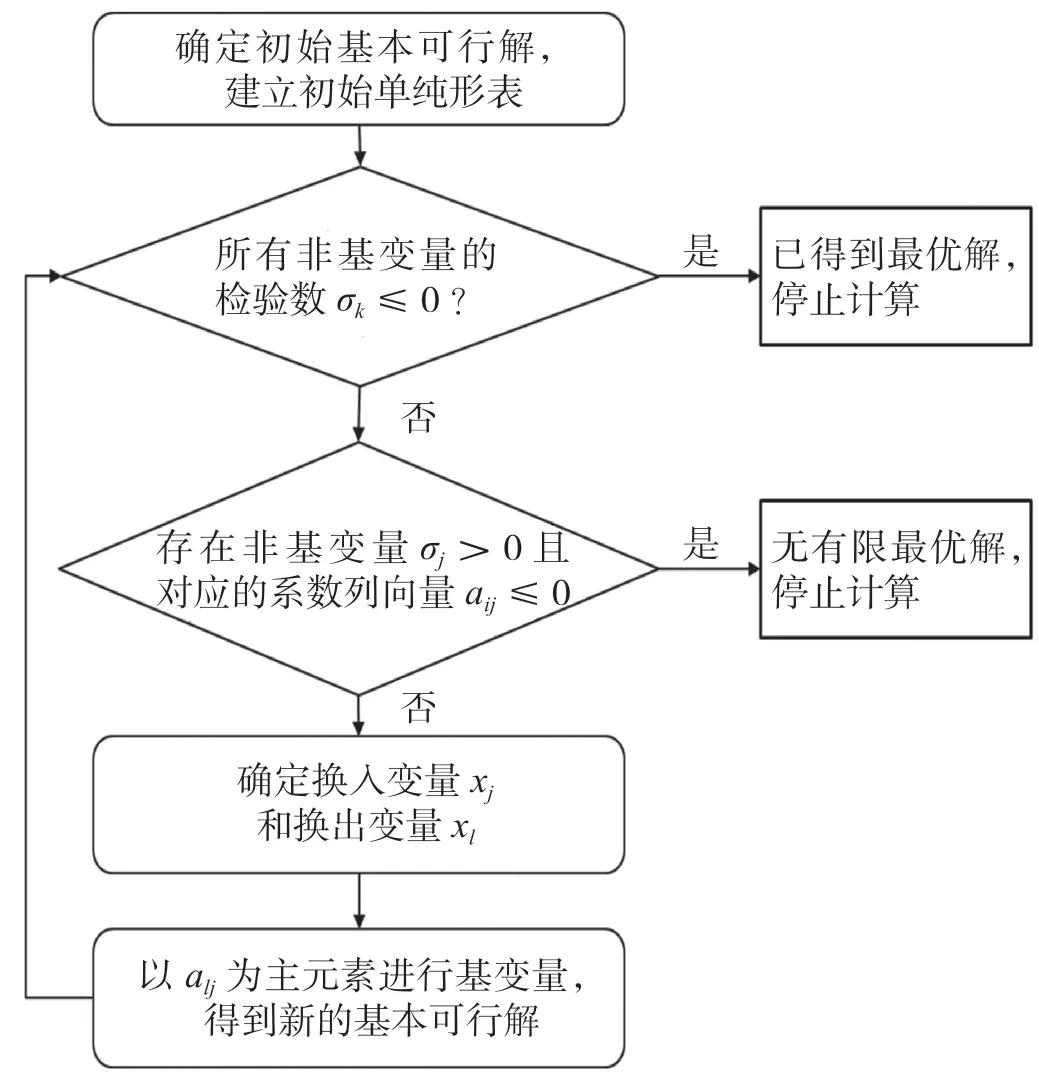
图2 单纯形算法流程图

（三）反馈环节：从模型最优解到问题最优方案

在获得模型最优解之后，需要将模型最优解反馈到实际问题，以获得实际问题的最优方案，形成一个教学闭环。这是最容易的一个教学环节，但也是不可或缺的一个环节，否则就无法形成教学闭环。在这个教学环节中，需要教授学生将模型最优解“翻译”成问题的最优方案。例如，生产计划问题最优解为X=（10，20，25，0，0），其对应的最优生产方案为生产A产品10件，生产B产品20件，生产C产品25件。X的最后两个分量等于0，表示松弛变量或人工变量取值为0，没有实际含义。又例如，表1所示为某运输问题的最优解。通过该最优解可知=5，=3，=1，=6，其余的x=0。根据该最优解，可得到最优运输方案为：从产地A运往销地B物资5个单位，从A运往B物资3个单位，从A运往B物资6个单位，其余产销地之间则不进行物资运输。注意到，虽然=1，但是由于B是虚拟的销地，因此实际上A并没有生产这1个单位物资，也就不会往B运输物资了。通过最后的反馈环节，使学生加深对模型最优解实际意义的理解，也加深对于运筹学思想的理解，有利于夯实学生对于“运筹学”的学习兴趣，进而提高运筹学的教学效率。

表1 某运输问题的最优解

结语

本文为经管类专业“运筹学”课程教学提出了一种“建模—解析—反馈”渐进式教学方法。该教学方法将“运筹学”教学划分为“数学建模”“模型解析”和“最优解反馈”三个环节。这三个环节层层递进，首尾相连，形成一个教学闭环。建模环节着重培养学生对实际问题建立数学模型的能力，解析环节重点培养学生熟练掌握各种优化方法的逻辑脉络和具体操作，而反馈环节则培养学生对于模型最优解实际意义的理解。通过该渐进式教学模式，激发学生学习“运筹学”的兴趣，培养学生数学建模能力，引导学生掌握各种优化方法，夯实学生对“运筹学”的理解，最终实现“运筹学”的教学目标。

在实施该渐进式教学方法的过程中也会遇到诸多问题。例如，如何根据学生的专业背景选择合适的实际问题，如何应对学生基础和学习能力的个体差异问题，以及如何在优化方法讲解中营造积极的学习氛围等。这些问题需要在教学的过程中得到有效解决，才能够保证该渐进式教学实现更好的效果。