基于时间成本的城市街道人行横道间距设置研究*

李 念 何烈云 裘煜杰

(浙江警察学院交通管理工程系 杭州 310053)

人行横道是城市中为满足行人过街需求而设置的最为普遍的过街设施，在道路交叉口处基本都会有所设置，而在2个交叉口之间的城市路段内，人行横道的设置往往只是基于规范[1]的粗略设置。

人行横道间距的设置需考虑到人车的过街需求及其对人车运行的干扰，国内外学者也主要是从这2个方面展开研究的。Kaseko等[2]从行人的角度出发，通过研究人行横道处行人在过街时的通行特性，得出单个人行横道对干道上行人过街交通流的影响。Bastian等[3]通过VISSIM对各种过街类型下非人行横道处、人行横道处车辆和行人的延误进行了模拟，得出了车流量与人车延误的关系，为人行横道的间距设置提供了参考。夏晶[4]综合分析了各种功能道路对安全、效率与稳定的不同要求，运用多目标决策方法，确定了各种道路条件下人行横道的合理间距。陆建等[5]通过对道路通行能力、行人心理等展开分析，提出平面行人过街设施合理间距的分析计算方法。郑长江等[6]分析了路段人行横道间距对人车混合交通流的影响因素，利用层次分析法计算得到路段人行横道的合理间距值。

综上所述，现有的研究有以下特点：①人行横道与人车交通的相互影响研究多集中在单个人行横道处，但实际中路段内一般存在多个人行横道；②对人行横道合理间距的研究方式较为单一，大多都是基于特定路段给出推荐值，且推荐值的适用范围及其合理性尚待验证；③人行横道间距设置时仅考虑满足行人交通，未考虑与机动车交通取得协调。本文的研究对象为城市路段中无信号人行横道的间距设置，通过对机动车与行人在无信号人行横道处的运行分析来建立行人和机动车总延误最小，即总时间成本最低的城市路段人行横道间距模型，为城市路段内的人行横道间距的设置与优化提供新思路，同时，对于降低人车延误，提高道路系统的通行效率也有着重要意义。

1 安全间隙和平均等待时间计算

等待双方可穿越安全间隙的出现是行人和机动车在无信号人行横道处通过的基本要求，而平均等待时间又是行人是否会违反交通法规横穿道路的重要评判指标[7]。在城市路段内，一般机动车交通量不会太大，车头间距能满足有一定间隙供行人安全穿越，故设置的人行横道多为无信号控制人行横道。

1.1 行人穿越机动车安全间隙

当行人处于人行横道线，准备穿越无信号灯控制的道路时，会对机动车道上的机动车距离、车速等进行判断，当车辆之间的车头时距达到了行人对于安全过街的要求，行人就会在车辆运行间隙中进行穿越。假设车辆随机到达且符合泊松分布，根据交通流的相关理论，可得车头时距符合负指数分布，且车头时距可满足行人穿越的概率为

P(hv≥αp)=e-λvαp

(1)

式中：hv为机动车的车头时距，s；λv为车辆在无信号人行横道处的到达率，pcu/s；αp为行人可穿越机动车的安全间隙，s。

由于行人过街要考虑到通过机动车道所穿越的时间，并且在启动前观察判断会有一定的启动损耗时间，因此行人过街可穿越机动车安全间隙αp的表达式为

(2)

式中：d为单车道宽度；vp为行人的过街速度；tr为行人观察损耗时间，通常取2 s；ta为车身通过时间，通常取标准小客车时间0.72 s[8]。

假设机动车高峰小时流量为Qs，则可得到行人的平均等待时间为

(3)

1.2 机动车穿越行人安全间隙

参照行人可穿越机动车的安全间隙计算方法，机动车可穿越行人的安全间隙，也就是驾驶员行驶到人行横道前，既要确保通过的机动车道上没有行人，也要确保前方人行横道上有行人突然闯入时能安全刹车，因此机动车可穿越行人安全间隙αv的表达式为

(4)

式中：ts为从驾驶员看到前方有行人至车辆安全刹车所需的时间。根据城市道路上机动车车速的具体情况，可以得到不同车速下安全停车时间ts的取值表,见表1。

表1 不同车速下安全停车时间取值表

2 人车运行分析及延误时间计算

忽略交叉口处人行横道的影响，假设行人和机动车到达符合泊松分布。根据前文分析可知，行人和机动车在无信号人行横道处的运行过程中，其中一方会产生聚积现象，直至流通的另一方出现可穿越安全间隙，方可开始消散。

2.1 行人与机动车的排队聚散过程分析

机动车和行人在无信号人行横道处的通行权利是交替的，类似于有受到信号灯控制，即人和车分别在不同的相位下运行，一方流通运行，另一方就需要排队等待，图1可以表示这一过程。

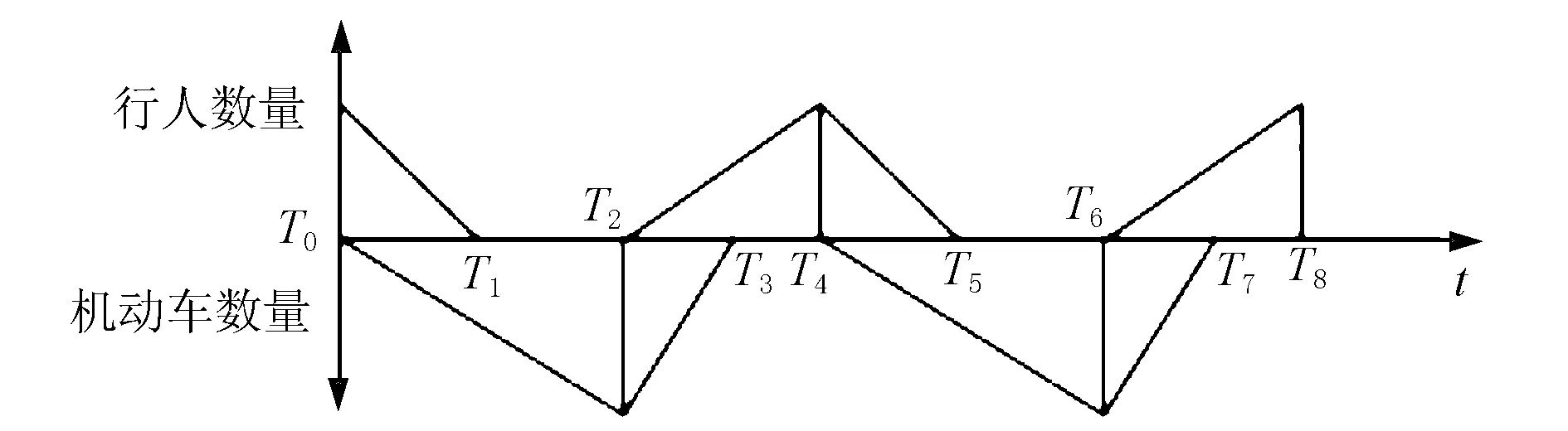
图1 聚积和消散示意图

图1中上下两部分分别表示行人和机动车在无信号人行横道处聚积与消散的情况。T0～T2时间段是表示行人通过、机动车排队的时间，用Tp表示；T2～T4时间段是表示机动车通过、行人排队的时间，用Tv表示；T0表示到达的机动车中首次出现行人可穿越机动车安全间隙的时刻，此时行人排队数量达到最大值，并立即通过人行横道开始消散。T1表示排队的行人消散完毕但尚未离开人行横道的时刻，此时后面的行人仍随机到达人行横道，机动车继续排队等候；T2表示行人中首次出现机动车可穿越行人安全间隙的时刻，此时机动车排队数量达到最大值，并立即开始以饱和流率开始消散；T3表示排队的车辆消散完毕，此时后面的机动车仍随机到达人行横道，行人继续排队等候；T4时刻与T0时刻相同，表示行人开始消散的时刻，之后人车又以该时刻为循环起点开始运行。

2.2 行人与机动车通行能力计算

为了便于分析，将T0～T1时间段记为Tp1，T1～T2时间段记为tp2，将T2～T3时间段记为tv1，T3-T4时间段记为tv2。

Pk=e-λvαp[e-λv(k-1)αf-e-λvkαf]

(5)

则在单位时间t内行人可穿越机动车的总数Np为

(6)

将式(6)除以t可得行人在人行横道处穿越机动车过程中的理论通行能力Cp,令z→∞可得

(7)

因机动车到达同样符合泊松分布，故同理可得机动车穿越行人过程中，机动车的理论通行能力Cv为

(8)

式中：αg为机动车连续通过C点的最小车头时距，一般采用2 s。

此外，将αg看作车辆运行的饱和车头时距，可得到车辆消散时的饱和流率sv

(9)

式中：n为车道数。

2.3 人车排队消散时间计算

行人消散时间tp1，包括排队行人总的跟随时距以及行人通过人行横道的时间。由于行人过街会有一定的空间需求，有研究表明行人过街的横向间距约为1.0 m[9]，依据《道路通行能力手册》[10]规定，以行人空间占有量为1.4 m2/人的D级服务水平来描述人行横道，则过街行人的前后间距为1.4 m，那么可得到

(10)

式中：tp1为机动车消散时间;vp1为行人过街时间；w为人行横道宽度。

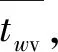
(11)

机动车消散时间tv1，也就是机动车在Tp和tv1时间段内到达的机动车总量饱和流率sv消散需要的时间，得到

(12)

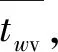
(13)

最终可分别得到机动车与行人运行的相位时长为

(14)

(15)

式中：Tp和Tv为2个未知量，其余参数均可通过实地调查获取。因此行人和机动车在无信号人行横道处的一个循环周期为

(16)

2.4 人车延误时间计算

行人的延误主要是行人在等待机动车过街至出现可穿越间隙时的排队延误，由此可以得到一个周期内排队的行人数量Np

Np=λp·Tv

(17)

可得在Tv时间段内(即图1中T2～T4)上半部分围成的三角形面积即为周期内排队行人的总延误Dp

(18)

行人在tp2时间段内随机到达不受机动车干扰的车辆数Np′

Np′=tp2·λp=eλpαv-1-λpαv

(19)

(20)

(21)

3 基于时间成本的路段人行横道合理间距模型及实例分析

人行横道间距的设置影响因素繁杂，为便于分析研究，建立如下假设：①在长度为L的路段内设置有多处无信号人行横道，人行横道间距相等且均为s；②两侧的人行横道设置位置距离两侧交叉口的距离小于s；③行人过街需求在两侧的人行道上均匀分布。人行横道设置基本情况见图2。

图2 人行横道设置示意图

3.1 模型建立

基于以上假设，可以得到路段内设置的人行横道总数为Nr=L/s-1，其中L/s无法除尽时，取值应向下取整。

由于行人过街需求均匀分布，所以行人从出发地到相应的人行横道绕行距离的平均值为s/2，而绕行所花费的时间也就是行人的延误时间。再结合上文对单个无信号人行横道行人平均延误的分析，可以得到路段内行人在单位时间T内的总延误时间为

(22)

式中：Qp路段内的过街行人流量；vp2为行人在人行道上的速度。

结合上文对单个无信号人行横道处机动车平均延误的分析，可以得到路段内机动车在单位时间T内的总延误时间为

(23)

式中：Qv为路段机动车的总流量。

机动车和行人的延误之和为

(24)

(25)

(26)

式(26)中求解出来的最小值为Dmin路段内行人和机动车总延误时间的最小值，这时人行横道间距的取值Sbest即为路段内人车交通系统时间成本最低的最优间距。

3.2 实例分析

研究时选取杭州市某路段作为人行横道间距设置的对象。该路段为双向六车道，内设有2处无信号人行横道，两侧均为居民小区，无特别的人流吸引点。基本情况见图3。

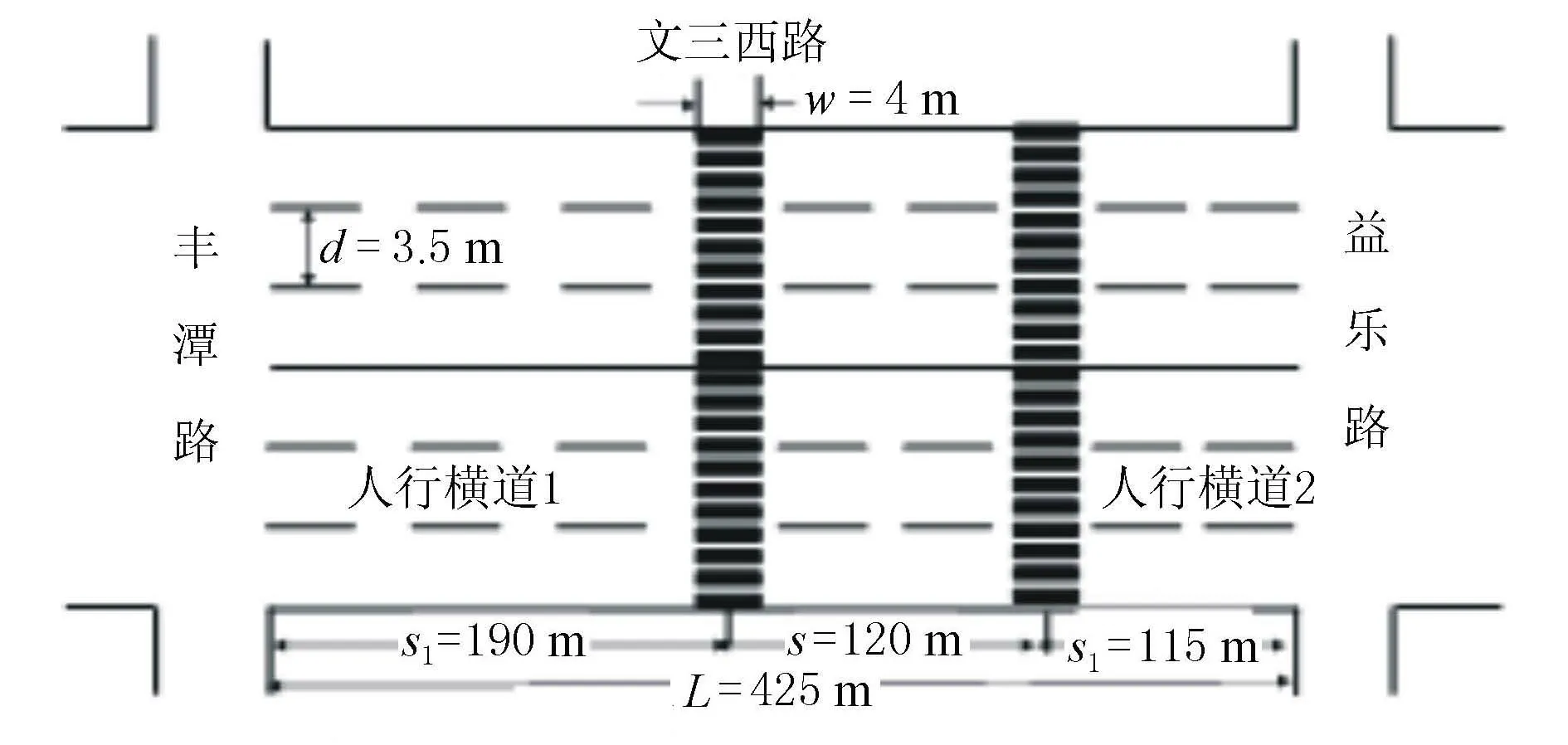
图3 杭州市文三西路路段人行横道设置基本情况

通过实地调查与数据计算，得到交通流基本参数见表2。

表2 交通流基本参数

选取无信号人行横道1，以20 s为调查间隔对人车的到达数作连续观测，经过统计概率模型对观测值进行拟合及拟合度检验，发现人车到达无信号人行横道用泊松分布拟合是可以接受的，适用于模型假设，其分布曲线见图4。

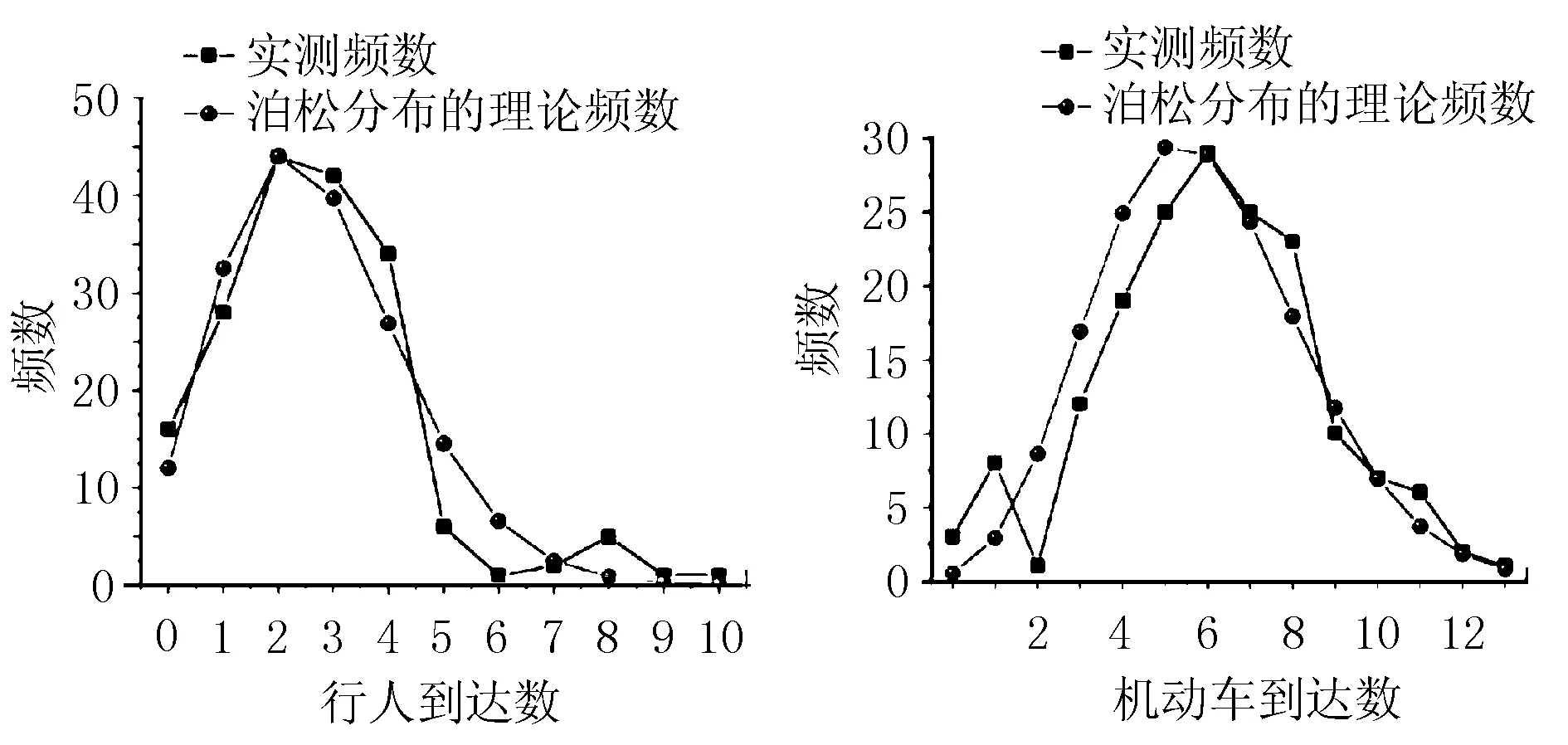
图4 泊松分布理论频数与实际频数分布对比曲线图

根据计算可得Sbest=84.45 m，Nr=3。而在实际中设置这3处人行横道时，由于路段内行人过街需求会有所差异，所以可优先设置其中一处在人流量相对较大的地方，再依次设置以此为基点的间距相同的另外两处。此外，靠近交叉口的两侧的人行横道在设置时，距离交叉口处人行横道的间距应小于求出的间距s，从而使实际情况更接近模型假设条件，得到更科学的结果。综上，优化后的人行横道间设置见图5。

为验证模型可行性，可通过优化前后的延误情况进行对比分析。将道路交通流基本参数分别代入式(24)，可得到优化前的人车总延误65 625 s，优化后人车总延误51 127 s，优化后的人行横道使得路段内人车总延误相比原来下降了20%。

图5 优化后的人行横道设置示意图

4 结论

1) 通过分析行人和机动车在单个人行横道处的运行规律，推导出行人和机动车在无信号人行横道处的延误模型，得到受行人与机动车到达率影响的每个行人或每辆机动车的平均延误。

2) 分析了行人和机动车在路段内受多个人行横道影响下的延误情况，在基于一定假设的前提下，推导出行人和机动车时间成本最低，即总延误时间最小的人行横道间距模型。

3) 通过实例分析，应用模型对实际的人行横道间距进行优化，并验证了模型能有效减少人车总延误，从而提高人车系统的总体效率。