玄武岩纤维混凝土弯曲疲劳性能研究*
白建文 赵燕茹 苏 颂
(1.内蒙古工业大学矿业学院, 呼和浩特 010051; 2.内蒙古工业大学土木工程学院, 呼和浩特 010051;3.长春工业大学人文信息学院, 长春 130122)
0 引 言
混凝土因其卓越的性能成为世界上应用最广泛的人造建筑材料。然而普通混凝土具有易开裂、抗拉强度低、韧性差、自重大等缺点,且随着建筑工程对混凝土材料各方面要求的日益提高,这些缺点限制着它优势的发挥。长期以来,国内外许多研究人员从提高混凝土材料自身性能的角度着手,对提高和改善混凝土的易开裂、抗拉强度低、韧性差等问题进行了大量研究,其中在混凝土中掺入不同类别的纤维制成纤维混凝土被认为是最有效的途径之一[1-4]。
玄武岩纤维具有良好的物理、力学性能,其优异的性能与混凝土复合可改善混凝土自身的缺点,提高混凝土的劈拉强度、弯曲强度以及弯曲韧性等力学性能指标。文献[5-7]进行了不同纤维掺量下的玄武岩纤维混凝土的抗压、抗弯以及劈裂抗拉强度试验;孟雪桦等对切口梁进行了三点弯曲试验研究了玄武岩纤维混凝土的断裂性能[8];Sim等研究了不同纤维掺量下玄武岩纤维混凝土的力学和变形性能[9];许金余等对玄武岩纤维混凝土的动态力学性能进行了试验研究[10-13]。然而迄今为止,对玄武岩纤维混凝土疲劳性能进行深入研究的文献还鲜有报道。
本文通过三点弯曲疲劳试验,对4种纤维掺量下的玄武岩纤维混凝土在3种不同应力水平下的疲劳性能进行了研究,对试验数据进行数理统计分析并拟合了疲劳方程;研究了玄武岩纤维混凝土试件的疲劳破坏机理,为玄武岩纤维混凝土性能研究、应用提供理论和试验依据。
1 试 验
1.1 试验材料
1)水泥:冀东牌P·O 42.5普通硅酸盐水泥,其化学组分及物理力学性能指标分别见表1和表2;2)粗骨料:直径为5~20 mm连续级配的碎石,含泥量0.8%;3)细骨料:天然河砂,细度模数为2.45,属中砂,级配良好,容重为1 673 kg/m3,表观密度为2 590 kg/m3,含泥量为1.9%;4)拌和用水:采用呼和浩特市自来水;5)玄武岩纤维:作为增强纤维,其物理、力学性能见表3。

表1 水泥的化学组分Table 1 The chemical composition of cement %

表2 水泥的物理力学性能Table 2 Physical-mechanical properties of cement

表3 玄武岩纤维物理、力学性能参数Table 3 Physical and mechanical properties of basalt fiber
1.2 配合比与试件制备
根据JGJ 55—2011《普通混凝土配合比设计规程》,混凝土设计强度等级为C40,水灰比为0.45,砂率为34%,玄武岩纤维体积掺量为0.0%、0.1%、0.2%、0.3%。试验制作尺寸为100 mm×100 mm×400 mm的棱柱体试件48根,用于静弯曲强度及弯曲疲劳性能的试验研究;制作尺寸为100 mm×100 mm×100 mm的立方体试件4组共12个,用于同条件下玄武岩纤维混凝土抗压强度的测试。试验中使用的混凝土配合比和及拌合物的工作性能、28 d龄期抗压强度见表4所示。
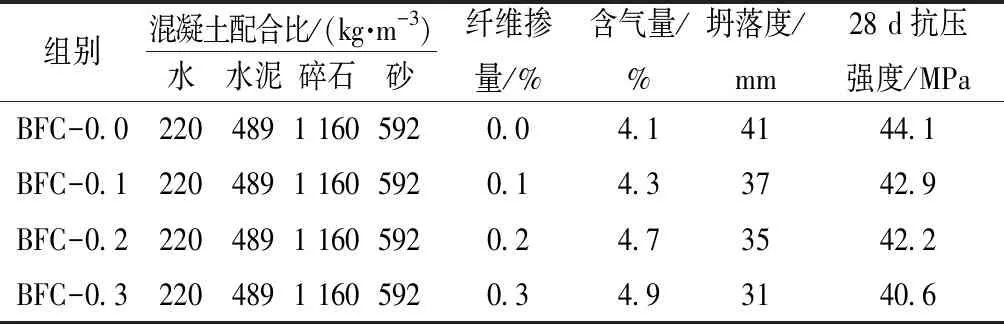
表4 混凝土配合比设计和工作性能Table 4 Mix proportion design and workability of concrete
搅拌时,采用先干拌后湿拌的搅拌方式。将河砂、碎石、水泥依次投入搅拌机中先干拌60 s,在继续干拌的过程中缓慢撒入玄武岩纤维后继续干拌120 s,然后加水搅拌180 s,使玄武岩纤维在混凝土混合物中充分搅拌均匀,装入试模后振捣成型。将试件保湿养护1 d后脱模,然后在温度为(20±2)℃、湿度不低于95%的标准条件下养护至28 d龄期后进行试验。
1.3 试验装置
疲劳加载系统使用MTS-793疲劳试验机,疲劳试验加载方式及位置如图1所示;采用正弦波等幅加载,加载频率为10 Hz,加载波形如图2所示。
2 疲劳试验结果分析
2.1 疲劳试验及结果
疲劳试验采用三点弯曲加载方式,弯曲应力以最大加载应力σmax、最小加载应力σmin之间采用无间隙时间的正弦波加载,荷载频率为10 Hz,以应力控制模式进行加载,应力水平S是实际加载应力σmax与静载弯曲强度σ之间的比值,分别取Smax=0.70、0.75、0.80,试验中最小循环应力取σmin=0.1σ,通过fmax=SFmax、fmin=0.1Fmax换算可知疲劳加载时最大、最小循环荷载值,具体加载数据、抗弯极限荷载、疲劳试验结果见表5所示。
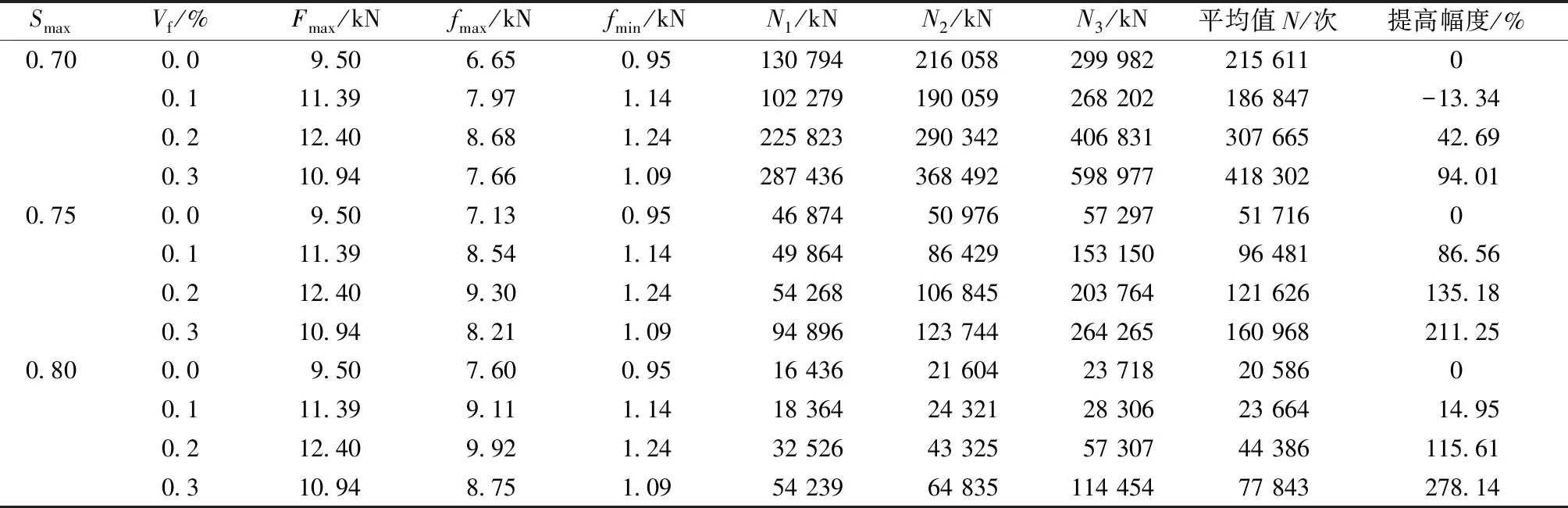
表5 玄武岩纤维混凝土疲劳寿命试验结果Table 5 Fatigue life data of basalt fiber reinforced concrete
2.2 纤维掺量对疲劳寿命改善效果
表5最后一列给出了相同应力比情况下不同掺量的玄武岩纤维混凝土试件与素混凝土试件相比平均疲劳寿命的提高程度。可以看出,仅纤维掺量Vf为0.1%、应力水平为0.7时,试件的疲劳寿命相比素混凝土略有下降,其余掺量的纤维混凝土试件的平均疲劳寿命均有不同程度的提高,且纤维掺量越大,平均疲劳寿命提高的幅度越大,说明玄武岩纤维对混凝土试件的疲劳寿命的提高有着不可忽视的影响。
2.3 纤维掺量与应力水平对疲劳寿命的影响
采用单因素方差分析(ANOVA)[14-15]也可以估计玄武岩纤维掺量对混凝土弯曲疲劳寿命的影响。在相同的应力水平下,比较了4种不同纤维掺量 (0.0%、0.1%、0.2%、0.3%)试样的疲劳寿命,方差分析结果如表6所示。可知:在应力水平为0.7、0.75时,相关的F值均小于在0.05下的标准值(F0.05(3,8)=4.07),说明此时玄武岩纤维掺量对弯曲疲劳寿命影响不显著;在应力水平为0.80时,相关的F值大于在0.05下的标准值,说明此时玄武岩纤维掺量对弯曲疲劳寿命影响是显著的。
3 疲劳方程建立
3.1 玄武岩纤维混凝土疲劳寿命的两参数威布尔分布理论
利用数理统计中数学概率模型的威布尔分布对材料的疲劳寿命进行统计分析成为近年来国内外常用的理论之一[16],被广泛地应用于疲劳寿命的统计分析中,可对材料在疲劳荷载作用下的安全寿命进行预测。

表6 疲劳单因素方差分析Table 6 Single-factor analysis of variance of fatigue life
在相同循环荷载作用下,混凝土试件疲劳寿命N的威布尔分布概率密度函数如式(1)[17]:
N0 (1) 式中:N0为最小寿命参数(即可靠度为100%的安全寿命);Na为特征寿命参数;b为威布尔形状参数(即斜率参数)。用符号Np表示威布尔分布的威布尔随机变量,并根据式(1)给出的概率密度函数可求得Np的分布函数F(Np),如式(2): (2) 根据数理统计分析理论,可靠度P的超值累积频率函数如式(3): P(N>Np)=1-P(N (3) 在已知b、Na、N0三个参数值的情况下,根据式(3)即可求出可靠度为P时的疲劳寿命Np。由于玄武岩纤维混凝土的离散性,本试验中统一取N0=0。则式(1)、(2)可简化为两参数的威布尔分布式: 0 (4) (5) 对式(5)取倒数,然后两边同时两次取对数得式(6): (6) Y=bX-β (7) 式(7)为直线方程的形式,在已知疲劳数据的情况下进行线性拟合,可求得b、β值。用于检验的试验数据是否服从两参数威布尔分布,如果试验数据线性回归结果较好,相关系数R2越接近于1,则证明该组试验数据越服从两参数威布尔分布假设,反之则不成立。 在给定应力水平下,对可靠度P可根据式(8)进行计算: (8) 式中:K为在一定应力水平下用于疲劳试验的试件个数;i为疲劳试件试验数据按照从小到大顺序排列的序数。 根据两参数威布尔分布理论以及弯曲疲劳寿命试验结果,得到玄武岩纤维混凝土试件在不同应力水平下疲劳寿命Ni与相应可靠度P之间的关系,见表7。同时,对表7中的数据作图并进行线性回归分析,由回归结果得到4种纤维掺量、3个应力水平下的线性回归系数b、β及相关系数R2,如图3所示。 由图3可以看出,普通混凝土和玄武岩纤维混凝土疲劳寿命数据点近似呈现直线分布,lnN与ln[ln(1/P)]之间线性相关性较好,大部分相关系数R2均能达到0.9以上,相关性显著,只有极个别由于样本空间容量小以及试件尺寸的特殊性,拟合度出现偏差,但是相关系数R2也达到了0.75以上,说明玄武岩纤维混凝土的弯曲疲劳寿命很好地服从两参数威布尔分布。即两参数威布尔分布可以用来描述玄武岩纤维混凝土的弯曲疲劳寿命。 表7 玄武岩纤维混凝土疲劳寿命的两参数威布尔分布检验Table 7 Two-parameter Weibull distribution test of fatigue life of basalt fiber reinforced concrete 图4为不同纤维体积掺量下玄武岩纤维混凝土威布尔分布形状参数和应力水平的关系。可知,对于素混凝土而言,随着应力水平的减小,其威布尔形状参数先增大后减小,表明素混凝土的弯曲疲劳寿命离散性先减少后增大,在应力水平为0.70时弯曲疲劳寿命离散性最大;对于掺加玄武岩纤维的混凝土来说,随着应力水平的减小,威布尔形状参数先减少后增大,表明玄武岩纤维混凝土弯曲疲劳寿命离散性先增大后减小,在应力水平为0.75时离散性最大。从总体来看,掺入不同掺量的玄武岩纤维后,在各级应力水平下混凝土的弯曲疲劳寿命分布更加均匀,离散性更小,抗弯疲劳性能明显高于素混凝土。 根据图3所得的两参数威布尔分布检验回归分析结果可知,玄武岩纤维混凝土的疲劳寿命符合两参数威布尔分布,失效概率p′=1-P(P为可靠度),如式(9);相应失效概率下的等效疲劳寿命见式(10)。 (9) (10) 将图3中求得的线性回归系数代入式(10),通过计算可以得出不同应力水平下给定失效概率玄武岩纤维混凝土的等效疲劳寿命,计算结果见表8。 表8 等效疲劳寿命Nf随失效概率p′变化Table 8 Equivalent fatigue life Nf varied with failure probability p′ 依据表8中的结果,在实际工程中就可以预测出相应应力水平下玄武岩纤维混凝土不同失效概率下的疲劳寿命。 在混凝土疲劳试验中,由于单对数方程无法计算低应力水平下的疲劳寿命,而通过建立双对数方程可以精确地对试验结果进行线性回归分析;另外,在实际工程中,通常需要考虑一定存活概率下的混凝土疲劳寿命,因此本文采用考虑高低应力比修正后的双对数弯曲疲劳方程(式(11))来分析玄武岩纤维混凝土的弯曲疲劳性能。 lgS=a-clgN (11) 式中:a、c为弯曲疲劳方程参数。a越大,弯曲疲劳方程曲线相对高度越高,混凝土抗弯曲疲劳性能越好;c越小,弯曲疲劳方程曲线越陡,混凝土弯曲疲劳寿命对应力水平的变化越敏感。 疲劳方程曲线是在考虑不同失效概率的情况下绘制得到的S-N曲线。工程上通常给出的S-N曲线一般可理解为失效概率为50%时的S-N曲线[18]。根据表8得到的不同应力水平、不同失效概率下的等效疲劳寿命绘制失效概率p′为50%时的玄武岩纤维混凝土弯曲疲劳S-N方程曲线,如图5所示。 可以看出,拟合曲线近似为直线,各条直线的相关系数R2较高,均接近1.00。说明双对数疲劳方程能较好地反映玄武岩纤维混凝土应力水平S与疲劳寿命N之间的关系。在相同的应力水平下,随着纤维掺量的增加,曲线的a值均呈现增加的趋势,说明随着玄武岩纤维掺量的增加,弯曲疲劳寿命不断提高;而曲线的c值随着纤维掺量的增加呈现降低的趋势,说明纤维掺量越大,弯曲疲劳寿命对循环应力水平变化越敏感。 由图5可拟合得到,失效概率为50%时弯曲疲劳方程: vf=0.0%,lgS=0.146 4-0.056 8lgN,R2=0.98 (12a) vf=0.1%,lgS=0.204 7-0.067 7lgN,R2=0.93 (12b) vf=0.2%,lgS=0.223 6-0.069 0lgN,R2=1.00 (12c) vf=0.3%,lgS=0.285 2-0.078 6lgN,R2=0.99 (12d) 1)在相同的应力水平下,随着纤维掺量的增加,玄武岩纤维混凝土的平均疲劳寿命呈现逐步增加的趋势;玄武岩纤维的掺入,使得试件的弯曲疲劳寿命分布更加均匀,离散性更小,抗弯疲劳性能更好。 2)应用统计学理论对玄武岩纤维混凝土弯曲疲劳结果进行了统计分析,发现玄武岩纤维混凝土的弯曲疲劳寿命较好地服从两参数威布尔分布。 3)建立了玄武岩纤维混凝土在弯曲应力作用下的双对数疲劳方程。
3.2 玄武岩纤维混凝土疲劳寿命的两参数威布尔分布检验

3.3 等效疲劳寿命

3.4 弯曲疲劳方程
4 结 论

