中低层住宅建筑形态气候适应性优化设计策略研究
李智兴 潘鑫晨 董庆鑫
(1.浙江工业大学设计与建筑学院, 杭州 310023; 2.天津大学建筑学院, 天津 300072;3.沈阳理工大学建筑系, 沈阳 110159; 4.首都师范大学美术学院, 北京 100048)
建筑能源浪费是当今世界面临的主要挑战之一,建筑行业的能源消耗占大多数国家能源消耗总量的40%,相关排放量占温室气体排放总量的40%,2012年建筑行业产生了65.26亿t二氧化碳量。在过去二十年(1984—2004),主要能源消耗增长了49%,二氧化碳排放量增长了43%,平均每年增长2%和1.8%,近年来世界各国相继提出了建筑节能的规范与目标。大量既有研究表明设计阶段对建筑节能的实现具有重要意义,而大部分建筑设计师缺乏在项目前期设计阶段进行建筑节能评估与预测的有效手段,由此极大地限制了近零能耗建筑的发展。方案设计阶段与后续阶段对于节能设计的关注重点是不同的,前期方案设计阶段更关注建筑与环境因子之间的交互和影响,设计阶段越靠前,建筑与环境交互的设计因子越容易调整,而每个因子的调整都会对建筑的环境效益产生巨大的差异。研究以住宅建筑为例,重点讨论如何在方案阶段有效利用建筑参数化分析手段实现建筑气候适应性设计,在提高光环境舒适度的同时,节约建筑能耗。研究以此为技术手段,分析不同气候区典型城市的最优节能设计参数。
1 基于多目标优化的建筑气候适应性设计研究
1.1 建筑气候适应性设计研究综述
建筑气候设计就是要求在建筑设计过程中,通过尽可能利用自然条件解决建筑的热环境问题,提出相应的建筑技术手段和控制方法,达到对自然的尊重,以营造符合现代社会要求的更舒适、更健康的空间环境,从而成为真正人性化的建筑。建筑气候适应性设计需要考虑到建筑微环境的气候调节,利用自然手段减少建筑对于人工空调系统的依赖。在传统建筑技术的限制下,人们只得依靠被动式技术,如寒冷地区使用紧凑的室内空间布局、厚重的外墙等方法,湿热地区使用通透的建筑形式、较大的开窗来实现舒适的室内湿热环境。而现代建筑由于空调设备等环境调控技术的发展,使得人类可以更为主动且精确地控制室内环境,由此导致人们更依赖于人工设备来实现舒适的生活环境,从而割裂了建筑与气候的关系,消耗了大量的化石能源。针对这一问题,大量研究人员开展了建筑气候适应性设计的相关研究。
1953年,美国建筑师V·奥格雅首先提出的建筑气候分析方法,倡导建筑师在建筑设计中利用被动式手段调节建筑的微气候,其中最重要的一项即包括建筑的热环境。1963年,V·奥格雅出版了《设计结合气候》提出建筑设计应从人体的热舒适出发,考虑建筑对气候的调节作用,并采取被动式的设计方法,最大限度地利用太阳能、风能等可再生能源,降低建筑能耗[1]。1976年,Givioni出版了专著《人、气候和建筑学》[2],他改进了奥格雅的生物气候分析方法,提出根据气候环境和建筑热舒适性进行设计策略的方法,并将该方法命名为建筑生物气候设计法,与奥格雅的方法进行区分。
近年来,国外对建筑气候适应性设计的研究文献更为丰富。例如Alsousi对加沙这一地区进行了建筑的气候适应性研究,从热舒适性和能耗这两个方面对12座高层住宅进行了调查[3],研究人员最终发现:建筑在夏季的大部分空调能耗是由于墙壁,窗户和屋顶产生的巨大热量所导致的,此外,居住者、日常生活设施和空气渗透也会导致建筑能耗增加,但是对环境的热工性能和住户的舒适性影响相对较小。Enedri等对巴西南部多层住宅楼的热工性能进行了检测,他们记录了两个楼层,四个方向的八间卧室的热工性能,研究使用不同的变量来检查各种因素,例如表面颜色、窗户阴影以及墙壁和窗户的热工性质[4],最终得出结论:围护结构传热系数和建筑立面面积对最高温度的影响最大,需要尽量减小以改善夏季的室内热环境,而热容量和热时滞这两个变量,与最低气温的相关性最强,因此应该最大化以改善冬季的热环境舒适度。Virgilio等基于柯本气候分区,探讨了气候变暖对欧洲19个不同城市住宅建筑的影响程度[5],得出结论:2050—2080年平均气候温度的逐步提高将导致住宅建筑采暖能耗的降低,以及供冷能耗和二氧化碳浓度的增加,而环地中海气候区的城市受全球供暖的影响要高于欧洲内陆城市,通过提高建筑物的能源效率可以缓解这一趋势。Fatima等根据柯本气候分区,在全球范围内选择25种不同气候区下的典型城市,进行住宅建筑的被动式设计模拟分析与优化,以建筑生命周期成本(LCC)和建筑的供冷和供暖能耗为目标函数,对不同城市住宅建筑的性能进行了对比,并提出了相应的节能设计策略[6-7]。Jürgen等以叶卡-特林堡、东京、上海、拉斯维加斯、阿布扎比和新加坡为代表,使用相同的典型分析模型,进行被动房设计策略的分析与对比,包括围护结构的设计、气密性、冷却盘管的操作、热回收设备和送风温度等,最后针对分析城市提出了相应的被动房设计指导准则[8]。Letizia等选择了6个意大利城市作为代表,包括奥斯塔、米兰、坎波巴索、佛罗伦萨、莱切、卡塔尼亚,利用每个城市近30年的气候数据,分析了高宽比例等庭院类型参数对不同气候区下各城市建筑庭院湿热舒适度的影响[9]。
随着国内对建筑气候适应性设计的深入研究,人们对这方面的理解和认识也在逐步深化。杨柳利用生物气候图表的方法,探索了我国不同气候区的建筑热环境适应性设计原则,基于我国18个城市最近30年的主要气象参数的统计分析,建立了我国典型城市的建筑气候分析图,定义了不同城市被动式设计方法的边界气候条件[10]。茅艳针对我国的气候特点,首次在全国主要自然地理区域(包括四个气候区)进行了大量的室内热舒适现场调查与测试,得出了不同气候区12个典型城市的室内物理环境参数、主观热感觉、热舒适计算指标等主要参数;此外,她还结合我国气候特征,确定热舒适与气候环境之间的关系,研究限制人体热舒适适应性行为的影响因素,统计分析了我国各气候区人体热舒适适应性行为[11]。杨鸿玮提出了耦合风、光、热环境的既有建筑绿色化改造设计的方法,在研究绿色化设计影响因素的基础上,提出了相应的形式、构造、系统和设备的改造优化策略,扩充寒冷地区改造策略框架下适用的具体措施[12]。江亿提出了绿色住区的设计理念,从室内外多个不同的层面研究了城市住区的微气候和热环境[13]。刘加平等根据黄土高原地区的气候特点,提出了当地聚居建筑的基本形态,即新型阳光间式窑居太阳房,同时针对陕南山地气候和当地民居的基本状况,提出了被动式太阳能、生土围护结构与自然通风相结合的设计思路[14]。
国内外基于建筑设计的视角针对住宅建筑气候适应性设计问题的研究呈现出随时间发展逐步深入和细化的趋势,体现为以下特点:
1)建筑节能设计从传统的定性分析、理论研究和案例归纳总结逐渐转化为基于建筑物理和数学原理的性能模拟量化计算,使得建筑节能分析更具有学理性。
2)与建筑能耗相关的环境性能耦合性研究越来越多,较早文献大多仅讨论建筑设计及运行过程中的主被动式能耗,而随着当前研究的逐步深入,很多学者意识到建筑的节能分析不能以住户居住的舒适度及满意度为代价,因此研究重点逐步转移到建筑能耗与室内光热舒适度等其他因素的综合性评估系统上。
3)由于当前研究对于建筑能耗及环境耦合因素的关注逐渐增多,建筑节能设计的评价指标更为多元化,因此涉及到建筑节能设计的分析变量也在逐渐扩展,多个设计变量的组合共同作用于最终的节能设计目标,构成一个系统性的节能设计评价过程。
4)随着计算机技术的不断发展,与建筑参数化和环境性能模拟相关的新工具不断涌现,其他相关技术例如AR/VR、智能建筑控制系统等也在逐渐成熟,由此带来的研究方法、研究目的和研究对象逐渐多样化,与此同时,建筑性能模拟的数据量也越来越大。
然而目前国内外建筑师在设计初期由于面临诸多技术限制,以及缺乏系统性的方法,导致其对建筑气候适应性的分析不够重视,并且缺乏在设计的前期阶段对建筑节能预测的意识。当前研究仍在更加关注建筑设备的优化,而忽略了在初始设计阶段诸如建筑空间形式等被动设计参数对节能的影响。此外,建筑参数化集成式模拟可以作为建筑光热环境与能耗统筹分析的手段,有效辅助建筑师在方案阶段实现对目标的定量化评估及设计参数的寻优。因此,本研究利用我国各气候区典型城市的气象参数,对建筑形态的气候适应性设计参数进行光环境舒适度和建筑能量需求的优化搜索和对比,梳理了方案阶段主要关注的建筑形态节能设计参数。
1.2 多目标优化的定义
针对中低层住宅建筑气候适应性设计,研究提出利用基于建筑环境模拟的优化搜索方法,基于建筑模拟工具建立蒙特卡洛模拟框架(统计试验方法),来对输入参数进行不确定性分析与搜索,利用自动化手段来解决了传统意义上难以确定输入参数的问题。优化是在满足给定限制条件的情况下,寻找不同解决方案最佳组合的过程。执行优化需要决策变量,目标函数和约束条件,式(1)表达了一般数学意义上的优化过程。
minx∈Rnf(X)
(1)
式中:X为不同决策变量;f(X)为目标函数,约束条件为gi(X)≤0,i=1,2,…,m和lj(X)=0,j=1,2,…,p。
确定决策变量,目标函数和约束条件是优化过程中最重要的部分,根据不同的目标函数和约束条件分类可以选择不同的优化算法。
本研究基于Rhino/Grasshopper参数化平台,使用Ladybug与Honeybee环境分析插件,进行建筑环境与能耗建模分析。该工作流程的应用如图1所示。作为Grasshopper插件的Ladybug和Honeybee是支持环境设计的免费计算机应用程序,它们将3D计算机辅助设计(CAD)接口连接到经过验证的模拟引擎EnergyPlus中,来模拟建筑物的供暖、供冷、照明、通风和其他能量流以及湿度。
2 多目标优化平台的搭建
2.1 研究对象的确立
我国地处太平洋西岸,气候主要受季风环流的影响,又因地势的多变而复杂。我国在1993年颁布的GB 50176—93《民用建筑热工设计规范》中,根据全国各地最冷与最热月的平均温度,将全国分为7个一级建筑气候区和20个二级建筑气候区,一级区反映全国建筑气候上大的差异,二级区反映各大区内建筑气候上小的不同[15]。
研究根据我国建筑气候分区,从气候区Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ中选取了5个典型城市,分别为哈尔滨(严寒地区Ⅰ)、北京(寒冷地区Ⅱ)、上海(夏热冬冷地区Ⅲ)、深圳(夏热冬暖地区Ⅳ)和昆明(温和地区Ⅴ)。
我国以秦岭淮河为界对供暖区域进行划分,秦岭淮河以北地区在每年11月15日左右开始集中供暖并持续4个月到来年3月15日左右结束,部分地区(如哈尔滨等北方城市)由于气候原因会延长供暖时间,而秦岭淮河以南地区目前则没有集体供暖措施,但部分社区会根据实际需要进行供暖。根据目前各城市的实际供暖情况调查,列出了典型城市的供暖时间,如表1所示。

表1 根据建筑气候分区选取的典型城市Table 1 Typical cities selected accordingto building climate zones
2.2 优化目标的确立
2.2.1建筑光环境舒适度指标
依据本研究特点,即利用光环境评价指标作为优化的目标之一,与建筑全年供冷供暖需求及其他相关目标进行耦合分析。本研究使用全年有效天然采光照度(UDI)作为光环境优化的指标。UDI指标主要用于评价室内空间动态采光质量,并考虑到了某一时间室内工作面实际照度超过设计照度并可能引起眩光的部分,该指标表达的是一个范围值,在这个范围内,认为室内工作面照度水平满足要求。Nabil等在2005年提出有效照度范围值为:100 lux 2.2.2建筑能量需求的量化计算 建筑物的年度能量需求定义为所有公寓的供冷和供暖负荷之和,其余家庭热水、电器设备等能量需求均不计算在内,夏季供冷时间和冬季供暖时间根据不同气候区的要求设定。本研究中将空气调节系统(HVAC)性能系数假设为1,因此能量需求可以直接从模拟中提取EnergyPlus的结果。根据供暖与供冷设定点温度确定能量需求计算的参数,假设在HVAC系统中没有实施热回收装置。因此,年度建筑能量需求的目标函数可以通过式(2)计算: (2) 式中:BED为单位建筑面积年度建筑能量需求,kW·h/m2,建筑能量需求的计算仅考虑供暖和供冷需求,不考虑照明等其他方面;Eci为建筑第i层的供冷需求;Ehi为建筑第i层的供暖需求;n为建筑的总楼层数;A为建筑空调区的各楼层总面积。 为了尽可能多地考虑到住宅社区内不同的建筑形态组合方式,研究对住宅楼的长度、宽度和高度等相关参数进行了控制设定,间接地影响了住宅楼的体形系数、楼间距和容积率等相关参数。表2、表3列出了建筑形态优化涉及到的相关设计参数,这些参数共有26万种不同的组合方式,对应了26万种不同的建筑形态可能性,而研究依据前文设定的5个不同气候类型的典型城市,从这26万种建筑形态中,针对每个城市搜索到相应的最优设计参数并进行对比。 表2 建筑形态的优化设计直接控制参数设置Table 2 Direct control parameter settings for building form optimization 表3 建筑形态的优化设计间接控制参数设置Table 3 Indirect control parameter cettings for building form optimization 表2、表3建筑形态设计参数的不同组合会产生258 048种变化,部分模型如图2所示,本节以建筑能量需求和底层光环境舒适度最优为目标值,来针对各典型城市选取最为适合的建筑形态,并基于模拟数据来分析相应的气候适应性设计规律。 人工神经网络(ANN)通常称为神经网络,是模仿人类大脑结构和功能而构成的信息处理系统[17-18]。其中,BP神经网络(Back Propagation Neural Network)是一种按照误差逆向传播算法的多层前馈神经网络,由信息的正向传递和误差的反向传播两部分组成。在正向传播过程中,通过样本的训练与测试,输入信息通过输入层到隐含层,以及隐含层到输出层之间的权值或阈值逐层进行计算,结果传向输出层,如果输出层的结果与实际值的偏差在误差范围之外,则计算输出层的误差变化值;然后进行误差的反向传播,通过网络将误差信号沿原来的连接通路反传,从而调整各层神经元的权值,由输出层到隐含层,隐含层到输出层逐层进行计算,信息的正向传递与误差反向传播这两个过程反复进行,直到BP神经网络的预测值能够准确反映实际情况的结果为止,具体结构详见图3所示。 本文建立的神经网络模型考虑到建筑形态设计因素,输入神经元包括建筑体形系数、不同建筑之间的间距、建筑长宽比以及建筑朝向等设计参数,依据所建立典型模型的模拟结果做为数据库基础,对每个城市选取10 000组数据作为样本集训练预测模型。模型的输出神经元参数为2个,即建筑单位面积的全年能量需求和室内光环境舒适度UDI=100~2 000 lux的全年百分比。根据网络模型的输出参数(2个)和输入参数(9个),建立一个三层神经网络模型,如图4所示。 研究并没有单独为每个地区建立一个神经网络预测住宅室内空间对能耗以及采光的影响,而是把地区做为神经网络的输入数据之一,针对每个城市进行了大约10 000次随机模拟,模拟所使用的设计参数均匀覆盖了各自的取值范围。与分别建立不同的神经网络模型相比,这样能够在保证预测准确性的前提下,大幅减少训练神经网络所需的数据量,进而节省模拟时间。为了防止神经网络过拟合,研究采用交叉验证的方法,按照8∶2的比例划分为训练集和测试集。其中训练集有超过40 000条数据,测试集有超过10 000条数据。训练前,为了加快神经网络的收敛和提高预测的准确性,研究对数据进行了归一化的预处理。训练神经网络模型时,当模型如均方根误差等指标趋于稳定时,则可认为模型已经达到收敛。若误差足够小,则说明神经网络的预测效果良好,可以替代建筑模拟作为多目标优化中的适应性评估。表4中显示了神经网络模型在训练集以及验证集上的表现,结果显示:神经网络的误差已控制在一个可以接受的范围。为了直观展示神经网络模型的预测能力,研究从测试集中随机挑选了100条数据与神经网络的预测结果进行比对,结果如图5~图7所示。 表4 神经网络预测模型拟合度指标Table 4 Fit indexes of neural network prediction model MAE:平均绝对误差;MSE:均方误差;R2:判定系数。 研究基于预测模型生成的数据,使用IBM SPSS Statistics 24来分析参数与建筑物能量需求之间的斯皮尔曼(Spearman)相关系数,由于参数与建筑物能量需求之间的关系不是线性的,因此斯皮尔曼相关系数可以准确反映两组数据之间的相关性。相关分析结果显示在表5~表9中,斯皮尔曼相关系数在0.8~1.0范围内具有高相关性,在0.6~0.8范围内具有强相关性,在0.4~0.6范围内具有中等相关性,在0.2~0.4范围内为弱相关,在0~0.2范围内为极弱的相关性。从表中可以看出各典型城市住宅建筑的正立面长度和长宽比例对于目标函数有中等影响强度,斯皮尔曼系数多位于0.5附近及以上;哈尔滨和北京气候条件下,标准层层高对于总能量需求的影响适中,分别为0.577和0.474,但对于光环境舒适度的影响较弱,上海、深圳和昆明气候条件下,标准层层高对于总能量需求的影响相对于哈尔滨和北京较弱,基本介于0.2~0.4之间;各典型城市住宅的楼层数和建筑朝向对于目标函数的影响性很弱,仅深圳和昆明地区的住宅楼层数对于建筑总能量需求有弱相关性,分别为0.231和-0.209;此外,窗户形态参数对于目标函数的影响总体上来说不强,斯皮尔曼系数大多处于0.1~0.2之间。 表5 哈尔滨建筑形态设计参数的斯皮尔曼系数对比Table 5 Comparison of Spearman coefficients of building form design parameters in Harbin H:供暖耗能;C:供冷耗能。 研究通过参数化性能模拟并利用SPEA-2算法对所有设计参数进行优化,获得了最佳方案,如图8所示,色度最深的部分为帕累托前沿。表10和表11列出了不同气候条件下各城市在建筑能量需求最优(即BED最小,nZEB)和光环境最优(即有效天然采光照度UDI=100~2 000 lux的全年时间百分比最大,条件下的设计参数取值以及相应的优化目标结果,这些参数的建筑形态与图9~13逐一对应。 表6 北京建筑形态设计参数的斯皮尔曼系数对比Table 6 Comparison of Spearman coefficients of building form design parameters in Beijing 表7 上海建筑形态设计参数的斯皮尔曼系数对比Table 7 Comparison of Spearman coefficients of building form design parameters in Shanghai 表8 深圳建筑形态设计参数的斯皮尔曼系数对比Table 8 Comparison of Spearman coefficients of building form design parameters in Shenzhen 表9 昆明建筑形态设计参数的斯皮尔曼系数对比Table 9 Comparison of Spearman coefficients of building form design parameters in Kunming 从表10中可知,各典型城市nZEB节能最优的建筑正立面长度均为28 m,而除了哈尔滨以外各城市住宅建筑UDI最优的正立面长度为16 m,哈尔滨住宅建筑UDI最优的正立面长度为20 m。从各典型城市住宅建筑的长宽比例上看,除昆明以外各典型城市住宅建筑nZEB最优的长宽比例均为1,而昆明气候条件下住宅建筑nZEB最优的长宽比例为2;此外,各典型城市住宅UDI最优的长宽比例均为2,因为建筑平面的长宽比例为2时,建筑底层的光照条件更好。各典型城市住宅最优解的楼层数也不同,哈尔滨住宅nZEB最优解,深圳住宅的UDI最优解,以及昆明住宅的nZEB和UDI最优解的建议层数均为7层;而哈尔滨和北京住宅的UDI最优解建议层数为6层;其余典型城市的最优解层数均为3层。就标准层层高而言,多数城市的最优解层高为2.7 m,但是哈尔滨、深圳和昆明的UDI最优解分别建议采用3.3,3,3.3 m的层高来满足建筑底层最优的光环境舒适度。根据表中各典型城市建筑朝向的最优解可以看出,当建筑长宽比例不为1时,仅哈尔滨和深圳的UDI最优解分别建议朝向为90°和-45°,其余情况各典型城市的住宅最优解均建议朝向为0°(当长宽比例为1时,90°与0°重合)。通过各典型城市住宅最优解的窗墙比参数可知,除了昆明住宅nZEB和UDI最优解,其余城市住宅大多对于东立面、南立面和北立面的窗墙比要求大于对西立面窗墙比的要求,而昆明的住宅建筑希望西立面的开窗高于东立面和南立面,例如该地区nZEB最优解建议西立面窗墙比为0.35,但是东立面、南立面和北立面的窗墙比为0.25;而该地区的UDI最优解建议西立面窗墙比为0.45,但是东立面和南立面的窗墙比分别只有0.35和0.25。 表10 典型城市的建筑形态优化设计参数Table 10 Optimized design parameters of building form in typical cities nZEB*:全年能量需求最佳解决方案;UDI*:有效天然采光照度100~2 000 lux的全年时间百分比最佳解决方案。建筑正立面长度、标准层层高、建筑宽度单位为m。 表11 最优解的性能指标Table 11 Performance indicators of the optimal solution 总体上来看,各典型城市住宅建筑nZEB最优解的体形系数相对于UDI最优解偏小,而容积率相对于UDI最优解更大。这是由于在建筑物各部分围护结构传热系数和窗墙面积比不变的情况下,通常建筑能耗随体形系数的增大而增大,即体形系数越小则意味着建筑外表面面积越小,也就是能量流失途径越少,越具有节能意义。而UDI最优解更多考虑了住宅建筑底层的光环境舒适度,因此从节能效果上来说不如nZEB最优解。 从表11的最优解性能指标的对比可以看出,各典型城市住宅建筑的nZEB最优解和UDI最优解的总能量需求差异较大,且均为2倍左右,即UDI最优解的总能量需求普遍是nZEB最优解总能量需求的2倍,例如哈尔滨住宅的UDI最优解的总能量需求高于nZEB最优解73.3 kW·h/m2,北京住宅的UDI最优解的总能量需求高于nZEB最优解41.9 kW·h/m2,这说明通过建筑形态的调整,各典型城市住宅建筑的节能有很大的提升潜力和空间。在各城市中,哈尔滨住宅建筑的供暖需求改善潜力较大,该地区nZEB最优解相比较UDI最优解的供暖需求降低了62.1 kW·h/m2;而深圳住宅建筑供冷需求改善潜力较大,该地区nZEB最优解相比较UDI最优解的供冷需求降低了70 kW·h/m2;而其余各城市供暖和供冷需求的改善潜力相比哈尔滨和深圳较为适中。对比住宅底层光环境舒适度可以发现,各典型城市住宅建筑两种最优解的全年有效天然采光照度(100~2 000 lux)占全年时间的百分比差距也较大,例如哈尔滨住宅UDI最优解的全年有效天然采光照度百分比高于nZEB最优解36.6%,深圳住宅UDI最优解的全年有效天然采光照度百分比高于nZEB最优解28.4%。由此可见住宅建筑光环境舒适度的改善在一定程度上是以建筑总能量需求的增大为代价的,建筑师在进行设计决策时,需要考虑到不同利益方对于目标指标的需求,对不同利益方的设计要求进行权衡。 研究通过对住宅建筑形态参数,如建筑长宽比例、体形系数、社区容积率等参数的优化模拟,分析了5个典型城市不同气候条件下,节能最优和底层光环境舒适度最优情况下的设计参数及参数变化对于目标函数的影响趋势。在此基础上,研究从节能最优和底层光环境舒适度最优两个方面,得出各典型城市住宅建筑的总能量需求(包括供暖和供冷)以及底层全年有效天然采光照度百分比。从设计参数和性能指标两个方面分析了各典型城市住宅建筑气候适应性设计的特点,并提出建筑师应该根据气候特点以及不同利益方的需求进行设计决策。2.3 建筑形态参数的设置


3 典型城市住宅建筑的模拟优化分析
3.1 基于人工神经网络的预测模型建立
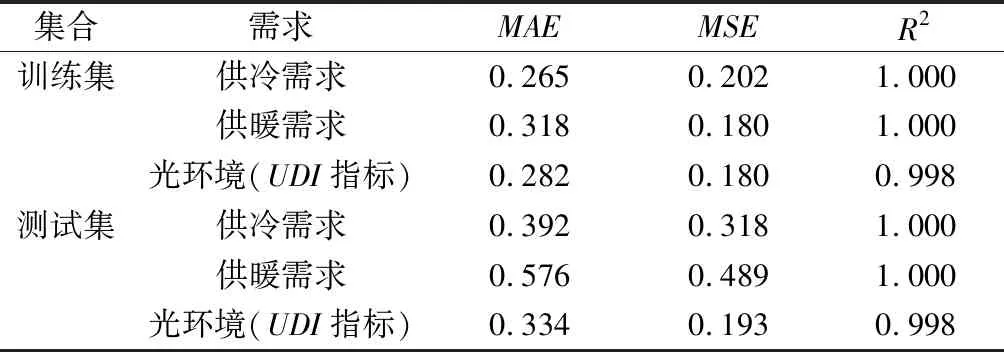
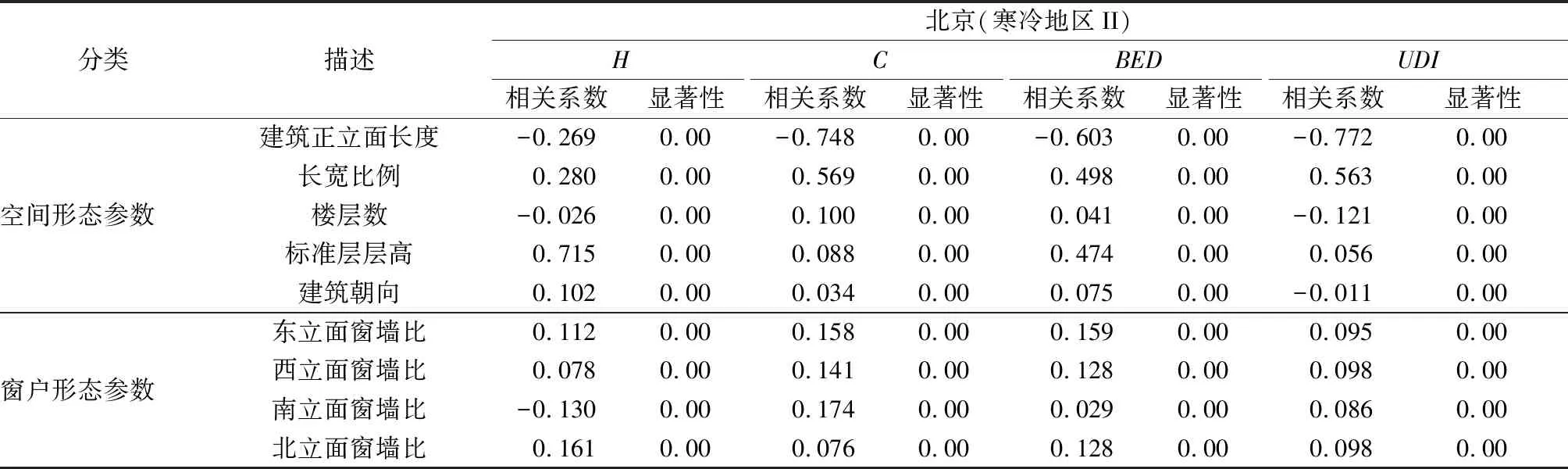
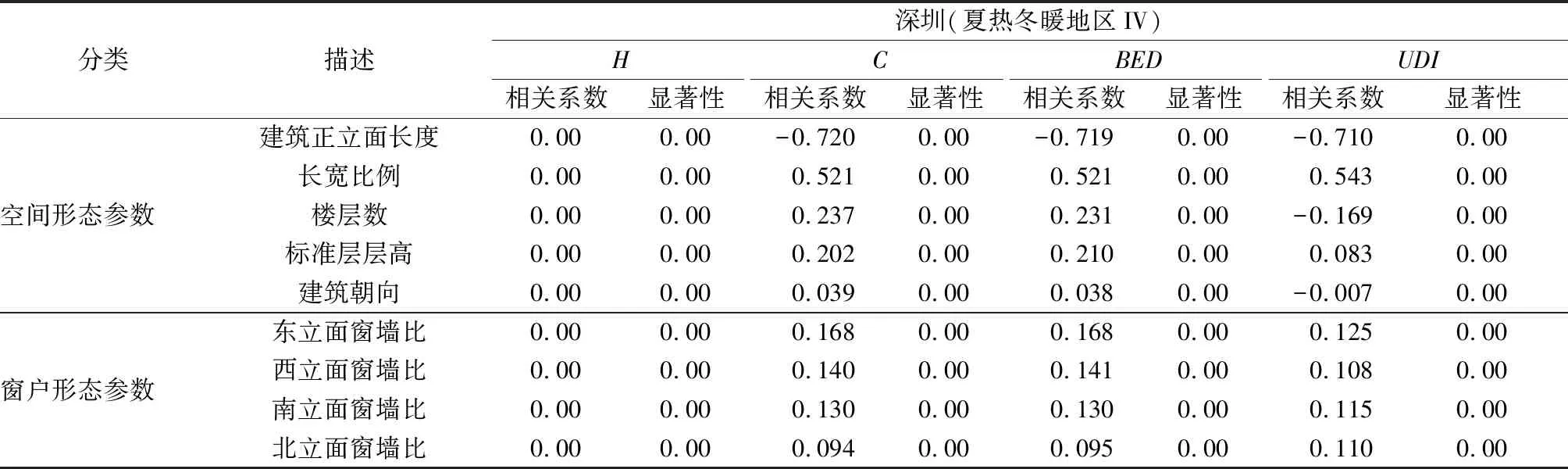
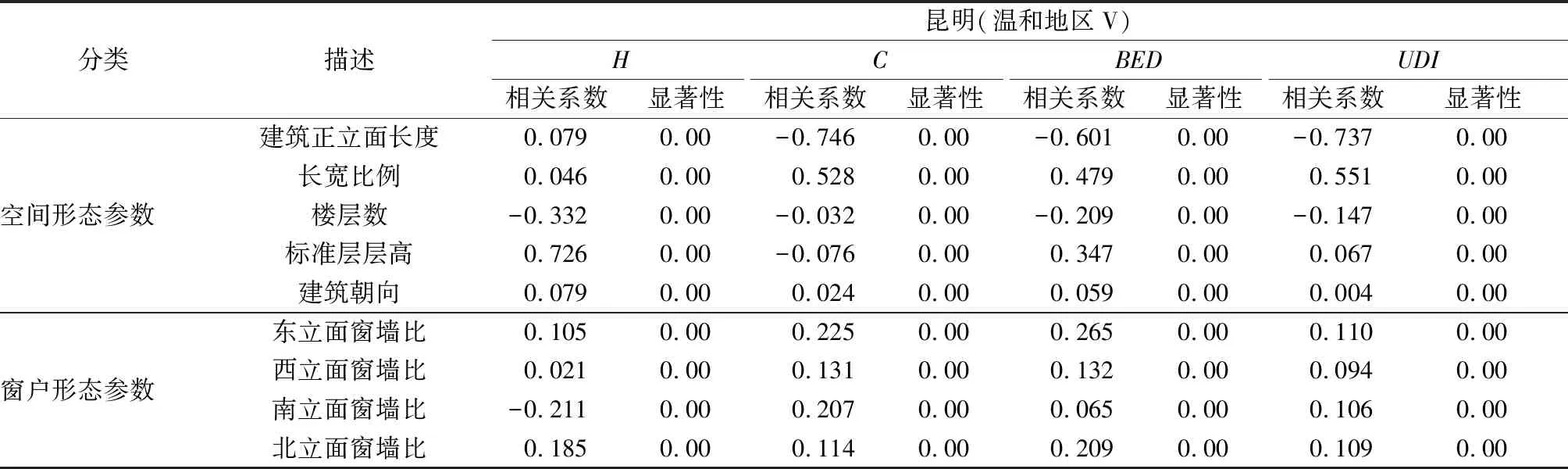
3.2 建筑形态参数与性能指标的相关性分析
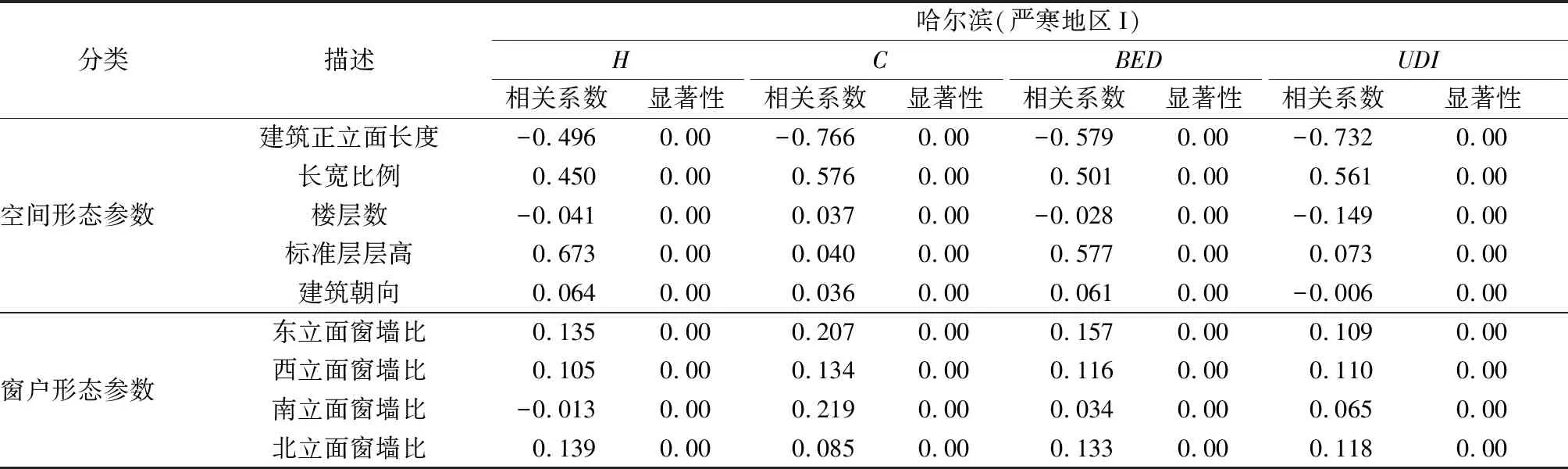
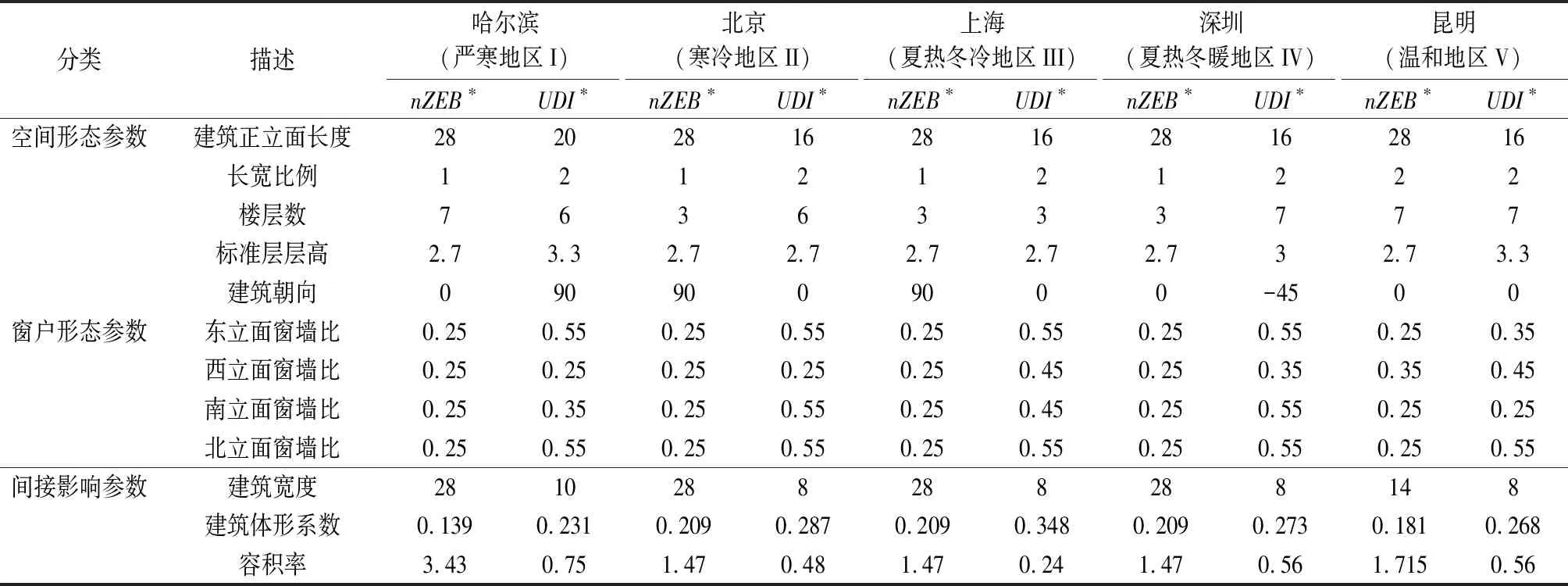
3.3 典型城市的住宅建筑形态优化设计结果


4 结束语

