大型设备吊装换填地基承载特性的数值分析*

郭 忠 宋二祥 林世杰 刘光磊 徐钰棋 付 浩 童希明 焦公琦

(1.中石化重型起重运输工程有限公司， 北京 100029； 2.清华大学土木工程系， 北京 100084；3.北京中岩大地科技股份有限公司， 北京 100041)

0 引 言

在石油、化工、冶金等行业的工程建设中，一般总有大型设备的吊装问题(图1)，比如分离塔、精馏塔、汽提塔等。这些设备往往高达数十至上百米、重达数百乃至上万牛顿，一般采用大型履带式起重机进行吊装，依据吊装设备的情况，须选用不同起吊力的吊车，吊车与设备往往重达到数万牛顿。这样大的荷载，显然需要对吊车站位区域的地基进行处理才能满足吊装过程中对地基承载力和差异沉降控制的要求。

对于强度不能满足的地基，目前一般采用换土垫层法对地基进行处理，再在处理后的地基地面铺设两排路基箱，吊车的两履带各压在一排路基箱上。两排路基箱相当于两个矩形“基础”，吊车及设备的重力通过两条履带传给这两个“基础”，再经这“基础”传给地基，亦即垫层和下卧层。

对建筑基础下的换土垫层地基，业内已有较多的工程经验，并有相应的技术标准可循[1]。而吊装工程中的上述地基基础体系显然不同于任何建筑地基，相关研究尽管已引起业内科技人员的重视[2]，但总体来看研究还较少，故现行GB/T 51384—2019《石油化工大型设备吊装现场地基处理技术标准》[3]基本采用JGJ 79—2012《建筑地基处理技术规范》[1]中的设计验算方法。对此业内不少专家深感疑虑。吊装地基基础的变形及荷载传递特性如何，其承载力验算到底应采用怎样的方法，是业内急需研究的问题。

为此，结合一实际吊装地基处理项目，通过有限元模拟及实测分析研究此类地基基础的承载特性。首先通过计算和实测分析，揭示此类地基基础体系在工作荷载下的变形及荷载传递特性，并检验所构建弹塑性有限元模型的合理可行性。进而通过有限元计算研究此地基基础体系的承载力安全系数，并与JGJ 79—2012建议简化方法的验算结果比较。还对履带下所压路基箱是否连接、承载力计算时是否可取单侧路基箱按单基础计算、是否可用二维模型计算等问题进行比较讨论。所得认识可为发展简化验算方法提供参考。

1 吊装项目及地基处理概况

拟分析地基处理的吊装项目为中石化广西华谊75万t/a丙烯及下游深加工一体化项目，使用徐工集团XGC88000型4 000 t履带式起重机作为主吊车，主吊车重达20 090 kN，所吊装的丙烯丙烷分离塔(含吊具，见图1)重为19 600 kN，实测超起配重为14 700 kN，合计54 390 kN。

项目场地位于广西钦州港石化园区内，据勘察报告该场地原属海漫滩地貌，经填海整平后，场地自上而下依次为：①素填土；③淤泥质粉砂；④淤泥质黏土；⑤粉质黏土；⑥强风化岩(粉砂质泥岩、泥质粉砂岩、粉砂岩)；⑦中风化岩。其中素填土主要由黏性土、砂土及块状泥岩、泥质粉砂岩等组成，局部以砂土为主，土质松散不均匀，渗透系数较大，重型圆锥动力触探试验实测击数平均值为5.6击。地基各地层参数见表1。地下水位在地表下约2 m。

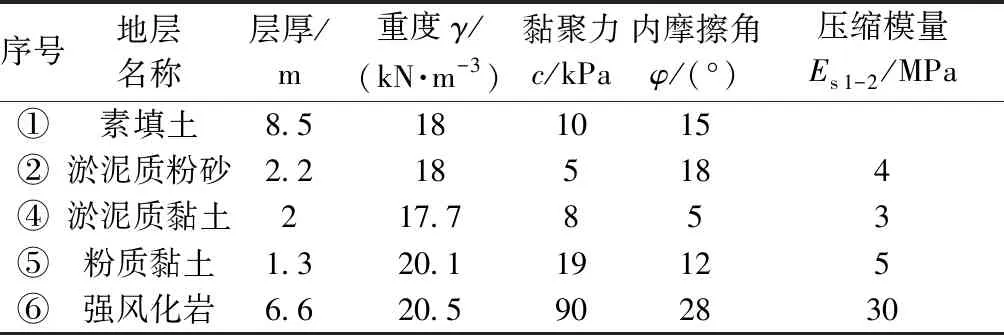
表1 地层参数Table 1 Parameters of soils

按此场地现状，不能满足吊装过程中吊车站位区域地基承载力及吊车倾斜度小于0.5%的要求，因此须采用换土垫层法进行地基处理。换土范围南北向长为35 m，东西向宽为24 m，换土垫层厚度为2 m。具体步骤为：挖除浅层一定深度的素填土，夯实基槽，再分层填筑从老旧建筑拆除的混凝土块体，每层填筑厚度约300 mm，并使用20 t振动压路机压实，垫层顶部100 mm铺设压实并整平的碎石、石粉混合物。

地基处理完成后，在垫层顶面铺设4 000 t级吊车专用路基箱，规格为8.00 m×2.80 m×0.27 m，每块重达137.2 kN，吊车两履带下各铺设一排10块，实际能同时压到7块，两排路基箱净间距为6.4 m。最大总荷载作用下，路基箱平均对地压力为183 kN/m2。铺设路基箱后的地基平、剖面图见图2。

地基处理过程中，在垫层顶面和底面布设压力和沉降监测传感器(土压力盒与静力水准仪)，两层传感器分别位于地表以下约0.26，1.93 m处，测得吊装过程中一些点位的竖向压力与沉降。吊装过程平稳顺利，两履带部位沉降差异不大，地基承载力完全没有问题。

2 地基基础体系的有限元模型

根据拟分析地基基础问题的特点，建立了三维弹塑性有限元模型，采用大型岩土有限元软件PLAXIS 3D进行计算分析。以下逐一介绍模型的各个方面。

2.1 路基箱的等效实心板模型

路基箱为一种板状箱形钢结构，由上、下盖板，侧板，内部筋板和侧面加强筋等构件焊接而成，并有吊耳便于吊运搬运。在采用有限元法模拟分析时，可按实际构造用多块板单元来模拟。但为在繁杂的计算分析中简化建模过程，本着截面抗弯刚度EI与抗剪刚度GA等效的原则给出路基箱的等效实心板模型。当固定泊松比取值的情况下，GA等效等同于EA等效。这样由EI、EA等效可计算确定等效实心板的模量Ee和厚度de，之后再由路基箱质量和等效实心板厚de确定等效实心板的重度γe。由此得到路基箱的等效实心板厚度和材料模量计算式：

(1a)

(1b)

式中：I为路基箱沿长度方向弯曲时的截面惯性矩；A为路基箱横截面钢板的截面积；B为路基箱宽度；Es为钢材的弹性模量。

路基箱规格为8.00 m×2.80 m×0.27 m，盖板和侧板厚30 mm，内部筋板厚20 mm，宽度方向分布有5块筋板，由此得出，A=2.016×105mm2，I=2.555×109mm4，所用钢材的弹性模量为206 GPa, 由式(1)计算得出：de=390 mm，Ee=38.0 GPa，进而计算给出γe=15.7 kN/m3。

2.2 土的本构模型及参数取值

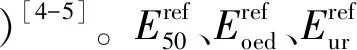
由于吊装属于快速加载，对水位以下的饱和黏性土按不排水计算，其强度采用由所给的固结不排水强度指标c、φ计算的不固结不排水强度，如式(2)[6-7]所示：

cu=c0+cincz

(2)

式中：c0为土层顶面的黏聚力；z为从地面起算的深度；cinc为黏聚力的深度增长率。

对于渗透性较好的土层则按排水计算。

各土体的材料参数取值见表2，其中各模量值考虑地勘报告所提供值一般均偏低较多，根据计算沉降与实测比较进行粗略反分析后进行了调整，而强度指标仅考虑换土施工过程中对槽底压实而对此深度以下3 m内的素填土参数进行了调整(表2的密实素填土)，其余均按地勘报告，以如实计算地基承载力的安全系数。

2.3 地基基础的整体有限元模型

整体有限元模型平面尺寸为80 m×80 m，深20.6 m，原地基土体近似按水平分层，以强风化岩下的中风化岩顶面作为模型底部固定边界。

采用线弹性实体元模拟路基箱和吊车，前者采用2.1节所述参数，铺设缝隙为70 mm(因吊钩在路基箱侧面)；后者则是将吊车底座车架与履带合为一个整体，按外形粗略建模，由于履带架的抗弯刚度比路基箱大很多，这里弹性模量取100 GPa，泊松比0.3，重度取零。吊车重力、吊装设备重力以及为减小偏心所施加的配重作为一个总集中力据其偏心情况施加在吊车模型的相应部位。可以看出：模型能方便地考虑荷载可能的偏心。但此项目中所用吊车可较为准确地调整配重及其力臂，使偏心距很小，故计算中认为偏心距近似为零，将总荷载以竖向集中力形式施加于吊车模型的形心位置(图3)。

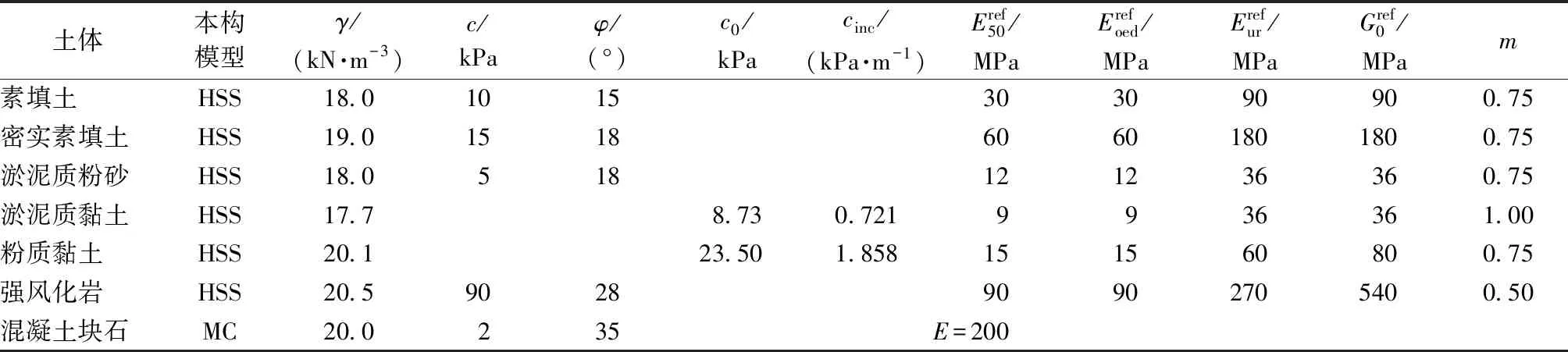
表2 土体模型参数Table 2 Soil model parameters

3 吊装荷载下的计算及实测对比

计算分地基处理、路基箱铺设、吊装三个步骤，吊装过程中设备与起重机总重53 900 kN，故在吊装工况下施加集中荷载F0为54 390 kN。

吊装荷载作用下，吊车与路基箱发生了整体下沉，地面沉降云如图4所示。最大沉降为60 mm，发生在履带后端，两条履带沉降分布基本一致。整个路基箱长度方向两端差异沉降为13 mm，而履带前、后两端沉降相差10 mm，由此引起吊车的倾斜度为0.6‰，远低于5‰的安全限值。

选取沿基础长度方向的1—1剖面和基础宽度(单块路基箱长度)方向的2—2剖面(图2a)，对比吊装荷载作用下的竖向压力和沉降的计算值与实际监测值，分别如图5、图6所示。底层沉降监测传感器损坏较多，有效数据较少。这里X、Y坐标的原点均对应于吊车平面的形心(图2a)。

计算竖向压力与实测值的对比如图5所示。计算结果沿履带长度方向看，基底压力呈两端较大、中部较小的抛物线形，表现出刚性基础的特性；而在基础宽度(单块路基箱长度)方向，基底压力近似均匀分布，表明路基箱的刚度不是很小。

实际监测结果中，由于路基箱表面不平整、回填块石局部架空等原因，竖向压力分布很不均匀。基底压力分布情况与计算值相差较大，1—1剖面中段和2—2剖面路基箱位置的中部对应于履带正下方，该处的竖向压力远高于平均对地压力，表明相对块石垫层来说路基箱的刚度还不算很大。同时，在路基箱平面范围外的垫层底部竖向压力明显大于该处的自重应力，表明附加压力经垫层后有一定扩散。

计算沉降与实测沉降沿1—1、2—2剖面的对比示于图6，可见总体趋势较为吻合。计算显示1—1剖面沿履带长度的沉降分布基本为直线，表明履带架的很大刚度。但在垂直履带长度方向的2—2剖面沉降显示，路基箱受压后实际弯曲程度高于计算值，实测路基箱中部受压处与边缘的差异沉降大于30 mm，而计算不到15 mm。其原因应是对块石垫层采用连续介质力学模型计算沉降分布有较大误差。

考察沿南北方向1—1剖面的沉降分布，计算和实测都显示南侧的沉降较北侧大一些。开始推测是吊车位置相对于垫层平面偏南所致，但将吊车连同路基箱整体北移，使吊车平面中心与垫层形心接近，计算仍给出南侧的沉降较大。进而注意到吊车的每条履带相对其下一排7块路基箱并不完全对称，履带最北端所压的一块路基箱外伸较多些(图2)。为此，保持路基箱位置不变，仅将吊车相对其下路基箱稍向北移，使每条履带均位于其下一排7块路基箱的正中，则计算给出的南、北沉降几乎无差异。这表明，实际吊装中尽量使吊车相对于其下所压路基箱无偏心，对减小差异沉降有较重要的作用。

上述计算与实测对比总体上较为吻合，但也有部分测点有较明显的差异，其主要原因应是对于块石垫层的实测及连续介质力学模拟均有较大难度。

从实测与计算分析可清楚看出该地基基础体系的变形特征：最大沉降总是发生在履带部位，沿履带长度的沉降基本为直线，而履带部位与履带以外部位的路基箱会有较明显的差异沉降，而路基箱部位与路基箱范围以外的周边地面又有较大的差异沉降。总体沉降和差异沉降大小可反映该地基基础体系的强弱。但在承载力足够时，主要须控制两履带之间和各履带前、后部位的差异沉降。在地基较为均匀的情况下，为控制履带部位的沉降差，关键是要控制荷载的偏心距。这里结合实测分析的一个发现是，履带相对所压一排路基箱在前、后两端是否对称，对控制履带前、后的差异沉降有着不可忽略的影响。

4 地基承载力及几个影响因素分析

换填地基的承载力验算是一较复杂的问题，JGJ 79—2012中建议的方法是一种经验性的简化方法。首先对于垫层，由于只是在基础附近一定范围内存在，不能像较大范围内存在的持力层那样计算其承载力，而只能根据经验粗略估计。对于下卧原地基的软土层，则考虑基底附加应力经垫层按一定扩散角扩散到下卧层，进而得出下卧层所受总压力，再按容许承载力法验算下卧层的承载力。这种方法很近似，且一般偏于保守，特别是将JGJ 79—2012方法直接用于临时性吊装地基时更是如此。

由于研究很少，现行GB/T 51384—2019对换填地基设计基本采用JGJ 79—2012的设计方法，但对下卧层承载力的计算既考虑深度修正也考虑宽度修正。而在行业工程实践中，下卧层承载力的验算又超出GB/T 51384—2019的规定，比如对一般换填厚度多取扩散角为30°，大于JGJ 79—2012建议值；基础宽度就取单块路基箱的长度，这往往也大于JGJ 79—2012规定的取值。但这里垫层超出路基箱较少，扩散角最大取22°，因此，计算得到的地基下卧层顶面压力为178.0 kPa。按《工程地质手册》[8]公式计算给出条形基础情况下的下卧层极限承载力为338.5 kPa，再考虑基础形状修正，认为安全系数不小于2，满足要求。但严格按GB/T 51384—2019验算并不满足。

因此，采用有限元法计算该吊装地基的极限承载力，进而估计其安全系数。并对垫层强度的影响、路基箱是否连接对此地基基础体系承载性能的影响，以及按二维与实际三维计算、按单基础与实际双基础计算的差异等进行了计算讨论，为此类地基基础问题承载力验算方法的改进提供依据。

4.1 实际地基基础的极限承载力计算

在上述计算的基础上，继续增大荷载直到地基破坏，计算给出的荷载-位移曲线如图7所示。随着荷载增大，曲线趋于水平，给出极限荷载为实际荷载的2.9倍，亦即理论上安全系数可达到2.9。从工程稳妥角度保守取值安全系数也可达到2.5。

显然，如上建模计算完整考虑了垫层本身力学性质对地基基础体系承载力的影响。如果垫层的强度提高则整个体系的承载力也会有所提高，这是上述技术标准所建议简化方法所不能考虑的。为展示这一点，将块石垫层的抗剪强度指标改为c=2 kPa，φ=40°，剪胀角改为ψ=10°，其余参数不变，则按荷载计算的安全系数由2.9增大为3.1(图7)，而实际吊装荷载下地面最大沉降由60 mm减小为56 mm。

过吊车平面中心点取横竖两个剖面显示破坏时的位移增量场如图8所示，可以明显看出场地中部下沉，四周隆起。

此外，在吊装项目中，吊车质量、所吊设备质量以及配重块的质量均是可事先较准确估计的，离散性较大的是地基土层的强度指标，故采用降低强度指标的方法计算该地基基础体系按第二定义的安全系数，亦即土体所具有的强度与保持土工结构恰好稳定所需要的土体强度之比[4]。图9给出强度指标降低倍数-沉降位移关系曲线，可见按第二定义的地基承载力安全系数为1.8。由此可知，对该问题采用第二定义安全系数时，要求安全系数达到的值可以小一些。

4.2 路基箱刚度及其连接与否对承载性能的影响

4.2.1路基箱刚度对地基承载性能的影响

按塑性力学理论，地基承载力极限值与基础刚度无关，但是加大基础刚度显然会减小正常荷载下的沉降差。当上部结构对差异沉降敏感时，会提高地基的容许承载力。

对于这里分析的地基基础问题，如将路基箱的刚度提高1倍，计算给出的极限承载力没有变化。但在实际吊装荷载作用下，地基差异沉降减小(地面沉降云与图4类似)，主要是沿路基箱长度方向的差异沉降因路基箱刚度增大而减小，比如沿2—2剖面部位的路基箱，履带下方与路基箱端头部位的差异沉降由12 mm减小到8 mm，但整个地基的最大沉降仅稍有减小，从60 mm减小到58 mm。履带前、后两端差异沉降仍为10 mm，与原模型相等，这是因为履带架有很大的刚度，而荷载分布、履带相对于路基箱的位置没有变化。

如前所述，对吊装地基，须控制的是两履带间及其前、后的差异沉降，也就是说履带与履带所占范围之外的差异沉降不需要很严格的控制。由此看来，目前路基箱的刚度是合适的，不必再行增大。

4.2.2路基箱连接与否对地基承载力的影响

前已述及，基础刚度大小对地基的极限承载力无影响。但在吊装工程中，履带下铺设的一排路基箱之间不但没有任何连接，还因吊钩设于路基箱侧边往往会有数厘米的缝隙，这缝隙显然不能调整路基箱之间的荷载分担。

由地基基础的承载力理论可知：对于较大刚度的基础，当其所受荷载逐步增大时，基底边缘部位的土首先进入塑性阶段，之后基底压力因边缘部位土体变弱而向基底中部土转移，从而使地基可以承受更大的荷载，直至地基承载力完全发挥。这里基底压力分布随荷载增大而发生的变化，显然有赖于基础自身的刚度。如基础没有刚度，基底压力分布只能是与基础所受荷载分布保持一致，从而地基承载力不能充分发挥，亦即极限承载力将减小。

但在所分析的地基基础问题中，相互分离的路基箱是由刚度很大的履带架施加荷载。对于这样的一个地基基础体系，路基箱是否连接对体系承载性能到底有无影响，显然是个需要研究的问题。为此，这里将每条履带压到的7块路基箱连接成整体，其他参数不变，通过计算对比来回答这一问题。

计算给出实际吊装荷载下的地面沉降云与图4类似，其最大沉降、差异沉降与原模型基本相同，最大沉降仍为60 mm。继续加大荷载进行计算直到地基破坏，得到地基极限承载力也无变化，安全系数仍为2.9。也就是说，路基箱是否连接对此地基基础体系的承载性能基本无影响。

仔细考察计算结果可知，原模型中尽管路基箱是分散的，但由于刚度很大的履带架经履带压在一排路基箱上，使所压一排路基箱在很大程度上已经形成一个整体。可以理解为即使将履带所压的几块路基箱在接缝处刚性连接，路基箱内的荷载传递仍然主要是从履带向其左、右两侧沿该部位路基箱的长度方向传递。因履带所依附的履带架刚度很大，所压路基箱不管是否相互连接，它们在履带处的沉降基本相同，这就决定了从履带往两侧沿路基箱长度不同部位的沉降及箱底压力也都基本相同(图10)，这样相邻路基箱在接缝处连接与否便没有区别。

当然，如果将履带前、后两端处原本不受压的路基箱也连起来，就等于加大基础面积，自然会提高地基基础的极限承载力。例如，在每条履带压到的7块路基箱前、后各增加1块，将这9块路基箱联成整体，材料参数不变。在吊装荷载作用下，地面沉降云如图11所示。结果显示，实际吊装荷载作用下，路基箱对地压力减小，整体沉降也有所减小，地面最大沉降为49 mm，发生在基础中部，履带前、后两端差异沉降大幅减小为2 mm。承载力安全系数则提高到3.6，安全系数提高的幅度略低于基础面积扩大的幅度。

当然，这种加长不能过多。一是垫层范围不宜太大，二是加长到一定限度后，远端路基箱的作用非常小，不经济。

4.3 二维模型与三维模型的差异

若将路基箱近似看成条形基础，则可采用平面应变模型计算。地基土体、回填块石、路基箱和吊车的材料参数与三维模型相同，在吊车中心施加集中荷载，实际为线荷载，建立二维有限元模型如图12所示。

吊装荷载对应的线荷载由F0除以7块路基箱构成基础的长度20.02 m得到，为2 717 kN/m。

计算得到承载力安全系数仅为1.65，远低于三维模型的计算结果。由JGJ 79—2012建议的简化验算方法也可以理解，条形基础时为单向扩散，矩形基础时为两向扩散，所以两种模型的计算结果差异明显。

4.4 仅取单侧路基箱及相应垫层的承载力计算

上述按实际情况进行两排路基箱经履带吊加载的计算，相当于双基础下地基承载力的计算。但按GB/T 51384—2019方法验算时一般是取一侧履带及其下路基箱进行验算。为比较单双基础的差异，这里建立单基础模型进行计算，模型中仅保留一排路基箱，同时将地基处理范围缩小一半，施加单条履带荷载(图13)。

图14为荷载倍数-位移曲线，给出安全系数为2.7，较按实际情况的计算值2.9小7%。这里实际情况中的两排路基箱，类似双基础，具有一定有利作用，但这里基础间距与宽度比为(8+6.4)/8 =1.8，已相对较大，双基础的有利作用不大。

由上可以理解，采用GB 51384—2019所建议的简化验算方法对此类地基的承载力进行验算时，取单排路基箱是合理的。

5 结束语

结合中石化广西华谊大型设备吊装项目，对吊装地基结合现场实测进行有限元模拟分析，揭示此种地基基础体系在实际荷载作用的变形与荷载传递特性，还对其极限承载特性及有关影响因素进行了深度研究，主要结论有以下几点：

1)在吊装荷载作用下，此种地基基础体系的最大沉降总是发生在履带所处部位，从履带到其范围之外的路基箱再到路基箱范围之外的地面沉降依次减小。沿履带长度的沉降分布因履带架的很大刚度基本是直线分布。如地基较均匀，荷载偏心小，则履带前、后及两履带间的沉降差很小，完全满足差异沉降小于0.5%的要求。实测分析还表明，履带前、后相对所压一排路基箱是否对称，对履带前、后的沉降差有着较显著的影响。

2)由于整个荷载是通过履带压到刚度并非很大的路基箱再传给垫层、下卧层，在实际吊装荷载下，下卧层顶面附加应力并未看到GB/T 51384—2019中设想的按一定扩散角扩大面积上的近似均匀分布，而是在履带下方的压力明显较大。但在路基箱对应范围以外的下卧层顶面压力明显大于该处的竖向自重应力，表明附加应力经垫层还是有一定扩散的。

3)尽管该换填地基的承载力按GB/T 51384—2019建议的方法进行验算并非完全满足，但现场实施结果以及三维弹塑性有限元计算均表明，按极限荷载计算的地基承载力安全系数可达2.9，这说明JGJ 79—2012建议方法对此种地基基础体系的验算偏于保守。

4)结合实测的计算分析表明，对吊车履带所压一排路基箱是否连接为一整体对此地基基础体系的承载性能无明显影响，但如在两端各增加一块路基箱并与履带所压路基箱刚性连接，则可显著提高地基承载力并减小沉降。

5)该地基基础体系本质上属于双矩形基础，有限元计算对比表明，如取一侧路基箱按单基础计算则承载力安全系数略有减小，但如按条形基础用二维有限元模型计算则给出明显偏小的安全系数。这意味着简化验算时取一侧路基箱按矩形基础进行承载力验算的做法是合理的。

相信以上认识对进一步研究构建针对此种地基基础体系的简化验算方法有着重要参考价值。