基于DDPG深度强化学习的电站脱硝过程优化控制

林康威，肖 红，姜文超，杨建仁，熊广思，黄冠儒

(1.广东工业大学 计算机学院，广州 510006；2.广州云硕科技发展有限公司，广州 511458)

0 引言

近年来，随着新能源产业迅速发展，我国能源结构不断发生调整，煤在能源消耗中所占的份额有所减少，但预计在未来很长的一段时间内，燃煤发电产业仍占据着主导地位[1]。燃煤发电会产生污染有害气体，其中含有SO2、NO、NO2等。因此，目前在火力发电厂实现控制NOX排放含量，常采用的成熟技术手段有SCR(选择性催化还原法)和采用传统的PID控制来实现喷氨以达到脱硝优化的目的[2-4]。而实现精准建立SCR脱硝过程参数与SCR脱硝出口NOX排放浓度之间的映射关系是优化脱硝控制系统的关键基础。随着近年来人工智能算法技术的成熟，在现有的电站SCR脱硝系统出口NOX排放浓度的预测研究中，大多学者分别从机理建模与数据驱动的方法进行探究。其中，姚楚等[5]通过SCR脱硝系统的化学反应机理建立SCR动态预测模型，最终实验结果表明机理建模实现对脱硝系统的喷氨量控制效果优于传统的PID控制器的方法。但是，通过机理建模的方式，需要以研究对象为核心，根据化学反应建立数学守恒关系式，而燃煤电厂脱硝过程是一个复杂、非线性和多变量耦合的系统，导致机理建模很难精准描述。而相对于机理建模的方法，通过数据驱动建模的方式，不需要深入研究对象机理反应过程，只需以数据为驱动，通过建立人工智能算法构建预测模型。铉佳欢等[6]利用BP神经网模型应用在SCR脱硝系统中，实现预测SCR脱硝出口NOX浓度，从而使喷氨量得到精准控制，与传统PID控制器方式相比，BP神经网络能够很好对脱硝系统进行有效地控制，但是其模型的泛化性有待提高。温鑫等[7]通过构建深度双向LSTM神经网络模型，实现电站SCR脱硝系统的出口NOX排放预测，实验结果显示与传统的BP神经网络模型相比较，误差精度下降了约5%，但是双向LSTM神经网络模型结构复杂，且模型需要优化的超参数较多。丁续达等[8]基于最小二乘支持向量机LSSVM模型，实现SCR脱硝系统在线NOX预测，但是模型的预测精度和泛型性上还未能达到实际工业生产的需求。虽然上述的方法不依赖于过程的结构与机理，适合非线性强，过程复杂的预测对象，但针对火力发电站SCR系统中普遍存在着多参数耦合、调负荷、多工况等情形，单一模型的预测精度很难达到实际应用于工业领域生产的需求。因此，针对电站脱硝系统在多参数、多变工况条件下NOX排放预测精度较低的问题，提出基于MiniBatchKMeans聚类与Stacking模型融合的SCR脱硝过程NOX预测方法。首先对SCR脱硝系统的各运行工况进行聚类分析，然后在聚类划分基础上，在多工况样本集以及在同工况样本集上，利用Stacking-XRLL多模型融合预测模型对电站脱硝系统出口NOX浓度进行预测。实验研究结果显示，该模型在多工况下预测精度远优于BP、LSTM、GRU神经网络模型，平均精度达到99%。

另外，实现脱硝系统出口氮氧化物超低排放是电站优化控制的重要手段。由于燃煤电厂脱硝过程的NOX排放受机组负荷、喷氨质量流量、SCR入口烟气O2量、SCR入口烟气温度等运行参数影响。因此，要实现SCR脱硝系统的NOX超低排放控制，首先需构建SCR脱硝系统可控运行参数与SCR出口NOX排放的映射关系模型[9-11]，然后再建立含有约束条件的目标优化函数，最后基于遗传或粒子群优化算法对目标函数进行寻优[12-15]，在满足国家要求NOX排放浓度低于50 mg·m-3约束条件下，以获取SCR脱硝过程各可控运行参数的最优值。但是，采用传统遗传和PSO优化算法存在收敛性不足以及局部最优解。符基高等[16]基于LSTM时间循环神经模型结合深度强化学习A3C算法，实现燃煤电厂SCR脱硝效率的控制策略。但是LSTM神经网络模型与A3C深度强化学习算法相结合之后，存在模型训练速度慢，且优化得到的是局部最优解，并且评价策略通常不是非常高效，并且有很高的偏差。因此，在同时兼顾考虑烟气NOX超低排放与脱硝效率之间的关系，基于MiniBatchKMeans聚类与Stacking模型融合的SCR脱硝过程建模方法，并利用深度确定性策略梯度DDPG算法对参数寻优，为实现现场实时优化控制奠定重要的理论基础。

1 基于MiniBatchKMeans聚类与Stacking的多模型融合算法设计

1.1 算法理论介绍

1.1.1 MiniBatchKMeans聚类算法

MiniBatchKMeans算法是K-Means算法的变种，采用随机产生的小批量数据子集进行聚类，大大减少了计算时间，因此当运用在大数据集样本上时，MiniBatchKMeans能够保持聚类准确性并可以大幅度降低计算时间。

MiniBatchKMeans算法流程伪代码如下：

function MiniBatchKMeans(输入数据，中心点个数K){

获取输入数据的维度D和个数N;

随机生成K个D维的初始质心;

while(算法未收敛){

从原始集随机抽取N个样本构建小批量样本集;

对N个点：计算每个点属于哪一类;

对于K个数据中心点：

(1)找出所有属于自己这一类的所有数据点;

(2)将自己的坐标值修改为这些数据点的中心点坐标;

}

输出结果;

}

两个样本点a=(a1,a2,a3,…,an)和b=(b1,b2,b3,…,bn)之间距离计算如式(1)所示：

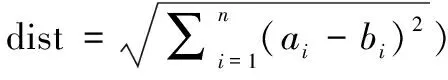
(1)

第i个类中心计算公式如式(2)：

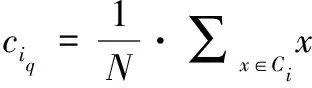
(2)

其中:ciq表示第i个类的类中心，Ni表示第i个类中的元素个数，Ci表示第i个类。

加入批量大小为batch的小批量样本集X={X1,X2,X3,…,Xbatch}后的类中心为ciq，计算方式如式(3)：

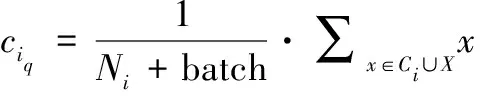
(3)

另外，使用误差的平方和作为度量聚类质量的目标函数func，定义如式(4)：

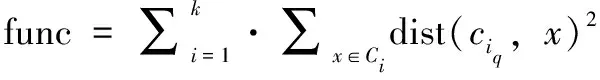
(4)

1.1.2 XGBoost算法

极端梯度提升(XGBoost, extreme gradient boosting)是Tianqi Chen在2016年提出的基于Boosting Tree模型的分布式学习框架，该模型的基础学习器为决策树。与传统的Boosting树模型不同的是，传统树模型只使用一阶导数信息，当训练n棵树时，由于使用前n-1棵树的残差，因此很难实现分布式训练，而XGBoost对损失函数进行了二阶泰勒展开，它可以自动使用CPU的多线程进行分布式计算。另外，在目标函数中引入正则项，以避免模型过拟合，提高泛化性。假设有一个数据集D，D={(xi,yi):i=1…n,xi∈Rm,yi∈R}，则可以得到n个观测值，每个观测值有m个特征以及相应的变量y。因此，广义模型定义如下：

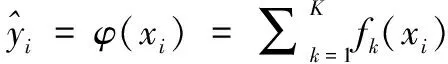
(5)

在式(5)中，fk表示的是一个回归树，fk(xi)表示第k棵树对数据中的第i个观察值给出的分数。为实现目标函数fk，应最小化以下正则项目标函数。

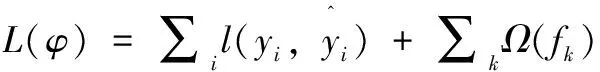
(6)

其中:l是损失函数，为防止模型过拟合，惩罚项中Ω应包括以下项：

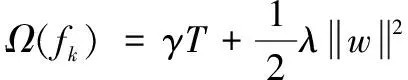
(7)

其中:γ和λ分别表示叶子数量T和叶子权重w的惩罚参数。Ω(fk)目的是为了防止模型过拟合而简化该算法生成的模型。

为使目标函数最小化，采用迭代法。在第j次迭代中添加fk，以最小化以下目标函数：

(8)

使用泰勒展开式来简化上述函数，并推导出从给定节点分割树后的损失函数：

(9)

其中:I是当前节点中可用观测值的子集，IL，IR是分割后左右节点中可用观测值的子集。函数gi和hi的定义如下：

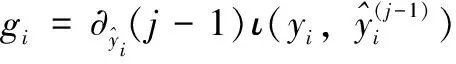
(10)

(11)

1.1.3 Light GBM算法

Light GBM算法是基于GBDT(gradient boosting decision tree,梯度提升决策树)模型提出的[17]。虽然GBDT在很多机器学习任务上都取得了较好的学习效果，但近年来随着数据量的增长，传统的GBDT算法在构建决策树时需要找到最优的分割点，一般的方法是对特征值进行排序，然后枚举所有可能的特征点。但是此种方法不仅在时间性能上表现较差，而且需要很大的内存。因此，GBDT算法面临着精度和效率性能的问题急需解决。

Light GBM算法使用了改进的直方图算法，它将连续的特征值划分为k个区间，在k个值中选择划分点。因此，Light GBM算法在训练速率和内存占用率上都优于传统的GBDT树模型。同时，决策树是一个弱分类器，使用直方图算法会有正则化效果，可以有效防止过拟合。在减少更多误差方面，Light GBM算法采用leaf-wise生成策略。另外，在减少特征数量方面，传统采用的方法是PCA，PCA一般用于特征冗余的情况下，因此有一定的局限性。Light GBM算法使用的EFB算法将高维数据的特征放在一个稀疏的特征空间中，以避免计算冗余特征，并根据算法构造直方图，可以加快计算的速度。综合所述，Light GBM算法在不降低预测准确率的同时，加快预测速度，并降低内存占用。

1.1.4 线性回归算法

线性回归分析是机器学习中的一种统计方法，可分为简单线性回归和多元线性回归，用于估计一个或多个输入变量和输出变量之间的关系。线性回归用直线模拟输入变量x和输出变量y之间的关系。

一次方程定义如式(12)：

y=β0+β1x

(12)

其中:参数β0和β1是回归系数。而模型的拟合度衡量标准，即它对输出变量y的在n个数据点上εi的误差大小。

(13)

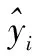
为评估回归模型的回归预测精度与真实值之间的误差，回归模型常用最小二乘法(LSM, the least square method，)估计进行拟合，找到误差平方和最小时的最佳拟合曲线或直线，即最小化。

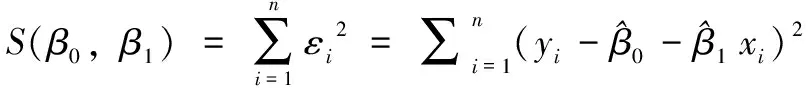
(14)

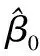
(15)

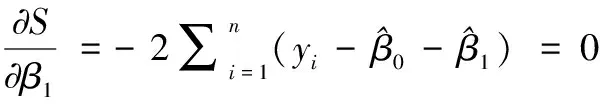
(16)

对上述两个方程进行化简，可以得到：

(17)

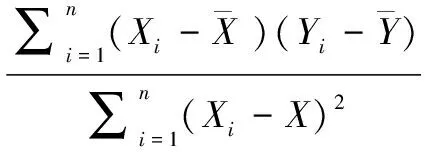
(18)

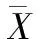
1.2 Stacking模型融合

Stacking是一种分层模型集成框架，在基于Stacking的集成学习模式下，通过融合多个机器学习算法的方式来提高整体模型的预测精度[18]。因此，在综合考虑Stacking模型融合算法的预测精度与训练性能，将Stacking模型融合框架划分为两层：第一层选择预测精度较高的XGBoost、RandomForest算法以及性能优异且时间复杂度较低的LightGBM算法模型作为基学习器；第二层，采用泛化性能力较强和稳健性较好的线性回归算法作为元学习器，如图1所示。

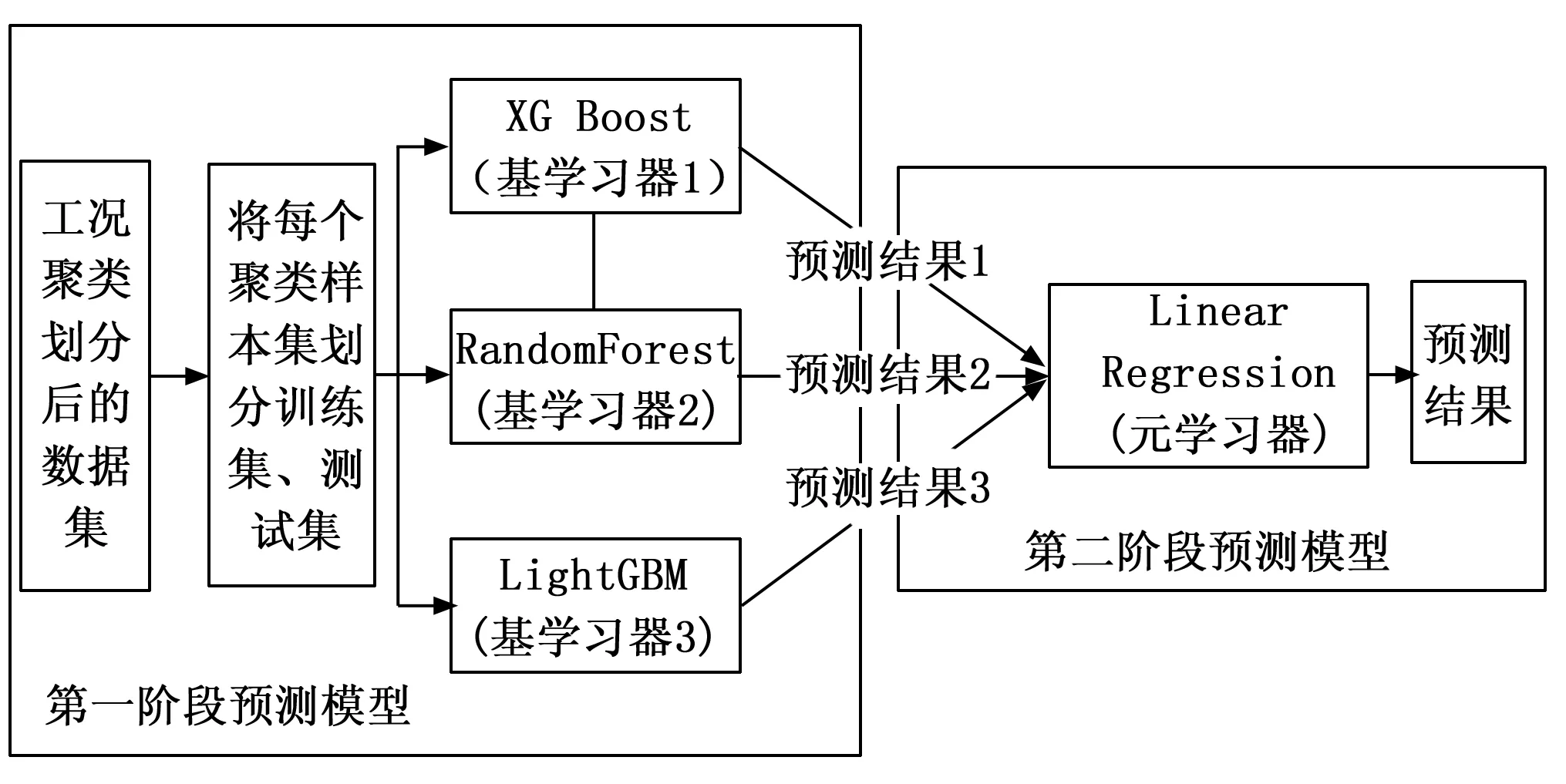
图1 Stacking模型融合架构图

针对电站锅炉脱硝系统在多变的工况环境条件下往往呈现出复杂的、大幅度滞后等特性，而单一模型在一定程度上很难准确地描述具有复杂的、非线性的火力发厂电站锅炉脱硝系统NOX排放问题，导致模型预测精度不高。因此，为了提高电站锅炉脱硝系统在多变的工况条件下NOX排放预测的精度，提出了一种基于MiniBatchKMeans聚类与Stacking多模型融合框架的电站脱硝过程建模方法，如图2所示，其建模步骤如下：1)将从DCS采集的数据集进行预处理，其中包括剔除异常值样本和筛选稳态工况，并按照一定比例(4:1)来划分训练集与测试集；2)利用MiniBatchKMeans算法对训练集参数进行工况聚类和划分，保存最优的轮廓系数和聚类中心，得到Ci个聚类样本；3)对这些聚类样本，利用如图1所示的融合方法，采用XGBoost、RandomForest、LightGBM机器学习算法作为Stacking模型融合框架的第一层(基学习器)，以线性回归作为第二层(元学习器)，构建嵌入多个机器学习模型的Stacking模型融合框架预测算法，用于处理多工况下NOX的预测问题。

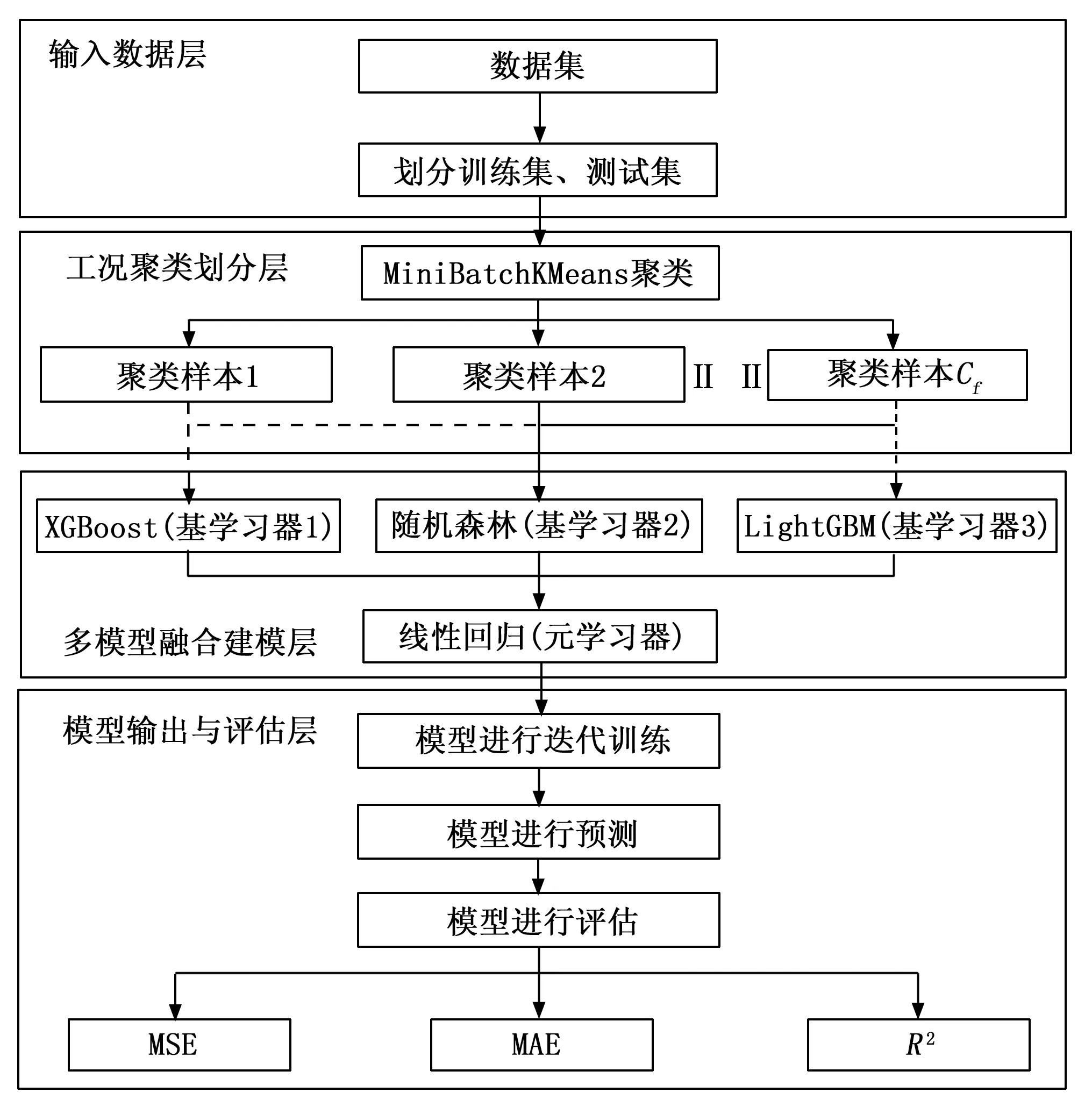
图2 基于MiniBatchKMeans与Stacking多模型融合框架的建模流程图

2 基于深度强化学习DDPG算法的脱硝效率控制策略模型

2.1 DDPG算法理论

2.1.1 基于Actor-Critic的深度策略梯度方法

Actor-Critic是由Actor和Critic两个神经网络构成。Actor负责针对Critic网络评价来纠正动作的偏向。Critic负责对Actor生成的动作进行评分。它们整个网络的工作流程大致如下：1)首先Actor依据当前的环境生成action;2)环境依据Action给与相应的回报r;3)Critic会对action进行评价;4)Actor会依据Critic的评价来调整策略，输出新的action;5)Critic会依据回报r来纠正评价规则。不断循环(1)～(5)，直至所有的网络收敛或达到设定训练周期的阈值。

在Actor-Critic网络中，通常情况下，Critic是一个状态值函数，在每次动作选择之后，Critic会评估新的状态以确定事件是否比预期的好还是坏，这个评价就是时间差分法(temporal difference,TD)，数学表达式如式(19)所示:

V(st)←V(st)+α[rt+1+γV(st+1)-V(st)]

(19)

其中:V是有评判者(Critic)实现的值函数。TD误差用来评估所选择动作，即在某状态下所采取的行动。如果TD误差是正的，表示未来应加强选择的倾向，而如果TD是负的，表明未来应减弱这种倾向。这种假设动作是由Gibbs Softmax方法产生的，如式(20)所示:

(20)

式中，p(s,a)是行为者(Actor)在时间t的可修改策略参数，表示在每个状态s时选择每个动作a的倾向。对上述的加强与减弱可通过调整p(s,a)来实现，如式(21)所示：

p(st,at)←p(st,at)+βδt

(21)

式中，β是一个正的步长参数，这是一个奖赏惩罚方法。无论TD误差δ是正还是负，都会对策略进行更改。当δ为正时，增加动作的概率，δ为负时，减少动作的概率。

2.1.2 基于DDPG深度确定策略梯度方法

DDPG算法一种强化学习框架，基于策略梯度与DQN算法，DDPG能够解决Actor-Critic在连续动作空间的问题。例如在Gym和TORCS领域中，DDPG可以直接使用原始状态来学习，并且在Atari领域比DQN使用更少的经验学习步骤[19]。

DDPG的核心是使用一种随机的方法来探索好的行为，但估计一个确定性的行为策略(如式(22)所示)。只需在状态空间上进行整合，使得学习策略变得更加容易，但它也有可能无法探索完整状态和动作空间的局限性，为克服这个局限性，在随机探索的加入一个噪声Nt。

at=μ(st|θμ)

(22)

at=μ(st|θμ)+Nt

(23)

DDPG中的Actor和Critic是由神经网络设计的。Actor网络根据确定性策略梯度规则进行更新，而Critic网络则根据TD误差中获得梯度进行更新，如式(24)所示：

θμμ≈Εμ[αQ(s,a|θQ)|s=st,a=μ(st)θμμ(s|θμ)|s=st]

(24)

式中，为得到期望值，需要Critic网络在行动方面的梯度(w,r,t)以及Actor网络(w,r,t)和其它参数。DDPG网络参数的更新规则，采用小批量(mini-batch)数据样本，通过最小化式(25)中的损失来更新Critic网络，Actor网络使用采样策略梯度更新，如式(26)所示:

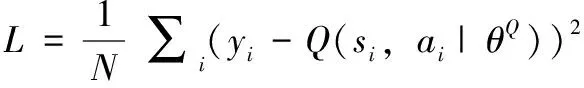
(25)

其中:yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)。

(26)

而目标Actor网络和Critic网络的参数更新如式(27)和(28)所示:

θQ′←τθQ+(1-τ)θQ′

(27)

θμ′←τθμ+(1-τ)θμ′

(28)

其中:τ是更新参数，将其设置为τQ1。

2.2 深度强化学习模型的建立

构建基于DDPG算法的SCR脱硝效率深度强化学习模型的整体框架如图3所示。在网络结构的设计中，Actor网络(主网络和目标网络)和Critic网络(主网络和目标网络)都包含两个隐藏层网络，每层神经元个数分别设置为256和128。Actor网络最后一层的激活函数为tanh函数，使得每一层的动作输出控制在[-1,1]之间，最终依据脱硝效率状态值限定范围得到脱硝系统各运行参数可控值。Critic网络对Actor网络得到的脱硝系统可控参数进行评估，采用relu激活函数。经过反复实验调试，DDPG模型的学习训练周期设置为500，Actor网络学习率设置为0.001，Critic网络学习率设置为0.002。

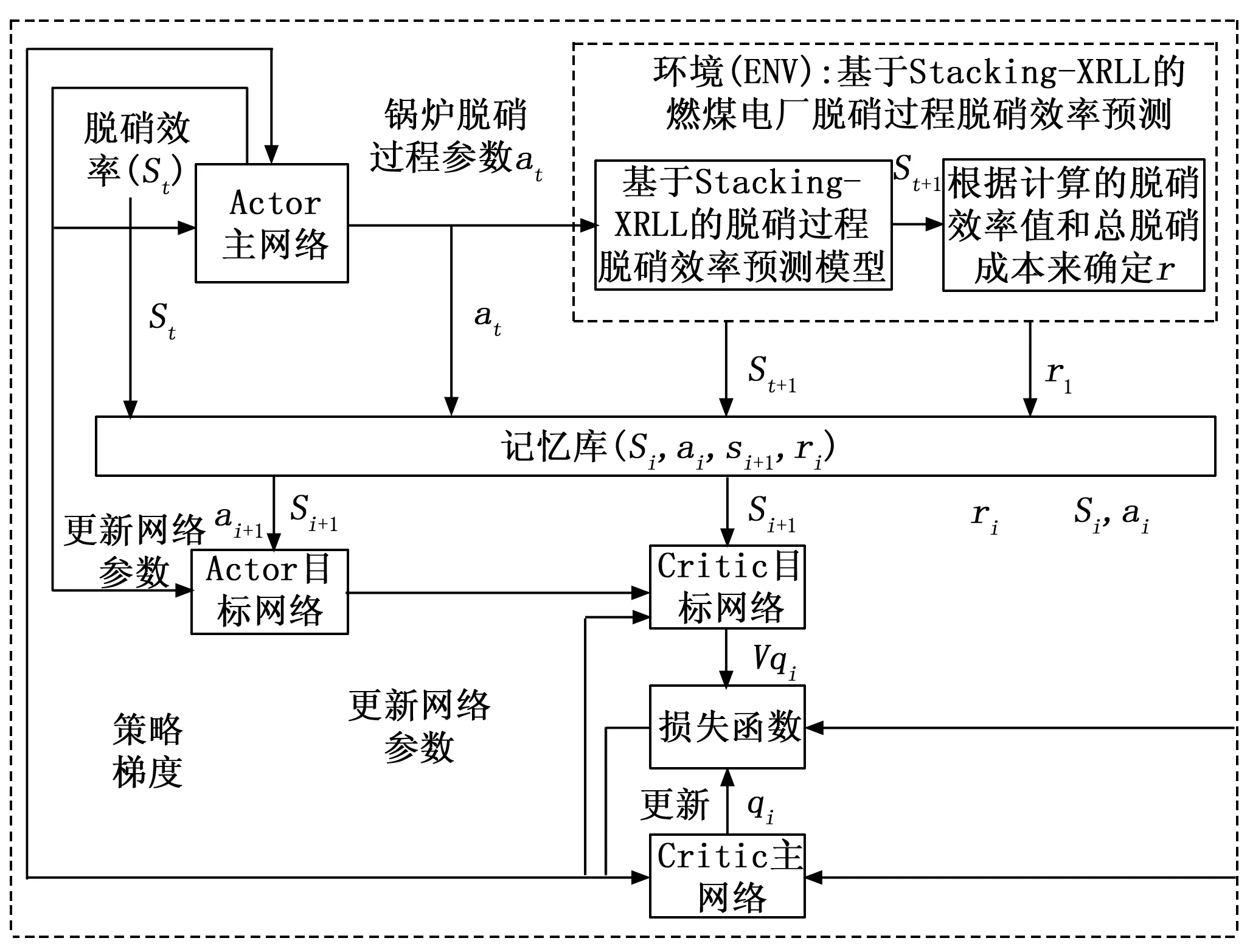
图3 基于深度强化学习DDPG模型的脱硝过程优化控制架构

DDPG算法模型选取机组负荷、喷氨质量流量、SCR入口烟气O2量、SCR入口烟气温度、SCR入口NOX质量浓度5个变量作为action动作值，脱硝效率(计算方式如式(29)所示)作为state状态值，且各参数变量取值范围设置如表1所示。

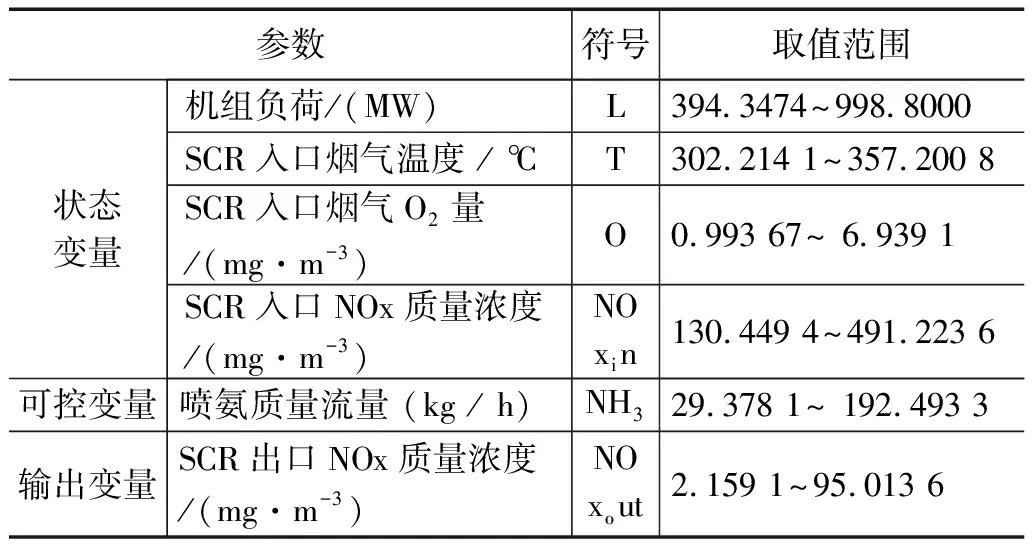
表1 电站锅炉各参数运行范围

(29)

式(29)中，η为脱硝效率，Inox＿in为SCR入口NOX质量浓度，Inox＿out为SCR出口NOX质量浓度。在SCR脱硝系统中，加大喷氨量，可以提高脱硝效率，但是过多的喷氨，另外会造成脱硝成本的提高。而喷氨量是衡量脱硝成本的重要指标，脱硝成本计算结果等于单位机组负荷下的喷氨量乘以相应单价。通常情况下，一般每台锅炉配备两台脱硝设备，因此脱硝成本计算公式如式(30)所示:

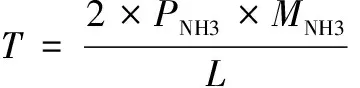
(30)

式(30)中，T为总成本，PNH3为喷氨量的单价(按市场价约3 500元/t)，MNH3为总喷氨量，L为机组负荷。

因此，在设置模型的奖励函数时，应兼顾喷氨量与脱硝效率之间的平衡关系。根据专家经验，当脱硝效率(η)处在85%～95%的合理范围区间，并同时满足总脱硝成本T是最小化时，应当给与奖励(reward=10)。其余情况下，都认为是不合理的，应当给与惩罚(reward=-20)。

DDPG模型的伪代码流程如下：

随机初始化Critic Q(s,a|θμ)和Actorμ(s|θμ)主网络参数，初始权重为υQ和θμ；

初始化目标网络Q′和μ′，初始权重为θQ′←θQ，θμ′←θμ；

初始化记忆库缓冲区大小为b；

for episode =1,...,M do

接收一个状态值st；

for t =1,...,T do

基于ε贪婪算法选择一个动作值at：以概率ε选择随机选择一个动作，否则以at=μ(st|θμ)的当前策略进行选择；

执行动作at，输入到Stacking-XRLL模型中，预测SCR出口NOx浓度，然后计算的脱硝效率η，最后再根据设定奖励规则，生成回报rt和新的状态值st+1；

将t时刻样本数据(st,at,rt,st+1)存储到记忆库b中；

当记忆库的数据存满，随机采样N个转换数据(si,ai,ri,si+1)，作为Actor、Critic目标网络的一个单位输入组数据集进行训练；

设置yi=rj+γQ′(sj+1,μ′(sj+1|θμ′)|θQ′)；

使用策略梯度更新Actor网络参数：

最后更新目标网络参数：

QQ′←νθQ+(1-ν)θQ′

θμ′←νθμ+(1-ν)θμ′)；

end for

end for

根据上述的DDPG算法伪代码流程，迭代训练500个周期，即过程通过不断调整评判者网络参数以修正行为网络的参数，直至Actor网络和Critic网络趋于稳定，进而优化燃煤电厂电站锅炉脱硝过程可控运行参数，使得基于Stacking-XRLL的多模型建模的SCR脱硝过程氮氧化物预测模型输出满足SCR脱硝出口NOX排放浓度(低于50 mg·m-3)、脱硝效率处于合理范围区间内(85%≤脱硝效率≤95%)以及总脱硝成本T最小化时，最终可以获得满足条件的最优可控动作参数集。

3 实验结果与分析

3.1 实验环境与数据

本文进行实验所需的硬件设备(计算机)配置如下：中央处理器：Intel(R)Core(TM)i7-9750H CPU @2.60 GHz 2.59 GHz；计算机内存：16 GB RAM；操作系统：Windows10-64位；图形处理器：NVIDIA GeForce GTX1660Ti 6 GB。

本文进行实验所需的软件平台包括：运用Python编程语言；编程环境：Python v3.7、Python IDEA：Pycharm v2020.1；Scikit-learn库：v0.22.1；numpy：1.19.4；pandas：1.1.4；matplotlib：3.3.2。

在进行实验时所需数据集是以广东某电厂1 000 MW电站SCR脱硝系统为研究对象，根据SCR系统运行状况和专家经验分析，从DCS信息数据采集系统中选取机组负荷、喷氨质量流量、SCR入口烟气O2量、SCR入口烟气温度、SCR入口NOX质量浓度、SCR出口NOX质量浓度等一共6个特征，数据如表1所示。其中可控变量：喷氨质量流量。状态变量：机组负荷、SCR入口烟气O2量、SCR入口烟气温度和SCR入口NOX质量浓度。输出变量：SCR出口NOX质量浓度。选取2018年4月1日-2018年4月30日时段内SCR脱硝系统机组稳态运行状态数据，每间隔为60 s采集一次数据，最终取10 000条样本作为模型的数据集。对从DCS系统采集到的样本数据集进行数据预处理，其中包括剔除异常值样本和筛选稳态工况。稳态工况可以利用滑动窗口法进行判断，如式(31)所示[20]：

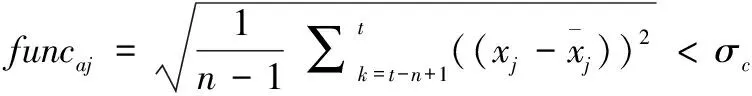
(31)

在式(31)中，其中n=35为窗口宽度，xj为归一化后的特征变量参数，可以选择机组负荷，σc=0.65为稳态工况的阈值。

3.2 MiniBatchKMeans工况聚类划分

从DCS系统采集10 000条稳态工况数据样本，按照4:1的比例划分训练集与测试集，同时保证训练集和测试集涵盖SCR系统各运行工况。经过与电厂专家交流分析后，将从DCS系统采集的6个特征变量作为模型的输入变量，SCR出口氮氧化物浓度作为模型的输出变量。设定初始聚类簇数值在[2,11]范围内，分别计算相应值下的轮廓系数，当聚类簇个数Cf=7时，总的轮廓系数最大，此时聚类效果最好，最终将训练集按机组负荷聚类为7个子簇。经过MiniBatchKMeans聚类所得工况聚类划分结果如表2所示。

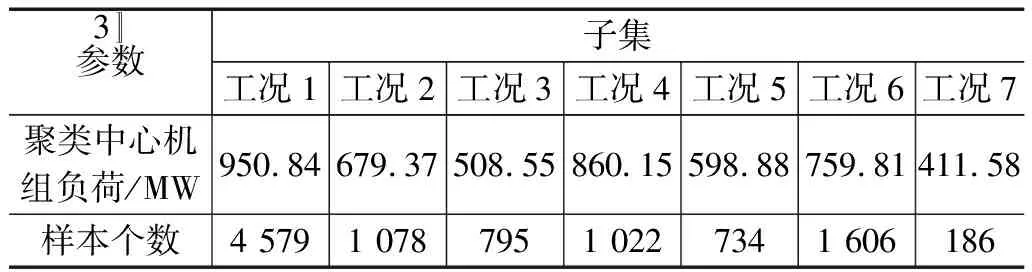
表2 工况聚类划分结果

3.3 多模型融合建模预测

对7个子集分别利用基于Stacking-XRLL多模型融合算法进行建模，将获得的10 000条样本数据，8 000条作为训练集，2 000条作为测试集。最后利用所建立的模型在测试集上进行预测，得到SCR脱硝出口NOX排放浓度预测结果如图4所示。采用模型评估指标：平均绝对误差(MAE)、均方误差(MSE)和决定系数R2对模型进行评价如表3所示。

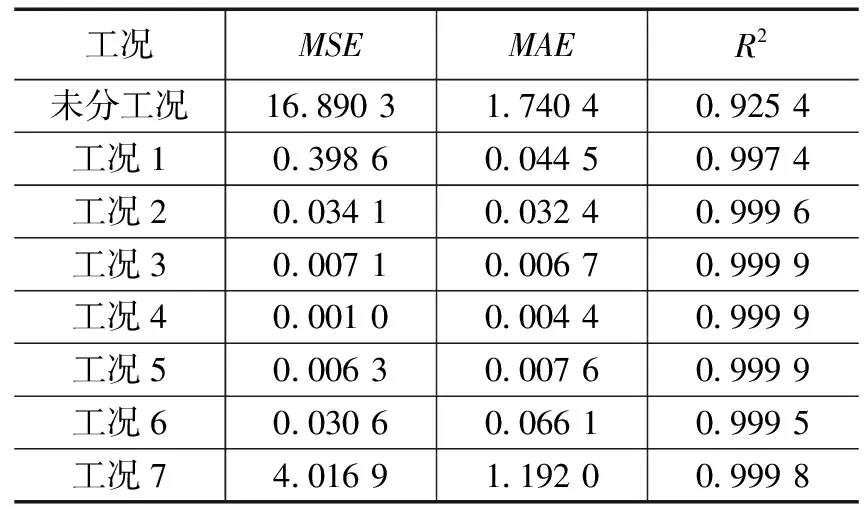
表3 不同工况模型预测结果性能对比

由图4与表3可知，对SCR系统的运行工况进行聚类划分之后，在每一个子集工况下分别利用基于Stacking-XRLL模型进行预测，实验结果表明，未进行工况划分之前，模型预测精度MSE(均方误差)=16.890 3、MAE(平均绝对误差)=1.740 4和R2(决定系数)=0.997 4。而锅炉运行工况进行聚类划分之后，在各个工况下进行预测，每一类工况下预测的精度都得到了提升，其中每个工况下总的均方误差MSE=0.642 0、平均绝对误差MAE=0.193 3和R2=0.999 4。

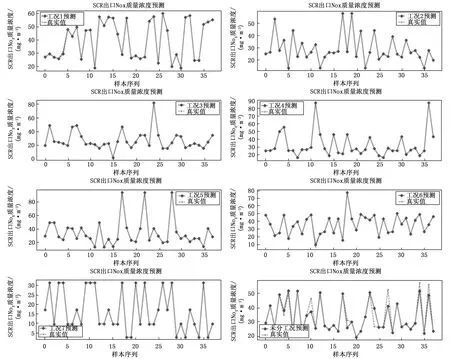
图4 不同工况下模型的预测结果

为了充分验证本文所提出的基于Stacking-XRLL多模型融合算法的有效性，从7个工况中随机选取工况2下的数据集，将其分别与单模型最优模型参数条件下的BP神经网络、LSTM神经网络模型、GRU神经网络模型进行对比实验，如图5所示。其中，BP神经网络为3层网络架构，第一层有256个神经元，relu为激活函数，dropout率为0.2；第二层有128个神经元，relu为激活函数，dropout率为0.3；第三层为全连接层。LSTM循环神经网络总共建立四层LSTM层，神经元个数分别为128、128、64和32，dropout率为0.3，tanh为激活函数，最后一层为全连层。GRU神经网络总共建立5层GRU层，神经元个数分别为128、64、256、256和128，dropout率为0.3，tanh为激活函数，最后一层为全连接层。

由图5与表4可知：在同一工况条件下，单模型BP神经网络要优于单模型GRU神经网络，而单模型GRU神经网络要优于单模型LSTM神经网络，但是基于Stacking-XRLL多模型融合算法，无论是精度上还是泛化性能上都优于BP神经网络、GRU神经网络、LSTM神经网络，其中MSE=0.110、MAE=0.030和R2=0.999。因此，实验结果表明：Stacking-XRLL多模型融合算法，能够有效且精准地预测电站SCR系统脱硝出口NOX浓度。

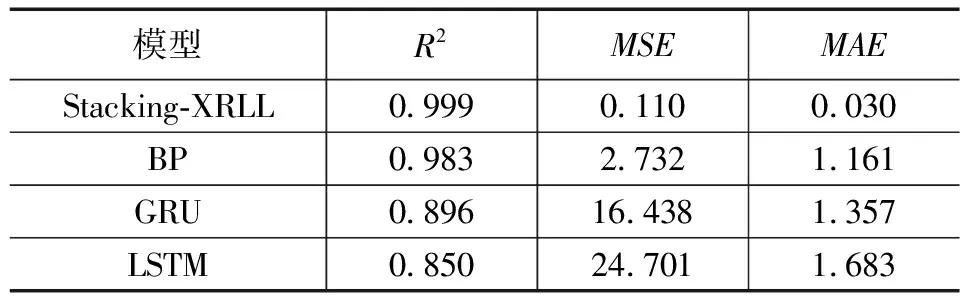
表4 同工况下不同算法之间的预测结果性能对比

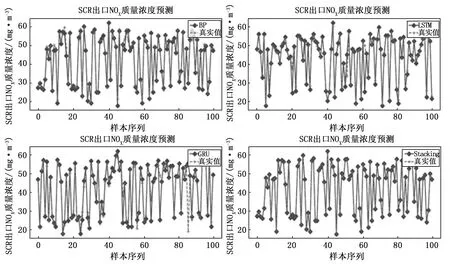
图5 同工况下不同算法之间预测结果对比

3.4 DDPG优化控制的结果

由4.3小节的实验结果，得出Stacking-XRLL模型预测的精度最优。因此，将Stacking-XRLL预测模型作为深度强化学习DDPG模型中的环境(ENV,Environment)，以工况1作为实验的数据集，经过反复实验调试，最终确定强化学习周期设置在500，每个周期100回合时，实验的收敛效果最明显，每回合取一个预测结果。当模型迭代训练稳定时，得到实验结果如图6中(a)～(d)所示。

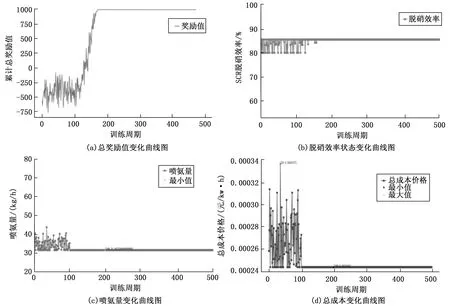
图6 硝过程参数优化控制结果图

从图6(a)～(d)实验结果可以看出，DDPG深度学习优化控制模型的总奖励值在200回合后趋于稳定。即当DDPG深度学习模型稳定时，模型的总奖励值由一开始惩罚到奖励，不断迭代训练，最终趋于最优值稳定。此时，脱硝效率值稳定在86%左右，处在合理范围区间之内，且可控参数喷氨质量流量稳定在35.657 kg/h，且经过优化之后，脱硝成本总价格降低了27.56%。

4 结束语

脱硝效率作为衡量SCR脱硝系统主要指标，对脱硝系统乃至整个发电机组都有着重大影响。实现准确预测脱硝效率，能够对机组的稳定运行和优化控制起到推动作用。将机组负荷、SCR入口烟气温度、SCR入口烟气O2量、SCR入口NOX质量浓度和喷氨质量流量等参数作为输入，基于Stacking-XRLL模型融合算法，构建深度确定性策略梯度网络优化控制模型，实现对可调运行参数的优化，得到不同工况下的最优操作参数值。基于某1 000 MW燃煤电厂机组实际运行数据进行仿真，结果表明通过优化后机组的脱硝效率稳定在86%左右，同时能满足脱硝出口NOX排放浓度要求以及总脱硝成本相比未优化之前降低了27.56%。