基于变步长算法的航天测控雷达多站跟踪技术研究

郑浩荣，蔡红维，张 瀚，罗 昊，王 康

(中国西昌卫星发射中心 技术部，四川 西昌 615000)

0 引言

随着现代化战争模式不断发展，战场环境复杂多变，武器种类日新月异，雷达功能亦随之日益丰富。雷达作为主要信息来源之一，实现多目标跟踪测量、远距离高速目标快速捕获、分辨真假弹头等功能已成为现代雷达的发展趋势[1-4]。

径向速度作为现代雷达测量目标特征的重要参量，对其的精确测量可提高测距精度、进行目标识别[5-8]。为了获得测量目标的速度信息，高重复频率体制雷达通常会被采用，以提高测速精度，消除速度模糊，但高重复频率意味着其距离测量是高度模糊的。在航天测控领域中使用的雷达往往综合测距、速、角等功能，当测量目标为高速飞行的航天器时，选取的重复频率不足以使雷达测速无模糊，因此必须进行解速度模糊操作。传统的快速傅里叶变换或多普勒滤波器组测速方法在面对低重复频率时有精度低、计算量大、解速度模糊效果差等缺陷[9-10]。此外，航天测控领域通常用雷达链实现对航天器的轨迹测量，因此测量雷达还需配置多雷达站的同时工作方式，多站工作是几部测量雷达同时向目标上的应答机发送询问信号，而要求雷达能够正常接收并跟踪应答机对本雷达的应答信号，并且不受应答机对其它雷达应答信号的干扰。

文献[11]提出了一种目标速度细谱线数字跟踪方法，通过获取测量目标加速度估计方法，结合复合控制技术进行解速度模糊，解算结果精度高，但该方法受到距离微分均值小于半个脉冲重复周期对应速度量的条件限制，应用范围较小且响应速度慢。文献[12]使用多站点测量数据相结合，经坐标变换求解某一点位目标径向速度，多站点联合测量的性质与航天测控相吻合，然而其提出了基于距离一阶差分近似求解方法结果精度取决于采样间隔，采样间隔大则解算结果不准确，采样间隔小则计算量增大。文献[13]提出了一种四重频脉冲串解速度模糊的方式，该方法需要高信噪比及正确的速度门测量作为前置条件，否则结果会出现较大误差。文献[14]提到的变重复频率法实现了更快的响应速度与更高的精度，但是其操作本身会进行变频率操作，这与航天测控多站工作中要求各雷达设备的重复频率相同的普遍要求不相符。

本文基于文献[14]提出的变重复频率方法，分析其对多站工作的影响，验证该方法在航天测控领域应用的可行性。在此基础上，结合试验级模拟，提出了一种变步长解速度模糊算法，相较于传统谱峰搜索方法，其无需遍历解模糊区间，极大的减少移相次数、提升解算速度、增强抗噪声能力，具有良好的解速度模糊性能。

1 现有解速度模糊方式

目前航天领域的单脉冲雷达中主要应用的解速度模糊有两种，一种是不变量嵌入法，这种方法比较成熟，只通过对接收回波进行数据处理即可。另一种方法是变重复频率法，这种方法需要改变发射重复频率，是数据处理与实际操作相结合的一种方式，下面对两种方法进行详细介绍。

1.1 改进的不变量嵌入法

不变量嵌入法的基本原理是将测速回路中的速度滤波值、速度预测值及速度微分值经过处理后，代入测距回路中,经过一定时间的迭代后，对测距回路的距离微分进行统计平均，其均值即对应相应的速度模糊根数[15]。

该方法的数学基础是当目标加速度运动时，目标k时刻目标的距离为：

Rk=R0+v0kT+0.5ak2T2

(1)

其Z变换为Rz，目标的速度为vk=v0+akT，其Z变换为vz，将vz通过拉普拉斯变换Hz后得到yz，对应时域信号为yk，将yk代入α-β滤波的距离跟踪回路中。

(2)

(3)

(4)

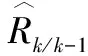
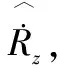
(5)

将Rz，yz代入，并令其为0，立即可得H(z)=(z+1)/2，对应的时域响应为：

(6)

同理如考虑加加速度(加速度微分)存在，可以证明此时yk可用下式代入：

(7)

1.2 变重复频率法

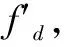
(8)

改变雷达的重复频率:

(9)

则:

(10)

当最大速度模糊仓数M小于(N/2-1)时，取

(11)

由上可知，该方法解速度模糊的范围有一定限制，所以在工程应用中，需要首先利用测距回路的距离微分得到的速度估计将目标的速度模糊范围缩小的一定范围，然后再采用此法进行解速度模糊。

两种方法进行比较，前者技术更加成熟一些，不足之处是其使用最小均分误差法进行迭代，解模糊的时间相对较长，同时需要一组额外的距离回路以防止与速度回路耦合，对信噪比的要求较高(一般要求大于等于20 dB)，后者的优点是解模糊时间短，对信噪比要求不高(9 dB左右)，缺点是当目标存在一定的加速度时，解模糊的正确概率下降，而且当目标存在距离模糊时，会造成回波丢失的问题。实际使用中，可以使用距离微分值对模糊范围进行约束从而提高正确率，并使用相位补偿的方式解决距离模糊时的回波丢失。

2 变重复频率对多站工作影响分析

航天测控是航天发射任务的眼睛，直接关系到航天任务成功与否。为保证航天发射过程中测控的精确测量、弹道选优、数据冗余和测控弧段连续性等指标，航天测控系统采用多个同频单脉冲雷达组成雷达链，从而形成了相互协同工作，又相互干扰的多站关系。

2.1 多站工作

在多站协同工作中，通常有两台或两台以上频率相似的雷达跟踪测量同一目标物，其信号都能够触发目标物上载有的应答机产生回波信号。由于多台雷达共用同一台应答机且应答机一旦触发就会有一段恢复时间，期间无法对到达的雷达信号进行回复，这导致如果多个雷达信号在应答机恢复时间内到达，则后至的雷达信号无法获取应答机的回波信号，造成应答信号遗漏。同时，回波信号来自同一副应答机天线，其频率、强度等特征一致，如果不同的雷达信号触发的回波信号时间上接近同一雷达的跟踪距离波门，该雷达将难以快速识别并跟踪自身信号[17]。

为防止上述情况发生，使多个雷达信号在时间上保持一定的相位差是十分必要的，因此加上一个时间卫门在雷达的跟踪距离门前端。通过不断检测卫门中是否有雷达的回波信号判断有无它站雷达发射信号接近本站雷达信号。如果在卫门中检测到它站雷达回波信号，本站雷达发射信号在时间上自动提前一个相位，进而避免两个雷达发射信号的接近造成的同频干扰现象发生。

2.2 变频率对多站工作的影响分析

使用变重复频率法时，需要进行变重复频率的操作，雷达在进行解速度模糊时，对方雷达站观察回波时，本雷达的信号会产生连续自动移相。具体情况视信号相对位置及自动移相方向不同可分为以下4种，如图1所示。

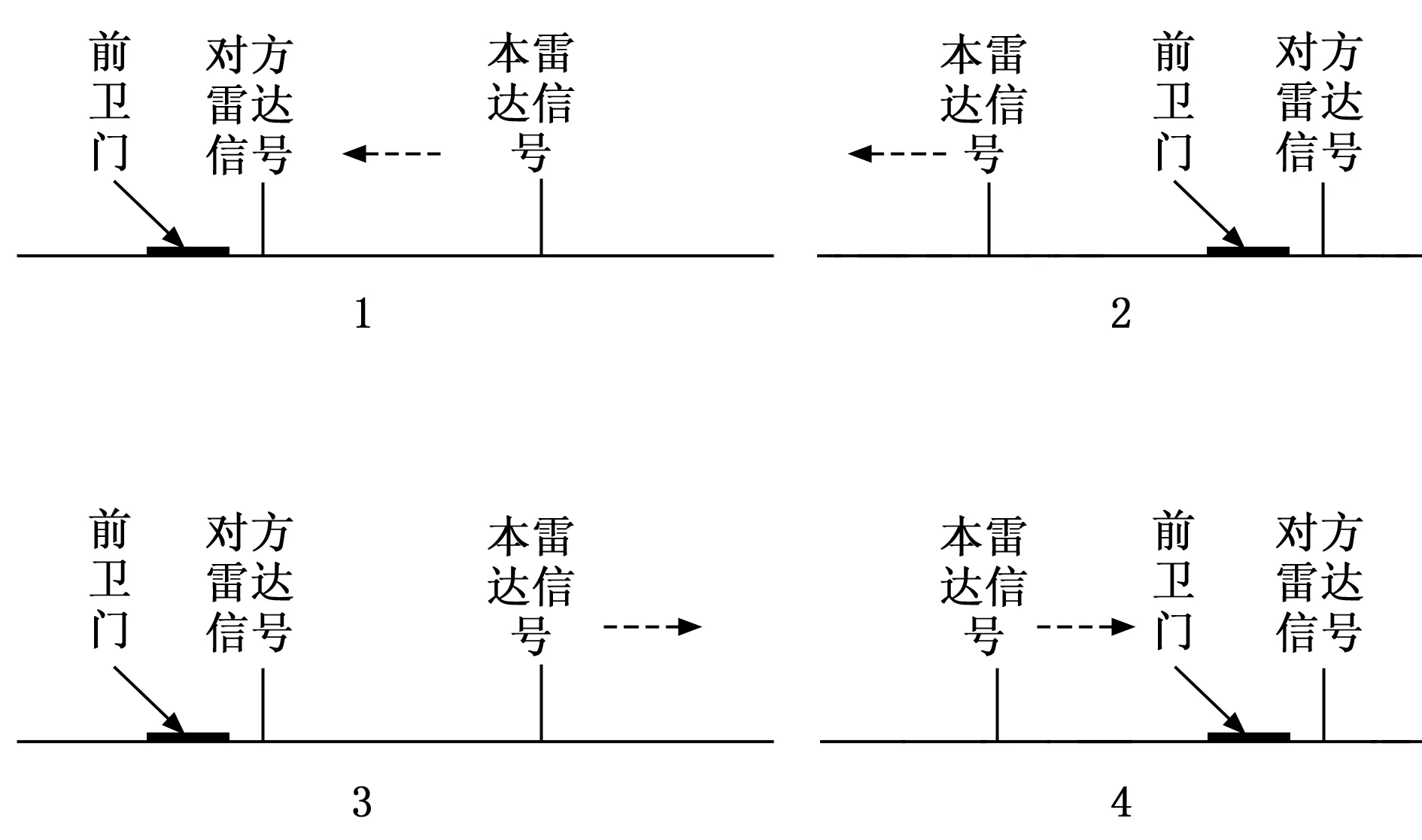
图1 对方雷达信号显示示意图

1)本雷达信号显示在对方雷达信号右侧，解速度模糊重复频率变大：本雷达的重复频率变大，在对方雷达信号上显示为干扰信号向左连续自动移相，一旦干扰信号进入对方雷达信号波门，由于对方雷达信号无后卫门，本雷达信号处于解速度模糊操作中，会导致对方雷达信号被阻塞或者本雷达解速度模糊中断，解速度失败。

2)本雷达信号显示在对方雷达信号左侧，解速度模糊重复频率变大：本雷达的重复频率变大，在对方雷达信号上显示为干扰信号向左连续自动移相，干扰信号远离对方雷达信号，但是本雷达信号如连续移相越过重复周期对应的最大距离，在对方雷达信号显示上相当于位于对方雷达信号右侧，情况如1。

3)本雷达信号显示在对方雷达信号右侧，解速度模糊重复频率变小：本雷达的重复频率变小，在对方雷达信号上显示为干扰信号向右连续自动移相，干扰信号远离对方雷达信号，但是本雷达信号如连续移相越过重复周期对应的最大距离，在对方雷达信号显示上相当于位于对方雷达信号左侧，当靠近对方雷达信号时，会触动对方雷达信号前卫门导致对方信号自动移相从而避免相互干扰。

4)本雷达信号显示在对方雷达信号左侧，解速度模糊重复频率变小：本雷达的重复频率变小，在对方雷达信号上显示为干扰信号向右连续自动移相，干扰信号靠近对方雷达信号，会触动对方雷达信号前卫门导致对方信号自动移相从而避免相互干扰。

综上所述，本雷达信号解模糊重复频率变大时，会存在解速度模糊失败和信号阻塞的风险。

2.3 实际情况分析

试验中使用两台雷达设备对同一目标进行跟踪，两设备工作频率为5xxx.x MHz，重复周期相同为5xx.x Hz，试验火箭上只有一台应答机，两设备采用变重复频率法解速度模糊。

模拟产生实战数据，经过事后处理，已知目标火箭的实际速度V如图2所示。

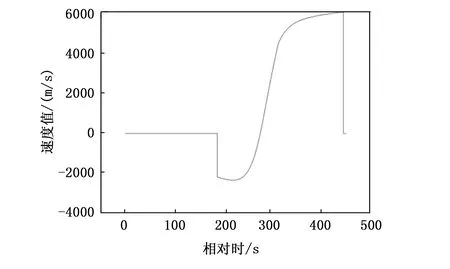
图2 火箭飞行径向速度

根据公式：

(12)

(13)

其中：fd为多普勒频移，f0为工作频率，M1为模糊谱线数，fr为脉冲重复频率。由公式(13)可以求出火箭实际飞行过程中的模糊谱线数，如图3所示。

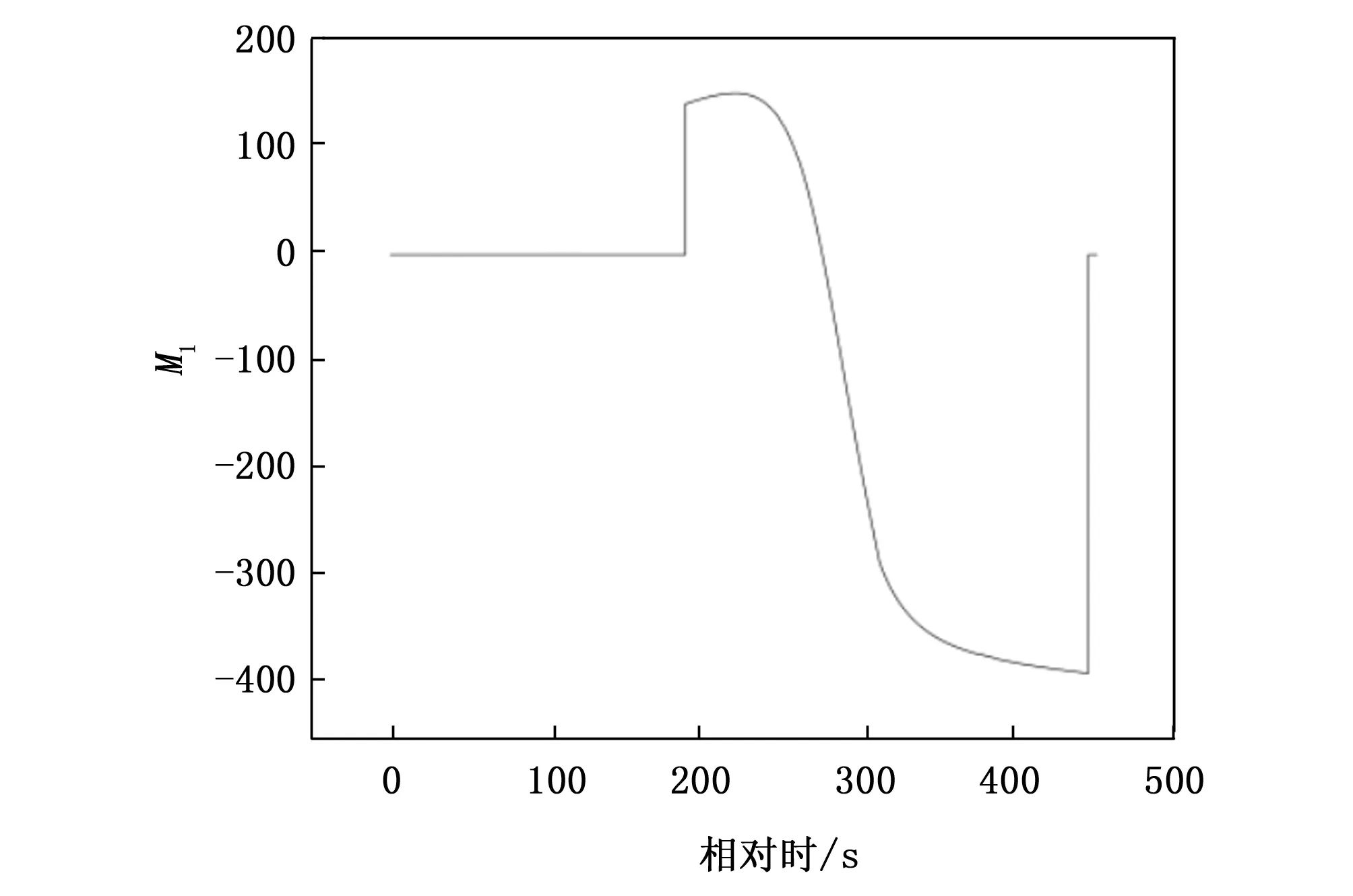
图3 火箭飞行产生的模糊谱线数

由图4可知，实际飞行速度所产生的模糊数M1范围在[-389,144]之间，想要对其进行变重复频率法的处理，最大需要发射778个重复脉冲，进行778次FFT运算，这显然是不合理的，所以需要对模糊数范围进行限制。

实际过程中，通过对距离测量值求微分，可以得到速度的估计值Vr如图4所示，并根据此估计值得到模糊谱线数的估计值M2，如图5所示。

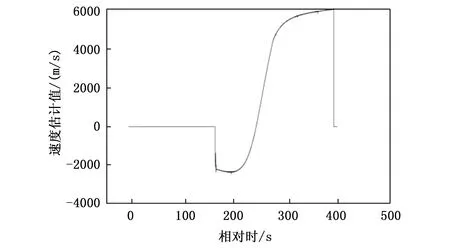
图4 径向速度估计值

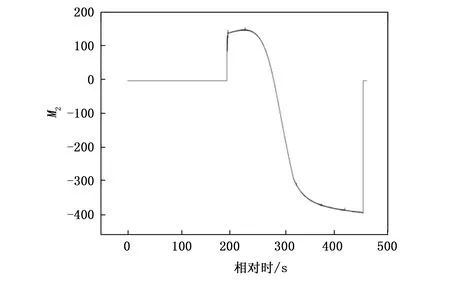
图5 模糊谱线数估计值

将图5与图3的值做差后取模，即可对实际模糊谱线数的范围缩减，缩减后的范围如图6所示。

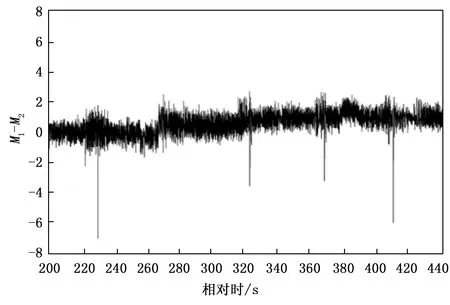
图6 模糊数差绝对值取模

如图6所示，模糊数的范围被缩减到了[-8,4]之间，取±8,即可包含模糊数的所有范围，实际情况中，该设备也是取±8两个值作为最大模糊谱线数进行计算，根据公式(9)分别求得外推周期为1.761 ms与1.654 ms，在指显系统上分别表现为右移8 km与左移8 km。

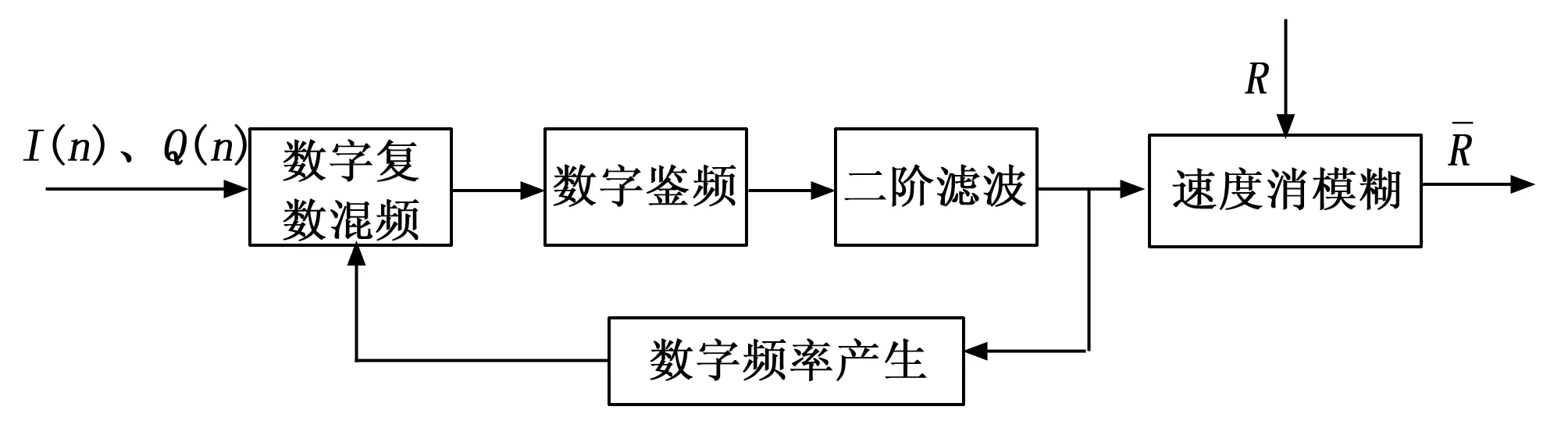
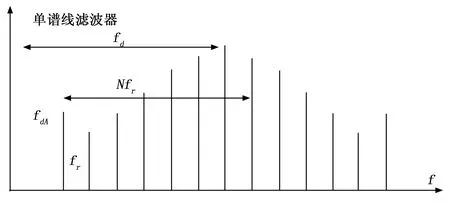
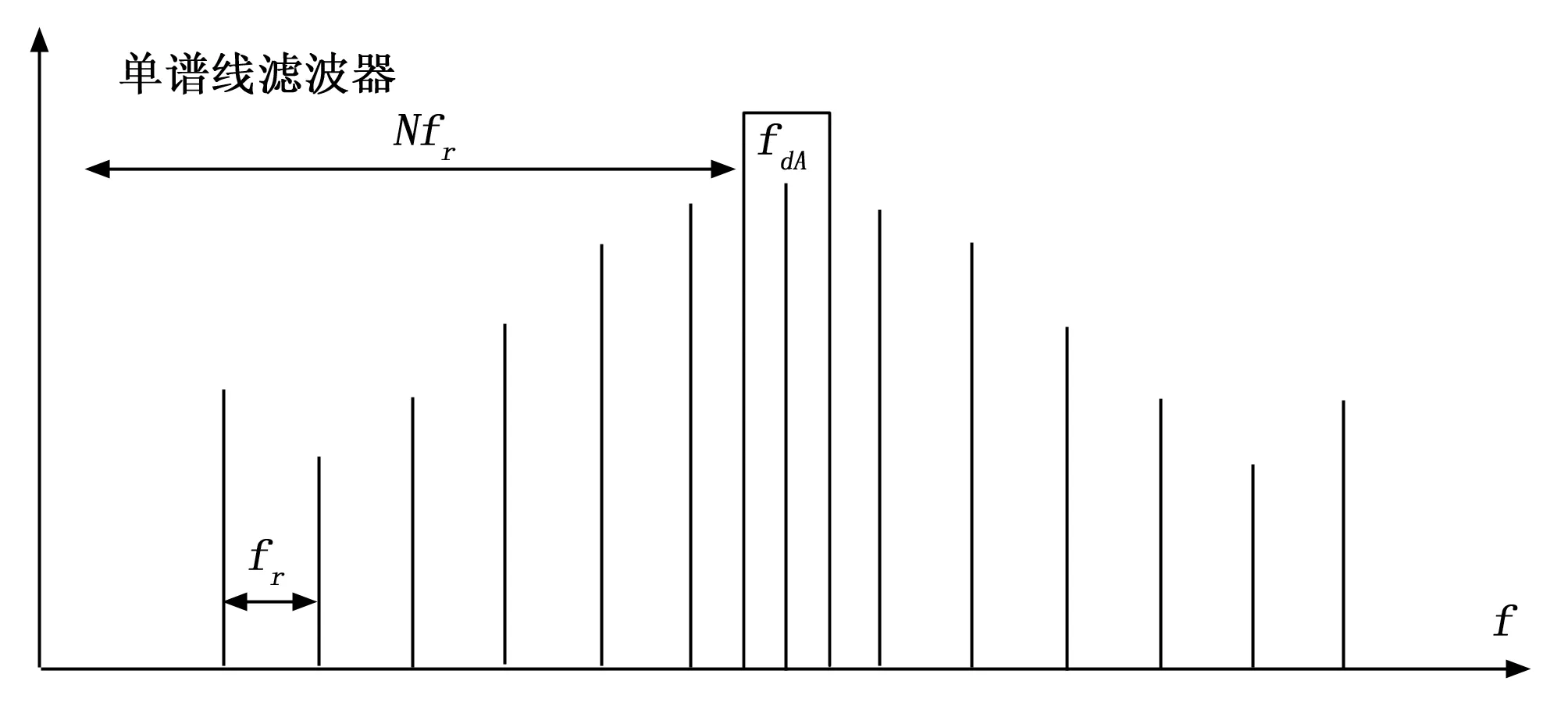
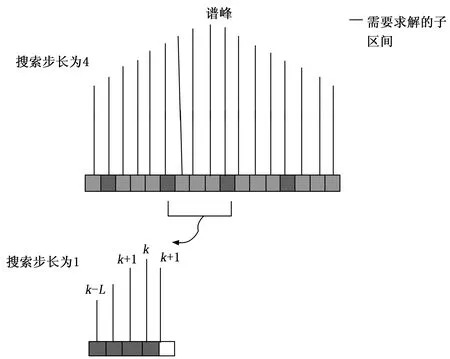
实际过程，当M1>M2时需要发射16个1.761 ms周期的重复脉冲才可以得到真实模糊数差，相当于连续向右移相128 km，对其它信号无影响，当M1

在试验中，确实出现了类似情况，造成其它设备的信号丢失，因此变重复频率法不适用于航天测控，为此新提出了一种变步长搜索解模糊算法，并对此进行了仿真验证。

3 变步长搜索解模糊算法

雷达速度跟踪回路原理如图7所示。

图7 速度测量回路原理框图

雷达接收机经正交采样后转换为基带信号I(n)、Q(n),通过两路数字混频分成两路滤波器进行数字鉴频,数字鉴频器的输出△U与输入信号的频率成正比,△U经α-β滤波后,调整反馈支路数字振荡器(NCO，numerically controlled oscillator)的输出频率,使其对准目标回波信号的频率,形成了一个闭环的频率跟踪系统。目标由于受雷达发射脉冲重复频率的限制,测速系统测出的目标径向速度会有模糊,通过消模糊得到精确的目标径向速度值[18-20]。

3.1 传统谱峰搜索原理

测速系统中雷达接收机接收的射频信号经速度测量回路混频后获取的信号的频谱图如图8所示，其中谱峰频率fd为无模糊多普勒频率，fdA为模糊多普勒频率，fr为脉冲重复频率，N为无模糊多普勒频率模糊度[21-22]，其关系如下式所示：

图8 单脉冲雷达频谱图

fd=fdA±Nfr

(14)

式中,fr已知，fdA值可在速度测量回路中获取，因此求取无模糊多普勒频率fd的关键在于求解模糊度N。

传统解模糊法采用移动滤波器的谱峰搜索方式。该方法将频谱图分割成K份子区间，每份长度为fr，即:

(15)

subsec(k)称为解速度模糊子区间。每当雷达接收机接收一次信号，单谱线滤波器的中心频率相应的向右移动长度为fr的距离，直至单谱线滤波器遍历处理完所有解速度模糊子区间的谱峰幅值测量。如图9所示，当单谱线滤波器向右移动到模糊度N所在的解速度模糊子区间时，其所测得的谱线幅值最大，即通过获取单谱线滤波器所测量的谱线幅值信息来判断正确的模糊度N，进而解算出速度模糊。然而该方法计算繁琐，实现困难，抗噪声能力低，因此设计了一种基于变步长谱峰搜索原理的解速度模糊方法。

图9 谱峰搜索

3.2 变步长谱峰搜索原理

传统谱峰搜索方法需要解算所有解速度模糊子区间，因此发射的重复脉冲较多，进行的移相次数较多，容易造成信号阻塞，如果能减少移相次数，则可以有效改善这个问题。此外，普通的搜索算法以单谱线滤波器输出谱线的幅值大小作为谱峰的判据，抗噪声性能较差，因为，当fr很小时，谱峰附近的几根谱线与谱峰相比，幅度相差不大，由于噪声的随机性，很容易产生临近谱线高过真实谱峰的情况，造成模糊数求解错误。基于这种思路，可以采用基于变步长谱峰搜索原理的解速度模糊方法，使用步长系数SM(k)作为检索谱峰的判读依据。

变步长谱峰搜索方法不需要解算所有的解速度模糊子区间，极大的简化了谱峰搜索流程。变步长谱峰搜索方法在混频信号的频率域内先用大步长对可能出现谱峰的区域进行初步检索，在确定范围后使用小步长对该区域进行进一步的搜索，直至确认模糊度N。根据混频信号的频谱具有偶对称的性质，建立步长系数SM(k)作为检索谱峰的判读依据。假定第K个解速度模糊子区间的步长系数为:

(16)

其中:Ma(i)为第i个解速度模糊子区间的谱线幅值，L为人为选定的步长参数。由上式可知，L值决定了步长系数SM(k)解算的解速度模糊子区间的个数，选取的L值越大计算结果越精确，抗噪声能力越强，但相应的计算量也会随之增加。在无噪声的理想情况下，包含谱峰所在子区间的步长系数计算结果应为1，然而雷达信号不可避免的会夹杂一些噪声信号使得步长系数计算结果偏离1。可以通过确保干扰噪声为白色噪声，使得谱峰所在子区间的步长系数比其他子区间步长系数更趋近于1。为了使步长系数能够更直观的表现，将式(16)改写为如下形式:

(17)

通过比较各解速度模糊子区间的步长系数的绝对值大小，更接近于0的子区间即为谱峰所在位置。

图10为变步长谱峰搜索算法示意图，图中中步长L先取值为14，搜索出谱峰所在的大致范围后再采用步长L为5进行搜索，进一步缩小范围后改用步长为1进行精确搜索。如图可知，7次搜索后即可找到谱峰，搜索效率极大提升，随着L取值越大，效率越高。

图10 变步长搜索算法示意图

变步长谱峰搜索方使用大步长检索时增加了谱线之间的幅度差值，能有效地降低系统噪声对谱峰搜索的影响，大幅提升了搜索效率。同时利用频谱偶对称性质，提高谱峰搜索精确度。

3.3 实际验证结果

利用Matlab软件进行仿真实验，仿真条件设置为航天器飞行速度3 000 m/s,脉冲雷达频率5xxx.x MHz，脉冲重复频率5xx Hz，自动移相距离为8 km，参与多站工作的单脉冲雷达数从1到10步进变化(各雷达相位距离一致)，在每种情况下，将速度模糊度N从0遍历到99，进行100次仿真试验。在上述假设条件下，对传统谱峰搜索方法和变步长谱峰搜索方法进行仿真，得到了多站工作雷达数与解模糊成功率的关系如图11所示。

将多站工作雷达数看做雷达协同工作能力，如图可知变步长搜索算法的协同工作能力是远强于普通搜索算法的。通过对航天测控雷达使用变步长解模糊搜索算法进行验证，其解模糊效果相较于传统谱峰搜索算法有明显提升，特别是在多站协同工作模式下，其解速度模糊成功率大幅增加。

目前国内航天测控领域协同工作的雷达数量在特殊情况下是多于四台的，在这种条件下，一旦出现突发情况需要进行解速度模糊，普通搜索算法极易出现解模糊失败的情况，而变步长搜索算法则大大提升了解速度模糊的成功率，有利于保障航天发射任务的顺利进行。

4 结束语

综上所述，变重复频率跟踪法在重复频率相同的多站工作模式情况下存在一定弊端，增加了信号阻塞和解速度模糊失败的风险。与航天测控领域中精确测控的要求不符，若将该技术运用到多站跟踪工作模式中，需对其进一步的研究和改进，消除其带来的负面影响。

为了提升航天发射领域在多站工作下模式下的解速度模糊精度和效率，本文提出了变步长谱峰搜索的方法，通过使用大步长检索确定谱峰大致区域后，缩小步长进行精确搜索谱峰位置，经过7次搜索后即可找到谱峰，从而判断正确的模糊度N，大幅度减少移相次数，提升了解速度模糊效率，且利用频谱偶对称性质有效减少系统噪声的影响，提高谱峰搜索精确度，降低了解速度模糊失败的风险。综合考虑了航天发射领域的多站工作模式，进行了传统谱峰搜索方法和变步长谱峰搜索方法在不同数量的雷达协同测控工作模式下的对照仿真实验。结果表明在多站协同工作模式下变步长谱峰搜索方法均比传统谱峰搜索方法有着更高的解速度模糊成功率，变步长谱峰搜索方法与当前航天发射领域适配。