基于深度强化学习的无人机空中目标自主跟踪
杨兴昊,宋建梅,佘浩平,吴程杰,杨钦宁,付伟达
(1.北京理工大学 宇航学院,北京 100081; 2.中国航空系统工程研究所,北京 100012;3.航天东方红卫星有限公司,北京 100094)
0 引言
无人机具有机动性强、成本低廉等优点,广泛应用于边境巡逻、目标打击、遥感测绘、农业植保、电力巡线等领域,但由于受载荷限制,其续航时间较短。若无人机能够在空中实现加油或更换电池等操作,则可以有效地提高无人机的续航时间和机动性能,同时减少燃油或电池的重量能让无人机承载更多有效载荷,从而提高其综合作业能力,因此空中对接在未来将成为无人机的基本技能。
实现空中对接前,主动对接无人机需要实现对目标无人机的持续跟踪,并保证两架无人机的相对位置在对接要求范围内,主动对接无人机称为主动无人机,目标无人机称为被动无人机。整个空中对接过程包括主动无人机对被动无人机的识别与相对位姿解算、主动无人机的精准对接控制两部分。具体过程为:当两架无人机相对距离较远时,通过GPS获取被动无人机的位置信息,并控制主动无人机接近目标。当两架无人机距离较近时,即当被动无人机清晰地出现在主动无人机机载摄像头拍摄图像中时,采用视觉算法对被动无人机进行识别与相对位姿解算。或采用精度较高的差分GPS获取被动无人机的位姿信息后进行对接控制。然而对接过程中GPS信号容易受到干扰,导致精度下降,因此目前的空中对接任务通常采用GPS与视觉混合的方式实现。
在无人机识别与相对位姿解算方面,传统的空中对接相对位姿解算过程中往往依赖于对特定锥套的识别,常用的方法包括:对锥套圆环的颜色进行改变[1-2]或在锥套上安装红外LED信标[3-4]。单尧等人[5]利用四旋翼无人机搭建自主空中加油演示验证平台,通过将无人机拍摄的锥套图像进行二值化处理后进行椭圆拟合,通过拟合椭圆与实际锥套尺寸进行比较以解算位置信息,并通过基于位置的PID控制器控制无人机进行对接。刘爱超等人[6]将对接装置的颜色与形状两种特征进行结合以设计对接锥套,首先利用被对接无人机的GPS/INS信息进行粗略导航,随后再利用视觉图标的颜色与形状信息实现精确导航,该方法能够保证在较高的飞行速度下仍然具有较好的跟踪效果,但当视觉图标出现遮挡、反光等问题时其跟踪效果有所下降。
在无人机精确对接控制方面,王宏伦等人[7]考虑了对接过程中的气流干扰与对接装置的自由摆动,针对空中加油对接段的精确控制问题,设计了基于线性二次线调节器的参考轨迹发生器和轨迹跟踪控制器,实验结果表明该方法具有快速性和一定的抗干扰能力,最终对接跟踪误差在0.2 m以内。李大伟等人[8]针对空中加油过程中软管锥套会受气动干扰而产生不规则摆动的问题,以线性二次调节器比例积分型控制器作为稳定闭环,并加入自适应控制器,从而提高控制过程中的抗干扰能力。黄永康等人[9]针对空中对接过程中纵向轨迹跟踪控制的时间滞后问题,提出一种基于直接升力的控制器,采用非线性 L1制导的方法,并基于ESO的动态逆方法设计飞控系统,以消除纵向轨迹跟踪的时间滞后,实现纵向轨迹的快速响应。朱虎等人[10]提出基于 L1 自适应动态逆的无人机自主空中加油对接跟踪控制方法,根据时标分离的原则,采用动态逆方法设计姿态回路控制器,并在回路中加入L1自适应系统补偿气流干扰和系统误差,该方法所设计的控制系统能够有效消除逆误差和气流干扰的影响。钱素娟等人[11]针对高速飞行中存在的对接装置振动问题,提出了基于辅助视觉的飞行器空中加油对接过程控制方法,通过统计飞行器空中加油辅助视觉图像出现共现的频率,计算对应图像在所有图像中的共现度,获取对应图像的权重,实现关键帧图像定位,运用图像中心点空间位置,建立近距空中加油时的尾流流场的气动影响数学模型,从而完成飞行器空中加油接口的定位。实验结果表明,在飞行震动较大的情况下该方法对接控制的准确度高于传统算法。
近年来,随着机器学习算法的飞速发展,深度学习与强化学习等智能算法也被应用到空中对接任务中。S.Sun等人[12]采用深度学习的方法实现对目标锥套的检测,同时完成相对位姿的解算。王宏伦等人[13]进一步研究了无人机软管式自主空中加油过程中的精准对接控制,利用CFD仿真获取气动数据,随后采用深度学习的方法对气动数据进行曲面拟合以获取干扰模型,并用循环神经网络预测对接装置的运动规律,从而显著提高了自主空中加油的对接精度。张易明等人[14]针对空中对接中的位置估计问题,提出了深度学习与双目视觉相结合的定位方法,对YOLOv4-Tiny进行改进,并在其基础上建立基于投影算子的模型参考自适应控制器,仿真结果表明该方法满足对接要求。王浩龙[15]采用近端策略优化控制方法以被动无人机的位置、速度等信息作为神经网络的输入实现飞行器的自主跟踪与对接任务。
上述研究将被动无人机的位姿估计与主动无人机的控制问题分开考虑,而本文研究了基于深度强化学习的无人机空中目标自主跟踪方法,实现了位姿估计与控制一体化,为空中目标跟踪问题提出了端到端的解决方案。采用近端策略优化算法(PPO,proximal policy optimization),将无人机搭载的摄像头拍摄的图像作为卷积神经网络的输入,不需在被动无人机上设置特定的视觉标识即可实现对空中目标的自主跟踪。
1 空中目标跟踪问题描述
1.1 空中目标跟踪的坐标关系与动力学建模
空中目标跟踪是实现空中对接的重要环节,空中对接任务由两架无人机配合完成,主动无人机需跟踪被动无人机一段时间,保证其相对位置与姿态在可对接范围内,随后控制主动无人机完成空中对接。本文主要研究空中对接前的空中目标跟踪,两架无人机的相对位置关系如图1所示,主动无人机在被动无人机后方跟随飞行。
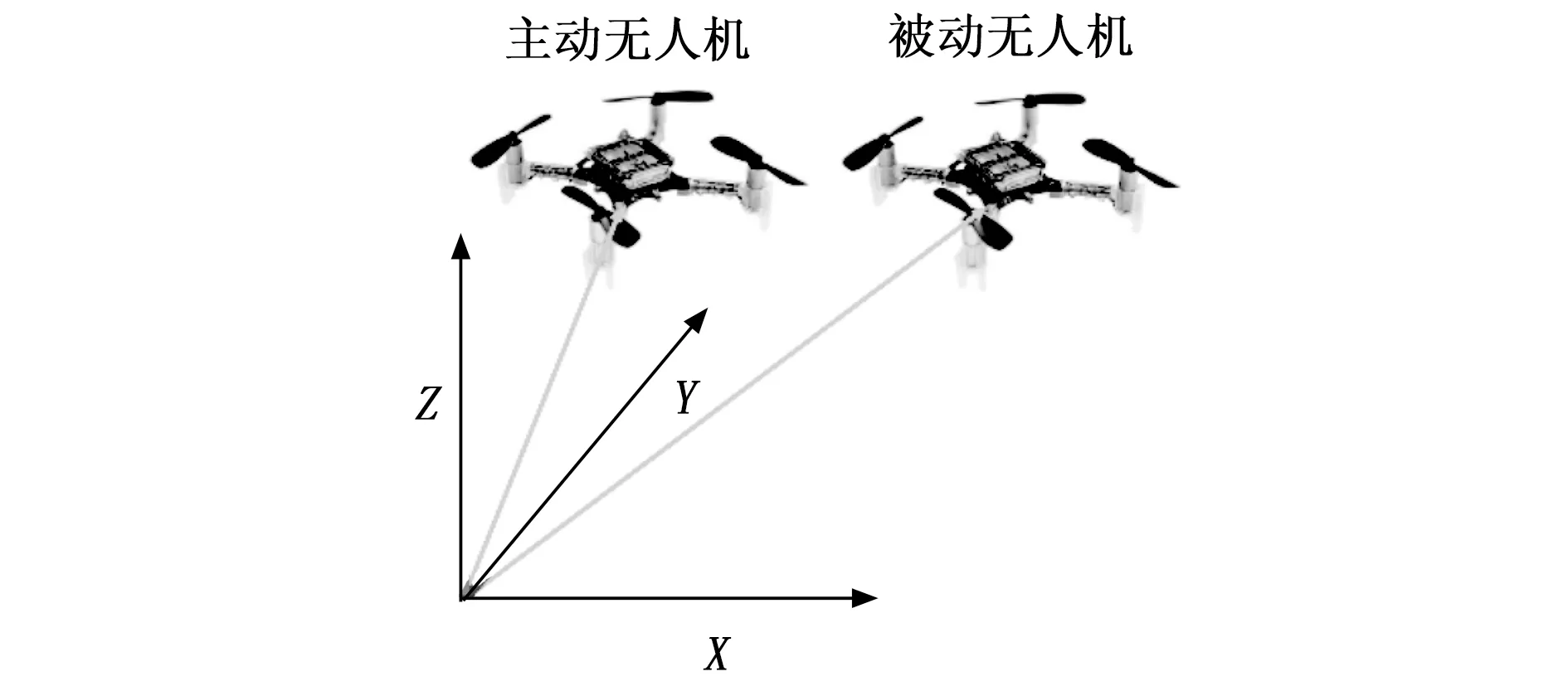
图1 相对位置关系
主动无人机与被动无人机均为“X”型四旋翼无人机,其动力学方程为:

(1)
式中,x、y、z为无人机在世界坐标系下的位置坐标,φ、θ、ψ分别为无人机的滚转角、俯仰角、偏航角,m为无人机的质量,F为无人机所受的合力值,Ix、Iy、Iz为转动惯量,Mx、My、Mz为螺旋桨升力产生的力矩。
本文选择“X”型四旋翼无人机,故其合力F与力矩Mx、My、Mz的计算方式为:
(2)
式中,Fi为各螺旋桨产生的升力,kF为螺旋桨升力系数,ωi为各电机转速,L为电机到质心距离,Mi为各螺旋桨产生的扭矩,kM为螺旋桨扭矩系数。
本文假设被动无人机沿世界坐标系的x轴正方向进行匀速直线飞行,其运动方程为:
(3)
式中,xtarget、ytarget、ztarget为世界坐标系下被动无人机的坐标,为被动无人机初始速度。
1.2 无人机PID控制器与强化学习
PID控制器具有算法简单、可靠性高的优点,因此在无人机控制中被广泛应用。作为无人机中的基本控制器,其结构如图2所示。

图2 无人机PID控制器结构图
强化学习是研究如何使智能体在某一环境下获取最大奖励值的一类问题,该问题可以用马尔科夫决策过程表示。马尔科夫决策过程的基本元素包括:智能体、状态空间S、动作空间A、状态转移函数P(SP′|S,α〕、奖励函数R。智能体是在环境中进行学习的个体。状态空间S是对环境信息具体描述的集合,其中某一特定状态用s表示。智能体通常无法获得环境中的全部状态信息,因此智能体在环境下获得的部分状态信息也可用观测空间O进行描述。动作空间A是智能体在环境下能够完成的所有动作的集合,智能体的动作用α表示。状态转移函数P(SP′|S,α〕为智能体在状态s下采取动作α后进入未来某一状态s′的概率。奖励函数R表示智能体在某一状态s下采取动α作后将获得多大的奖励值。
根据智能体所学习内容的差异,可分为基于策略的智能体和基于价值的智能体。基于策略的智能体直接学习策略函数π,通过策略决定要采取的动作α。策略函数π表示t时刻智能体在某一状态s下采取某一动作α的概率,即:
π(a|s)=P(at=a|st=s)
(4)
价值函数包括状态价值函数vπ(s)和动作价值函数qπ(s,α)。状态价值函数vπ(s)表示智能体在某种状态s时采用某种策略π后在未来能够获得多大的回报值G。回报值G是指未来能够获得的所有奖励值R进行折扣后的和,即:
Gt=Rt+1+γRt+2+γ2Rt+3+···+γT-t-1RT
(5)
其中:Gt表示t时刻获得的回报值,Rt+1表示时刻获得的奖励值,T表示结束时刻。γ表示折扣因子,其取值范围在0~1之间,γ取值越接近0时表示我们更加重视当前奖励,γ取值为1时表示未来奖励与当前奖励同样重要。
状态价值函数vπ(s)可表示为在状态s时采用策略π能够获得回报G的期望,即:
vπ(s)=Επ[Gt|st=s]
(6)
动作价值函数qπ(s,α)表示基于某种策略π时在某一状态S下采取某一动作α时所能获得回报G的期望,即:
qπ(s,a)=Επ[Gt|st=s,At=a]
(7)
策略函数π、状态价值函数vπ(s)与动作价值函数qπ(s,α)的关系可表示为:
(8)
基于价值的智能体通过学习价值函数从而隐式的学习策略,即从价值函数中推导出决定动作的策略。此时的策略π*为采取价值函数取最大值时的动作,即:
(9)
或
(10)
此时需通过遍历所有状态s和动作a找到最大化的价值函数或动作价值函数。
状态空间S是对整个环境世界的完整描述,包含环境内的所有状态信息。而观测空间O是智能体对状态空间的部分描述,不一定包含所有信息。当智能体能够观测到全部状态信息时,称为完全可观测的,此时状态空间S与观测空间O等效。当智能体仅能观测到部分状态信息时,称为部分可观测的。本文中的智能体为四旋翼无人机,其无法感知环境中的全部状态信息,因此其基于观测空间O选取动作a。下面依次介绍本文的观测空间O与动作空间A的设置。
观测空间O:将主动无人机摄像头拍摄的图像作为强化学习的观测空间O。与采用被动无人机位姿信息作为观测空间的方式不同,本文直接采用主动无人机摄像头拍摄所得的RGB图像作为观测空间。同时为加快训练速度,图像大小设置为64×48。
动作空间A:将经过PID控制输出的无人机期望速度作为强化学习的动作空间A。在强化学习训练过程中的每一步均需要传递一个动作以控制智能体,本文中的动作空间为无人机在世界坐标系下的期望速度:
V=[vx,vy,vz,vM]
(11)
式中,vx、vy、vz为无人机在世界坐标系下单位速度向量沿x轴、y轴、z轴的分量,vM为期望速度的量纲。此处根据文献[16]中的方法通过包含位置与姿态控制的PID控制器将期望速度V转换为各电机转速ωi。
2 深度强化学习算法与网络结构
2.1 空中目标跟踪的深度强化学习描述
基于深度强化学习的空中目标跟踪任务框架如图3所示,主动无人机作为智能体根据从环境中获得的观测信息Ot产生动作At从而实现与环境的交互,环境受到智能体的动作影响后进入下一状态,同时智能体获得新的观测信息Ot+1和奖励Rt+1,智能体获得新的观测信息Ot+1后产生新的动作At+1,不断重复上述过程直至完成训练。
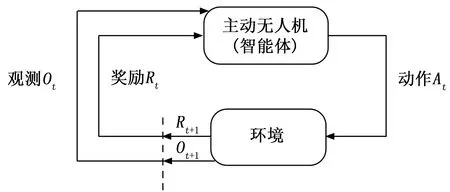
图3 强化学习框架
2.2 近端策略优化
强化学习中常用的策略梯度算法存在不好确定学习率与步长的问题。当学习率或步长过大时,策略网络不断振动而无法收敛,当学习率或步长过小时,策略网络的训练时间又过长。近端策略优化算法通过控制新策略与旧策略的比值,从而限制新策略的更新幅度,使其训练过程更加稳定。
近端策略优化是一种演员-评论家方法(Actor-Critic)。将基于价值的智能体和基于策略的智能体进行结合,同时学习价值函数和策略函数并将学到的两种函数进行交互从而得到智能体的最佳行动,采用该方法能够有效地加快学习速度,取得更好的学习效果。在演员-评论家方法中,演员指的是策略函数,评论家指的是价值函数。当智能体训练完成后,策略函数用于决定智能体的实际动作,价值函数则不再起作用,其仅供训练时为策略函数打分,使其学习到能够尽可能获得更高汇报的策略函数。
此外,采用深度强化学习方法能够同时解决感知与控制问题。强化学习方法仅能够对维度较低的状态信息进行处理以实现对智能体的控制,而深度强化学习方法能够直接对高纬度信息进行处理从而实现对智能体的控制,即同时解决了感知与控制的问题,更加接近人脑的处理方式。
当被动无人机的GPS信息无法获取或其无明显对接标识供视觉算法解算位姿信息时,采用深度强化学习的方法将主动无人机拍摄图像作为观测空间以训练智能体能够同时解决感知与控制的问题,不再需要单独解算被动无人机的位置与姿态信息。因观测空间为图像信息,因此策略函数和价值函数均采用卷积神经网络,分别称为Actor网络和Critic网络。
近端策略优化算法在更新Actor网络时有两种方法:KL惩罚和裁剪代理目标。下面分别介绍两种方法。
KL惩罚的目标函数为:
(12)
裁剪代理目标的目标函数为:
(13)
式中,rt(θ)为新策略πθ与旧策略πθold的比值,clip(·)为裁剪函数,ε为超参数。其中clip(·)裁剪函数表示当rt(θ)小于时,函数输出值为1-ε,当rt(θ)大于1+ε时,函数输出值为1+ε,即将函数的输出值限定在1-ε与1+ε之间,如图4所示。其中ε需要人为调节。
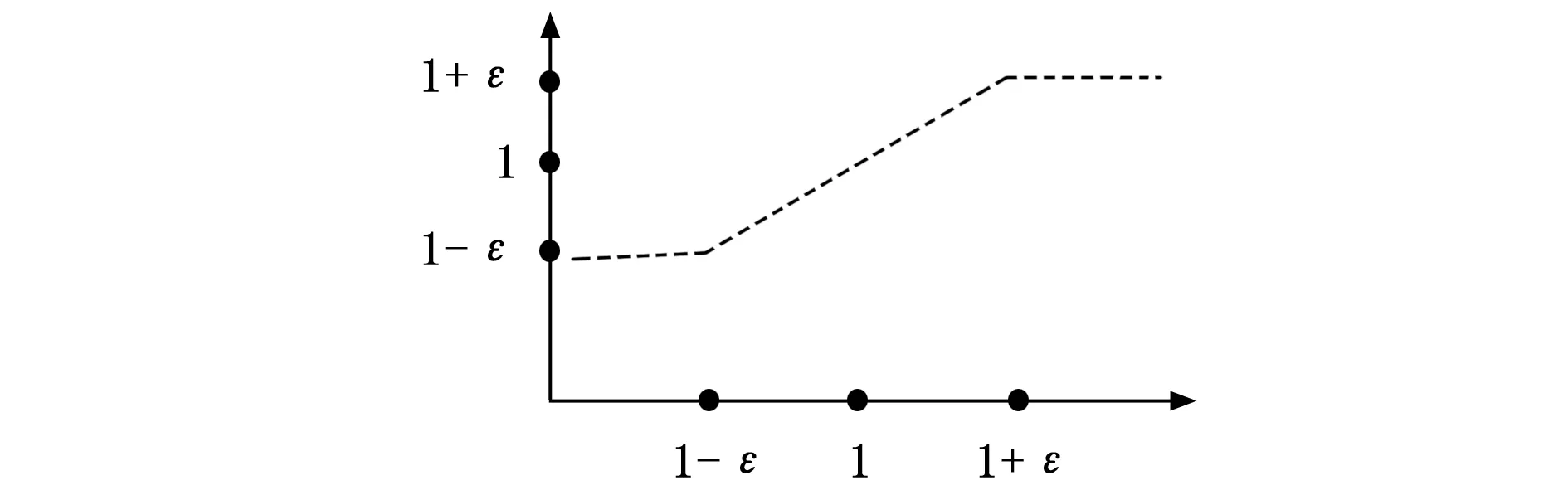
图4 裁剪函数
2.3 空中目标跟踪的网络结构
观测空间O为主动无人机摄像头所拍摄图像,如图5所示,即网络输入为图像,图像为高维度信息需通过卷积神经网络进行特征提取,因此Actor网络和Critic网络均采用卷积神经网络。

图5 对接无人机摄像头拍摄图像
文献[17]讨论了强化学习中“演员-评论家”类方法中Actor网络和Critic网络是否应分开的问题,结果表明当输入为图像等高维信息时,Actor网络和Critic网络间的参数共享较为重要,能够有效提取特征,同时减少计算量。因此本文的Actor网络和Critic网络共享前几层的网络参数,其网络结构如图6所示。
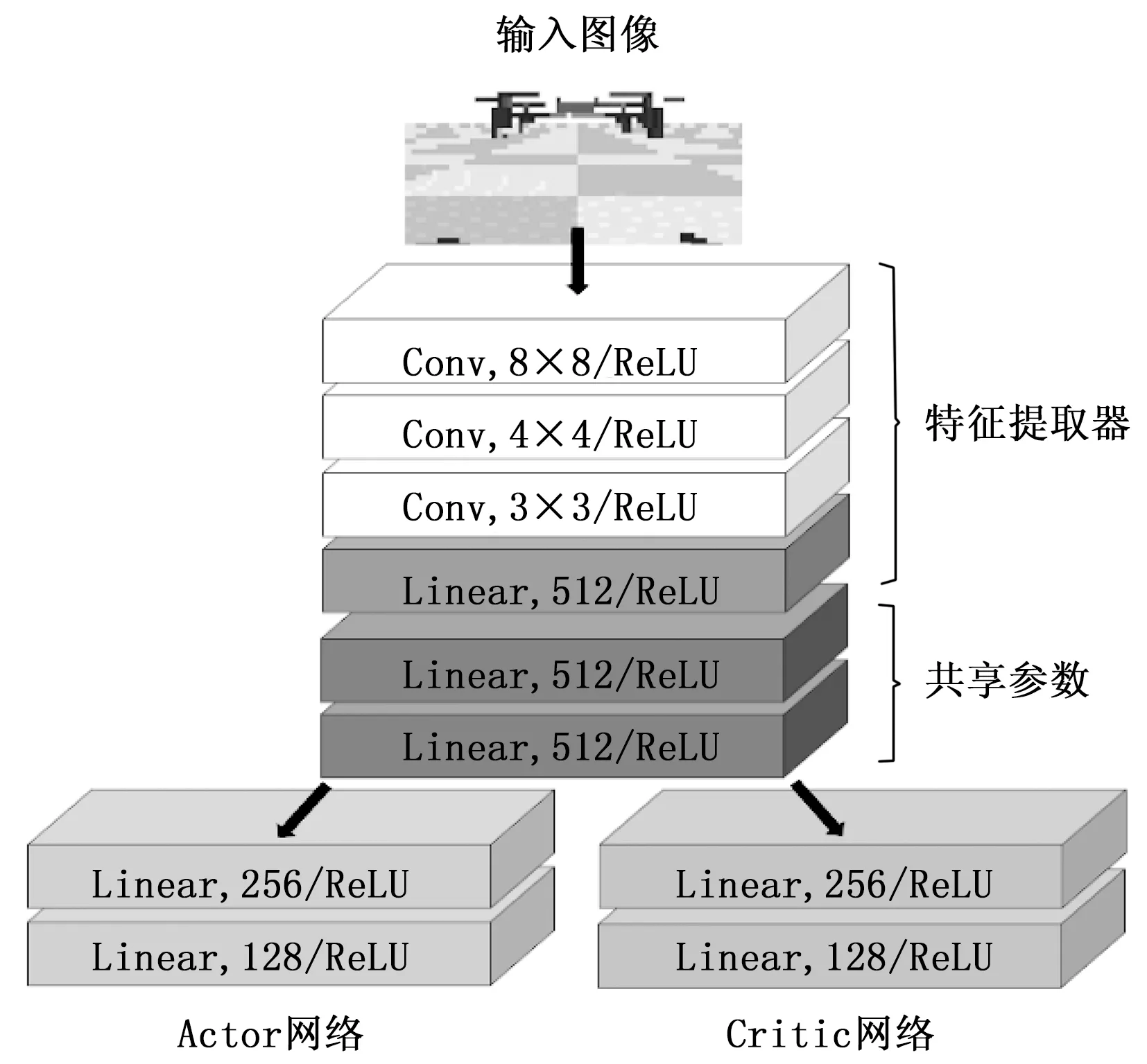
图6 Actor-Critic网络结构
网络主要由特征提取器和全连接神经网络两部分组成。特征提取器由三层卷积层构成,激活函数均为ReLU函数,卷积核大小分别为8×8、4×4、3×3,随后将卷积层输出数据拉平为一维数据,再经过节点数为512的线性层输入全连接神经网络。全连接神经网络首先由Actor网络和Critic网络共享的两层线性层构成,其节点数均为512,随后网络进行分支,共享层的输出分别进入Actor网络和Critic网络。Actor网络和Critic网络均由两层线性层构成,其节点数分别为256和128,Actor网络的输出为无人机4个电机的转速,Critic网络的输出为该电机转速下的价值函数。
2.4 空中目标跟踪的奖励函数
强化学习中需要设置合适的奖励函数以使得智能体能够完成所期望的目标任务,但在空中目标跟踪任务中如果仅采用最终是否跟踪成功作为奖励函数则会导致奖励太过于稀疏,使得最终训练效果不佳、训练速度缓慢。文献[15]中通过利用shaping的方法加速智能体训练,有效地解决了环境中奖励稀疏的问题并成功实现了无人机目标跟踪。为加快智能体的训练速度,本文也采用shaping方法设计奖励函数,此时奖励函数为:
rewardt=shapingt-shapingt-1
(14)
式中,rewardt为t时刻的奖励函数,shapingt为t时刻的shaping函数。即t时刻的奖励函数为t时刻的shaping函数值与时刻的shaping函数值的差。shaping函数为:
shapingt=
Vtrack
(15)
式中,xtarget、ytarget、ztarget表示被动无人机坐标,xagent、yagent、zagent表示主动无人机坐标。Vtrack表示无人机完成达到空中目标跟踪要求时获得的奖励值,即:
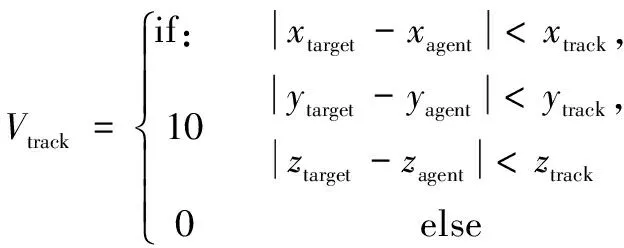
(16)
式中,xtrack、ytrack、ztrack表示跟踪要求范围。
3 空中目标跟踪仿真实验
3.1 空中目标跟踪实验环境
本文基于文献[18]中提出的开源四旋翼强化学习仿真环境进行开发。基于Pybuellt搭建仿真环境,Pybullet是基于Bullet进行物理仿真的Python模块。无人机模型选取“X”字型的四旋翼无人机Crazyflie,其相关物理参数见表1。

表1 Crazyflie物理参数
同时为使摄像头拍摄图像中的被动无人机更易识别,将被动无人机进行适当倍数的放大。搭建的仿真环境如图7所示。

图7 基于Pybullet的无人机跟踪仿真环境
硬件环境:GPU为英伟达2070 Super,CPU为英特尔i5-10400F。深度强化学习框架选择Stable Baselines3,其是基于Pytorch和Gym的强化学习实现工具,集成了一系列强化学习经典算法,包括:A2C、DDPG、PPO、SAC、TD3等。本文中强化学习算法选取近端策略优化(PPO)并采用裁剪代理目标的方式更新神经网络参数,相关超参数见表2。
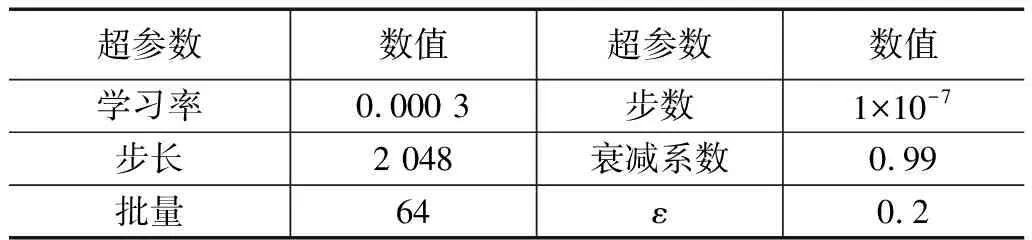
表2 PPO算法相关超参数
仿真环境中被动无人机沿世界坐标系x轴的方向进行匀速直线飞行,其初始位置为:

初始速度为:

主动无人机初始位置为:

主动无人机摄像头拍摄的图像作为观测O输入Actor网络中,Actor网络输出动作A,A为经PID控制后输出的4个电机转速,从而控制主动无人机自主跟踪被动无人机。跟踪条件为:

即主动无人机在世界坐标的x轴方向与被动无人机相对距离小于1 m,在y轴和z轴方向距离小于0.1 m时,便视为跟踪成功,此时将获得数值为10的跟踪奖励Vtrack。
3.2 空中目标跟踪实验结果分析
训练结束后利用训练过程中的最优模型进行仿真测试,仿真时间持续6 s,测试情况如图8所示。图8(a)为仿真初始时刻两架无人机间的位置关系,图8(b)为初始时刻主动无人机摄像头所拍摄的图像,图8(c)和图8(d)分别为仿真结束时刻两架无人机间的位置关系与摄像头拍摄图像。由图8可以看出最终两架无人机保持着较近的跟踪距离[19-20]。
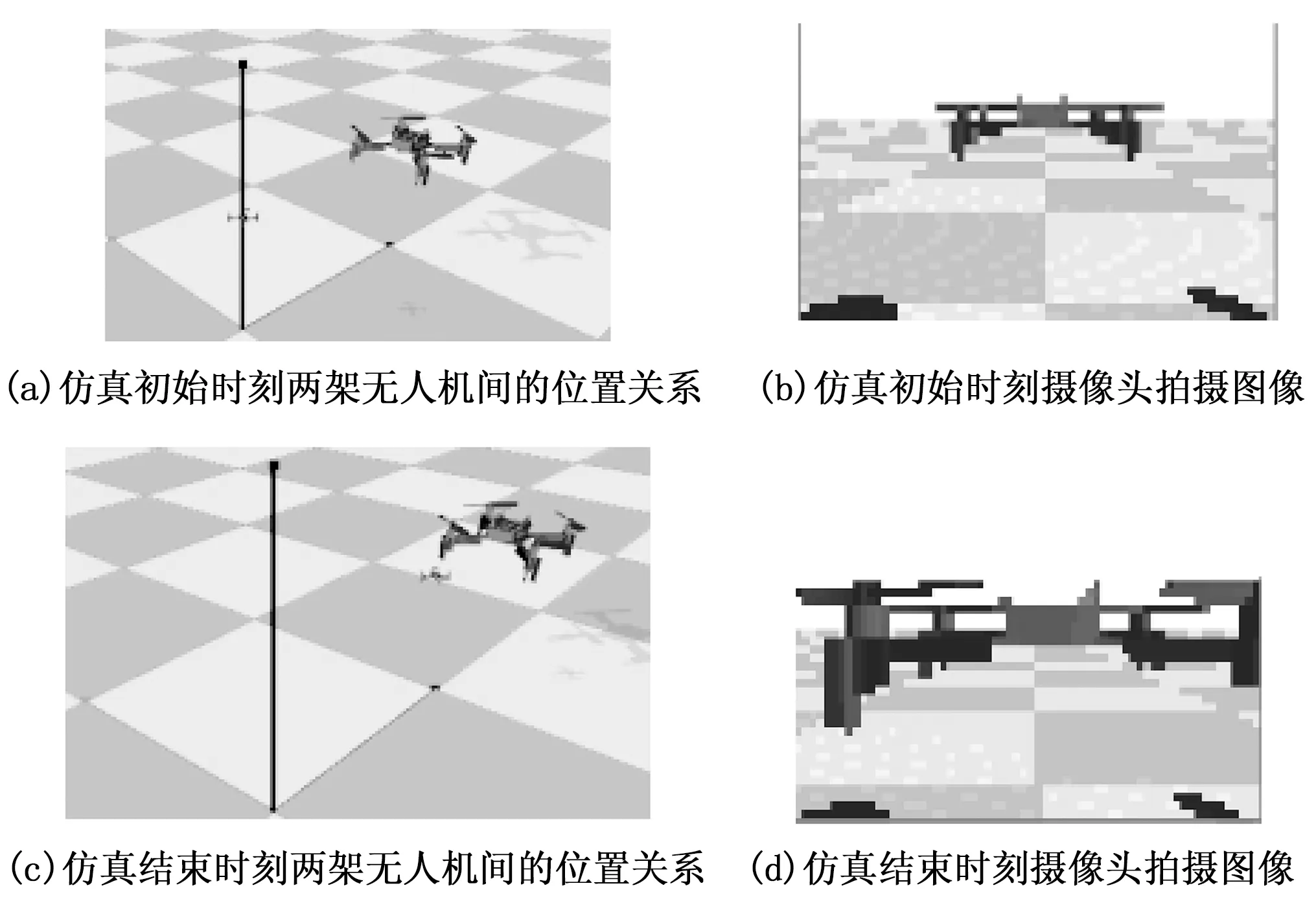
图8 仿真测试
空中目标跟踪仿真实验结果表明,本文采用PPO算法进行的空中目标跟踪能够达到跟踪要求,经过6 s的仿真测试最终沿世界坐标系x轴的跟踪距离最终保持在0.5 m左右,y轴跟踪距离在0.03 m以内,z轴跟踪距离在0.01 m以内。主动无人机与被动无人机间的位置关系与速度关系如图9和图10所示[21-22]。
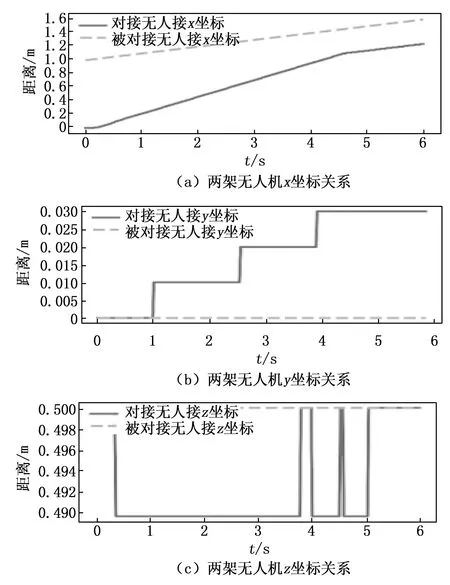
图9 两架无人机间的位置关系
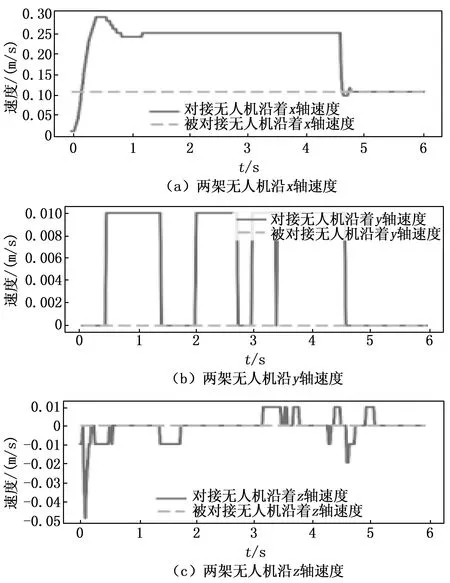
图10 两架无人机间的速度关系
从图9和图10可以看出被动无人机沿x轴正方向以0.1 m/s进行匀速直线运动,主动无人机沿x轴从静止开始加速到0.25 m/s匀速运动,当两架无人机间距离接近0.5 m后进行减速,并保持与被动无人机相同速度进行飞行。同时主动无人机在y轴与z轴的位置与速度存在较小震荡,但最终基本稳定[23-24]。
主动无人机姿态角与角速度如图11和图12所示。由图10(a)可以看出,初始阶段主动无人机需进行加速从而缩短与被动无人机间的距离,当速度达到0.3 m/s后进行减速,直至速度为0.25 m/s后进行匀速运动,当两架无人机距离达到0.5 m左右后减速至0.1 m,并保持跟踪。因此主动无人机俯仰角与俯仰角速度需相应变化,由于本文的仿真环境中未考虑空气阻力,因此匀速运动状态姿态角均为0°。但由图11和图12可知,姿态角在跟踪成功后存在一定波动,即不能保持与被动无人机的姿态角一致,因此在进行对接操作时还需考虑姿态角与姿态角速度的相对关系。
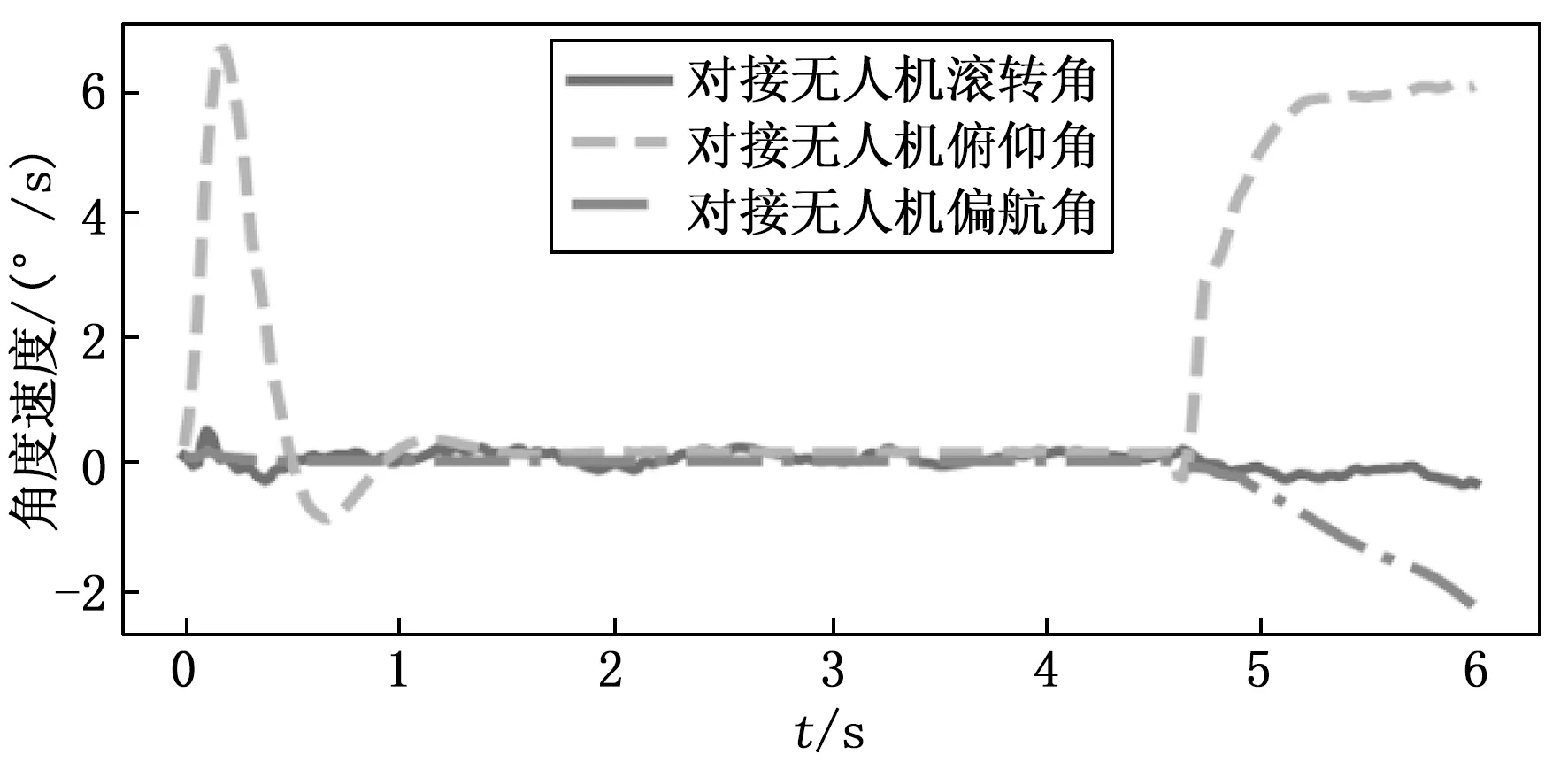
图11 对接无人机姿态角变化

图12 对接无人机角速度变化
仿真实验结果验证了采用深度强化学习的方法能够在仅输入主动无人机摄像头拍摄图像的情况下实现空中目标自主跟踪任务。该方法不需要通过GPS等传感器获得被动无人机的位置信息,也不需通过视觉算法对拍摄图像进行处理以解算被动无人机的位姿信息,通过端到端的方式即可实现空中目标自主跟踪任务[25-26]。
4 结束语
本文针对空中目标自主跟踪问题,提出了一种基于深度强化学习的技术方法。主要贡献在于:提出了端到端的空中目标自主跟踪方法,通过将深度强化学习方法应用在空中目标自主跟踪领域,将无人机摄像头中拍摄图像作为输入,Actor网络接受图像并输出4个电机的转速,从而控制无人机完成对空中目标的跟踪任务,无需获得目标位置信息,也不需额外设计图像处理算法,即可完成端到端的空中目标跟踪,提高了无人机的自主性与智能性。
本文仍有不足之处:实验中未考虑风阻力,也未考虑主动无人机与被动无人机间的相对姿态关系,仅适用于与相对姿态无关的空中目标跟踪任务,若需进行空中对接仍应进一步考虑两架无人机间的相对姿态与相对角速度关系。在未来的研究中将进一步考虑风阻力、两架无人机间的相对姿态与相对角速度关系。

