基于分数匹配生成模型的无透镜成像方法

伍春花，彭 鸿，刘且根，万文博，王玉皞

（南昌大学 信息工程学院，江西 南昌 330031）

1 引 言

基于掩膜的无透镜成像系统通过在图像传感器前几毫米处放置一个薄掩膜来替代镜头组件，直接应用图像传感器（如CCD和CMOS）记录场景信息，从而简化光学硬件[1-3］。该成像方式打破了场景到图像一一对应的采样方式，将成像的重心由硬件转移到计算上，使三维荧光显微镜、热成像和重聚焦摄影等成像系统实现结构紧凑化、轻量化、低能耗和低成本成为可能。在过去几年里，研究人员提出了各种各样的基于无透镜相干系统的成像技术，如，相干衍射成像[4-5］和片上显微镜[6-7］等。然而，这些成像技术对光的相干性要求很高，极大地限制了成像系统应用。

菲涅尔非相干全息术是新发展的一种非相干光成像技术。非相干光成像技术最早起源于20世 纪90年 代，Mertz和Young[8］提 出 了 用 菲 涅尔波带片（Fresnel Zone Aperture，FZA）编码全息成像的建议，将全息成像的概念和应用范围拓展到了非相干光领域。与相干成像技术相比，非相干成像技术的照明光源获取容易，且记录过程不会产生类似于激光全息术中固有的散斑噪声，可以有效提高再现图像的质量。因此，非相干技术在荧光三维成像、非相干全息三维显示、自适应光学、天文成像等领域具有独特的应用优势[9］。在无透镜成像系统中，使用非相干光照明将场景中无数个点光源线透过FZA，这些点源投影在传感器上非相干叠加后最后形成了编码图像。理论上，编码图像既包含物体振幅/透射率的信息，又包含相位延迟的信息。由于图像传感器只对入射光强度敏感，在图像采集过程中只能采集图像的强度信息而丢失了相位信息，这导致重建图像中出现物体的孪生像[10-12］。孪生像是同轴全息中的固有问题，表现为重建图像中会有物体的共轭像叠加在原始图像上，从而导致重建图像质量下降。

为克服无透镜成像中的孪生像效应，通常采用四步相移法来去除孪生像。该方法需要采集经过四组不同相位波带片的编码图像[13-14］，在实际操作中，不仅需要更换波带片，而且需要图像间的配准，增加了实验的复杂性。为了弥补这个缺点，可以采用单张FZA实现无透镜成像系统的编码，这样既不需要波带片和传感器之间的校准，又能简化实际操作。然而，使用单张FZA编码方式并不能消除孪生像，因此需要通过重建算法消除孪生像的影响。

针对无透镜成像过程因丢失相位信息导致重建图像不唯一的问题，如何建立场景与图像之间的联系，并通过求解逆问题反演图像是解决编码成像问题的关键。传统方法是直接通过使用反向传播（Back Propagation，BP）算法对同轴全息图进行重建，然而孪生像干扰严重影响了重建图像。正则化技术，特别是压缩感知（Compressive Sensing，CS）理论中提出的基于稀疏的全变分（Total Variation，TV）正则化方法是处理这种不适定问题的有效方式。2009年，Brady等[15］首次将压缩感知理论应用于全息成像中，实现了单幅全息图的深度重建和孪生像的去除。Wu等[16］根据孪生像和原始图像在梯度域稀疏程度的不同提出一种基于CS的无透镜成像方法，它通过在目标函数中加入TV正则化约束以改善问题的不适定性。在图像处理和计算成像技术中，通过外加约束先验的稀疏性在逆问题中可以增强图像统计的先验信息。虽然正则化先验技术常被用于不适定问题的求解。然而这类人为选择的正则化器存在校准误差和手动调整参数等不定因素，并不能表示真正的数据。

近年来，基于分数匹配生成模型[17-19］和去噪扩散概率模型（DDPMs）[20-21］的新的生成模型[17-21］引起了人们的广泛兴趣，它在不需要对抗训练的情况下能够实现高质量的样本。生成模型本质是用一个已知的概率模型来拟合所给的数据样本。虽然神经网络（Neural Networks）也能拟合任意函数，但是概率分布有“非负”和“归一化”的要求，因此不能随意拟合一个概率分布。近来，Song等人[22］提出了一个新的基于广义离散分数匹配方法模型。该模型通过概率密度函数对观察到的样本进行数据建模，在利用已知输入不变性建模数据分布方面表现出了出色的性能。生成模型在拟合参数学习的过程会尽可能地增加数据的相似度，因而可以学习良好的先验信息。近年来，有不少该领域的研究工作聚焦于如何更好地利用算法提升来改善成像质量，尤其是针对深度重构的真实度。基于此，本文利用生成模型强大的先验信息建模能力和成像的拟合约束相结合的方法，将生成模型引入到无透镜成像逆问题求解。本文提出一种基于分数匹配生成模型的无透镜方法（Lens-less imaging via Score-based Generative Model，LSGM）。具体而言，无透镜成像系统在非相干照明下使用单张FZA实现点源编码，无需精确校准和严格标定，具有更高的信噪比。然而，由于孪生像的伪影很容易导致重建质量差以及颜色重建不准确等问题。针对这个问题，本文提出一种新的LSGM算法对编码图像进行解码重建。该模型通过利用梯度数据分布对图像样本进行建模，并从给定的观测数据的条件分布中采样数据，然后将采样的数据作为先验信息和成像的拟合约束相结合来求解无透镜成像的逆问题。该方法模型训练稳定、结构灵活，在数据分布建模方面表现出了强大的性能，并且能获得丰富的先验信息，可以有效地用于无透镜成像中逆问题的求解，并有望扩展至其他计算成像领域。

2 基本原理及算法过程

2.1 无透镜成像原理

如图1所示，无透镜成像的主要流程主要包含两大部分：光学编码和计算解码。不同于传统光学成像——“所见即所得”。无透镜成像直接应用图像传感器记录由编码掩膜调制的场景信息，然后通过算法重建场景图像。

若将FZA的透射率函数近似为理想波带片，其振幅传递函数为：

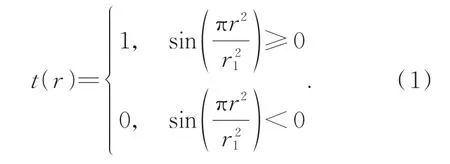
对式（1）作傅里叶展开为T(r)=[1+cos(πr2/r21)]/2。其中：r=(x，y)；r1为常数，表示FZA最内侧区域的半径。然后根据欧拉公式转化为：

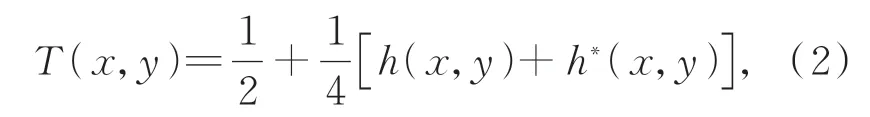
其中：h(x，y)=exp(i(π/r21)(x2+y2))，h*(x，y)是h(x，y)的共轭。当r21=λd时，h(x，y)与菲涅尔传播核函数exp(i(π/λd)(x2+y2))相同。

目标物体被放置在离FZA一定距离处，在非相干光源照明下，经过FZA调制的所有点源叠加的集合被传感器捕获。其成像过程的表达式即为目标图像与FZA函数的卷积：

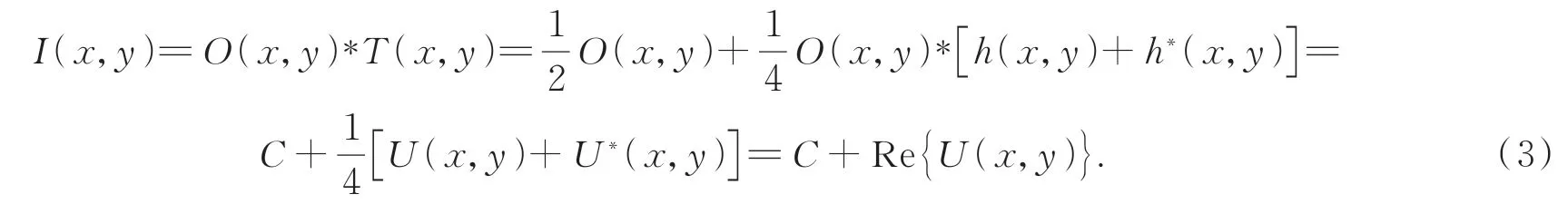
其 中：*表 示 卷 积；O(x，y)为 目 标 图 像；U(x，y)=O(x，y)*h(x，y)可以看作是波长为λ的光波在距离d处传播的衍射波前图像；U*(x，y)与U(x，y)相互共轭，式（3）中U*(x，y)相关的项即为孪生像；C为常数，可直接通过直流滤波去除。将上式卷积计算转换到傅里叶频率域，计算公式表示为：

其中，I∈RNxy为传感器测的图像数据；O∈RNxy为目标图像；F和F-1分别为傅里叶变换算子和逆傅里叶变换算子；H表示乘以传递函数H=i exp(-iπλz(u2+v2))的操作算子。由于O为实函数、H为中心对称函数，则Re{H}=sin(πr21(u2+v2))是cos((π/λd)(x2+y2))的 归一化傅里叶变换。假设系统转换矩阵H=F*ΛF，其中F∈RNxy×Nxy为二维离散傅里叶变换矩阵，Λ为对角矩阵，其非零项为Re{H}的离散值。则用O表示I的相关函数即为正向转换模型：

其中，H为系统测量矩阵或者传递函数矩阵。上述正向模型是一个典型的逆问题。在式（3）中，U(x，y)的虚部可以被任意赋值，使得求解不唯一，从而产生孪生像。孪生像的伪影很容易导致重建质量差以及颜色重建不准确等问题，引入合适的图像先验是解决该问题的关键。

传统的方法包括变换域中图像的稀疏性、图像梯度的稀疏性、正则化先验、低秩等。随着生成模型的研究发展，图像的生成式建模的进展已经远远超出传统的基于先验的算法。新的一类生成模型[22-24］被提出，它们提供了一种使用梯度数据分布对图像进行建模的强大方法，利用学习的分数函数作为先验，可以很容易地解决成像中的逆问题。近来，Song等人[22］提出使用随机微分方程（Stochastic Differential Equation，SDE）缓慢地添加噪声将复杂数据分布转换为已知的先验分布，并使用相应的反向SDE缓慢地去除噪声将先验分布转换回数据分布。至关重要的是，反向SDE仅取决于扰动数据分布的时间相关梯度场[25］，也称为分数函数。为方便表述，本文将基于分数的SDE称为基于分数匹配的生成模型。

2.2 基于分数匹配生成模型的无透镜成像方法

如图2所示，生成模型可以简单地概括为用概率分布方式描述图像的生成，通过对概率分布采样产生数据。图2右边是一个训练数据集，里面所有的数据都是从某个数据pdata中独立同分布取出的随机样本。左边是其生成模型（即概率分布），在这种概率分布中，找出一个分布pθ使得它离pdata的距离最近。接着在pθ上采新的样本，可以获得源源不断的新数据。通常，使用分数函数（概率密度函数对数的导数）来表示概率分布，称为分数匹配的生成模型。相比概率密度函数模型，它没有归一化的要求，因而模型选择更加灵活。

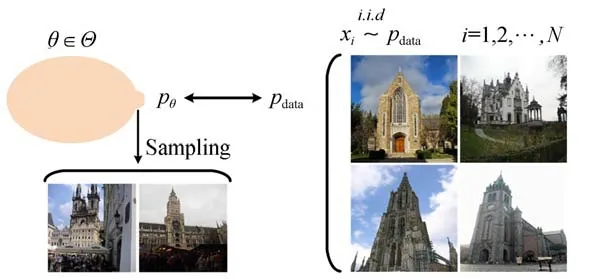
图2 生成模型Fig.2 Generative model

基于分数匹配的生成模型是一种通过优化以θ参数化的分数网络Sθ(x)来估计数据分布的分数函数的方法。用多个噪声尺度对数据进行扰动是分数匹配生成模型方法成功的关键。它定义了一个正向扩散过程（即SDE），用于将数据转换为噪声并通过其逆向过程从噪声中生成数据。如图3所示，分数模型使用一个正向SDE通过添加高斯噪声扰动数据分布，为了从数据分布中进行采样，可以训练一个神经网络来估计对数数据分布的梯度（即∇xlog pt(x)），并用它来数值求解逆时间SDE从噪声中生成数据。

本文通过使用分数模型对目标图像数据集进行训练，将学习到的图像先验信息引入无透镜成像逆问题，然后通过预测-校正采样算法以实现高质量的无透镜成像重建。

具体来说，训练阶段，通过将目标图像数据集输入基于分数匹配生成模型进行训练。该模型使用SDE通过缓慢添加高斯噪声扰动数据分布，然后使用方差爆炸（Variance Exploding，VE）-SDE的去噪分数匹配方法训练了一个连续时间相关的分数函数Sθ(O)估计对数数据分布的梯度，即模型学习的梯度先验∇Olog pt(O)，其中O为目标图像数据集。测试阶段，根据训练的分数函数（即目标图像先验）和逆时间SDE数值求解器迭代更新重建目标图像。在非相干光照明下由单张FZA调制的编码图像，通过训练好的分数网络先经过数值求解器SDE一次预测，再通过退火朗之万方法在数值求解器SDE和数据保真项步骤之间轮换更新以实现编码图像的重建。基于分数匹配生成模型的无透镜成像方法的训练和重建算法将分别在2.3和2.4节展开介绍。

图3 SDE的正向和反向过程Fig.3 Forward and reverse time process of SDE

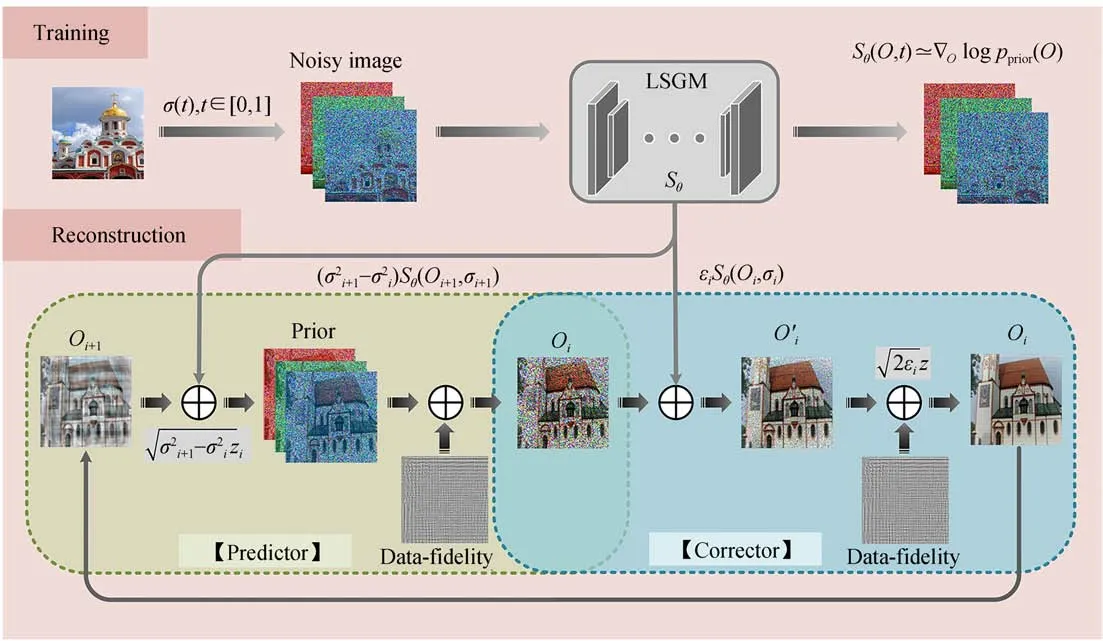
图4 LSGM算法的训练与重建流程图Fig.4 Training and reconstruction flow chart of LSGM algorithm

2.3 基于分数匹配生成模型的训练

图4为LSGM算法的训练与重建流程图。本论文提出的LSGM方法的训练过程如图4上半部分所示。首先，模型构造了一个连续扩散过程其中，O(t)∈RNxy，t∈[0，T]是时间变量。正向过程是将数据分布O(0)通过随机过程扰动得到含噪图像O(T)。其中，O(0)～pdata，pdata表示目标图像数据分布；O(T)～pT，pT表示先验数据分布。那么，该随机过程可以建模为求解以下SDE过程：

其中：f∈RNxy和g∈R分别是漂移系数和扩散系数，w∈RNxy是标准维纳过程或称布朗运动。

然后，通过求解逆时间SDE来重建编码图像。具体而言，从正向SDE训练过程学习的目标相关的先验信息O(T)～pT开始求解式（6）的逆向问题可以得到O(0)～pdata目标图像，其中pT是一个包含pdata信息的非结构化先验分布。那么，逆SDE过程为：

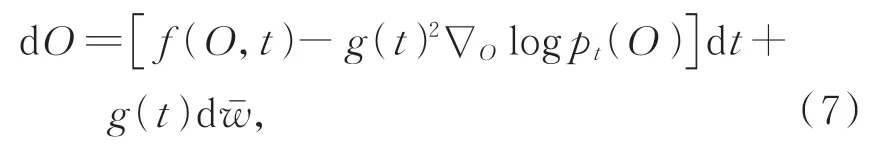
为了求解公式（7），需要已知所有t的分数函数∇Olog pt(O(t))。通过训练一个基于时间的评分网络Sθ来匹配Sθ(O，t)≃∇Olog pt(O(t))[26］，然后将这个网络函数替换式（7）中相应项。因此，通过对分数网络的参数θ进行优化：

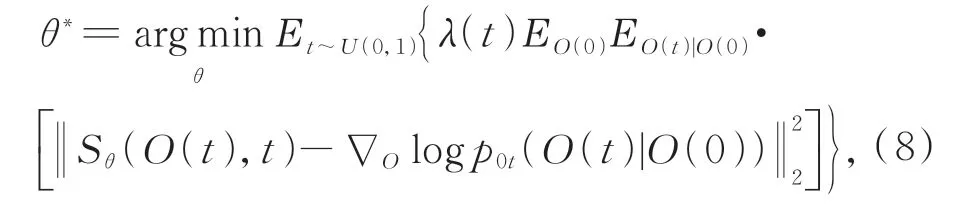
其中：E表示期 望，λ：[0，T]→R＞0为正 权重函数，t在[0，T]上均匀采样，p0t(O(t)|O(0))是以O(0)为中心的高斯扰动核，∇Olog p0t(O(t)|O(0))表示扰动核的梯度，σ(t)是噪声尺度的单调递增函数。通过公式（8）训练的网络模型应当满足Sθ(O，t)≃∇Olog pt(O(t))， 这 意 味 着∇Olog pt(O)对所有t都被训练的Sθ(O，t)所知。因此，可以将其带入逆时间SDE求解公式（7）并对其进行模拟以进行采样。

2.4 基于分数匹配生成模型的重建

无透镜成像问题归结为求解方程（5），求解该逆问题的经典方法是转化为优化以下约束问题：

其中：Ψ是正则化项，τ是正则化系数。在求解上式时，通常使用变量分裂[27］或投影到凸集[28］等近似算法将先验信息项和数据保项优化解耦，然后根据轮换求解思路在两个子问题之间交替更新实现最优解：

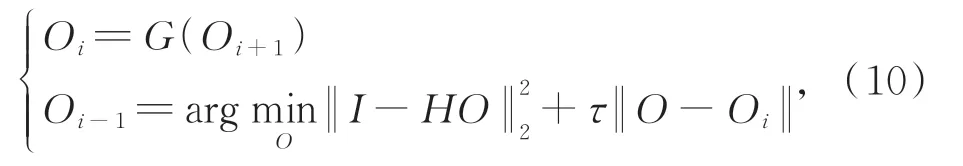
其中，第一个公式为生成；第二个公式的第一项是数据保真项，第二项是正则化项，τ是正则化系数。

根据贝叶斯最大后验估计，如果生成模型能够准确地从目标图像数据集中估计复杂先验数据分布，可以实现高质量的无透镜成像重建。在2.3节中，详细阐述了基于分数匹配生成模型的先验学习过程。在上述训练过程中，一旦训练好分数网络Sθ(O，t)，并将其带入公式（7）中，即可以求解逆时间VE-SDE，实现无透镜编码图像重建：

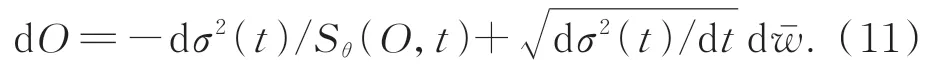
对于该过程的求解，可以使用欧拉离散化[22］求解VE-SDE的数值。为了校正离散化方向SDE演化中的错误，根据预测-校正的思想引入了一个预测-校正采样器（Predictor-Corrector，PC）。基于分数匹配生成模型先通过数值求解逆时间VE-SDE从得到的目标图像的先验分布中获得初步预测的重建图像，然后通过使用退火朗之万[29］作为校正器来校正这个初步预测结果。与此同时，在求解逆时间VE-SDE和退火朗之万采样时，每个无条件采样更新步骤之后都需要进行一次保真。基于无透镜成像的迭代重建算法如下：

预测：该预测器可以是逆时间VE-SDE的任意数值解算器，并具有固定的离散化策略。从目标图像先验分布中生成目标图像可以通过求解由式（11）得到：

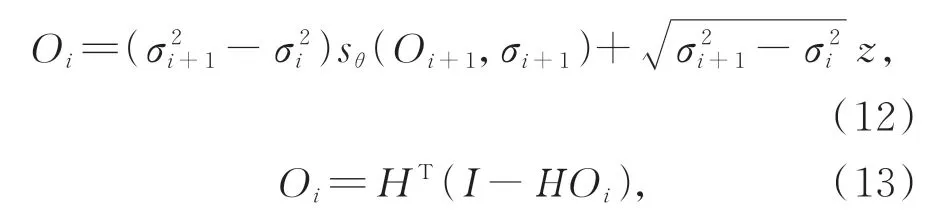
其中：σi噪声尺度，i是总迭代次数，z是零均值的高斯白噪声。式（13）称为数据保真步骤，可以有效增强数据的一致性。式（12）和（13）即为该算法的预测过程。

校正：本文使用朗之万马可夫链[29］校正算法校正梯度上升方向，得到校正器步骤：

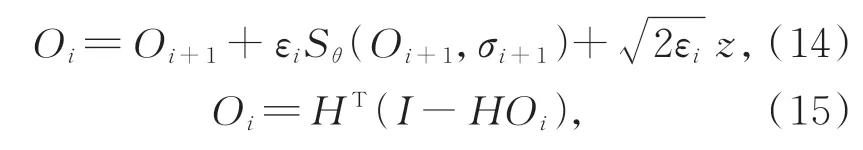
其中，εi是第i次迭代的步长。式（14）和（15）称该算法的校正过程。

本文最终产生的LSGM的重建算法的伪代码如算法1所示。LSGM重建过程包含两层循环：（1）外层循环次数为逆时间VE-SDE的离散化步骤数，无透镜编码图像输入网络先进行一次预测，再进入内层循环校正；（2）内层循环的校正过程是通过退火朗之万迭代1 000次。整个循环迭代过程中，每一次循环均对预测和校正过程的数据先验项和数据保真项进行更新，经过1 000次的迭代实现无透镜成像重建。

图4下半部分展示了本文提出的LSGM算法的重建流程图。在训练过程，利用生成模型对随机样本训练估计数据分布的梯度先验；在重建过程，先利用训练的梯度先验进行一次预测，然后再利用退火朗之万方法迭代进行校正，并且在每一次迭代完成，都会在预测和校正步骤之后对数据保真项和先验项进行更新，以保证实现最优求解。

Algorithm 1 LSGM Training Dataset：Object image dataset Output：Sθ(O，t)≃∇O log pt(O)Reconstruction Setting：Score network Sθ，Noise iteration step{εi}，Noise scale{σi}，Number of discretization steps for the reverse-time SDE N，Number of corrector steps M 1：ON～N(0，σ2max I)2：For i=N-1 to 0 do（Outer loop）3：Update Oi via Eq.（12）and（13） 【Predictor】4：For j=1 to M do（Inner loop）5： Update Oi via Eq.（14）and（15）【Corrector】6：End for 7：End for 8：Return O0

3 实验结果及分析

在本章节中，接下来的实验将从定性和定量两方面对本文提出的方法进行评估。

3.1 数据集和模型训练

由于目前还没有用于无透镜编码成像的公共数据集，本实验所做的训练和测试均在LSUN数据集上进行。LSUN数据集是一个大型的彩色图像数据集，包含10个场景类别和20个对象类别，每个类别包含约100万幅标记图像。主要选取其中两个子数据集：室内场景LSUN-bedroom和教堂LSUN-church数据集，分别观察网络模型在两不同训练集上的训练和测试效果。

具体地说，使用LSUN官方网站给出的用于训练的bedroom和church数据集分别训练，图像设置大小为256×256，其像素值均缩放至[0，1]之间。使用噪声数值范围为0.01～380的高斯噪声扰动数据分布。同时，为规避数值问题，参数设置ε=10-5，信噪比为0.16。将梯度裁剪的最大值设为1.0，参数采用指数移动平均，流速为0.999，每种数据集训练50万次。此外，为了进一步验证LSGM网络的性能表现，在每个数据集中选取100张图做测试。在PC采样算法重建中的内外层循环迭代次数分别为N=1 000、M=1，每张图迭代1 000次，取最大的峰值信噪比及其相应的结构相似性值，然后对这100对数据取平均。基于仿真实验使用固定学习率0.000 01，优化采用自适应估计方法（Adaptive Moment Estimation，Adam），其中β1=0.9，β2=0.999。

3.2 评价方法

由于人眼的视觉特性，经常出现评价结果与人的主观感觉不一致的情况。为有效定量评价本文的实验，主要使用以下几个指标来评估重建质量：

峰值信噪比（Peak Signal to Noise Ratio，PSNR，IPSNR）是基于对应像素点间的误差，单位为dB。该指标是基于误差敏感的图像质量评价，数值越大表示失真越小。它是使用最为广泛的一种图像客观评价指标，定义如下：

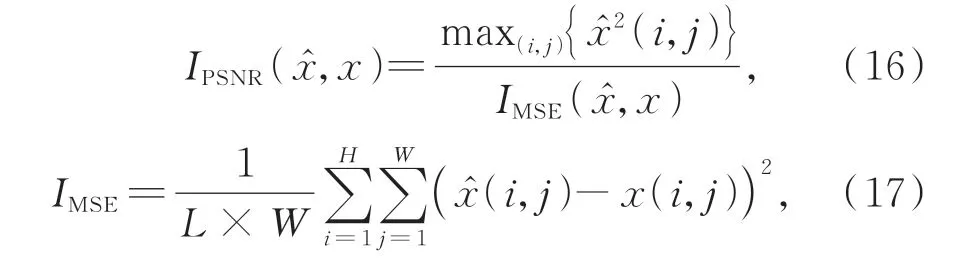
结构相似性（Structural SIMilarity，SSIM，ISSIM）：是一种衡量两幅图像结构上相似程度的指标，它分别从宽度、对比度、结构三方面度量图像之间的相似性：

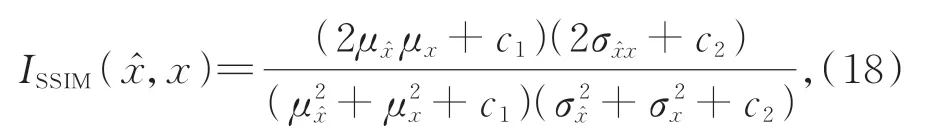
其中：μ和μx分别表示目标图像和重建图像的均值，σ和σx分别表示目标图像和重建图像的方差，σ表示图像的协方差，c1和c2是用于保持稳定的常数。结构相似性的取值范围是[0，1]，其值越大，表示图像失真越小，越能被人眼所接受。

3.3 实验设置及环境

本实验的模拟仿真实验参数设置具体如下：FZA作为编码掩膜放置在图像传感器3 mm处，目标大小为15 mm×15 mm，置于距离编码掩膜20 mm处，掩膜板最内侧区域半径r1=0.23 mm。模拟传感器的像素数为256×256，像素间距为0.014μm。传感器上每个像素探测器记录的是编码掩膜上多个孔径所成图像的一个叠加，即来自场景中多个位置入射光场的叠加。

软件仿真环境为：实验使用基于PyTorch的深度学习框架，在一张2080 TI的GPU上进行LSGM算法的训练和测试。为了更好地体现算法的可重复性，我们将代码公开在网址：https：//github.com/yqx7150/LSGM.

图5 LSUN-bedroom数据集上重建图像的视觉比较Fig.5 Visual comparison of reconstruction images on the LSUN-bedroom dataset

3.4 实验结果

3.4.1 LSUN-bedroom数据集上的实验结果及分析

近年来，随着数据量的急剧增长和计算能力的不断提高，基于分数匹配生成模型的成像方法已经被应用于磁共振成像[30］和CT成像重建[31］，然而尚未应用于无透镜成像。为证明本实验的有效性，本实验挑选了传统的BP算法和目前实验结果较好的CS算法[16］作为对比算法。

为从视觉上比较，图5从LSUN-bedroom数据集中挑选出四组不同实验结果进行展示，其中每组实验结果包含原图、编码图和BP、CS、LSGM算法重建的图。可以很直观地看出，BP算法实验结果最差，可以观察到很明显的孪生像效应。其次，CS算法的重建结果与原图对比，存在明显的颜色差异，而且其图片清晰度存在很大差距。例如，在第二行和第三行中CS重建结果与原始图像有很明显的颜色差距，中间有很明显的颜色扩散以及图片边缘黑色区域变色现象。显然，图5中第五列的图像质量明显优于另外两组结果，三种算法中LSGM的重建结果最优。

为进一步进行定量分析，三个算法的平均PSNR和SSIM值如表1所示。从表中分析可知，传统的BP算法的平均PSNR值仅为7.78 dB。相比之下，其余两种算法通过迭代的方式可以获得更好的结果。对比表中数据，CS和LSGM的PSNR值分别比BP算法高10.69 dB、18.32 dB。本文提出的LSGM算法具有最优的成像质量，在迭代校正之后，其PSNR值 为26.10 dB、SSIM值 能 达 到0.64，比CS算法 的PSNR和SSIM分 别 高 出7.63 dB和0.33。

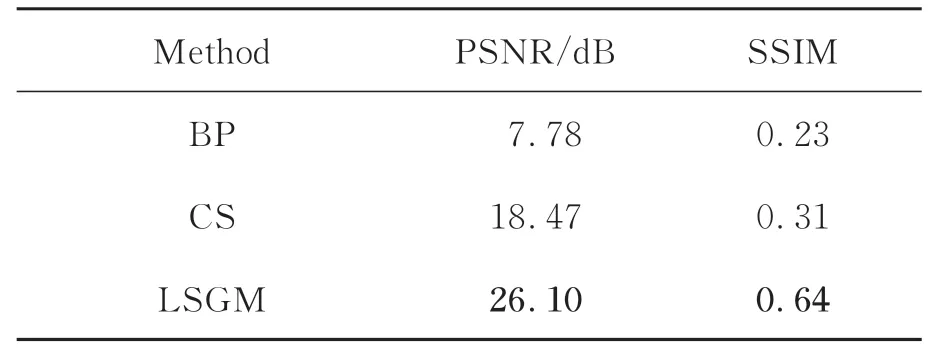
表1 LSUN-bedroom数据集上测试结果Tab.1 Test results on LSUN-bedroom dataset

3.4.2 LSUN-church数据集上的实验结果及分析

为了更好地验证LSGM方法的鲁棒性，本实验还选取了另一个图像灰度、亮度和结构变化更丰富的LSUN-church（256×256）数据集进行实验。在使用LSUN-church数据集对LSGM模型训练完成之后，选取其中100张图像作为测试输入。

图6展示了BP、CS和本文所提出的LSGM三种算法在LSUN-church数据集上重建图像的视觉比较。和上小节实验相同，本实验展示了四组不同的重建图像，每组包含原图、编码图和BP、CS、LSGM算法重建结果。与在LSUN-bedroom数据集上的实验结果相似，BP算法重建结果最差；CS算法重建的图像上总是会有与图片不相关的颜色出现。例如，图6中第一、二和四行的CS重建结果中能观察到明显的紫色和绿色孪生像，尤其是图片中间区域和边缘黑色区域更为明显。虽然CS算法重建结果并不影响图像的辨识，但图像质量仍然较模糊。对比图6中第三行的CS和LSGM算法重建结果，可发现LSGM算法具有更高的清晰度。根据图6中给出对应的PSNR和SSIM，LSGM算法重建的定量评价指标也是最高的，LSGM的PSNR和SSIM比CS算法分别提高6.68 dB和0.36。整体对比图6中各组重建结果，最后一列图像不论在图像颜色、亮度和清晰度上都优于第三列和第四列。因此，LSGM算法是表现最好的，它在保证颜色的同时，还能清晰地重建出图像细节，更加接近原始图像。

定量对比表2中PSNR和SSIM两项指标数据，在 三 个 算 法 中，LSGM的PSNR和SSIM值最高，在该实验数据集上的平均PSNR值接近于LSUN-bedroom数据集上的结果。在更换成一个灰度、亮度和结构变化更为丰富的数据集后，BP算法重建记录的评价指标几乎不变。CS算法的PSNR值下降了0.68 dB，而SSIM值下降0.02。整体分析，本文提出的LSGM基算法在两项指标上均表现得相对稳定且最好，PSNR值最高达到24.47 dB、SSIM值达到0.65。相对BP和CS算法，LSGM算法的平均PSNR值依旧分别提高16.66 dB和6.68 dB，平均SSIM值分别提高0.43和0.36。因此，本文提出的方法重建图像最好，不仅能够在保持颜色、亮度和清晰度的同时，还能显著去除孪生像的伪影噪声。

综合上述两组实验结果可以得出结论，在不同数据集上，与BP算法、CS算法相比，LSGM方法都能达到更高的重建质量，模型性能更加稳定。

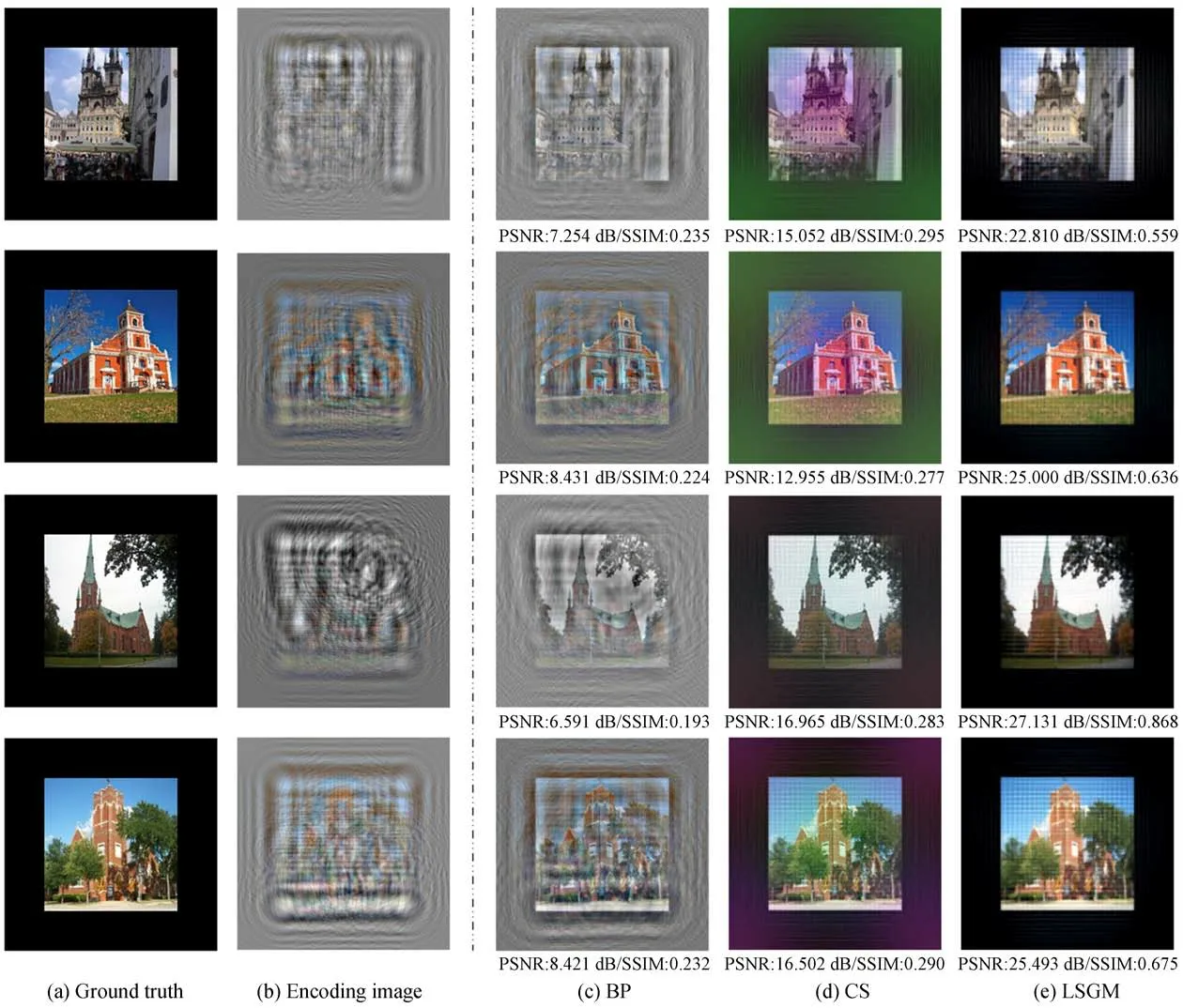
图6 LSUN-church数据集上重建图像的视觉比较Fig.6 Visual comparison of reconstruction images on the LSUN-church dataset

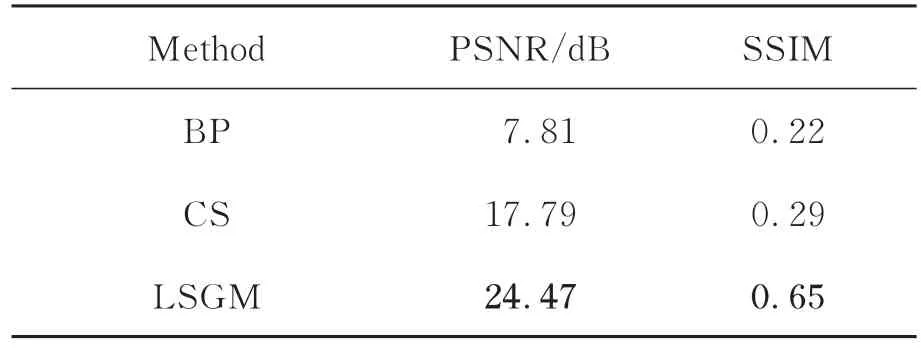
表2 LSUN-church数据集测试结果Tab.2 Test results on LSUN-church dataset

3.4.3 TV去网格效应

由于无透镜成像本身特性，重建图像存在很明显的“网格”现象，重建图像和原始图像存在一定差距，在图像纹理细节部分的恢复结果仍然不够理想。为了解决这个问题，本文将基于变分理论的TV方法应用于重建过程。该方法是依靠梯度下降流对图像进行平滑，希望在图像内部尽可能对图像进行平滑（相邻像素的差值较小），而在图像边缘（图像轮廓）尽可能不去平滑。前两个实验证明了本文提出的LSGM模型生成的先验信息作为正则化项求解无透镜成像逆问题，并取得了较好的数值结果。图7展示了使用及不使用TV方法的LSGM算法的重建结果以及原始图像。从图7（c）可以看出，结合了TV方法的重建图像中“网格”效应更为平滑，视觉效果更令人舒适，但其相应代价是失去了图像中的部分高频信息。由两种方法重建结果的定量指标可以得出，提出的LSGM算法比不使用TV方法的LSGM算法的PSNR和SSIM值分别平均提高0.80 dB和0.10。

图7 使用TV方法的LSGM算法对视觉效果的提升Fig.7 Improvement of visual effects by LSGM algorithm with TV method

4 讨 论

4.1 消融实验

上述实验表明，本文提出的LSGM方法能够实现高质量的无透镜成像结果。然而，使用基于分数匹配生成模型进行图像重建时，迭代式重建方法在耗时方面有着明显的局限性。为了更好地验证LSGM模型的性能，本实验探究了在不同σmax下的图像质量和离散化步骤数之间的关系。

如图8所示，本实验选取了LSUN-church数据集对测试需要的离散化步骤数与图像质量之间的关系进行实验验证。当训练阶段使用N=1 000个离散化步骤来进行正向SDE，重建阶段使用N=1 000个离散化步骤时，需要大约10 min的推理时间。从N=1到N=1 000每隔1个离散化步骤记录重建图像的PSNR以及SSIM。可以观察到随着离散化步骤的增加，重建图像PSNR以及SSIM呈现一定的规律性。在N=700的情况下，可以实现高质量的重建图像，PSNR以及SSIM达到最高值。当离散化步骤数逐渐增加，PSNR值趋于稳定，SSIM会下降。由于在不同σmax下，PSNR随着离散步骤数增加，将趋向于稳定，并且稳定值在24 dB左右，而SSIM波动较大，所以本文选取当PSNR达到稳定值下的离散步骤数来进行所有实验。在之后的工作中，我们将尝试使用去噪扩散模型（DDPM）[32］来进一步减少离散化步骤数。

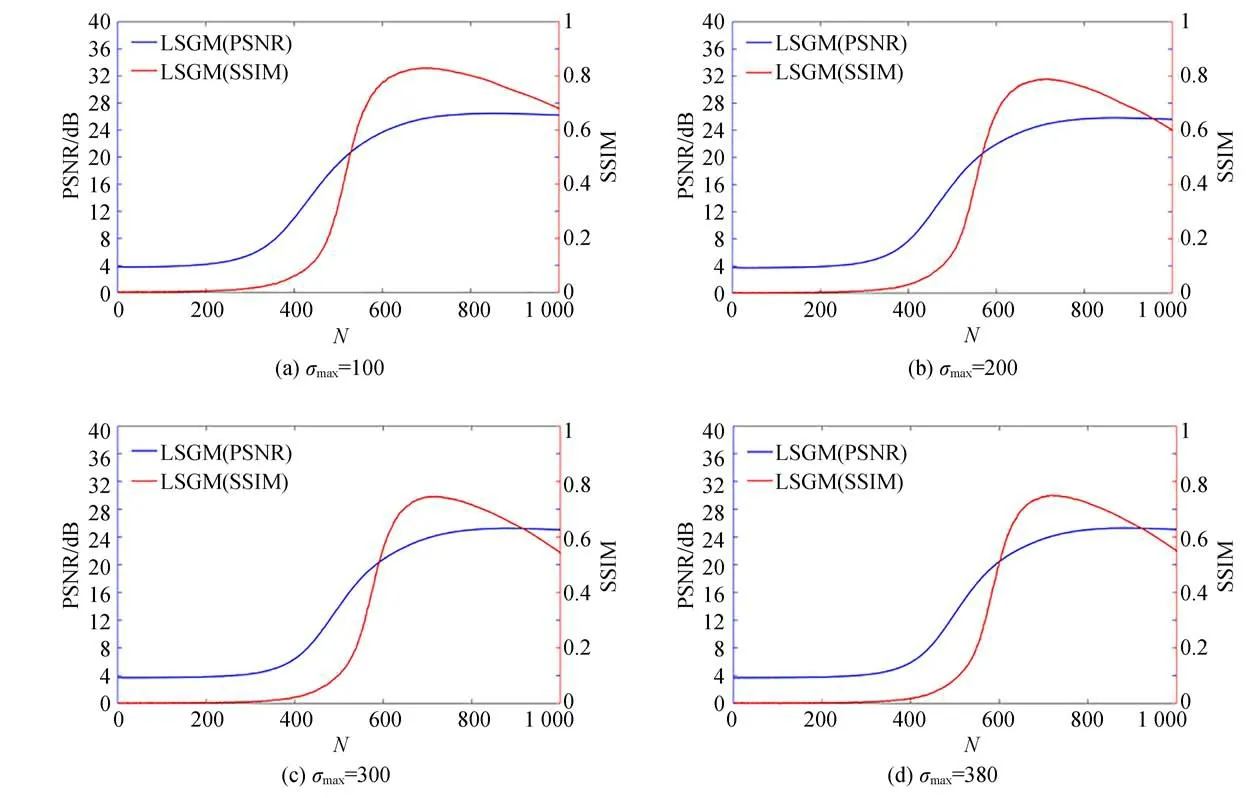
图8 不同σmax下的图像质量和离散化步骤数关系的消融实验Fig.8 Ablation experiments on the relationship between image quality and discretization steps under differentσmax

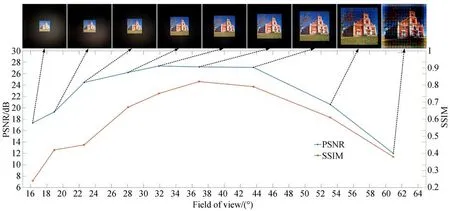
图9 视场角测试实验Fig.9 Experimental test of field of view

4.2 成像视场分析

如图9所示，为测试视场角对本文提出算法的影响，进一步分析了不同视场角下重建图像的PSNR和SSIM指 标。在 本 组 实 验 中，FZA的 参数与前文一致，在保持目标尺寸不变的情况下，通过改变目标物与FZA掩膜间的距离来实现不同视场角。从图9所示结果可以看出，随着视场角的增大，PSNR的值先增大后减小，随着目标图像的增大，边界处部分衍射信息丢失，造成图像重建质量的恶化。当视场角在32°～46°范围内，相应的PSNR的值可达到26～28 dB、SSIM的值为0.85～0.68，可以实现最好的成像效果。

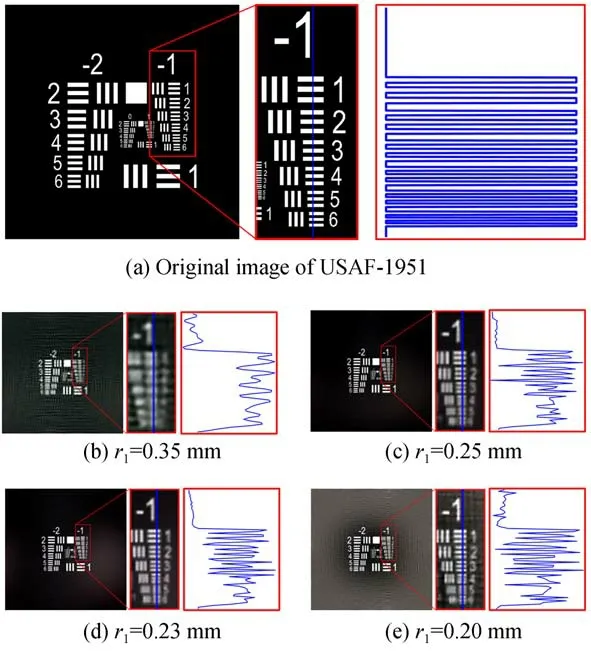
图10 分辨率测试实验Fig.10 Experimental test of the resolution

4.3 成像分辨率分析

受制于工艺制造水平，传感器和FZA掩膜的像元尺寸不能无限小，系统重建的带宽有限。为了验证提出算法能实现的最小分辨率，本文采用一张尺寸为20 cm×20 cm、像素数为1 280×1 280的USAF-1951测试图像进行测试，该成像目标与FZA距离为267 mm，成像视场角为41.11°。由于本文训练模型中传感器的像素数为256×256，为了适应本文算法，将USAF-1951原图经过FZA调制后的结果进行像素归并至像素数为256×256，以得到测量结果。

图 像 重 建 结 果 如 图10所 示，图10（a）为USAF-1951测试卡原图、-1组线对的细节以及相应的剖线。为了测试不同FZA参数r1对结果 的 影 响，本 文 在r1分 别 为0.35、0.25、0.23、0.20 mm时进行了重建。可以很明显看出，r1=0.35 mm时，难以分辨-1组线对。随着r1参数的减少，图像分辨率得到有效提高，当r1减小到0.23 mm及0.20 mm时，能够有效分辨出-1组4号 线 对。

5 结 论

本文提出了一种基于分数匹配生成模型框架的无透镜成像方法，即LSGM。该模型利用数据分布梯度对图像进行建模，并从给定的观测数据的条件分布中采样数据，然后将采样的数据作为图像先验数据用于图像重建。所提出的LSGM算法在计算重建过程中能够有效消除无透镜成像系统固有的病态性而带来的孪生像伪影噪声及其他影响成像的不良影响，使得成像质量大幅提高。在LSUN-bedroom和LSUNchurch数据集上测试结果表明，本文提出的方法和其他传统算法相比，LSGM算法图像重建的平均PSNR值和平均SSIM值分别达到25.23 dB和0.65，量化指标以及视觉质量均获得了令人满意的结果。本文提出的模型框架结构灵活，训练稳定，在建模数据分布方面的性能表现出色，能够获得高质量样本。本文通过大量的实验验证了该方法在质量和实用性方面的优越性，有望应用于其他计算成像领域。