使用改进型大气散射模型的双阶段图像修复

张楠楠，李志伟，郭新军，肖新杰，阮 昊

（1.上海工程技术大学 电子电气工程学院，上海 201620；2.中国科学院 上海光学精密机械研究所，上海 201800）

1 引 言

空气中的悬浮粒子使大气光发生散射现象，导致在该环境下采集的图像质量严重退化，从而对依赖于清晰图像的计算机视觉任务产生严重的影响[1-4］。因此，对在恶劣条件下获得的退化图像进行修复，并改善图像的质量，具有十分重要的意义。目前，图像去雾的相关研究取得了较大进展。

传统的去雾方法[5-11］中，较为典型的图像增强方法包括基于Retinex理论的方法[5］和基于直方图均衡化[6］的方法等，这类方法未考虑在恶劣条件下图像的成像原理，导致获得的去雾结果中存在过度增强和色彩失真等一系列现象。He等[7-8］利用先验推算出物理型中的未知参数，进而求得无雾图像，由于在去雾的过程中先验具有不确定的未知因素，导致去雾结果中容易存在过饱和、偏暗、色彩失真和光晕等现象。Berman等[9］假设雾线由无数种颜色簇组成并提出一种非局部先验的去雾算法，但仍存在色彩失真的问题。这些基于大气散射模型的传统去雾方法取得了长足的发展，但基于此方法得到的去雾结果中存在色彩失真和色调偏暗的问题，这是由于引入的先验知识具有不适用性，导致图像去雾过程中放大了噪声。

近年来，深度学习被研究者广泛应用于计算机视觉任务。如被应用于基于深度学习的去雾方法[12-16］，在这类去雾方法中，Li等[12］和Cai等[13］使用深度学习的方法直接估算大气散射模型中的未知参数，以用于求解无雾图像，这类方法的去雾结果存在细节丢失和色彩失真。与这两种方法不同的是，Qu等[14］的去雾方法不需要估算大气散射模型中的未知参数，而是直接采取有雾图像到无雾图像转换的策略，避免了因估算的未知参数不准确所带来的负面影响，即使如此，其去雾结果中仍存在色彩失真和色调偏暗的问题。基于深度学习的去雾方法在去雾效果上优于传统的去雾方法，但深度学习的去雾方法也存在不足，其在学习的过程中，由于数据集中所包含的特征信息与真实世界雾霾图像中的特征信息有所差异，导致从数据集中学习到的特征信息与真实世界中的雾霾图像不完全符合，造成对雾霾图像的去雾结果中存在雾残留、色彩失真和色调偏暗等问题。

综上所述，传统的去雾方法和基于深度学习的去雾方法能够在一定程度上实现雾霾图像去雾，但去雾结果中存在色调偏暗、色彩失真和光晕等问题。此外，这些方法仅能用于图像去雾，而不能实现水下图像修复和夜间图像增强。Dong等[17］指出低照度图像的表征图像和直方图表征，与雾霾图像具有很高的相似度。因此可以寻找出一种适用性较强的图像修复方法。

针对对比度下降、色调偏暗和色彩失真等问题，本文提出一种使用改进型大气散射模型的双阶段图像修复方法。实验结果可证明，所提出的方法具有很好的适用性，既可有效实现雾霾图像去雾，又能实现水下图像修复和夜间图像增强。所提出的方法不仅避免了最终的修复结果中存在色彩失真和色调偏暗的问题，而且在定量和定性实验上都取得了优异的结果。

2 物理模型

2.1 传统大气散射模型

目前被广泛应用于描述图像退化的大气散射模型[18-20］，其数学表达式为：

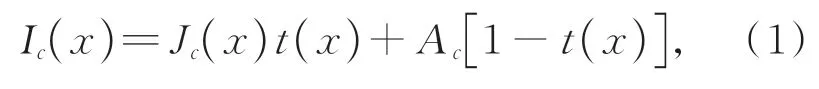
其中：x为像素点位置，c为通道索引且c∈{R，G，B}，Ic(x)为退化后的图像，Jc(x)为清晰图像，Ac为全局大气光值，t(x)为透射率。在式（1）表示的大气散射模型中，等号右边的第一项称为直接衰减项，其描述了场景目标的反射光在传播介质中的衰减过程；等号右边的第二项称为大气光项，其描述了大气光经过空气中悬浮颗粒的散射，会导致图像发生色彩失真。通过分析式（1）可知，Ic(x)是输入的已知图像，为了反推出清晰图像Jc(x)，只需求出Ac和t(x)即可实现退化图像的修复。其中，透射率t(x)在均匀介质中可表示为：

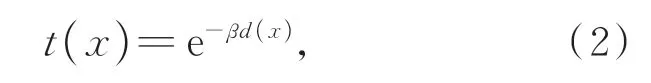
其中：β为大气散射系数，d(x)为场景深度。进一步，式（1）可表示为：

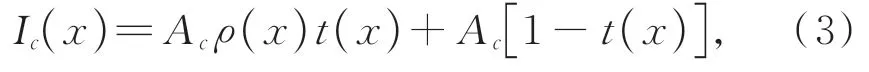
其中：ρ(x)为场景反照率，其中Acρ(x)=Jc(x)。

2.2 水下光学成像模型

水 下 光 学 成 像 模 型 由McGlamery[21］和Jaffe[22］正式提出。在Jaffe-McGlamery模型中，水下光学成像模型由三个分量组成：直接透射、背景透射和前向透射，其数学形式可以表示为：

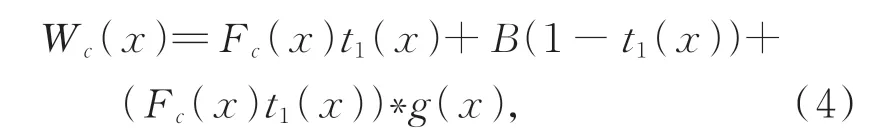
其中：x为像素点位置，c∈{R，G，B}为通道索引，Fc(x)为水下清晰图像，t1(x)为透射率，B为水下背景光，*为卷积算子，g(x)为点扩展函数。为避免通过估计点扩展函数来求解反卷积的数学不适定问题，研究者通常假设水下场景足够靠近相机，并忽略前项散射的影响[23］，因此式（4）可简单的表示为：

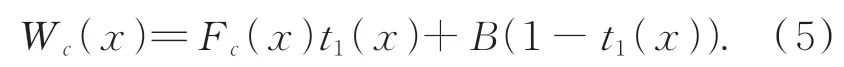
此时，可以发现式（5）和式（1）的大气散射模型表达形式相同，在文献[23］中也提到水下光学成像模型类似于大气散射模型。基于水下光学成像模型的水下图像修复方法，亦需要通过强有力的假设或先验来估计水下光学成像模型的两个未知参数：透射率t1(x)和水下背景光B。在文献[17］中提到低照度图像的表征图像和直方图表征，与雾霾图像具有很高的相似度，又因为水下退化图像和夜间模糊图像都属于低照度图像，使得设计出一种适用性较强的图像修复方法成为了可能。本文对大气散射模型进行改进，并使用该改进型大气散射模型设计了一种双阶段图像修复方法。

2.3 改进型大气散射模型

基于传统大气散射模型的传统修复方法一般是通过引入先验知识求解该模型中的两个未知参数：透射率和全局大气光值，这些方法得到的结果普遍存在对比度下降、色调偏暗以及色彩失真等问题。根本原因是虽然传统大气散射模型中入射的大气光是个常数，但大气光对不同的场景具有不同的照明效果，因为不同场景中的物体具有不同的纹理密度，而光又可以在纹理中被吸收，光吸收率会随纹理密度而发生变化，造成场景色调或明或暗和对比度下降。在文献[24］中，通过在石墨烯上引入无序的纳米纹理来实现光捕获，这在微观水平上增加了光吸收率。同样地，在宏观视图中，亦是纹理密度越高光吸收率越大。由文献[25］可知，退化图像中的场景深度越小，纹理密度越丰富，其光吸收率越大，由于基于传统大气散射模型的修复方法没有对传统的大气散射模型进行改进以避免场景中物体纹理密度对光吸收的负面影响，导致得到的修复结果对比度低且整体色调偏暗，尤其是场景深度小的区域色调最暗。传统大气散射模型的第二项称为大气光项，描述了空气中悬浮的粒子会对周围的环境光进行散射造成色彩失真，且色彩失真程度与场景深度相关[26］。因此，为解决对比度下降、色调偏暗以及色彩失真等负面问题，本文首先改进传统的大气散射模型，在传统大气散射模型中引入一个全局补偿系数u(x)来削弱场景中物体的纹理密度对光吸收率的影响以及空气中悬浮的粒子会对周围的环境光进行散射造成色彩失真的影响。改进后的大气散射模型可以用数学形式表示为：

根据文献[26］可知，场景深度的变化会对修复结果产生不同程度的影响。场景深度越大修复结果中越容易存在色彩失真以及色调偏暗等问题，为避免这种影响，根据实验经验，引入一个小于1的全局补偿系数u(x)，其数学表达形式为：

通过联立式（2）、（6）和（7）可得到本文所提出的改进型大气散射模型的数学表达为：

该改进型模型是基于传统大气散射模型进行改进的，因此根据文献[23］可知，该改进型大气散射模型同样与水下光学成像模型极为相似。根据文献[17］可知，水下图像和夜间图像的表征图像及直方图表征与雾霾图像具有很高的相似度，所以该改进型大气散射模型亦可用于水下图像和夜间图像的修复。因此，可提出一种适用性较好的图像修复方法，通过大量实验证明，其既可应用于雾霾天气又可应用于水下，甚至黑夜，同时可以避免修复结果中存在对比度下降、色调偏暗和色彩失真等问题。

3 使用改进型大气散射模型的双阶段图像修复方法

前面的工作已经得到改进型大气散射模型如式（8）所示。进一步分析式（8）可知：Ic(x)是已知的退化图像，Ac则可以通过四叉树法[27］求得，根据文献[28］ρ(x)近似取值为0.5。此时，公式（8）中还存在两个未知参数t(x)和tmin。不难发现，式（8）中存在对数函数，为了简化对t(x)和tmin的求解，根据文献[28］对其进行拟合分析得到：

其 中：z1=-0.397，z2=0.07747时，对 数 函 数与有理函数的拟合程度最好。通过联立式（8）和（9）可得到简化后的数学表示形式为：

在式（10）中，若将tmin看作一个常数，则式（8）是一个关于t(x)的一元二次方程。因此，只需要求出tmin就可轻而易举地求得透射率t(x)。为便于求解tmin，结合黄金分割法设计一个求取tmin的全局搜索方法（Global Search，GS，fGS），该方法可通过数学形式表示为：

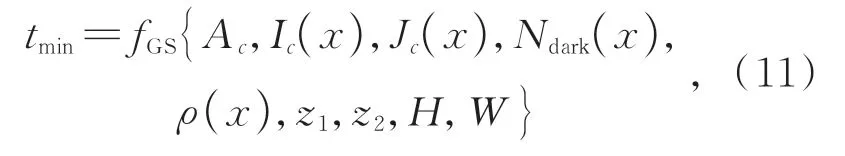
其中：H和W表示图像的尺寸大小，Ndark(x)=且Ω(x)是以像素点x为中心的局部块。tmin通过该方法求得后，便可求得透射率t(x)，为使图像过度的比较平滑同时保持图像的边缘信息，受文献[29］和[30］启发，本文使用引导滤波[8］进一步细化透射率并得到最终的透射率t(x)。

通过联立式（3）、（8）和（9）可得到清晰图像Jc(x)的数学表达形式为：

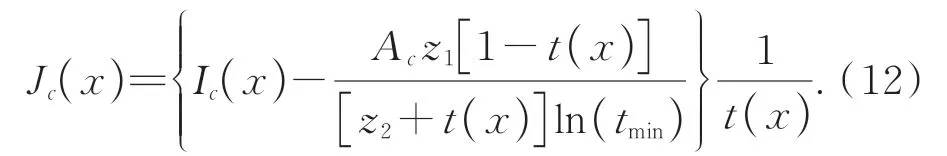
在前面的描述中，式中未知量Ac，ρ(x)，t(x)和tmin均可被求出，由此，在使用改进型大气散射模型的双阶段图像修复中，利用式（12）便可得到修复后的清晰图像Jc(x)。所提出的使用改进型大气散射模型的双阶段图像修复流程图如图1所示，图像修复具体包含两个阶段。

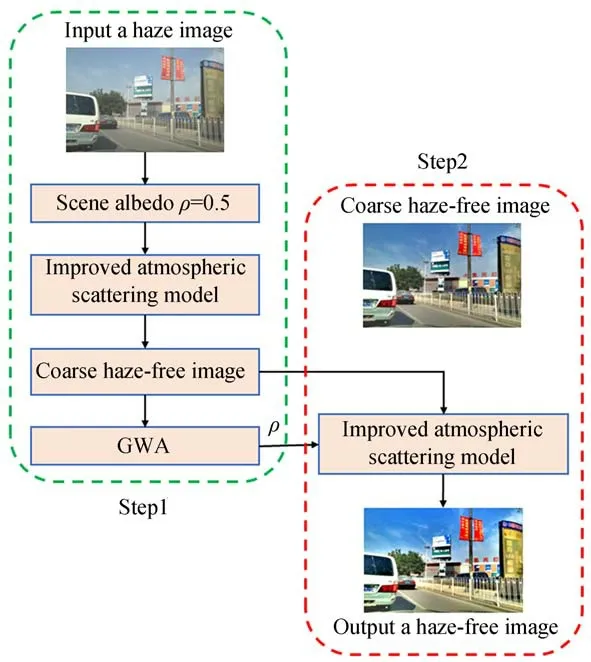
图1 双阶段图像修复流程图Fig.1 Flowchart of two-stage image restoration

首先，需要输入一张退化图像，然后利用式（12）求得粗略的清晰图像，因为在前面的处理中，为方便求取全局大气光值和透射率，根据前人的经验，反照率取值为0.5，但该取值并不适用于所有的场景，导致在部分场景下的修复结果会发生色彩失真。为了保证使用改进型大气散射模型的双阶段修复方法具有较强的适用性，既能处理雾霾图像，又能处理水下图像和夜间图像，利用灰度世界算法，求出一个较为合理的反照率，本文只需要根据灰度世界算法，便可求出该粗略的清晰图像的反照率。根据灰度世界算法[31］可知，我们需要先求出每个通道的平均值，然后求出每个通道的增益系数，并根据增益系数调整每个通道的分量，最后得到合理的反照率ρ(x)。由式（1）和式（3）可知Acρ(x)=Jc(x)，那么粗略图像对应反照率的数学形式为：

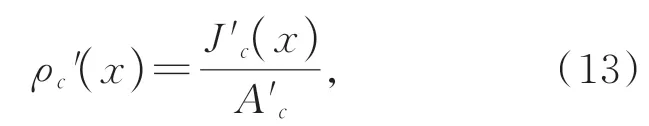
其中，c∈{R，G，B}为通道索引，那么粗略清晰图像的平均反照率可以表示为

此时，可以得到粗略清晰图像的合理反照率ρ(x)为：

因为灰度世界算法可以从图像中消除环境光的影响，所以利用灰度世界算法求得的合理的反照率ρ(x)进一步为避免修复结果中存在色彩失真提供了保证，同时保证了所提出的改进型大气散射模型的双阶段修复方法具有较强的适用性，既能处理雾霾图像，又能处理水下图像和夜间图像。

其次，将求取的合理反照率ρ(x)代入式（3）、（6）、（8）和（9）中更新参数，并将求取的四个新参数代入到式（12）中，最后该粗略的清晰图像可通过公式（12）得到最终的清晰图像。

为验证本文方法求取的合理反照率和传统方法的不同，此处进行了对比。通过式（13）可求出各方法的反照率和标准的反照率，为公平起见，在求取反照率时，统一使用RESIDE[32］数据集提供的标准大气光值Ac(x)，同时为方便实验结果对比，反照率取三个通道的平均值。为证明求取合理反照率的重要性，以及本文方法与传统方法的不同，在RESIDE[32］数据集中随机挑选3张退化图像与传统方法进行实验对比，实验结果如 图2所 示。He等[7］方 法 采 用 的 暗 通 道 先 验 知识不具有普遍适用性，并未对传统的大气散射模型进行改进，使得其反照率与标准反照率差别较大，导致得到的修复结果存在对比度下降、色彩失真和色调偏暗等问题（如图2（b）所示）。Ju等[28］方法在图像修复的过程中反照率取常数0.5，因为不同的场景具有不同的反照率，因此其将反照率取为0.5是不合适的，且与标准反照率差别较大，造成修复的结果存在色彩失真和场景过亮等问题（如图2（c）和图2（e）所示）。从图2（d）和图2（e）中可以看出，所提出方法得到的反照率与标准反照率最为接近，此时得到的峰值信噪比（Peak Signal to Noise Ratio，PSNR）和结构相似性（Structural Similarity，SSIM）值也是最高的，说明所提出的方法得到的修复结果质量最好。因此，可以得出结论：图像修复时所求取的反照率与标准反照率越接近，得到的修复结果与标准清晰图像就越接近，同时也证明，所提出的方法得到反照率较合理，修复结果也优于传统的方法。

在后面的实验中也发现，所提出的图像修复方法确实具有很好的适用性，既能处理雾霾图像，又能处理水下图像和夜间图像，并且避免了去雾结果中存在色彩失真和整体色调偏暗，使水下图像修复的结果更符合人们眼睛看到的真实场景，而且夜间图像增强后能够呈现更多的细节信息并能实现更好的视觉效果。

图2 在RESIDE数据集上不同算法的去雾结果Fig.2 Dehazing results of different algorithms on the RESIDE dataset

4 实验结果与分析

为证明所提出的图像修复方法具有很好的适用性，并且能表现出优异的性能，分别在雾霾、水下和夜间环境下开展了的实验。在雾霾图像去 雾 的 实 验 中，以DCP[7］、AOD-Net[12］、DehazeNet[13］、EPDN[14］和IDE[28］作为对比。使用的合成数据集是RESIDE[32］及其中的SOTS数据集，真实雾霾图像数据集是O-HAZE[33］数据集和IHAZE[34］数据集。在水下图像修复的实验中，对比的四种方法包括DCP[7］、Fusion-based[35］、Retinex-based[36］和Red Channel[37］，使 用 的 数 据 集 是UIEB[38］数据集。在夜间图像增强的实验中，使用的数据均来自于互联网收集的图像。实验中采用PSNR和SSIM用于评价图像修复质量的好坏，这两个指标的数值越大，表明图像修复的质量越好。以上实验均在HP笔记本电脑上进行，电 脑 配 置 为：处 理 器Intel（R）Core（TM）i5-6300HQ CPU@2.30 GHz和8 G的RAM。

4.1 合成雾霾图像的实验结果

为验证所提出方法的有效性，实验中随机从SOTS数据集选择部分合成雾霾图像，与当前典型的五种方法对比的实验结果如图3所示。He等[7］和Li等[12］的去雾方法虽然能够实现雾霾图像去雾，但这两种方法的结果中存在图像整体色调偏暗和对比度低的问题（如图3（b）和（c）所示）。与上述两种方法相比，即使Ju等[28］的方法避免了去雾图像整体色调偏暗的问题，但其仍存在场景过亮和雾残留的问题（如图3（f）所示）。通过对比可发现，Cai等[13］的去雾方法得到的去雾结果普 遍 优 于He等[7］、Li等[12］和Qu等[14］的 方法，这得益于Cai等[13］的方法采取了基于深度学习的方法，但由于其学习到的雾霾图像的特征信息与真实世界的雾霾图像有所差异，导致去雾结果中存在雾残留（如图3（d）所示）。Qu等[14］的去雾方法得到的去雾结果中存在色彩失真和整体色调偏暗的问题（如图3（e）所示）。通过与当前典型的五种去雾算法的对比实验可证明，所提出的方法得到的去雾图像不仅避免了图像整体色调偏暗，也避免了色彩失真和雾残留等负面影响（如图3（g）所示）。

为清晰展示所提出方法的优越性，与当前典型的五种去雾算法对比的客观评价指标如表1和表2所示，最优指标加粗显示。其中表1展示了在图3中使用不同去雾方法所得到的去雾图像的性能指标，表2展示了在SOTS数据集上使用不同去雾方法所得到去雾图像的性能指标的平均值。从表1可以看出，所提出的方法对SOTS数据集中随机选择的雾霾图像去雾后，所取得的PSNR值和SSIM值均为最高的，图3中的M1图像所取得的PSNR值和SSIM值分别比排名第二的高10.044 1 dB和0.049，且本文算法在其他图像上所取得的PSNR值和SSIM值也远远高于当前典型的五种去雾算法的去雾结果所取得的PSNR值和SSIM值。通过定量对比实验可得出，所提出的方法对随机选择的雾霾图像进行去雾仍具有优越性。

图3 在SOTS数据集上不同算法的去雾结果Fig.3 Dehazing results of different algorithms on the SOTS dataset

表1 图3相对应的各去雾算法去雾结果的性能指标Tab.1 Performance metrics of dehazing results of various dehazing algorithms corresponding to figure 3

从表2可清晰看出，与当前典型的五种去雾算法进行定量比较发现，所提出的方法在SOTS数据集上取得的PSNR平均值和SSIM平均值均为最高。值得一提的是，所提出的方法得到的PSNR平均值和SSIM平均值比排名第二的分别高出7.725 4 dB和0.066 6（见表2）。通过定性和定量的对比实验可得出，所提出的方法得到的去雾图像更接近标准清晰图像，图像修复的质量也是最好的，这验证了所提出的方法对于合成雾霾图像去雾的有效性。这些优势归因于所提出的改进型大气散射模型，通过在传统的大气散射模型中引入一个全局补偿系数，进而弥补了噪声对图像恢复带来的负面影响。

4.2 真实雾霾图像的实验结果

为评估所提出的方法对真实雾霾图像的去雾能力，在两个真实世界数据集上进行实验，这两个数据集分别为O-HAZE[33］数据集和IHAZE[34］数据集。在实验中，随机在这两个数据集中各选择两张图像进行实验，分别如图4和图5所示，并将所提出的方法与当前典型的五种方法的定性比较。其中，如图4和5中的（b）、（c）、（d）和（e）所示，这四种方法得到的去雾结果与标准清晰图像相比，即使在一定程度上实现了去雾，但都存在不足。这几种方法普遍存在偏暗、色彩失真、雾残留等问题。通过对比发现，Ju等[28］的去雾方法实现了去雾且避免了偏暗的问题，但由于其引入的光吸收系数存在缺陷，导致去雾结果中存在色彩失真且整体色调过亮（如图4（f）和图5（f）所示）。通过定性比较可知，本文所提出的方法与当前典型的五种去雾方法相比更优，所提出的方法不仅避免了去雾结果中存在的色彩失真和色调偏暗，而且与标准清晰图像也是最相似的。

图4 在O-HAZE数据集上不同算法的去雾结果Fig.4 Dehazing results of different algorithms on the O-HAZE dataset

为进一步清晰展示所提出的方法的优越性，与当前典型的五种去雾算法对比的客观评价指标见表3和表4，其中最优指标加粗显示。其中，表3是图4中不同方法得到去雾结果的PSNR值和SSIM值。表4是使用I-HAZE[34］数据集，各个方法得到去雾结果的PSNR平均值和SSIM平均值。从表3和表4的定量对比可知，与当前典型的五种去雾算法进行定量比较，所提出的方法均取得了最高的PSNR值和SSIM值。其中，所提出的方法得到的PSNR值和SSIM值分别比排名第二的高0.800 8 dB、1.675 3 dB、0.218 7 dB和0.104 9、0.086 0、0.025 1（见表3和表4）。定性和定量实验证明，所提出的方法对具有浓雾的真实雾霾图像依然具有很好的去雾能力，避免了去雾结果的色彩失真和整体色调偏暗等问题。由此，从侧面证明了所提出的方法具有很好的适用性。这些优势得益于提出的改进型大气散射模型避免了噪声光带来的负面影响；在图像修复的第一阶段，利用灰度世界算法求得的合理反照率为所提的方法具有很好的适用性提供了保障。

图5 在I-HAZE数据集上不同算法的去雾结果Fig.5 Dehazing results of different algorithms on the I-HAZE dataset

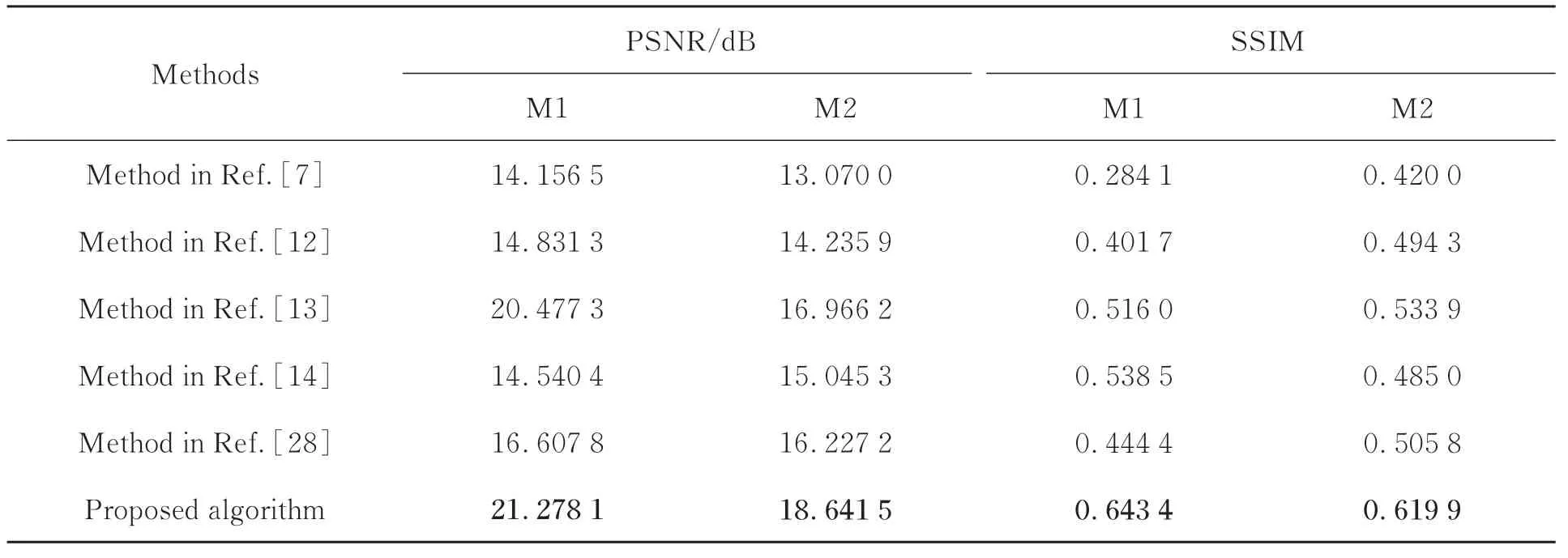
表3 与图4相对应的各去雾算法去雾结果的性能指标Tab.3 Performance metrics of dehazing results of various dehazing algorithms corresponding to Figure 4

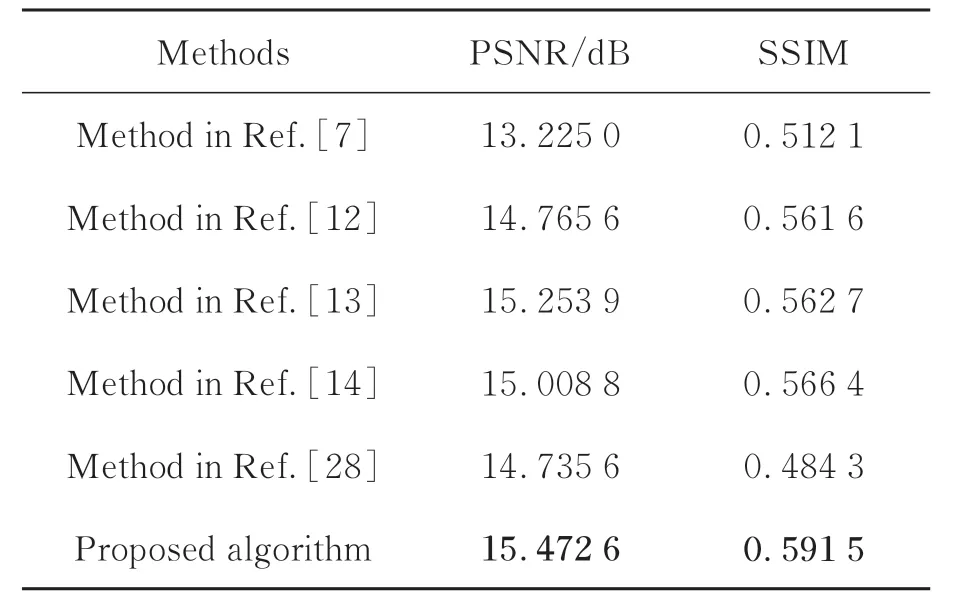
表4 在I-HAZE数据集上不同去雾算法去雾结果的性能指标均值Tab.4 Average performance metrics of dehazing results with different dehazing algorithms on the I-HAZE dataset

4.3 水下图像修复的实验结果

为进一步验证所提出的方法具有很强的适用性，在水下数据集UIEB[38］上进行实验，实验结果如图6所示。He等[7］的方法适用性不强，水下图像修复结果普遍偏暗且发生色彩失真（如图6（b）所示）；同样，Fu等[36］的方法亦发生严重的色彩失真（如图6（d）所示）。对比分析可知，Galdran等[37］的方法取得不错的修复结果，但其整体清晰度下降（如图6（e）所示），Ancuti等[35］的方法取得较好的视觉效果，但其图像细节过渡的不够平滑（如图6（c）所示）。通过定性对比实验可知，本文所提出的方法得到最好的视觉效果，且避免修复结果中出现色彩失真和细节丢失，同时可以发现所提出的方法得到的修复结果图6（f）与标准清晰图像图6（g）最为接近。

为更深入地证明本文所提出的方法具有很好的适用性并展示算法的优越性，与当前典型的四种水下图像修复方法对比的客观评价指标见表5，其中最优指标加粗表示。所提出的方法和其他四种水下图像修复方法的结果进行定量比较发现，所提出方法的PSNR值和SSIM值均是最高的，这说明所提出的方法相比于其他四种水下图像修复方法更加优越。同时，也进一步验证了所提出的方法具有很强的适用性。这得益于所得到的改进型大气散射模型和水下光学成像模型具有高的相似性，使得所提出的使用改进型大气散射模型的双阶段图像修复方法具有很好的适用性，既能实现图像去雾，又能实现水下图像修复。

图6 在UIEB数据集上不同算法的水下图像修复结果Fig.6 Underwater image restoration results of different algorithms on the UIEB dataset

表5 在UIEB数据集上不同水下图像修复算法修复图像的性能指标均值Tab.5 Average performance metrics of images restored by different underwater image restoration algorithms on the UIEB dataset

4.4 夜间图像增强的实验结果

通过大量实验发现，所提出的方法不仅能实现雾霾图像去雾，也能实现水下图像修复，并且均能得到优异的性能指标和不错的视觉效果。根据文献[17］可知，低照度图像的表征图像及直方图表征与雾霾图像具有很高的相似度，所以该改进型大气散射模型亦可用于夜间图像的修复。实验发现，所提出的方法确实可用于夜间图像增强，实验结果如图7所示。其中，图7中第一行是夜间图像，第二行是使用所提出的方法对夜间图像增强后的结果。经定性对比实验可发现，增强后的图像更清晰、对比度高，无色彩失真、展现出图像更多的细节。由此，更进一步证明所提出的 方法的确有很强的适用性。

5 结 论

针对传统的去雾方法和基于深度学习的去雾方法存在色彩失真、对比度下降和色调偏暗以及这些方法的适用性有限等问题，提出一种适用性强的图像修复方法——使用改进型大气散射模型的双阶段图像修复。通过引入一个全局补偿系数来弥补噪声光所带来的负面影响得到一个改进型大气散射模型，该模型避免了图像修复结果中存在的色彩失真和色调偏暗等问题。这得益于改进型大气散射模型和求取的合理反照率，使得所提出的使用改进型大气散射模型的双阶段图像修复方法具有很强的适用性。通过大量实验结果可证明，所提出的方法确实具有很好的适用性，既能有效实现雾霾图像去雾，又能实现水下图像的修复以及夜间图像增强，并且避免了最终的图像修复结果中存在色彩失真和偏暗等问题。不仅如此，所提出的方法在定量和定性实验上均取得了优异的结果。