大陆坡内波环境中声传播模态耦合及强度起伏特征*

高飞 徐芳华 李整林 秦继兴

1) (清华大学全球变化研究院地球系统科学系,地球系统数值模拟教育部重点实验室,北京 100084)

2) (海军研究院,天津 300061)

3) (中山大学海洋工程与技术学院,珠海 519000)

4) (中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)

大陆坡海域内波普遍存在,其陆坡地形和内波过程都会引起显著的声场起伏.已有研究工作主要关注内波或大陆坡单扰动因子对模态耦合和强度起伏的影响,少见将内波和海底地形起伏同时作为影响因子进行研究.文章考虑孤立子内波和海底地形对声传播的双重影响,首先构建海洋波导模型,然后基于简正波理论数值对比分析各波导模型条件下模态的耦合规律,进而研究声场强度起伏特性及其物理机理.研究结果表明,当声波朝向或远离内波中心传播时,模态耦合在内波与大陆坡的共同作用下出现耦合增强或衰减,高号模态耦合系数振荡;内波扰动的作用使得能量由低号模态耦合至高号模态,提高了声场强度衰减;斜坡的作用使得声波下坡传播时,波导模态数增加、模态强度衰减降低;大陆坡内波环境中的模态强度总和大于内波环境、小于大陆坡环境,且模态组间的能量转移比只有内波或者大陆坡时更强,高号模态从耦合中获得更多能量,使得跃层以上水层能量增强.

1 引言

内波(又称内重力波)是发生在分层流体内部的波动,其振幅、波长、周期变化较大,通常分别在10—1—102m,102—105m 和数分钟-数小时尺度范围[1].起伏的海底地形是内波生成的关键要素之一[2],内波在海洋中广泛存在,而大陆坡海域中孤立子内波活动尤为频繁[3,4].大陆坡内波环境中,水体起伏变化造成声速场的水平扰动,同时伴随水深的变化,海水声速和地形两者共同作用于声场起伏.关于内波和大陆坡波导环境中的声场强度起伏规律及其物理机理一直是水声学领域的热点研究问题,也有大量的相关研究工作报道.

存在内波的波导环境中,声场能量的空间分布和时变特性异常.声传播路径与内波波阵面夹角较大时,简正波模态发生强烈耦合,模态能量在各模态间发生耦合转移,高号简正波获得能量后快速衰减,导致声场能量起伏加剧[5-8].声波以较小角度通过内波时(或声传播方向平行于内波波阵面),内波会引简正波聚焦或发散,并伴随产生“瞬态声道”和声影区等特殊现象[9-12].内波是海洋中的一种动态过程,当声源和接收位置固定,连续内波传播过程中,会造成简正波模态耦合和强度起伏具有时域上的(准)周期性[13-16].

对于规律且周期变化的海底沙丘地形,简正波模态特征值之差等于周期性海底地形起伏的波数时,将产生“频率共鸣”[17],且海底地形对声场强度的衰减作用随起伏高度、周期而增加[18];水深单调均匀变化时,简正波模态耦合使得能量趋于水深增加的方向转移,且能量可更好地保留在波导环境中而非向海底泄露[19];海洋向陆地“舌状”延伸时,第二类到达波主要为海洋与陆地侧交界面的水平折射波[20].

在实际海洋环境中,大陆坡海底地形可引发形成内波,大陆坡内波波导环境在海洋中分布广泛,简正波模态耦合与强度变化同时受内波与海底地形变化的影响,但同时考虑二者的影响相关研究相对较少.Chiu等[21]通过研究声孤立子内波从深水区向大陆坡传播时的声场特性,指出简正波在大陆坡与内波的共同作用下产生耦合增强,其结果使得非邻近模态间能量转移加剧,导致进入内波边界上层的能量增加了2—4 倍,此文中未涉及模态强度及其衰减机制.

本文重点从简正波模态耦合和强度起伏的角度进行研究,总结声波在大陆坡海洋向下传播经过内波中心前后耦合系数随水平距离的变化特征,对比分析大陆坡内波环境与跃层、孤立子内波、海底斜坡单个扰动因子影响下的模态强度总和及分组模态强度的差异,可更好地解释大陆坡内波环境中模态耦合及强度起伏的物理机理.

2 声场理论及环境模型

2.1 耦合简正波理论

存在孤立子内波且海底水平变化环境中,简正波模态函数ϕm具有对水平距离r的依赖性,柱坐标系中任一点声压p(r,z) 可描述为式中,

(4)式为单向耦合近似得到的表达式,为第j区间内的第n阶模态函数,为第j+1 区间内第m阶模态与第j区间内第n阶模态的耦合系数,用于计算模态间幅度的耦合传递,其大小与相邻两区间内的模态特征函数、特征值有关.大陆坡内波环境中声速及水深的变化导致模态函数的变化,从而使得简正波各模态间不满足正交性,是模态耦合的主要原因.

对于点源条件,简正波初始模态幅度为

式中,zs为声源深度,利用(1)式—(5)式逐区间积分计算可得到模态幅度和声压场p(r,z).综合(2)式—(5)式可知,在水平变化海洋环境中,影响简正波模态幅度随距离变化的因素主要包括模态能量衰减损失((3)式)、模态耦合((4)式)和受声源激发的模态初始幅度((5)式),波导环境的水平变化导致简正波局地模态函数和特征值的变化,模态函数的变化导致模态耦合,模态特征值的变化导致衰减损失的扰动,进而造成模态强度起伏.

2.2 大陆坡内波声速场模型

浅海背景声速(温度)剖面c0(z) 在垂直方向上通常可简化成3 段结构(图1),表层0 至跃层上界面zu混合均匀,声速值可视为常数cu;跃层上边界zu至跃层下边界zl,声速(温度)由cu(Tu)迅速较小至cl(Tl);跃层下边界zl至海底zb,声速由cl缓慢减小至cb,不失一般性,下文在仿真中将该段也视为混合层,即cl=cb.

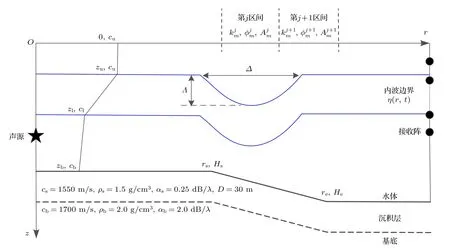
图1 大陆坡内波波导环境参数示意图Fig.1.Diagram of parameters for continental slope internal wave waveguide environment.

在分层海洋水体介质中,水体质点受到扰动后垂向位移与其浮力频率N(r,z)成正比,浮力频率越大的水层水质点振动的频率越大,N2(r,z)=gρ-1∂ρ/∂z=g(αT∂T/∂z+βS∂S/∂z),其中T,αT,S,βS分别为温度、热膨胀系数、盐度、盐度收缩系数.跃层对应的水层浮力频率较大,于是内波在水平方向的扰动可近似认为是跃层的扰动,内波扰动导致跃层上下边界产生垂向位移,跃层的边界对应于内波的边界.

内波造成的水平变化环境中的声速场c(r,z) 可用背景声速场c0(z) 和扰动场声速 δc(r,z) 之和描述,即c(r,z)=c0(z) +δc(r,z).对浅海条件下KdV 方程进行求解,可将二维孤立子内波边界分布及其时变特征描述为双曲正割函数的形式[24]:

式中,Λ,r0,Δ,v分别表示内波的幅度、中心距离、波宽、传播速度,η0表示内波边界深度的最小值,受孤立子内波频散关系的约束,Λ与Δ通常呈反比关系.

构建两层海底声传播仿真环境如表1,水体声速跃层位于15—35 m 间,声速由1530 m/s 减小至1500 m/s,其余深度声速均匀,密度、衰减系数分别为1.0 g/cm3,0 dB/λ.海底沉积层声速、密度、衰减系数、厚度分别为1550 m/s,1.5 g/cm3,0.25 dB/λ,30 m.基底层声速、密度、衰减系数分别为1700 m/s,2.0 g/cm3,2.0 dB/λ.声源频率为200 Hz.孤立子内波中心位于大陆坡上方,斜坡坡度为2.86°.

表1 仿真环境参数配置Table 1.Configuration of environment parameters for simulations.

为对比分析内波与大陆坡对模态耦合和强度的影响,基于图1 和表1 构建四种仿真环境参数设置,如图2 所示.环境1 (图2(a))为无内波、无大陆坡的水平不变跃层波导环境,环境2 (图2(b))为内波波导环境,环境3 (图2(c))为大陆坡波导环境,环境4 (图2(d))为大陆坡内波波导环境,后续仿真计算四种环境声学特性时其他输入条件保持一致.

图2 仿真用四种典型海洋环境 (a) 环境1(跃层环境);(b) 环境2(内波环境);(c)环境3(大陆坡环境);(d) 环境4(大陆坡内波环境)Fig.2.Four typical environments for simulation: (a) Environment 1 (thermocline);(b) environment 2 (internal wave);(c) environment 3 (continental slope);(d) environment 4 (continental slope internal wave).

结合(6)式与图2 分析内波引起的声速场扰动可知,声速以3 km为中心对称分布.计算内波环境下的声速梯度场,结果如图3 所示,可见水平声速梯度以3 km为中心反对称分布,小于3 km范围内,水平声速梯度为正值,且随距离先增大后减小,极大值约为0.12 s—1,出现在2.8 km 处;大于3 km 范围内为负值,且随距离先减小后增大,极小值为—0.12 s—1,出现在3.2 km 处;内波中心处水平声速梯度为0.

图3 内波环境水平声速梯度分布Fig.3.Distributions of horizontal sound speed gradient in internal wave environment.

3 结果与分析

3.1 模态耦合系数分析

在声场计算过程中,将水平距离划分为多个等间距区间,若相邻两个区间j,j+1 水平间距Δr足够小时,声传播环境参数变化小,则远大于.依据图2 中所示的环境参数,水平区间取Δr=20 m,计算各种环境条件下的耦合系数,并取其实部.经计算,水深由大陆坡坡上100 m 向坡下增加至200 m 过程中,局地简正波模态数目由34 阶增加至67 阶.

3.1.1 模内传导系数分析

图4为第1—4 号简正波模态在内波(环境2)、大陆坡(环境3)、大陆坡内波(环境4)三种波导环境中,模内耦合系数随距离的变化曲线.在三种波导环境中,高号简正波比低号简正波对波导环境的变化更为敏感,图4 各分图中总体趋势为,说明当波导环境的水平变化时,高号简正波模态函数的垂向结构变化率更大.

内波波导环境2 中,简正波模态耦合系数正比于声速水平梯度[25,26]δc(r,z)/c0(z),声速场和水平声速梯度分别以3 km 处的孤立子内波为中心对称分布和反对称分布,声波向内波中心传播时为正水平声速梯度,声波远离内波中心传播时为负声速梯度,故内波环境中以3 km为中心对称分布(图4 中虚线),极小值点对应于水平声速梯度极大值点.

图4 第1—4 号简正波在不同波导环境中水平距离2—4 km 处的模内传导系数 (a) 1 号模态;(b) 2 号模态;(c) 3 号模态;(d) 4 号模态Fig.4.The intra-mode conduction coefficients of mode 1,2,3 and 4 at range 2—4 km in different waveguide environments:(a) Mode 1;(b) mode 2;(c) mode 3;(d) mode 4.

大陆坡波导环境3 中,水深由100 m 均匀增加至200 m,总体呈上升趋势(图4 中点线),说明随着环境水深的均匀增加,相邻两区间内的同号简正波相似程度增加.

大陆坡内波波导环境4 中,受内波和大陆坡的共同作用,但大陆坡内波波导环境对的影响并非是内波和大陆坡两种单因子环境的乘积,例如图4(d)中大陆坡内波波导环境中的4 号简正波与系数乘积明显的不一致.对比图4 中不同波导环境中的曲线,随着模态号的增加,水平距离3 km 以内大陆坡内波环境中与内波环境的差异逐渐增强,且曲线波谷显著增强,说明大陆坡内波波导环境相比内波波导环境,声下坡并向内波中心传播过程中存在模内耦合减弱;水平距离大于3 km 后,声下坡并向远离内波中心传播,曲线波谷显著减弱或消失,大于内波或大陆坡单因子波导环境中的值.

3.1.2 模间耦合系数分析

此处需要说明,大陆坡内波波导对模态耦合系数的主导影响因子与具体内波强度、大陆坡坡度等因素相关,上文段落中提及的主要影响因子在其他波导环境中不可一概而论.

3.1.3 讨论

水平变化波导环境中,模态耦合系数也可用声速和水深的水平梯度来描述[13,19]:

式中,ρw,ρs,H分别为水体密度、沉积层密度和水体深度,其余参数符号及其含义与第2 节中一致,等号右侧第一项为内波扰动作用,第二项为海底地形起伏作用.(7)式忽略了环境变化的高阶小量,当波导环境水平扰动较大时,其计算精度会有一定程度的下降[27],但可用于对模态耦合的物理机制进行解释.

模态耦合系数与各号简正波模态函数密切相关,模态函数在复杂波导情况下难以解析,但低号模态函数结构相对简单,可以通过分析其在大陆坡、内波波导环境中的变化趋势,对模态耦合系数进行估计,用于解释其物理机制.图6为内波、大陆坡、大陆坡内波三种波导环境中,不同距离处的局地简正波1 号模态.

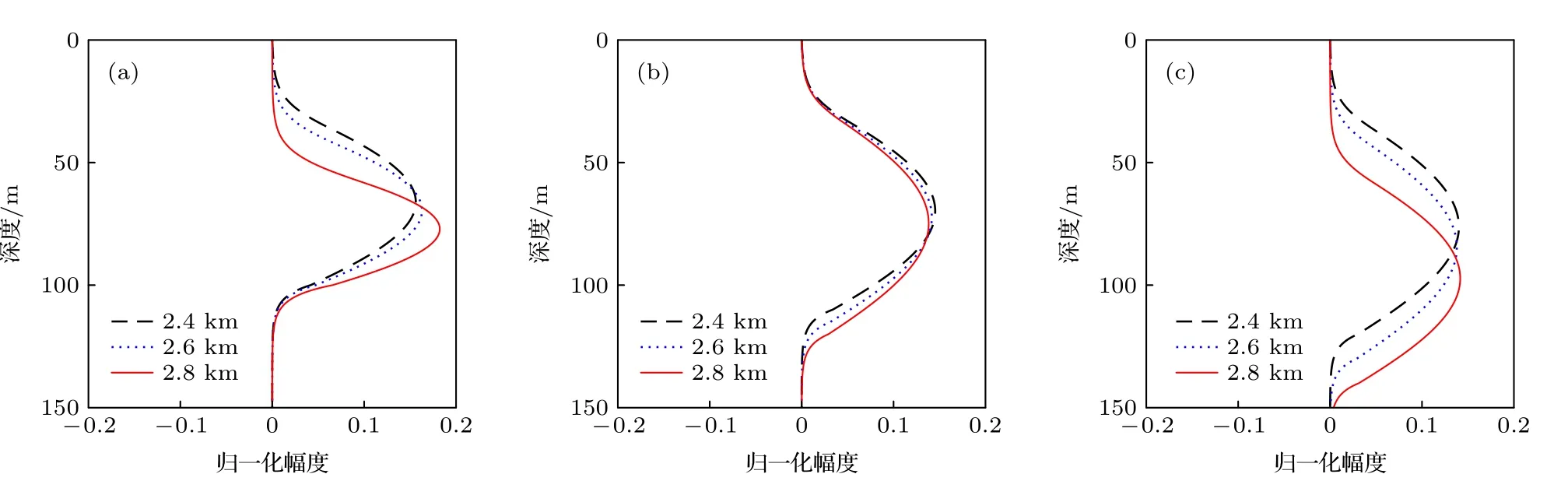
图6 不同波导环境中1 号局地模态函数 (a) 内波环境;(b) 大陆坡环境;(c) 大陆坡内波环境Fig.6.The local function of mode 1 in different waveguide environments: (a) Internal wave environment;(b) continental slope environment;(c) continental slope internal wave environment.

在水平距离2.4—2.8 km 范围内,声波向内波中心传播,由内波引发的跃层边界向深度增加方向转移,跃层以上混合层加厚,且声速值相对跃层以下水体较大.若将水平间距很小范围内的水体和海底视为一根张力不均匀的“弹性绳”,“弹性绳”由上至下分为四个部分,分别为混合层、跃层、弱梯度层、海底.内波的作用使得近海面混合层增厚,导致“弹性绳”上部张力较大部分的长度增加,其结果是低号简正波模态在跃层附近的起振点向深层移动(图6(a)).声下坡传播过程中水深增加,使得跃层下层低声速层增厚,导致“弹性绳”中部张力较小长度增加,其结果是低号简正波模态在海底附近的起振点向深层移动(图6(b)).

在大陆坡内波环境中,“弹性绳”的张力属性由大陆坡、内波共同决定,在声下坡向内波中心传播过程,低号简正波模态浅层和深层两端的起振点都向深层移动,相当于模态函数整体向深层移动(图6(c)),并伴随模态函数形状的变化,内波和大陆坡的作用对模态空间结构变化起到相互增强的作用,其结果是低号模态的模内传导系数减小、模间耦合系数增加.同理,可对声下坡并远离内波中心传播时的模内传导系数进行解释.

3.2 模态强度起伏分析

对于水平变化波导环境中的声场,第j+1 区间内m号模态强度是第j区间内同号模态的能量传导与异号模态间的能量耦合转移((2)式),本文定义m号模态强度为Im(r)=10lg(Am(r)“*”为共轭复数符号.依据耦合简正波理论,空间扩展损失无关波导环境的水平变化,故在计算中将其去除,不影响分析波导环境的变化对模态幅度的影响;为有效激发低号模态的初始幅度,将声源深度设置为60 m(＞跃层深度);基于图2 中构建的4 种波导环境,计算各号简正波模态幅度,并转化为对数声强(单位为dB),图7为前20 号模态强度随距离的变化.

跃层波导环境1 中,低号简正波初始强度得到有效激发,高号模态衰减速率大于低号模态,前6 号模态为波导模态(图7(a)中红色点虚线),各号简正波模态强度随水平距离单调递减,跃层波导环境水平无变化,各距离处的局地模态函数和特征值一致,模态间无耦合与能量转移.

简正波声场由各模态成分组成,各模态声场幅度在水平变化波导环境中的起伏共同影响整个声场.在水平变化波导环境中,模态的能量源于其同号模态的模内能量传导和不同号模态的模间能量耦合,由于模间能量耦合的方向不一,导致模态强度曲线的振荡.例如在大陆坡内波波导环境4 中(图5 中红色实线),呈振荡变化,耦合系数的正负值反映出1 号模态分别与2 号、3 号、5 号、13 号模态间耦合时能量的转移方向与大小.故一般情况下各号简正波模态强度随距离变化曲线无单调性,且特征规律不完全一致.

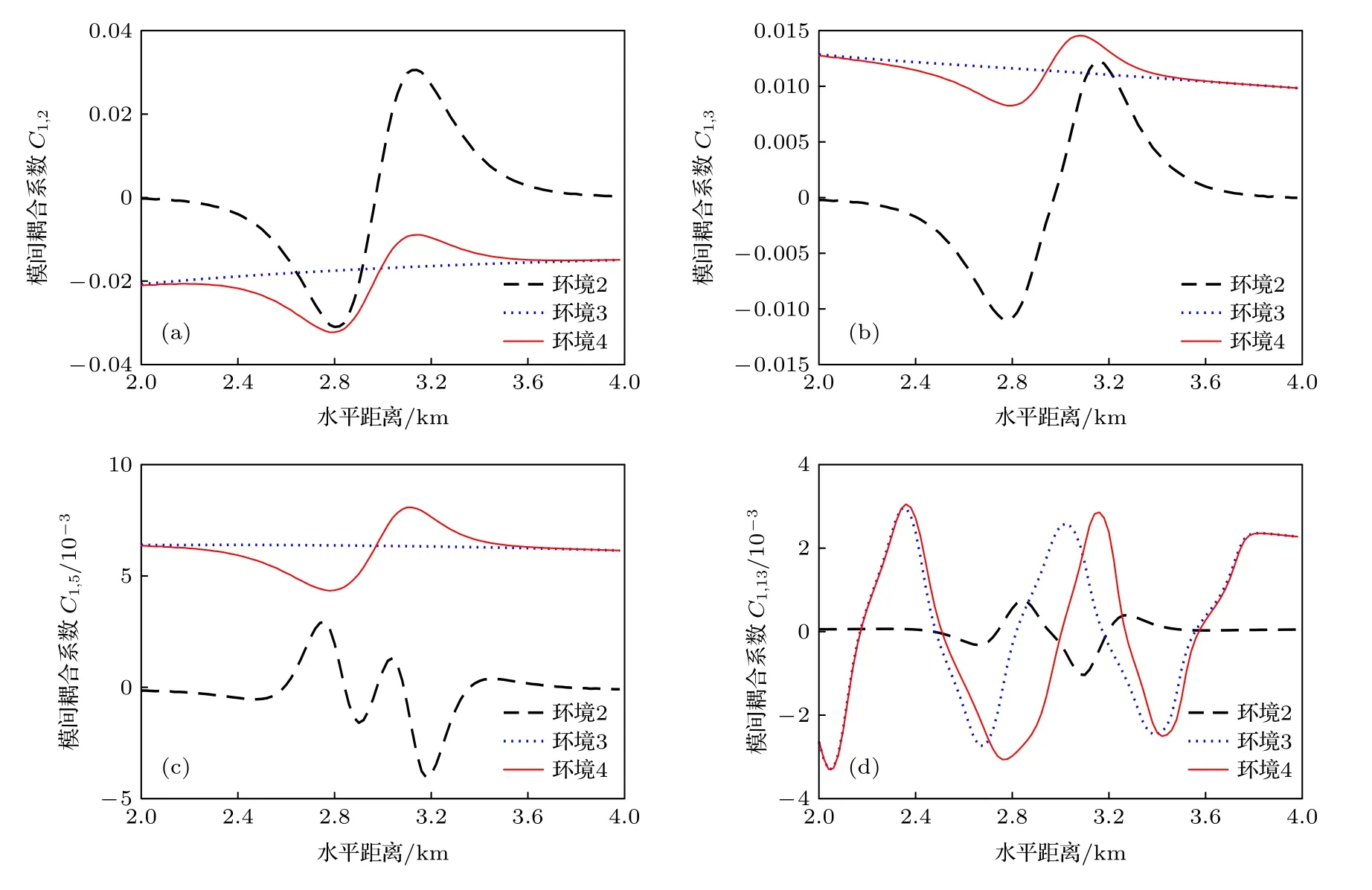
图5 不同波导环境中水平距离2—4 km 处的模间耦合系数 (a) 1 号与2 号模态;(b) 1 号与3 号模态;(c) 1 号与5 号模态;(d) 1 号与13 号模态Fig.5.The inter-mode coupling coefficients at range of 2—4 km in different waveguide environments: (a) Mode 1 with 2;(b) mode 1 with 3;(c) mode 1 with 5;(d) mode 1 with 13.

然而,由于简正波能量的守恒性和各号模态能量衰减特性的差异,使得各模态间的能量转移方向具有一般性规律.对比内波波导环境(图7(b))与跃层环境(图7(a))各号模态强度,可知对于7 号以上的多数高号模态,由于模态间能量转移使其能量值显著增加,在6 km 处的内波环境中的7—13 号的各阶模态能量(图7(b)中蓝色实线)比跃层环境中(图7(a)中蓝色实线)增加了4 dB 以上.故能量耦合转移的总体趋势是低号模态将能量转移至高号模态,模态耦合使得高号简正波在模态耦合中获得能量而强度增加,低号简正波在模态耦合中失去了能量而强度减小.

图7 不同波导环境中1—20 号简正波模态强度随距离变化 (a) 跃层环境;(b) 内波环境;(c) 大陆坡环境;(d) 大陆坡内波环境,红色点划线为1—6 号模态,蓝色实线为7—13 号模态,黑色点线为14—20 号模态Fig.7.Modes 1—20 intensity variation with range in different waveguide environments: (a) Thermocline environment;(b) internal wave environment;(c) continental slope environment;(d) continental slope internal wave environment,the red dotted lines,blue solid lines and black dotted lines represent mode groups of 1—6,7—13 and 14—20,respectively.

对于高号简正波模态,由于其衰减较快,在远场模态强度小,即同号模态内的能量传递很小,其能量主要来自于与低号模态间能量耦合转移,耦合而来的能量在一定水平传播距离范围内快速衰减,故能量向高号模态耦合会使得整个声场的总能量减小.图8为内波环境中的第8 号、11 号模态声场强度分布,其中8 号模态声场传播至1.2 km 处强度衰减至—100 dB 以下,在3 km 附近由于内波引发模态耦合获得能量,声场增加至约—87.5 dB,之后随着传播距离又快速衰减至—100 dB 以下.同理,11 号模态在3 km 附近也通过模态耦合获得能量,最大声场能量增加至约—94.3 dB.

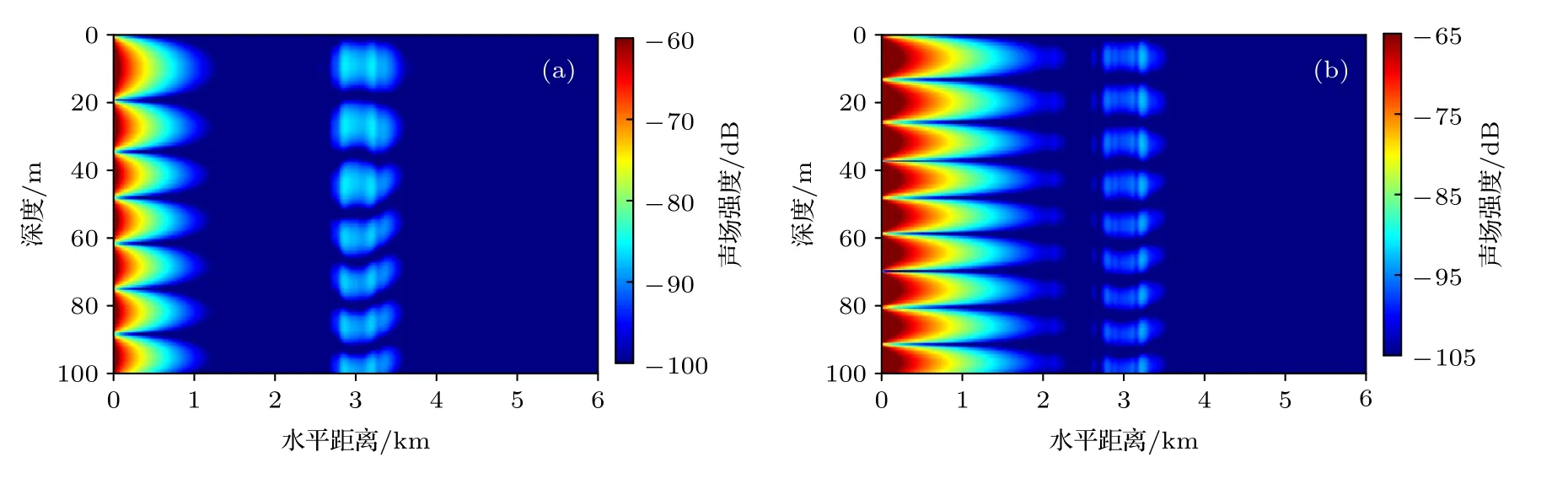
图8 内波波导环境中8 号(a),11 号(b)简正波模态声场强度分布Fig.8.The mode 8 (a) and mode 11 (b) intensity versus range and depth in the internal wave environment.

声波在大陆坡波导环境3 中水平距离2—4 km下坡传播,水深由100 m 均匀增加至200 m,水深的增加使得简正波模态数增加,同时模态特征值实部增大、虚部减小,波导模态由6 个增加至13 个(图9),波导模态数的增加、模态特征值虚部的减小,减小了声波能量在大陆坡波导环境中的衰减速率.当声传播至2 km 处开始下坡传播,模态耦合的整体效果使得能量由1—6 号模态转移至7—13 号模态,7—13 号模态强度开始增加;同时,由于模态虚部减小,降低了模态能量的衰减速率,使得7—13 号非波导模态在经过大陆坡下坡波导环境后转变为波导模态(图7(c)).

图9 大陆坡波导环境中不同水平距离前13 号简正波模态特征值分布,特征值实部大于横虚线为波导模态Fig.9.Eigenvalues of the first 13 modes of different ranges in the continental slope environment.

值得一提的是,在大陆坡波导环境中,14 号以上模态也通过模态耦合从低号模态得到能量,故模态能量耦合转移的总体趋势是从低号模态向高号模态仍成立.

大陆坡内波波导环境4 同时包含内波和水深变化两种模态强度扰动因子,声波向内波中心传播,内波造成正声速梯度;声波远离内波中心传播,内波造成负声速梯度,结合大陆坡的作用,模内能量传导系数、模间能量耦合系数出现震荡,模态耦合在两种扰动因子的共同作用下出现增强或消减(图7(d)),各模态强度的变化趋势和特征还需进行针对性分析,无统一的变化规律.为便于讨论,分组计算模态幅度的欧几里德范数,并转化为对数声强,第m—n号简正波声强Im—n(r)为

I1—max是所有模态能量的总和,表征波导环境对声波的传导能力,由于波导环境的水平变化,导致能量在简正波模态间的耦合转移,各阶模态强度衰减特性存在差异,进而造成不同波导环境的整个声场强度扰动.图10(b)中内波环境2 中的I1—6小于跃层波导环境,说明内波的作用使得1—6 号模态在模态耦合中能量减小,而图10(d)中内波波导环境2 中I14—max大于跃层波导环境,说明内波的作用使得14 号以上模态在模态耦合中能量增大,验证了上文中内波扰动使得能量从低号波导模态耦合转移至高号非波导模态的结论.而高号非波导模态衰减强,从模态耦合中获得的能量在传播过程中快速衰减,从而导致内波扰动使得整体声场能量下降,图10(a)中内波波导环境2 中的I1—max最小.

图10 不同波导环境中各组模态强度之和随距离变化 (a) 所有模态 I1—max;(b) 1—6 号模态 I1—6;(c) 7—13 号模态 I7—13;(d) 14 号以上模态I14—maxFig.10.The sum of intensity of each mode groups versus range in different environments: (a) I1—max;(b) I1—6;(c) I7—13;(d) I14—max.

大陆坡增加了波导模态数,同时减小了模态特征值的虚部降低了模态强度衰减速率,图10 中大陆坡波导环境3 中的I1—max,I1-6,I7—13,I14—max均大于跃层波导环境,说明大陆坡的整体作用是增强了波导环境对声能量的传导能力.然而,对于单个模态仍会存在由于模态耦合导致其强度减弱的现象(图7(c)).

从各号模态能量总和来看,大陆坡内波波导环境中模态强度受内波扰动减弱和大陆坡增强共同作用,其I1—max大于内波波导环境,小于大陆坡波导环境(图10(a)),在不同水平距离范围内对模态耦合起到主要作用的影响因子不一致.

仿真环境构建的孤立子内波中心位于3 km处,波宽Δ=300 m,大陆坡在2—4 km 水平距离范围坡度为1/10.小于2.7 km 的水平距离内,大陆坡、大陆坡内波波导环境中的模态强度曲线几乎一致(图10),大陆坡为主要影响因子;2.7—3.3 km 范围内,对于低号波导模态内波是主要影响因子,内波引发的模态耦合使得I1—6快速减小(图10(b)中红色曲线加粗段),其损失的能量补充到高号模态,尤其是新增波导模态I7—13(图10(c)中红色曲线加粗段).

同时,通过对比可知大陆坡内波波导环境中,内波和大陆坡两种扰动因子对模态间能量耦合转移起到增强的效果.对于1—6 号波导模态,大陆坡内波波导环境加速了能量从1—6 号模态向高号模态转移,导致在4 种波导环境中,大陆坡内波波导环境中的I1—6最小;对于7—13 号新增波导模态,大陆坡内波波导环境使其在模态耦合中获得了更多的能量,造成在4 种波导环境中,大陆坡内波波导环境中的I7—13最大.

大陆坡内波波导环境中模态间能量耦合转移增强是3.1 节中耦合系数增强的一种验证,但由于3.1 中主要分析的是同号模态间和两个模态间的耦合系数,且模态间能量耦合转移不能单纯以耦合系数来判断其起伏.分析大陆坡内波环境中各号模态在2.7—3.3 km 范围内的变化特征,如图11 所示,4 号模态强度大幅减小,6—8 号模态强度增幅较大,是导致I1—6与I7—13能量变化的主要来源;3.1 节中分析指出相邻模态间能量耦合转移更强,而4 号模态并非直接将能量转移至7 号和8 号模态,而是首先与临近的5 号和6 号模态耦合,进而通过其将能量转移至7 号和8 号模态,符合Chiu等[21]对模态间能量转移过程的论述.

3.3 模态强度起伏对环境参数敏感性分析

为进一步分析大陆坡内波波导环境参数的变化对简正波模态耦合和强度起伏的影响,本节进行参数敏感性分析,通过改变坡度、内波幅度和宽度参数,计算不同环境中参数变化条件下的低号模态组I1-6的强度之和(图12).由于各简正波模态能量之和I1-max守恒,故I1—6起伏也对应了简正波高、低号模态组间的能量转移.其中,图12(a)和图12(b)分别为2—4 km 水平距离范围内坡度由2/50 增加至8/50 时,大陆坡内波、大陆坡波导环境中的I1—6变化曲线;图12(c)和图12(d)分别为内波幅度在15—50 m 范围内变化时,大陆坡内波、内波波导环境中的I1—6变化曲线;图12(e)和图12(f)分别为内波宽度在150—550 m 范围内变化时,大陆坡内波、内波波导环境中的I1—6变化曲线.

图12 不同环境中参数变数时的模态强度之和 I1—6 随距离的变化 (a),(c),(e) 大陆坡内波环境;(b) 大陆坡环境;(d),(f) 内波环境Fig.12.The sum of intensity I1—6 versus range in different environments of various parameters: (a),(c),(e) Continental slope internal wave environment;(b) continental slope environment;(d),(f) internal wave environment.

由对比结果可知,随着坡度、内波幅度增加和内波宽度的减小,低号模态组强度起伏增强,说明简正波高、低号模态组之间能量转移增强.对于内波幅度和宽度参数,其变化对简正波模态耦合和能量转移的作用不同.当内波幅度增加,造成的声速场水平梯度增加,增强了简正波模态耦合与模态组间的能量转移;而当内波幅度一定时,内波宽度增加引发声速场水平梯度减小,导致简正波模态耦合和能量转移减弱.

同时,对比图12 中左侧子图与右侧子图,可知大陆坡内波环境造成的模态强度起伏大于单独大陆坡环境或内波环境的影响,与上文中大陆坡内波环境导致模态耦合与能量转移增强相对应.

高号模态能量衰减较快,较远距离处的声场能量主要由低号模态贡献.声波在大陆坡区域下坡传播过程中,由于水深的增加,会导致低号模态函数向深层移动,从而使得声能量垂向分布不均匀,跃层以上形成声影区(图13(a),(c),(e)).在大陆坡内波环境中,由于内波和大陆坡两个因素的共同影响,导致模态耦合与能量转移增强,高号模态从低号模态获得能量,和低阶模态相比,高阶模态函数在全水深范围内均是振荡的,其能量垂向分布较均匀,从而增加了跃层以上的声场能量(图13(b),(f)).经计算结果的对比,大陆坡内波环境中(图13(f))跃层以上区域(深度0—35 m,水平距离2—6 km)声能量是大陆坡环境中(图13(e))的1.7—3.5 倍,可提高跃层上层的声学探测能力.

图13 不同环境中的声场分布 (a),(c),(e) 大陆坡环境3 中的所有模态、1—6 号模态、7—max 号模态声场;(b),(d),(f) 大陆坡内波环境4 中的所有模态、1—6 号模态、7—max 号模态声场.其中,图中虚线方框标记了0—35 m 深度、2—6 km 水平距离的区域Fig.13.The sound field in different environments: (a),(c),(e) The sound fields of the whole modes,models 1—6 and modes 7—max in continental slope environment,respectively;(b),(d),(f) the sound fields of the whole modes,models 1—6 and modes 7—max in continental slope internal wave environment,respectively.The white dashed boxes mark the area of 0—35 m and 2—6 km horizontal distance.

4 结论

本文构建跃层、内波、大陆坡、大陆坡内波4 种波导环境模型,基于耦合简正波理论,研究了海底地形和孤立子内波对声传播的双重影响,分析了大陆坡内波波导环境中200 Hz 声源的简正波模态耦合系数和强度起伏特征,主要研究结论如下.

1)模态耦合系数受内波、大陆坡两个扰动因素共同作用,两种扰动因子导致的模态耦合系数变化趋势一致时,耦合系数得到增强;不一致时,耦合系数的正负值由主要扰动因子决定.

2)当波导环境受到扰动时,高号简正波剥离效应在现象上会起主导作用,模态耦合的总体趋势是能量由低号模态向高号模态转移,由于高号模态能量衰减快,内波扰动降低了波导环境的能量传导能力,声波下坡传播时,波导模态数增加模态衰减速率降低,提高了波导环境的能量传导能力.

3)大陆坡内波波导环境中,模态能量总和大于内波环境、小于大陆波导环境,模态间的能量耦合转移增强,低号模态组向高号模态组转移更多的能量,增加了了跃层以上水层的声场能量.

依据耦合简正波理论,模态强度取决于其同号简正波的能量传导,以及与其它所有异号简正波间的能量转移,且复杂环境条件下的模态函数难以解析,模态强度的变化是一个强非线性过程,故文章暂未针对某一号模态强度开展具体分析,后续将结合实验数据开展深入研究.

感谢西北工业大学谢磊老师关于耦合简正波理论给予的指导.