类锂离子体系自旋四重态费米接触项的精密计算*
魏向杰 孙邓 王黎明† 严宗朝
1) (河南师范大学物理学院,新乡 453007)
2) (Department of Physics,University of New Brunswick,Fredericton E3B 5A3,Canada)
费米接触项与原子超精细结构常数有密切关系,往往对原子能级的超精细劈裂起主要贡献.波函数在原点处的行为以及电子之间的关联效应是影响费米接触项计算精度的两个主要因素.对于一般的原子体系来说,费米接触项的高精度计算不是一件容易的工作.本文利用Hylleraas 坐标下的Rayleigh-Ritz 变分法求解了 锂原子 和类锂离 子体系(Z=4—10)自旋四 重态 1 s2s3s 4S,1 s2s4s 4S 和 1 s2s2p 4P 的薛 定谔方程,得到的非相对论变分能量收敛精度达到10—13.根据所得到的高精度变分波函数,计算了这些体系的费米接触项,并研究了原子核的有限质量对结果的影响.费米接触项的精度达到了10—10.本文结果可以作为其他理论方法的参考基准,同时也为相关的实验研究提供了参考数据.
1 引言
一直以来,少电子原子分子体系(氢原子、氦原子、氢分子离子等)的精密光谱研究为检验基本物理理论、测定基本物理常数(里德伯常数R∞、精细结构常数α等)、确定原子核的电荷分布半径和磁矩分布半径等提供了有效的方法[1-4].锂原子以及类锂的铍离子(Be+)作为三电子原子体系,受到了理论和实验研究者的广泛关注.锂原子精密光谱的一个重要应用是确定原子核的性质,如核电核分布半径和磁矩分布半径(Zemach 半径)等.例如,Yan 和Drake[5]发展了锂原子能级的精密计算理论和方法.根据他们的方法,锂原子最低的三个能级(2S,3S 和2P)间的跃迁频率的同位素移动的高精度理论计算值和实验值的对比被用于确定锂原子核同位素的电荷分布半径,特别是具有“晕核”结构的11Li 的电荷分布半径[4](这里的电荷分布半径指的是相对于某个电荷半径为已知的同位素的相对电荷分布半径,目前的理论计算值的精度还不足以确定锂原子核的绝对电荷分布半径).对于铍离子(Be+),也有类似的应用[4].Puchalski 和Pachucki[6]则发展了锂原子超精细结构的高精度计算理论和方法,根据他们计算的锂原子基态的超精细结构劈裂理论值与实验值的比较发现,7Li 原子核的Zemach 半径比6Li 的大40%,为原子核结构的研究提出了一个重要的问题.最近,基于锂离子(Li+)的超精细结构的研究也得到了相似的结论[7].
超精细结构是原子精密谱研究的一个重要内容.对于原子体系的磁偶极超精细结构来说,其最主要的来源是费米接触相互作用.因此,要想得到高精度的超精细结构劈裂,必须要把费米接触项计算到足够高的精度[6,7].对于类氢原子体系,费米接触项(Fermi contact term,fc)可以由解析计算获得;而对于含有两个电子或更多电子的原子体系,fc只能通过数值计算得到,其数值精度严重依赖波函数在原点处的质量.除此之外,电子间的关联效应也会对fc产生重要影响.通过使用全局化方法[8,9],可以降低fc对波函数在原点附近行为的依赖性;而通过使用Hylleraas 型变分波函数,则可以充分照顾到电子关联效应对fc的影响[10].目前,利用全局化方法和Hylleraas 变分波函数,锂原子基态(1s22s2S)非相对论fc的理论计算值的精度已经达到了10—8[6,11];对于锂原子的其他几个较低的自旋双重态,fc的值也可以达到很高的精度[11].对于锂原子的自旋四重态,Yan[12]用Hylleraas 变分波函数计算了 1 s2s3s4S,1 s2s4s4S和1s2s5s4S这三个态的fc,精度高达10—8;King[13]也做了类似的计算(包括1s2s6s4S),但是与Yan 的结果相比,精度稍差.Zhuo 及其合作者[14,15]用组态相互作用方法计算了类锂离子体系(Z=7—10)几个较低的自旋四重P 态(1 snlnl′4Po和1s2pnp4P)的费米接触项以及其他超精细结构常数.对于fc,他们的结果的精度在10—5(通过和本研究小组的结果对比而发现).本文对锂原子及类锂离子体系(Z=4—10)的1s2s3s4S,1 s2s4s4S和 1s2s2p4P的费米接触项做了计算,一方面弥补了在Z=4—6这个区域中相关数据的缺失;另一方面,对于文献上已有的结果,在精度上有明显的提高(1—3 个量级).除此之外,还研究了原子核的有限质量对fc的影响.本文所有fc的精度都在10—10以上,可以作为其他计算方法的基准,同时也为相关的实验研究提供了有价值的参考数据.
2 理论方法
2.1 非相对论哈密顿量
在质心坐标系中,三电子原子体系的非相对论哈密顿量为[16](本文使用原子单位,即ℏ=e=me=1)
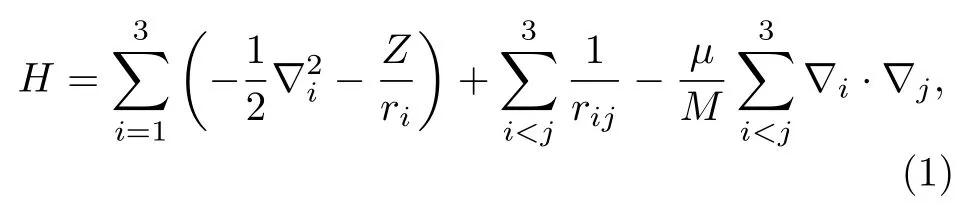
其中,M代表原子核的质量,µ=meM/(me+M)代表电子的折合质量.(1)式中能量的单位是 2RM,而RM=(1-µ/M)R∞.原子核的有限质量对能量的影响通过能量单位 2RM(mormal mass shift)和(1)式中的最后一项(specific mass shift)体现出来.
2.2 三电子体系Hylleraas 型变分波函数
本文使用瑞利-李兹变分法求解体系的薛定谔方程,选择三电子体系的Hylleraas 型基函数构造变分波函数.Hylleraas 型基函数是目前求解两电子和三电子原子体系薛定谔方程的精度最高的基函数[17].把体系的变分波函数做如下展开:
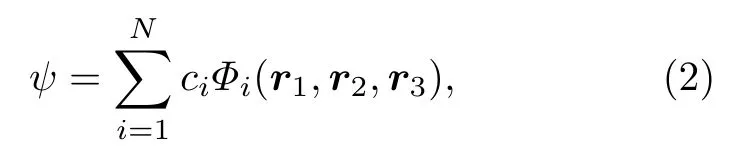
而
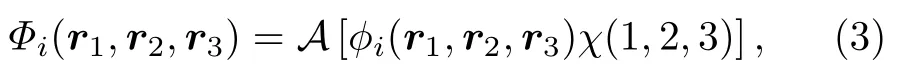
其中,A表示三电子体系的反对称化算符,ϕi(r1,r2,r3)表示基函数的轨道部分:
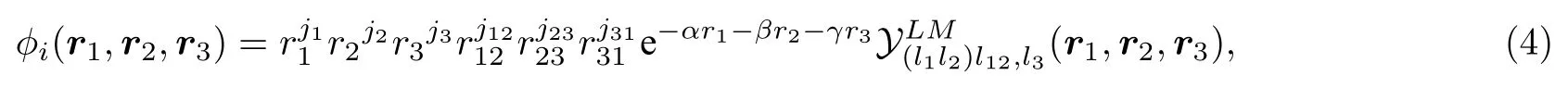
而
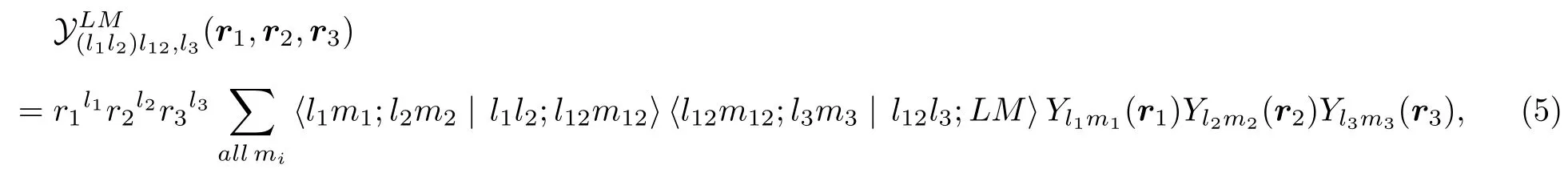
表示三个角动量函数耦合出的基函数的角向部分;χ(1,2,3)表示自旋函数,对于自旋四重态(S=3/2,MS=3/2),有
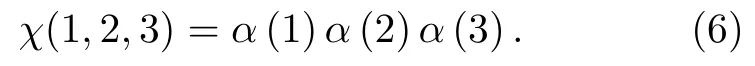
使用(2)式的变分波函数,根据瑞利-李兹变分法[17],可以得到广义本征值方程:

其中H和O分别表示哈密顿矩阵和交叠矩阵.求解广义本征值方程(7),即可得到体系的能量本征值和本征波函数的最佳近似值.为了提高变分能量的收敛率,参考Yan 的方法[12],根据以下条件把变分基底分为5 组:
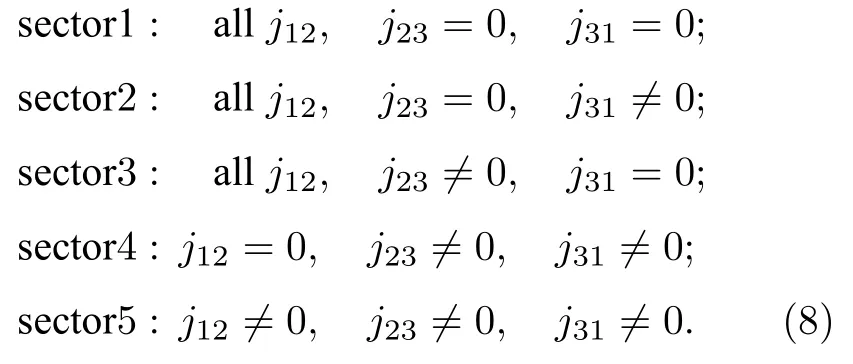
每组基底的规模用下面的条件控制:
其中,jµ,jµν和Ωi均取非负整数.
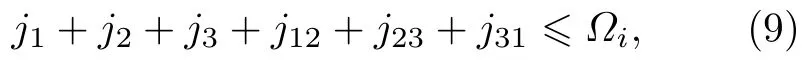
2.3 费米接触项与全局化方法
费米接触项的定义为
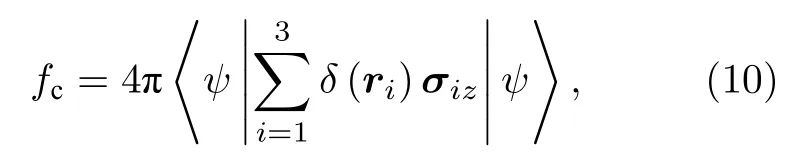
其中σz是泡利矩阵.从(10)式可知,fc的数值精度对体系波函数在坐标原点处的取值有比较强的依赖关系,这在数值计算中是不利的.为了克服这一缺点,Hiller 及其合作者以及Drachman 发展了“全局化方法”[8,9].本文采用Drachman 的全局化方法[9],其主要思想是用一个等价的表达式代替δ函数的期望值,即
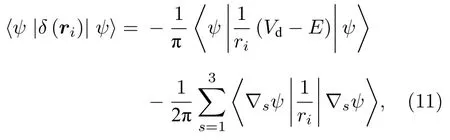
其中
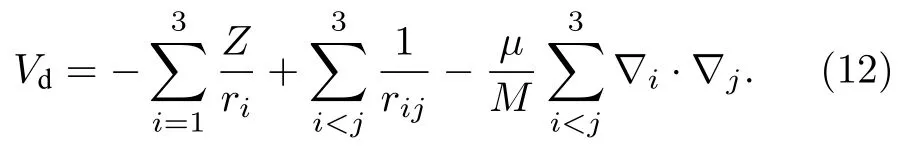
不难发现,利用全局化方法计算得到的fc比直接利用定义(10)式计算在精度上可以提高1—2 个量级.
3 结果与讨论
使用2.2 节中描述的变分基底,首先用瑞利-李兹变分法求解锂原子和类锂离子体系(Z=4—10)的 1 s2s3s4S,1 s2s4s4S 和 1 s2s2p4P 的薛定谔方程,得到了这些体系的变分能量和变分波函数.把变分基底的规模从N=210 (N表示基函数的数目)逐步扩大到N=27130,在每一组基底下,用牛顿法对5 组非线性参数进行充分优化,以得到尽可能低的变分能量.在N<10000 的情况下,优化参数能够带来比较明显的效果,但是,随着变分基底的进一步增大,优化参数带来的能量降低很有限.这时,主要靠增大基底的规模带来能量的进一步降低.
表1 列出了锂原子 1 s2s3s4S 态的变分能量(原子核质量取为无穷大)在不同基底下的值,从收敛序列可以确认变分能量的收敛精度达到了10—13.对于其他两个态,变分能量也达到了相似的精度.表2列出了从锂原子到Ne7+离子的 1 s2s3s4S,1s2s4s4S和 1 s2s2p4P 的变分能量,并与文献上已有的结果进行了对比.相较于Yan[12]的结果,本研究组的结果在精度上提高了1—3 个量级;相较于Barrois等[18]的结果,则提高了5—6 个量级.精度提高的主要原因是使用了更多的变分基函数.
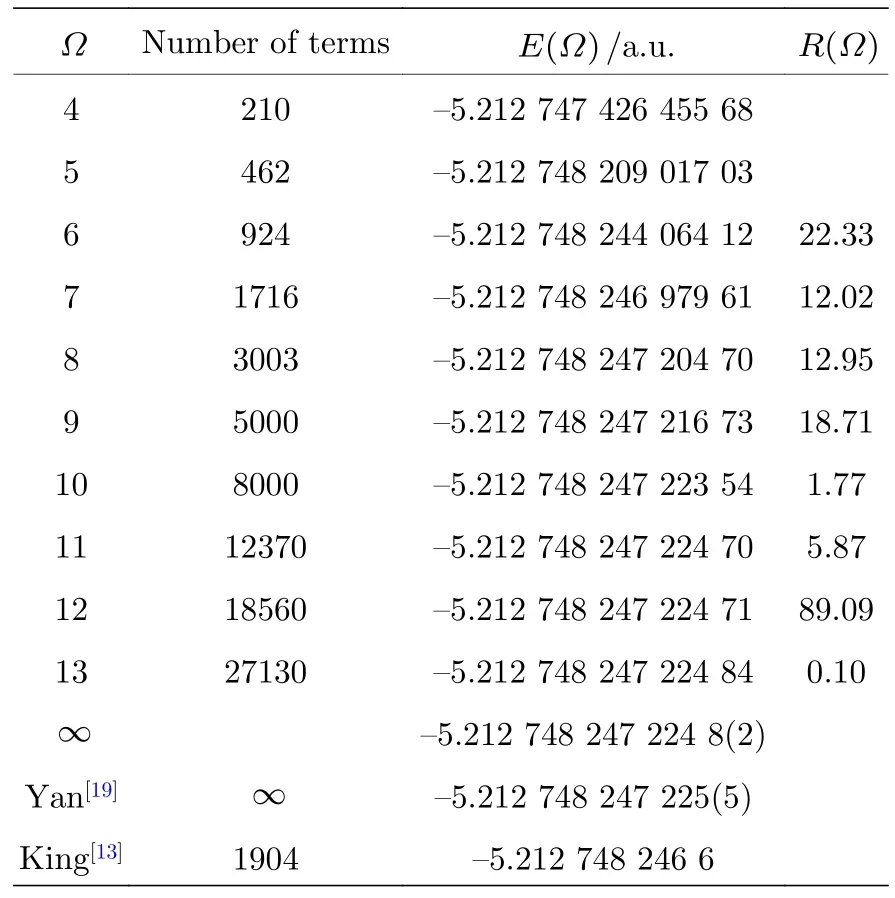
表1 锂原子 1 s2s3s 4S 态的非相对论变分能量的收敛情况,核质量取为无穷大Table 1.Study of the convergence of nonrelativistic variational energies of the 1 s2s3s 4S state of lithium atom,suppose the mass of the nucleus is infinite.
表1 和表2 中的变分能量都是在原子核质量取无穷大的假设下得到的,即在方程(1)中取µ/M=0.对于原子核质量取有限值的情况,可以通过直接对角化方程(1)中的哈密顿量来得到体系的能量,也可以用微扰法来处理有限核质量带来的影响,即把方程(1)中的最后一项当作微扰算符来处理.为了得到各种同位素的能量,使用计算公式
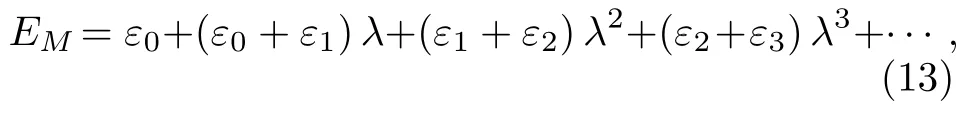
其中,EM表示核质量为M的同位素的变分能量;ε0表示核质量取无穷大时体系系的能量;ε1,ε2和ε3分别表示一阶、二阶和三阶质量极化系数;λ=-µ/M.质量极化系数可以通过微扰论计算得到.用微扰论计算了一阶、二阶和三阶质量极化系数,数据列于表3.根据表2 和表3 中的数据,只要知道了核质量,就可以根据方程(13)计算出该同位素的非相对论能量.
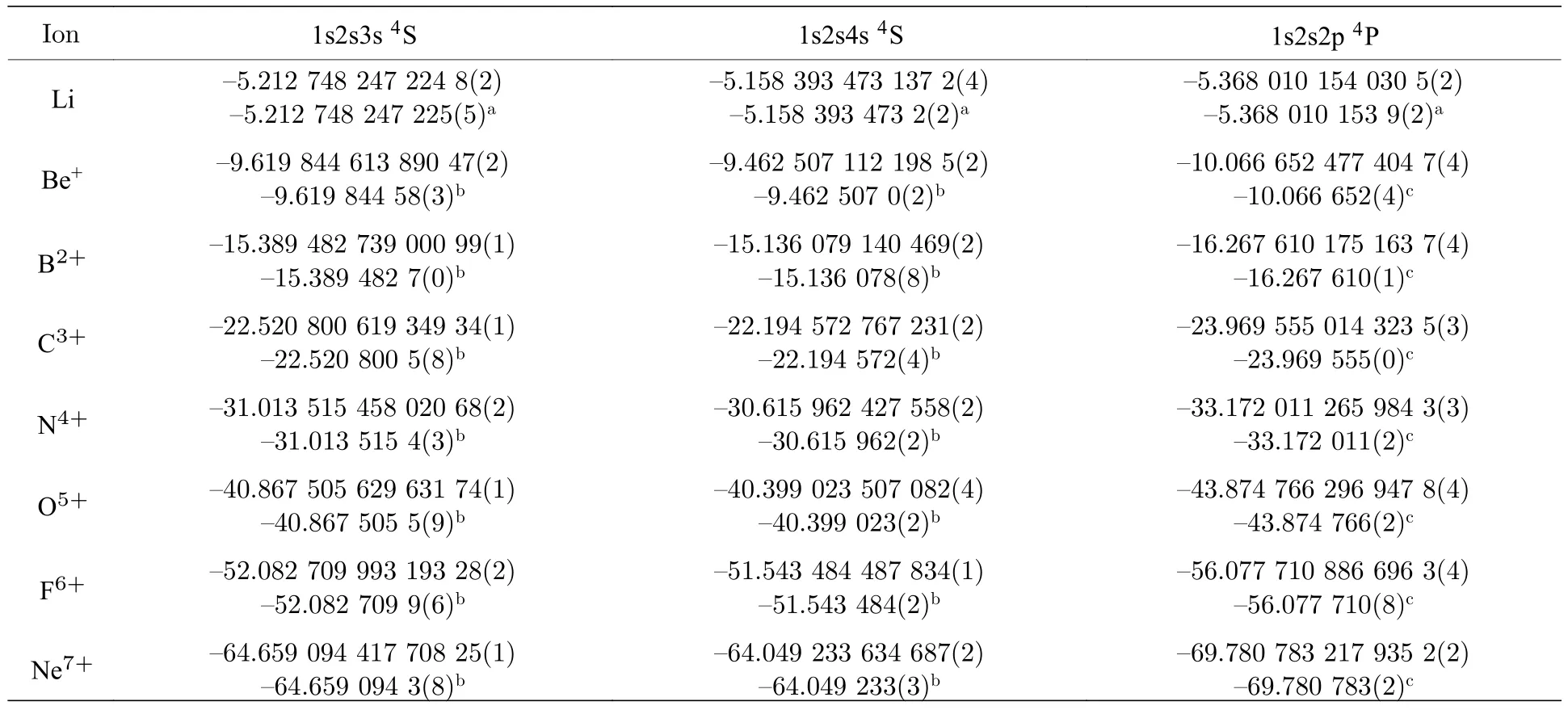
表2 类锂离子体系 1 s2s3s 4S,1 s2s4s 4S 和 1 s2s2p 4P 态的非相对论能量,核质量取为无穷大 (原子单位)Table 2.Nonrelativistic energies of the 1 s2s3s 4S,1 s2s4s 4S and 1 s2s2p 4P states of lithium-like ions,suppose the mass of the nucleus is infinite (in a.u.).
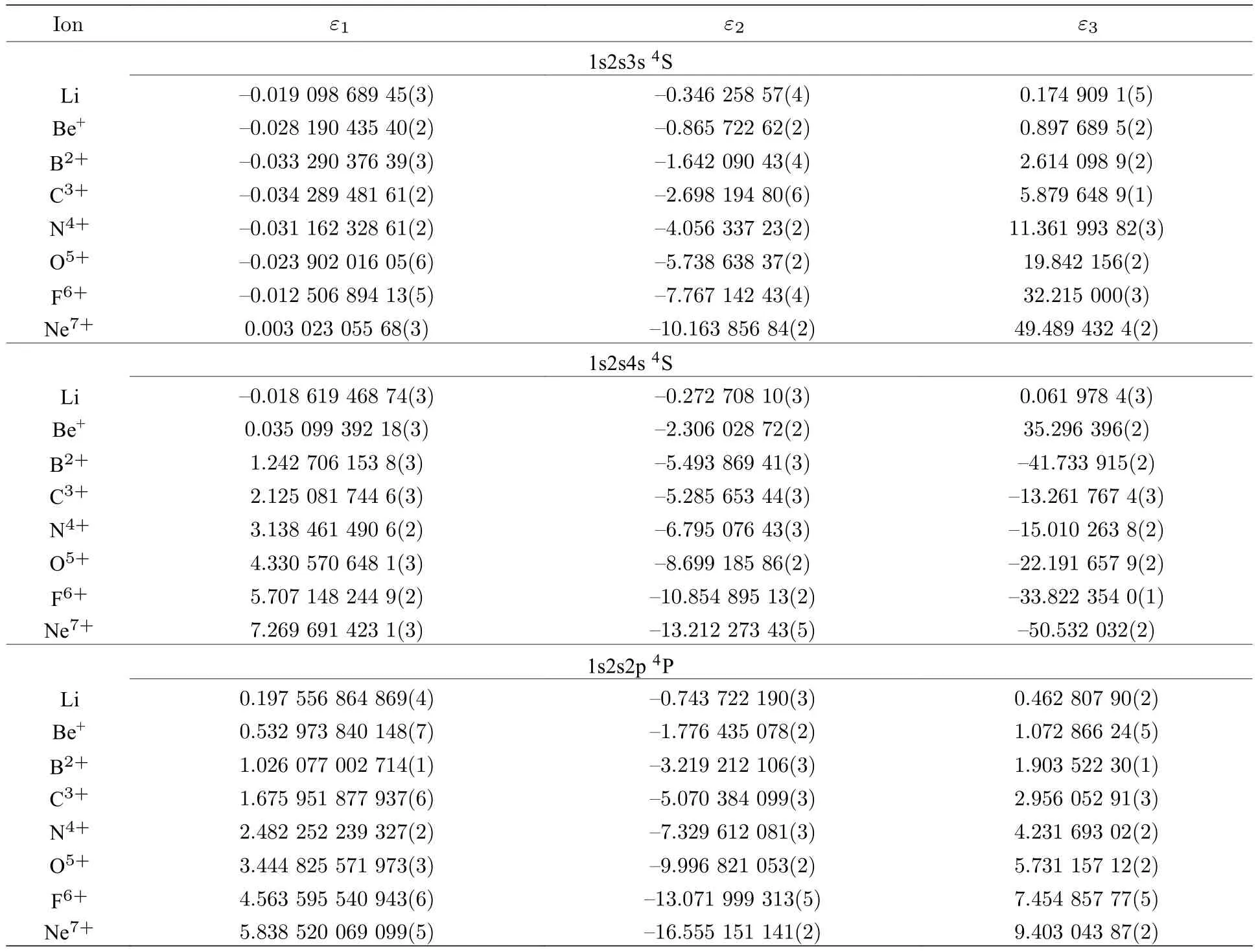
表3 类锂离子体系 1 s2s3s 4S,1 s2s4s 4S 和 1 s2s2p 4P 态的质量极化系数(原子单位)Table 3.Mass polarization coefficients of the 1 s2s3s 4S,1 s2s4s 4S and 1 s2s2p 4P states of lithium-like ions (in a.u.).
根据变分法得到的高精度波函数以及方程(10)和方程(11),即可得到fc的数值.表4 列出了锂原子的fc随基底逐渐增大而收敛的情况.根据收敛序列,可以确定fc的收敛精度达到了10—10.表5 列出的是从锂原子到Ne7+三个最低的自旋四重态的fc.这些结果的收敛精度普遍达到了10—10.与早期使用Hylleraas 变分波函数计算的锂原子费米接触项[12,21]相比,本研究组的结果在精度上提高了2—5 个量级.精度提高的原因有两点: 一是在变分波函数中包括了更多的基函数;二是使用了Drachman 全局化方法[9],这种方法有利于加速结果的收敛.通过比较Zhuo等[14,15]使用组态相互作用方法计算的N4+,O5+,F6+和Ne7+的1 s2s2p4P 态的费米接触项,发现他们的结果的精度在10—5左右.
表4 和表5 中的fc是在核质量取无穷大的情况下得到的,与核的有限质量对变分能量的影响类似,核的有限质量对fc的影响也可以通过质量极化系数表示为
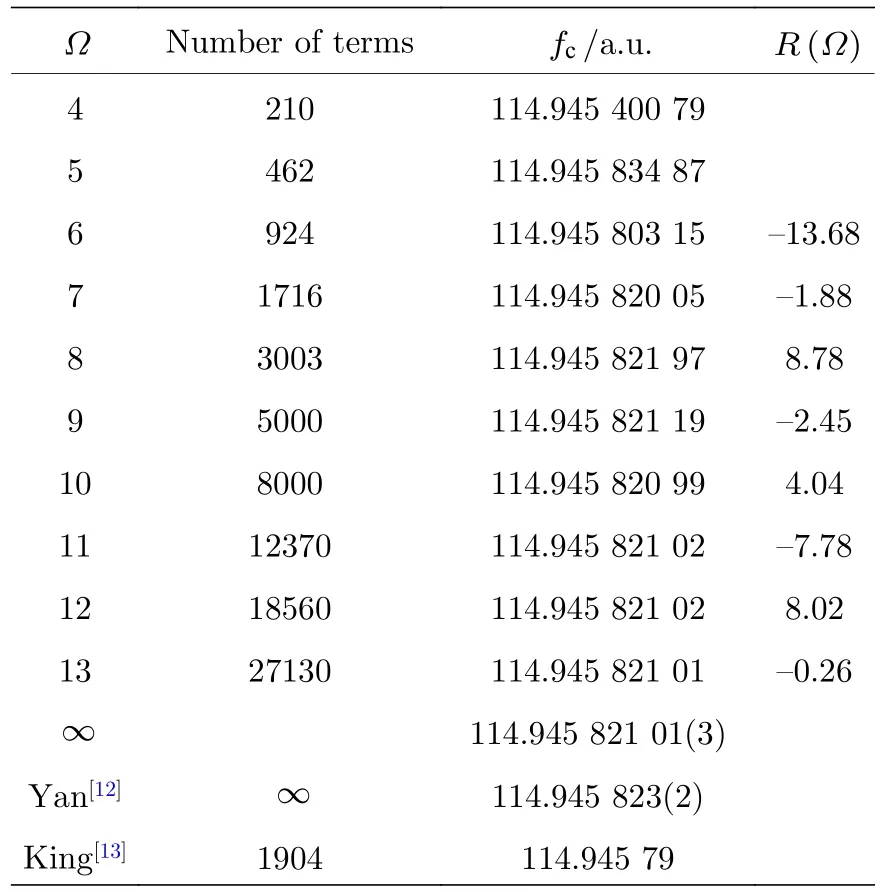
表4 锂原子 1 s2s3s 4S 态的费米接触项的收敛情况,核质量取为无穷大Table 4.Study of the convergence of nonrelativistic variational energies of the 1 s2s3s 4S state of lithium atom,suppose the mass of the nucleus is infinite.
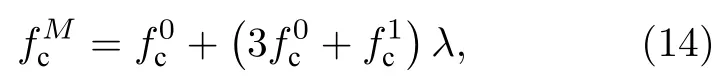
其中,表示无穷大核质量情况下计算得到的费米接触项,表示有限核质量下的费米接触项,表示费米接触项的一阶质量极化系数.方程(14)精确到O(λ).计算得到的费米接触项的一阶质量极化系数列于表6.根据表5 和表6 所列的数据可以看出,原子核的有限质量对fc的影响主要来自于即normal mass shift,质量极化效应的影响相对来说要小很多.
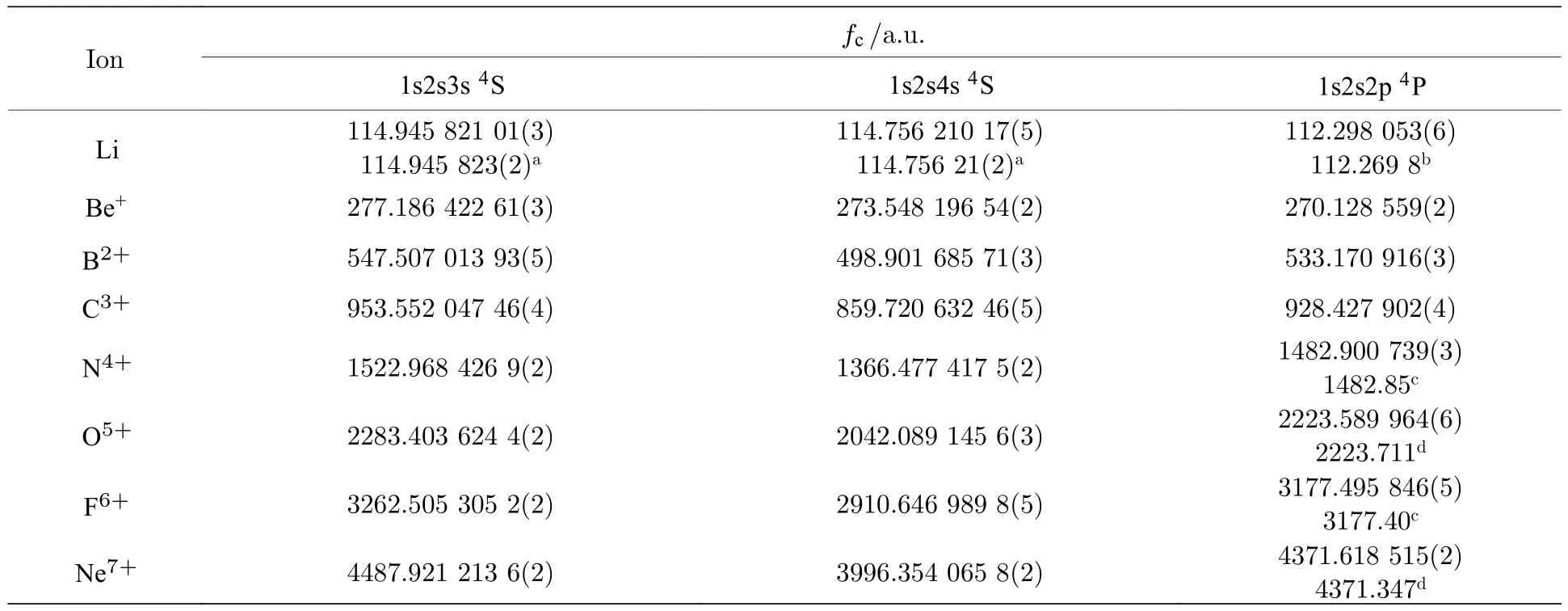
表5 类锂离子体系 1 s2s3s 4S,1 s2s4s 4S 和 1 s2s2p 4P 态的费米接触项,核质量取为无穷大Table 5.Fermi contact terms of 1 s2s3s 4S,1 s2s4s 4S and 1 s2s2p 4P states of lithium-like ions,suppose the mass of the nucleus is infinite.
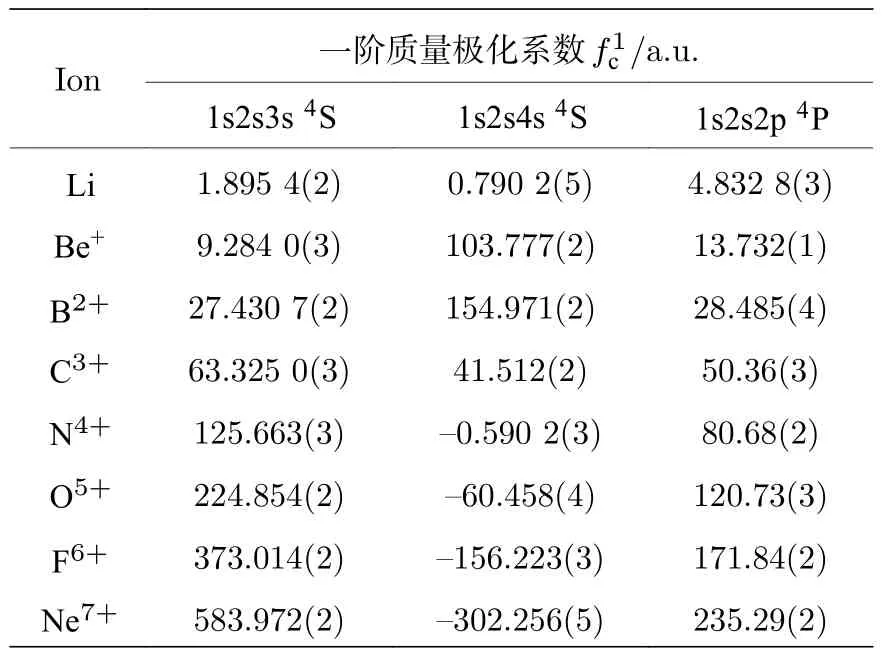
表6 类锂离子1s2s3s 4S,1 s2s4s 4S 和1s2s2p 4P态的费米接触项的一阶质量极化系数Table 6.First-order mass polarization coefficients of Fermi contact terms of 1 s2s3s 4S,1 s2s4s 4S and 1s2s2p 4P states of lithium-like ions.
4 结论
本文利用Hylleraas 坐标下的瑞利-李兹变分法对锂原子及类锂离子(Z=4—10)的自旋四重态 1 s2s3s4S,1 s2s4s4S 和 1 s2s2p4P 的非相对论薛定谔方程进行了高精度求解,得到的变分能量的精度达到了10—13,并给出了变分能量的一阶、二阶和三阶质量极化系数.与文献上已有的结果相比,本文的结果在精度上提高了1—6 个数量级.使用高精度的变分波函数,计算了这些态的费米接触项,fc的精度达到了10—10,是目前已有结果中最精确的.本文的结果可以作为其他计算方法参照的基准,也为以后要开展的相对论修正和QED 修正计算工作打下了基础,同时也为相关的实验研究提供了有价值的参考数据.

