基于改进灰狼算法优化BP神经网络的住宅工程造价预测研究
付家棋,胡国杰
(辽宁工业大学 经济管理学院,辽宁 锦州 121001)
在建筑工程拟建之前,工程项目的造价预测对可行性分析与项目决策起着重要的作用。在传统的估算方法中,工程造价的从业人员通过各省颁布的投资估算指标,对工程造价进行预测,由于受到造价人员职业素养和主观性的影响,工程造价的预测效果并不理想。人工神经网络具有良好的拟合能力,可以较为准确地预测拟建项目的工程造价,预测的数据可以为工程估算提供有效的参考,郝艳芬等[1]采用BP神经网络实现了市政工程的造价预测。但是,BP神经网络存在着搜索能力差、对初始位置较为敏感的缺陷[2]。为加强神经网络的全局探索能力,潘雨红等[3]运用遗传算法优化BP神经网络,为其赋予最佳的初始迭代位置,加快了收敛速度,准确地预测了公路工程的造价。陈小丽[4]采用粒子群算法优化BP神经网络,实现了高层住宅工程的造价预测。
2014年Mirjalili等[5]提出了灰狼优化算法(Grey Wolf Optimization Algorithm,GWO)。灰狼算法具有设置参数少和寻优能力强的优点,在预测的准确度和算法时间方面具有良好的表现。但是,灰狼算法存在着种群多样性单一、全局探索和局部搜索能力不易协调、过早收敛的缺陷。为了改进算法的性能,Nadimi-Shahraki等[6]提出了改进灰狼算法(Improved Grey Wolf Optimizer,I-GWO)。I-GWO采用了一种名为维度学习的搜索策略(Dimension Learningbased Hunting,DHL),增强了灰狼种群的多样性,平衡了全局探索和局部搜索的能力。
本文将主成分分析降维处理的数据输入到IGWO-BP模型中进行训练,通过与其他模型进行对比分析和误差评价分析,验证I-GWO-BP模型的有效性。
1 住宅工程造价指标的确定
为展开住宅工程的造价预测,需要输入一组可以代表工程特征的数据,这些数据不仅能直接反映建筑工程的特点,而且还是影响建筑工程造价的重要因素。按照各分部工程对工程造价的重要性程度,对工程造价指标进行初步选取。通过查阅资料,并对梁喜等[7-16]学者的文献进行分析,根据造价指标的重要性程度与获取难易程度进行筛选,最终选取出14项造价指标,同时对定性指标进行量化处理,具体指标见表1。

表1 住宅工程造价指标量化表
2 I-GWO-BP预测模型
2.1 灰狼算法
灰狼的种群中存在着特定的等级制度。在算法的搜索过程中,每次迭代时最佳的3只灰狼被定义为α,β和δ,其引导其余的灰狼ω在搜索空间中搜寻猎物。灰狼算法的寻优过程为包围猎物、狩猎跟踪、攻击猎物。
(1)灰狼包围猎物的模型如下

式中:D表示个体与猎物之间的距离;Xp表示猎物的位置向量;X表示灰狼的位置向量;t表示当前的迭代的次数,式(2)表示灰狼位置的更新公式。A和C是系数向量,由式(3)和式(4)计算。

式中:r1和r2是[0,1]之间的随机值;a为收敛因子。在迭代过程中从2线性减少到0。
(2)灰狼有协作包围猎物的能力,由适应度最佳的灰狼α,β和δ带领其余灰狼进行位置更新。灰狼个体的猎物跟踪模型如下

式中:Dα,Dβ,Dδ分别表示灰狼α,β和δ与其他灰狼ω个体之间的距离;Xα,Xβ,Xδ分别代表灰狼α,β和δ的当前位置;C1,C2,C3的值由式(4)所计算。
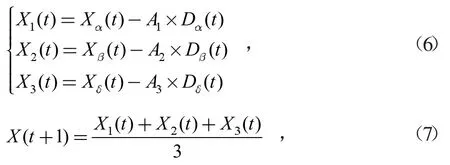
式中:X1(t)表示灰狼ω个体朝向灰狼α更新的步长;X2(t)表示灰狼ω个体朝向灰狼β更新的步长;X3(t)表示灰狼ω个体朝向灰狼δ更新的步长。灰狼ω个体最终的更新位置由式(7)所确定。
经过不断的迭代与更新,猎物最佳的位置将会被确定,即灰狼α所处的位置。
2.2 改进灰狼算法
灰狼算法是在寻优的过程中每只灰狼通过最佳的灰狼引导来进行位置更新的,这就导致了灰狼算法种群多样性差,易早熟收敛。为了克服灰狼算法的这些缺陷,Nadimi-Shahraki[6]提出了一种选择和更新相组合的搜索策略。这种搜索策略名为维度学习。DLH的搜索策略提高了全局搜索能力,改善了种群多样性。改进灰狼算法的搜寻过程为初始化、移动、选择和更新。
(1)初始化阶段:I-GWO进行初始化操作,将N只灰狼随机分布在搜索空间内,其范围为[lj,uj]。初始化模型如下

式中:lj和uj分别代表搜索边界的上下限;randj[0,1]为0到1之间的随机值。
第i只灰狼在第t次迭代中的位置为实值向量Xi(t)={Xi1,Xi2,…,XiD},由适应度函数f(Xi(t))计算,其中D为问题的数量。初始化后的狼群被储存在N行D列的Pop矩阵中。
(2)移动阶段:DLH搜索策略与GWO算法搜索策略都会产生一个候选位置来引导灰狼进行位置更新。Xi-GWO(t+1)是GWO算法引导灰狼位置更新的第一个候选位置,由式(7)所计算。首先,在DLH搜索策略中,灰狼个体是向邻域内不同的灰狼和Pop种群内随机选择的灰狼学习的。计算灰狼个体的邻域半径,模型如下

式中:邻域的半径Ri(t)表示的是当前灰狼位置Xi(t)与候选位置Xi-GWO(t+1)之间的欧氏距离。
然后,在此邻域内所有的灰狼表示为Ni(t),其中Di为Xi(t)与Xj(t)之间的欧氏距离。

最后,DLH搜索策略为灰狼Xi(t)提供另一个更新的候选位置,表示为Xi-DLH(t+1),模型如下

式中:Xi-DLH,d(t+1)的第d维是由Ni(t)中随机选择的灰狼XN,d(t)的第d维与Pop种群中随机选择的灰狼Xr,d(t)的第d维进行计算的。对灰狼的第d维执行此操作后,迭代计数器加1,直到达到最大的迭代次数D完成候选位置的更新操作,其中D为问题的维数。
(3)选择和更新阶段:通过比较Xi-GWO(t+1)与Xi-DLH,d(t+1)的适应度值来选出最佳的候选位置。如果最佳候选位置Xi(t+1)的适应度值优于灰狼个体Xi(t),则进行位置更新,否则,灰狼Xi(t)的位置保持不变。
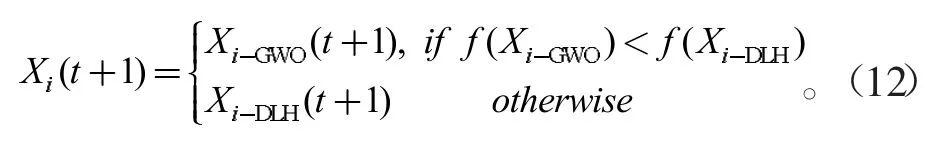
所有灰狼个体完成位置更新后,迭代计数器加1,直到达到预先设定的迭代次数。
2.3 基于I-GWO优化BP神经网络
若误差函数存在多个峰值,BP神经网络沿着负梯度方向寻找最优解的过程中易陷入局部极小点,预测结果产生的偏差较大。然而,I-GWO算法的全局搜索能力较强,可以为神经网络寻找出全局最优解。使用BP神经网络的误差函数作为I-GWO算法的适应度函数,通过BP神经网络连接权值和阈值的数量来决定I-GWO算法中灰狼的维数,那么I-GWO算法寻优的过程就是权值和阈值更新的过程。因此,I-GWO算法寻优的过程替代了BP神经网络梯度下降的过程[17]。经过不断更新和迭代,最终确定出全局最优值,即灰狼α所处的位置。最后将灰狼α的位置映射为BP神经网络的权值和阈值,并结合BP神经网络公式对样本数据进行拟合和预测。改进灰狼算法优化BP神经网络的算法过程如下。
步骤1:确定神经网络的节点数量和激活函数,适应度函数选用均方误差(Mean Square Error,MSE)。
步骤2:确定初始化参数。包括灰狼的维数、参数的上下界、灰狼的种群数量及最大的迭代次数。
步骤3:初始化灰狼位置。将N只灰狼随机的分布到搜索空间,并计算每只灰狼的适应度。
步骤4:选取出适应度最佳的3只灰狼α,β和δ。根据式(7)计算出第一个候选位置Xi-GWO(t+1),并更新参数A,C和a。
步骤5:根据式(9)计算出邻域的半径Ri(t),并构建Ni(t)的邻域矩阵。
步骤6:根据式(11)计算另一个候选更新位置Xi-DLH,d(t+1),并判断每一维度是否存在越界行为。
步骤7:比较Xi-GWO(t+1)与Xi-DLH,d(t+1)的适应度值,选出最优的候选位置。如果所选择的最佳候选位置劣于Xi(t),则Xi(t)作为最佳候选位置。
步骤8:判断是否达到最大迭代次数,若是算法结束,否则执行步骤4到步骤7。
步骤9:将最优解的位置映射为神经网络的权值和阈值,并输入到神经网络的公式中进行拟合与预测。
3 实例分析
3.1 数据选取
样本数据源于“广联达造价指标网”和“郑州市建设信息网”,共收集了31组2013—2019年之间河南地区住宅工程造价数据。由于各地区经济发展水平的不同和编制时间的差异,以河南省郑州市2019年第一季度造价指标作为基准,对31组单方造价指标进行比例换算。河南省住宅工程造价部分数据见表2。
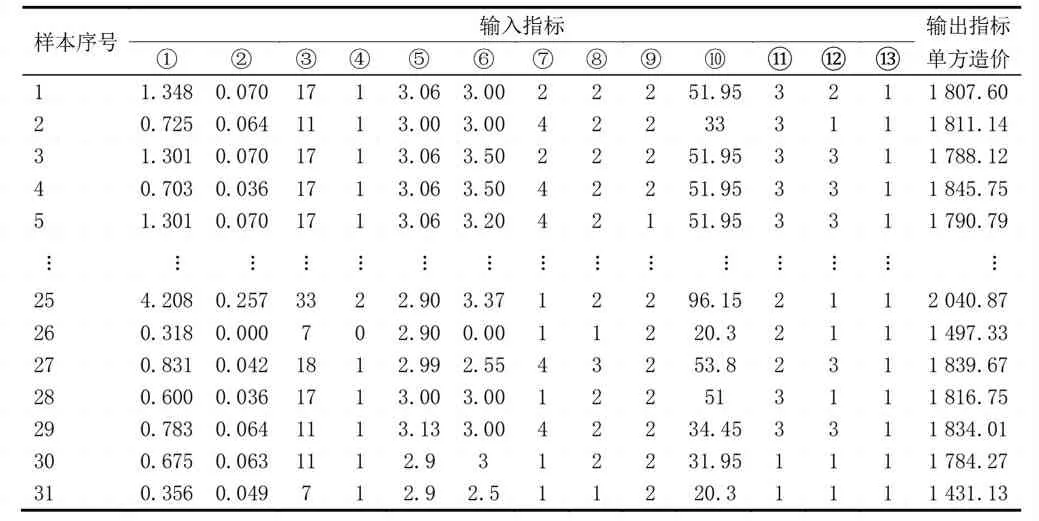
表2 河南省住宅工程造价数据(部分)
3.2 主成分分析
由于各工程造价指标的量纲不同,并且数量级差距过大。在主成分分析之前,需要对31组造价数据进行标准化处理。本文采用标准分数法(Z-SCORE)对原始数据进行标准化操作,并将处理好的数据导入SPSS中进行主成分分析。各主成分的方差百分比与累计贡献率见表3。
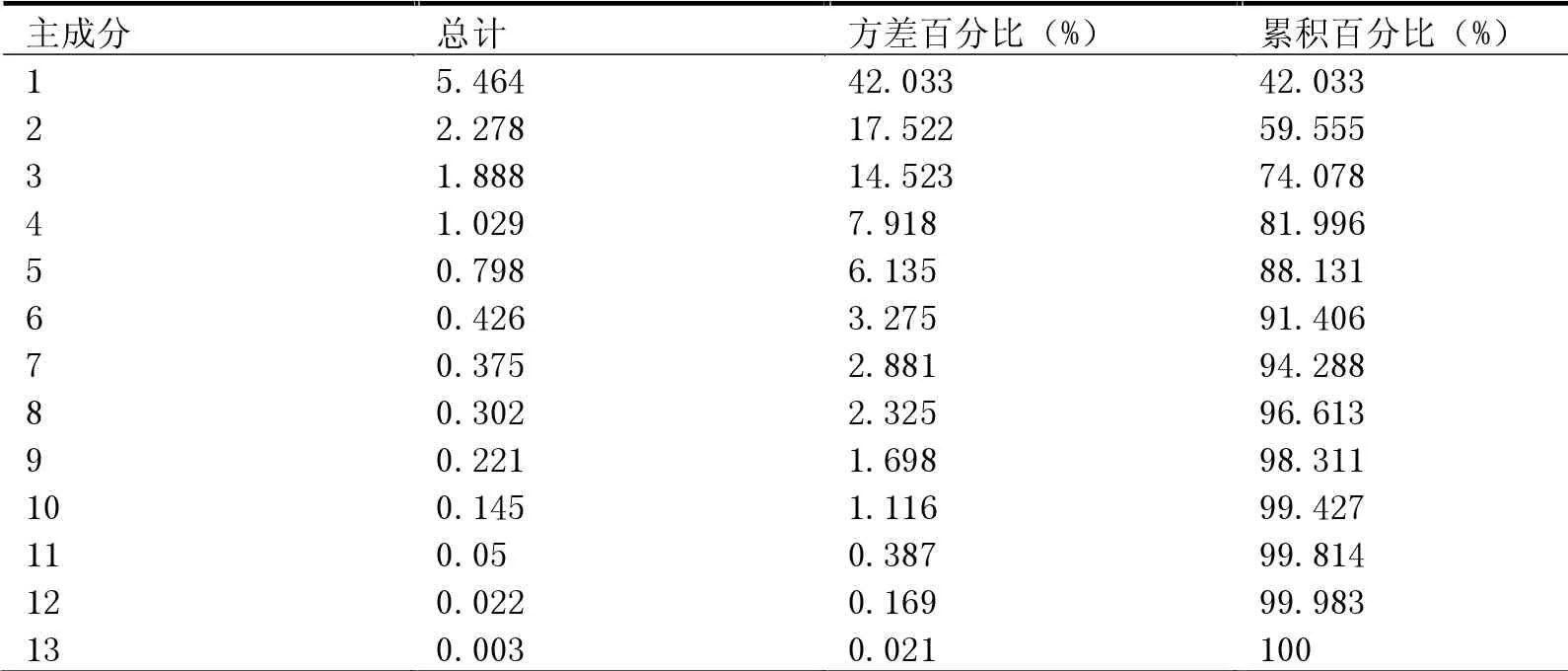
表3 方差百分比与累计贡献率
样本数据KMO为0.65大于要求的0.5,并且巴特利特显著性为0,证明该组数据适合进行主成分分析。本文选取前7个累积贡献率达94.29%的主成分作为预测模型的输入集,并进行训练与仿真。
3.3 模型的训练与仿真
选择河南省造价数据集前24组作为训练样本,剩余7组作为检验样本。I-GWO算法的参数设置如下:算法初始化边界范围为[-3,3],灰狼个数N=150,最大的迭代次数为1 000次。BP神经网络采用7-7-1的拓扑结构,使用sigmoid作为激活函数。同时,通过多模型对比分析,验证I-GWO-BP模型的有效性。其中GWO算法的参数设置与I-GWO算法保持相同,PSO算法的参数设置如下:惯性权重w采用线性递减的策略wmax=0.9,wmin=0.5,学习因子c1=c2=2,粒子个数N=100,最大训练次数为1 000次。传统BP神经网络、粒子群算法、传统灰狼算法与改进灰狼算法的预测结果对比如图1所示。算法的误差曲线如图2所示。
由图1可知,BP神经网络的预测误差最大,贴合度最差。同时在算法执行的过程中发现神经网络具有较强的随机性,需要多次训练才能达成满意的结果,预测稳定性最差。随着优化算法的加入,预测结果准确度和稳定性有了很大的改善。其中I-GWO算法的预测结果与真实结果最为贴近,在贴合度和预测准确性上要优于其他算法。

图1 不同算法预测结果对比
从图2可知,PSO算法误差曲线下降缓慢,并经过一段时间的迭代后误差停止减少,训练误差最大。其原因是在PSO算法寻优的过程中陷入了局部极小点,同时PSO算法也无法从中脱困,导致了预测的准确度较差。GWO算法前期收敛速度较慢,随着迭代次数的增加误差仍然可以继续降低,最后也可以达到理想的误差精度。I-GWO算法误差曲线下降速度最快,误差的精度较高,说明该算法的全局寻优能力较强。

图2 不同算法误差曲线对比
3.4 预测结果分析
本文使用平均误差Mean、均方根误差RMSE、拟合优度对各预测模型进行评价。各算法运行20次,并选取各评价结果的均值进行对比,结果见表4。
由表4可以看出I-GWO算法的预测模型要明显优于其他算法,I-GWO算法的均方根误差最小,平均误差最小,拟合优度最大,说明该模型预测的准确度较高。I-GWO-BP模型的最大均方根误差为67.89元/m2,最小均方根误差为53.17元/m2。同时I-GWO-BP模型最大相对误差为3.48%,最小相对误差为2.63%,其预测误差满足可行性研究阶段10%的误差要求。IGWO-BP预测模型在住宅工程的造价预测中具有实际的现实意义。

表4 不同模型预测结果对比
4 结束语
本文采用I-GWO-BP模型对住宅工程造价进行预测,有以下结论:
(1)I-GWO-BP模型可以对中高层、高层和超高层住宅的工程造价做出很好的区分,并根据建筑的特点和往年的造价数据实现了住宅工程的造价预测。
(2)采用主成分分析法筛选工程造价指标,选取出7个累计贡献率为94.29%的造价指标,简化了输入数据,提高预测准确度。
(3)使用I-GWO算法代替BP神经网络梯度下降的过程,增强了神经网络的全局搜索能力,预测结果更加准确。I-GWO-BP模型预测结果满足可行性研究阶段的误差要求,可以作为房地产估价师的辅助工具。

