基于WOA- VMD 的桥梁监测挠度数据处理方法

黄惠娟，颜全胜＊

（华南理工大学土木与交通学院，广东广州 510641）

引言

在斜拉桥结构中，挠度的温度效应影响较大，车辆、风荷载引起的挠度不显著，如何有效地分离挠度数据中温度造成的影响，是准确分析随机荷载下桥梁状态的关键问题之一。若采用固定的滤波器及设定的阈值方法分解，对长期的桥梁挠度数据适应性不强。小波变换[1]基函数以及阈值参数的选择存在无通用性规则，随机性较大的问题，VMD[2-4]的分解层数K 和惩罚因子α 选取范围有限。无需设定参数及基函数的分解方法，如EMD[5]及其改进算法，集合经验模态分解、完全集合经验模态分解、完全噪声辅助聚合经验模态分解，皆存在模态混叠、结果随机性问题。

相比EMD 及其改进方法，VMD 分解的数据具有较好的鲁棒性。为实现VMD 自适应数据分解，采用鲸鱼优化算法选择参数K 和α 的取值。鲸鱼优化算法能在两参数取值范围内，以随机或螺旋收缩的方式可逐步逼近参数的最优组合。因此，提出WOA-VMD 方法，以功率谱熵最小作为鲸鱼优化算法的适应度函数，实现自适应桥梁监测挠度数据选取VMD 关键参数。

1 基于WOA-VMD 的挠度温度效应分离原理

1.1 VMD 原理

VMD 摒弃了EMD 中模态分量的循环筛选过程，具有较好的抗噪能力。该方法将原始信号分解为K 个本征模态函数（Intrinsic Mode Function，简称IMF），通过惩罚因子α 使得各个IMF 之和与原始信号的约束变分最小，约束变分模型见公式(1)。

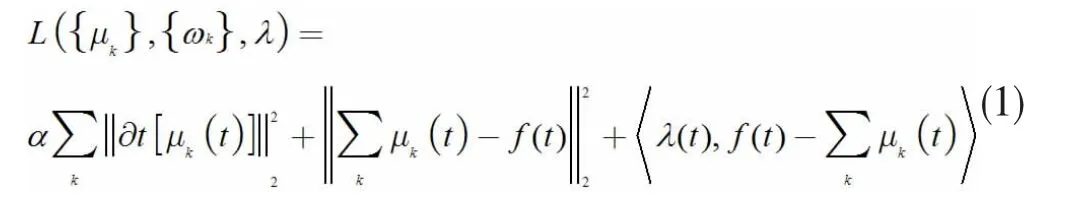
主要利用交替方向乘子法根据公式(1)推导出每个IMF 频域的更新公式(2)，最终收敛得到K 个中心频率为{ωk}的模态分量{μk}。

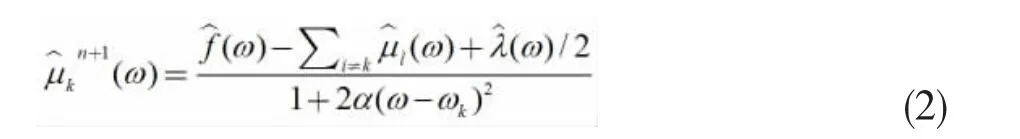
VMD 方法对原始数据分解的效果会受到参数K和α 的影响。因此，需同时考虑两参数选取，找到最优参数组合。通常分解层数K 达到8 层已经可充分挖掘数据的潜在有效信息，K 的试算区间设置为[2，8]，根据文献[4]将α 的试算区间设置为[1000,5000]。

1.2 基于WOA 及功率谱熵的最优参数选择

为从原始信号分离温度引起的挠度，以重构信号的功率谱熵最小作为WOA[6]适应度函数，找到VMD的最优参数K 和α。搜寻流程如下：

（1） WOA 参数初始化。将鲸鱼位置输入至VMD算法分解原始信号，依据公式(3)、(4)计算功率谱熵值H，式中μk（ω）为各IMF 的频域函数，L 为信号长度。

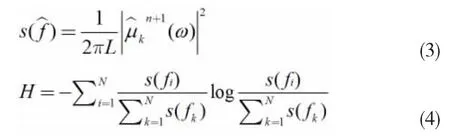
（2） 位置更新。鲸鱼在搜索猎物时具有一定的随机性，当系数|A|≥1 时，说明鲸鱼处于收缩圈外，选择随机方式更新位置；随机更新位置公式如下：

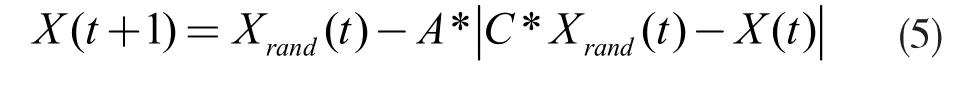
|A|＜1 表示鲸鱼在收缩包围圈内，当p＜0.5 时依据公式(6)旋转搜寻；P＜0.5 时鲸鱼群收缩包围，位置更新见公式(7)。

（3） 遵循WOA 算法的随机螺旋环绕机制，输出最优解得参数K 和α。

1.3 基于WOA-VMD 方法的信号温度效应提取流程

综合应用WOA 和VMD 能实现自适应桥梁挠度量测数据分解，达到数据提取温度效应目的。首先，输入原始信号至WOA-VMD算法中，依据随机生成的鲸鱼位置，计算VMD 重构数据的功率谱熵。在迭代的过程中，鲸鱼群按照随机螺旋收缩运动方式，向功率谱熵值最小的方向运动，最终获取参数K和α 的最优组合。

其次，依据参数最优组合，将原始数据分解为K 个IMF，计算每个IMF 的功率谱熵，得到有效分量范围，并计算其信息增益值。信息增益值[7]（Information Gain，IG）越大，表示与原始数据的相关程度越紧密。在斜拉桥结构响应的长期监测中，温度效应分量与挠度数据相关程度大于其他因素效应分量，选取信息增益值大的分量作为挠度的温度效应。信息增益计算见公式(8)。

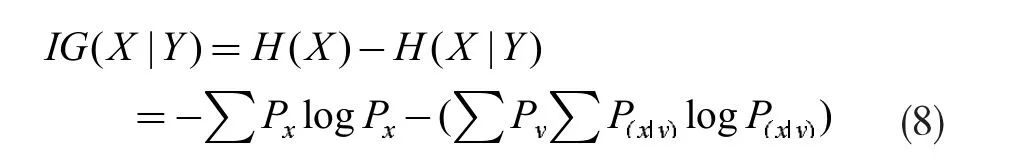
2 数值模拟信号分析

为了验证WOA-VMD 算法数据分解能力，设计了仿真信号模拟桥梁挠度数据。在自适应数据分解的算法中，完全噪声辅助聚合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis，CEEMDAN）比其他算法预测性能好。因此，对比CEEMDAN 与WOA-VMD 的分解结果，验证本文算法特征提取能力更加有效和可靠。

2.1 仿真信号概况

假设日温差引起的挠度f1=9.48sin（πt/12），年温差挠度表达是f2=33sin（πt/4380）。此外，叠加10 信噪比的高斯白噪声fN，输入数据表达式为f（t）=f1+f2+fN，其中t 为时间，每隔1 h 采样一次，采集的时长为2 500 h。f（t）各分量时域及对应的频谱见图1。

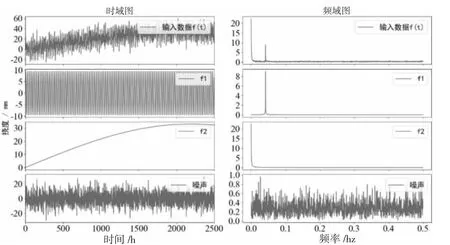
图1 10dB 信噪比仿真数据

2.2 比较温度效应的拟合效果

分别采用WOA-VMD 与CEEMDAN 仿真数据分解，各分量的频域见图2。

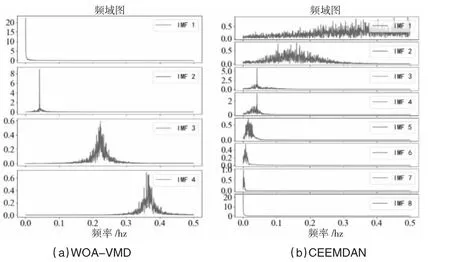
图2 分解层IMFs

WOA-VMD 重构数据有4 个分量，CEEMDAN 的重构数据中有8 个分量，计算有效分量的信息增益值，WOA-VMD 分解的IMF2 和IMF1 分量对应原始数据的f1和f2分量。CEEMDAN 的IMF3 与IMF4 的主要频率对应原始数据的f1分量，IMF8 分量为原始数据f2分量的重构数据。

两方法的重构的温度效应分量f1和f2与原始数据的日、年温差效应的均方根误差见表1，结果显示WOA-VMD 重构的日温差效应拟合精度相较于CEEMDAN 算法提升了56.35%，重构的年温差效应拟合精度相较于CEEMDAN 算法提升了24.48%。

表1 重构数据分量与原始数据分量均方根误差

3 工程实例分析

3.1 工程概况

洛溪大桥拓宽工程为双塔双索面叠合梁斜拉桥，该桥2022 年3 月1 日至2022 年3 月7 日的左幅和右幅主跨跨中挠度数据见图3。应用WOA-VMD 和CEEMDAN 对挠度数据分析，验证前者在实际工程中分离挠度温度效应的有效性与可靠性。年温差效应时间的跨度较长且缓慢，在短时间内的年温差效应幅值远小于日温差效应幅值，7 天的挠度数据中仅分离出日温差效应。

图3 洛溪大桥主跨跨中挠度数据

3.2 实测挠度数据处理

WOA-VMD 依据挠度数据特征，得出K=5 和α=3 670 为VMD 的最优参数组合。VMD 将挠度数据分解为5 个IMF，计算各IMF 的功率谱熵，推出噪声与信号的分界分量为IMF4，即IMF5 分量判定为噪声，各分量之间的频率无混叠现象。CEEMDAN 将挠度数据分解为16 个IMF，计算各IMF 的功率谱熵，IMF1 至IMF11 分量判定为噪声，各分量之间的频率存在混叠现象。计算两方法分解左右幅主跨跨中挠度数据的非噪声分量信息增益值，选取信息增益值大的分量为日温差。WOA-VMD 左右幅提取的日温差挠度效应为IMF1，CEEMDAN 提取的左幅日温差效应为IMF13 至IMF16 的组合分量，右幅日温差效应为IMF14 至IMF16 的组合分量。

洛溪大桥左右两幅主梁结构温度，采用上述两种方法分离出的主梁跨中挠度温度效应见图4。采用温度挠度效应与结构温度的相关系数，验证方法的有效性。WOA-VMD 分离的左右两幅主跨跨中挠度温度效应与结构温度的相关系数分别为0.9313 和0.8716，CEEMDAN 分离的挠度温度效应与结构温度的相关系数分别为0.8674 和0.8242。因此，WOA-VMD 提取的左右两幅挠度日温差效应与结构温度相关性较CEEMDAN 均有所提高。

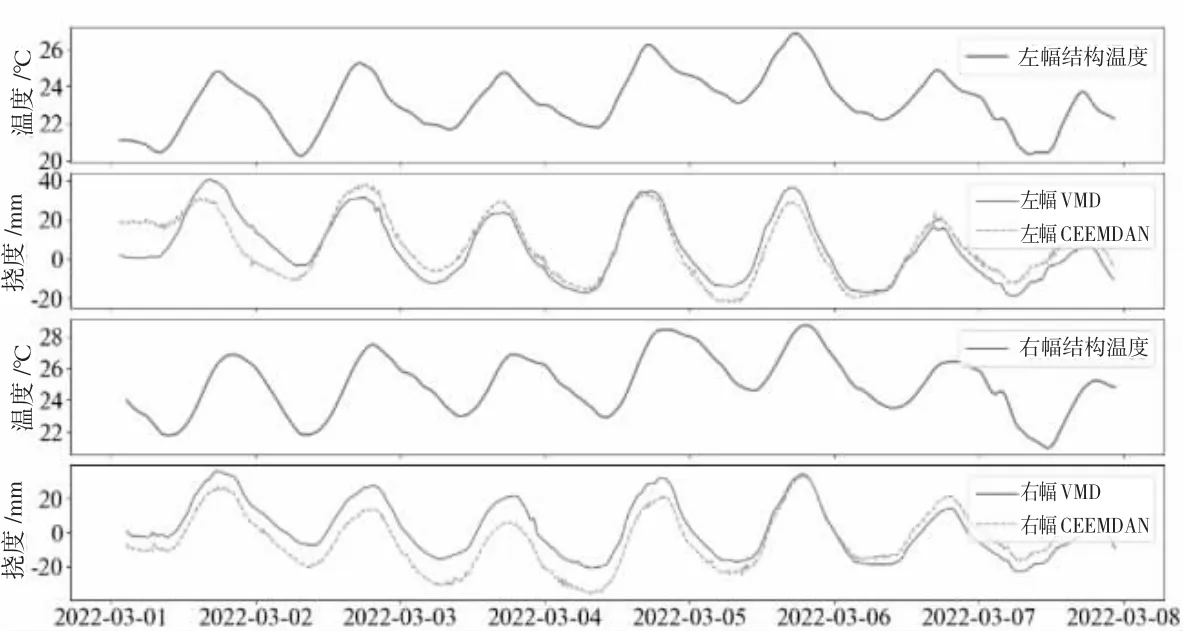
图4 主跨跨中挠度结构温度及分离的温度效应

4 结论

为实现桥梁监测数据实时温度效应分解，提出了自适应信号变化的数据处理方法WOA-VMD。结合工程实例得出以下结论：

（1） WOA-VMD 通过功率谱熵作为鲸鱼优化算法的适应度函数，能自适应数据特征选取VMD 关键参数，充分发挥VMD 数据处理的鲁棒性及抗噪能力。

（2） WOA-VMD 分解了桥梁监测挠度数据，低频IMF 的信息增益值最大，由于在斜拉桥中温度是引起挠度的主要因素，可认为该分量为挠度的温度效应。与CEEMDAN 相比，分离实测的左右两幅桥梁主跨跨中挠度温度效应与结构温度相关性提升了7.37%和5.72%，为后续车辆和风荷载效应的随机性分析提供了有效的数据处理方法。