下凡的精灵:投影向量*
——对投影向量的教学建议
⦿广州市番禺区石北中学 广东省吴和贵名教师工作室 姜宝松
1 问题的产生
《普通高中数学课程标准(2017版)》实施后,2019年人教版《普通高中教科书·数学·必修·第二册》(后简称“新教材”)中出现了概念“投影向量”,取消了旧教材中“向量的投影”这一概念.有教师在讲授这一知识时误认为还是旧的概念,还有教师发现投影向量,只是在证明数量积的分配律时使用过,后面就如昙花一现般消失不见,不理解教材中为什么引入投影向量.
2 概念辨别
旧教材中向量的投影是一个数量,利用这个数量来解释向量的数量积.有教师因为旧教材的教学经验,先入为主地认为投影向量也是个数量,从而造成概念混淆.

图1
3 投影向量的数学本质及其作用

3.1 勾股定理

图2

3.2 点到直线的距离(向量推导)
设平面直角坐标系内点Q(x0,y0),直线l:Ax+By+C=0,求点Q到直线l的距离d.

图3
推导:如图3,在直线l上任取点P(x1,y1),则有Ax1+By1+C=0.


3.3 点到平面的距离公式

图4

同理,也可用投影向量得出两异面直线间距离公式.
以上距离公式的推导过程,可以总结为:点到平面的距离,即是向量(点和平面内的任意一点形成)在平面法向量上的投影向量的模;点到直线的距离亦是如此.这一过程体现了投影向量在降维中的作用,投影向量就像是高维空间降到低维子空间的精灵,联结起高维空间与低维子空间,舞动穿插于诸多数学知识中.
4 投影向量的教学建议
新教材中,在数量积的定义之后,给出了投影和投影向量的概念,并用较大篇幅探讨明了投影向量的计算方法.教材至此对投影向量停止介绍,之后仅在数量积的分配律时使用过投影向量,在后续教材中不见踪迹.这也是部分教师对投影向量地位认识不足,对教材中投影向量感到突兀的原因.结合上述投影向量的本质和作用,给出如下教学建议.
4.1 投影向量计算方法的改进
还可利用向量的代数特性,进一步推导出投影向量计算方法的另一种形式:
即投影向量的计算方法有两中形式:

形式(1)体现出投影向量运算的几何特征,形式(2)体现出投影向量的代数运算特征.由形式(2)还可以推导投影向量的模,推导如下:

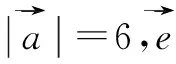


图5
例1、例2均为教材中的原题,借助几何直观,利用形式(1)可迅速求解.




例3、例4以及2019年人教版数学必修第二册第89页第15题,用形式(2)容易解决.
4.2 利用投影向量解释数量积

下面为几何解释,如图6所示:

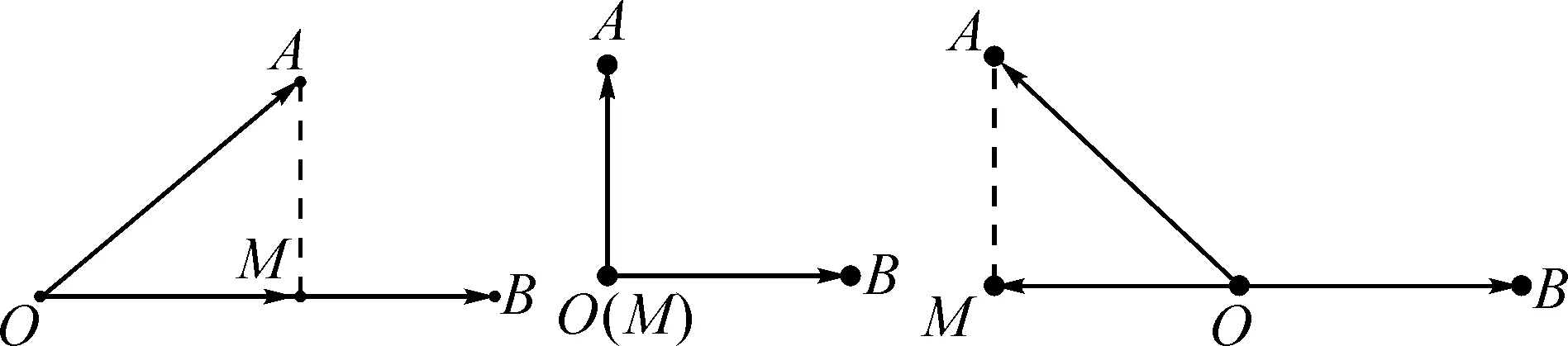
图6


图7




图8
例5、例6均可利用投影向量巧妙解答.用投影向量解释数量积,在常用数量积计算方法上进行了补充,有助于学生直观想象素养的提升,也能帮助学生进一步理解向量运算.
5 结束语
向量是沟通代数与几何的桥梁,投影向量则把高维空间和低维子空间进行了联结,像是高维空间“下凡”到低维空间的数学精灵.笔者认为,教师在讲授新课时若能增加课时补充这一内容,或是新教材中补充用投影向量来解释数量积运算的内容,可以更深入揭示向量数量积的运算本质,让投影向量的作用体现得更加灵动.

