微米颗粒衍射成像过程仿真与特征分析
王文进,方 敬,杨 翔,向 理,田 芃,胡新华
(1. 湖南理工学院 信息光子学与空间光通信湖南省重点实验室,湖南 岳阳 414006;2. 湖南理工学院 物理与电子科学学院,湖南 岳阳 414006;3. 东卡罗莱纳大学 物理系,美国 北卡罗莱纳州 27858)
相干散射光强度的空间分布即衍射图像与散射体的形态和折射率分布高度相关,所以基于散射光成像理论的检测技术被广泛应用于生物、大气、海洋科学等领域[1,2]. 近年来,Yu[3~5]等人开发出一种可以同时获得散射体在不同偏振方向上的衍射图的衍射成像式流式细胞仪,如图1 所示. 入射线偏振光被流体室中的微粒散射后进入数值孔径为0.55 的显微物镜,然后经过镜筒透镜成像于CCD 传感器上. 通过分析衍射图像特征可以实现包括生物细胞在内的不同结构散射体的区分和结构参数变化分析[6~8]. 但如何利用理论模型对微粒散射光衍射成像过程进行快速、准确分析还没有很好地解决[9]. 目前研究相干光传输成像的主要方法是计算麦克斯韦方程组或求解波动方程,求解复杂且误差大[10]. 所以必须建立一个快速、精确的理论仿真模型获得微粒的衍射图像并对衍射图像的纹理特征进行提取、分析[11]. 图像纹理特征提取、分析的方法有很多,其中灰度共生矩阵(GLCM)被证明是一种非常有效的手段[12].
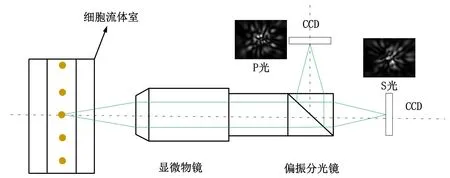
图1 偏振衍射成像式流式细胞仪
本文基于严格的光散射模型获得了由微球、微圆柱、微椭球组成的1965 个复杂散射体在流体室和显微物镜之间的光强分布,并利用高斯混合模型(GMM)对图像的GLCM参数进行了聚类分析,同时研究了散射体结构参数与GLCM 参数之间的关联.
1 研究方法
散射体在流体聚焦作用下依次流进流体室. 当散射体经过入射激光的聚焦区域时会产生相干的散射光,散射光经过主介质和玻璃以后进入成像单元,如图2 所示.

图2 微粒衍射成像过程仿真
首先,定义散射体三维空间内任一点的折射率
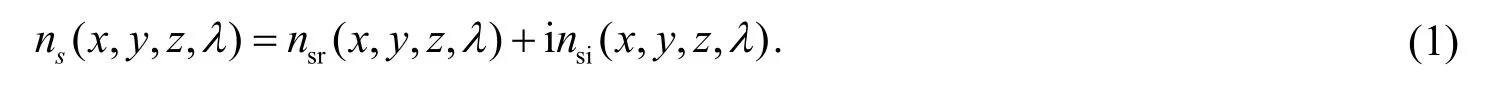
其中nsr为折射率的实部决定散射体的散射系数;nsi为折射率的虚部决定散射体的吸收系数;λ为入射光的波长.
通过这种方式可以实现任意结构、非均匀散射体光学模型的建立. 然后,基于离散偶极子近似理论(ADDA),计算强度为Ii的平行激光入射时空间任意点的光强
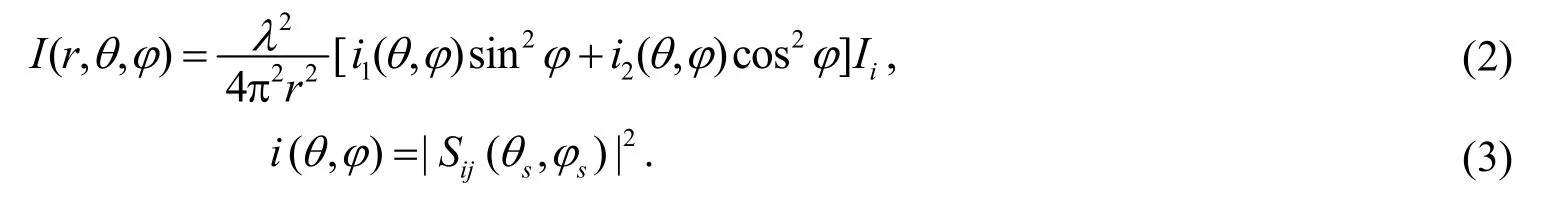
其中i1(θ,φ)与i2(θ,φ)分别为与偏振方向平行和垂直散射面的散射强度函数;r为空间任意一点距离散射中心的距离;S ij(θs,φs)为微粒的散射振幅函数即穆勒矩阵,这里i、j分别取值为1、2、3、4;θ、φ为散射光线的散射角和方位角.
通过矩阵元的不同组合运算可以实现任意偏振光散射问题的求解,以入射光偏振方向为45°时S 偏振方向的成像为例,有
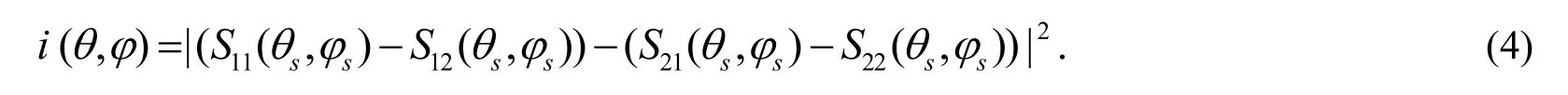
最后,利用MATLAB 程序将I(r,θ,φ)投射到入射平面Γin上,Γin位于流体室内是虚拟平面. 入射平面上的光强分布由具有一定尺寸和像素分布的图像表示,传播方向由(θs,φs)确定. ZEMAX 基于成像单元模型,利用几何光学的方法分析散射光经显微物镜系统后的光强分布.
图3 为直径1~9.5 μm 的微球颗粒的实验和仿真图像,通过对比可以看出两者基本一致. 在文[3]的研究中,通过仿真模型对单球微粒的直径分布进行了分析,其结果与本实验结果以及聚乙烯微球供应商提供的数据高度吻合,由此证实了模型的可靠性.

图3 仿真模型的实验验证(A)和图像特征分析(B)
获得衍射图像之后,GLCM 被用于图像纹理特征的提取和分析. 通过GLCM 可以获得与图像相关的16 个参数,每一个参数都具有不同的统计意义,但相互之间也具有一定的相关性. 根据GLCM 参数之间的斯皮尔曼相关系数(大于0.85),可以将16 个参数分为六组,见表1. 结合微粒光散射原理,同一组参数都对应散射体类似的形态特征. 所以,本文分别从六组参数中选取角二阶矩(ASM)、熵(ENT)、对比度(CON)、相关性(COR)、协方差(VAR)、逆矩差(IDM)、和熵(SEN)等7 个参数对衍射图像的纹理特征进行了研究.

表1 GLCM 参数分组结果
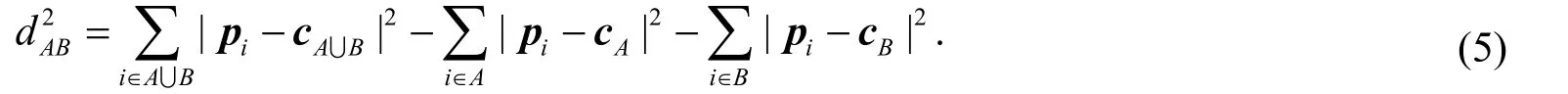
其中pi和c分别是散射体和不同分类集合在GLCM 空间内的位置向量和中心.
2 仿真分析
2.1 复杂散射体聚类
散射体形态结构见表2. 表2 中共有1965 个散射体,每个散射体都是由单个或两个基本单元按照不同排列方式组成. 基本组成单元有球、圆柱、椭球三种不同形状,每种基本组成单元包括1.558 和1.4 两种不同折射率. 图4 为基本组成单元不同的散射体的主要衍射特征. 由于基本组成单元的折射率是均匀的,所以三者的衍射图像特征类似,都是以条纹状和网格状为主. 但是衍射图像特征之间也有差别,这是由散射体之间结构的差异所引起的.

图4 不同组成单元散射体的衍射条纹特征

表2 散射体形态结构
利用GLCM 参数可以将衍射图像纹理反应出来的散射体特征进行量化研究. 表2 中所有散射体的衍射图像首先归一化为8 位图像,然后沿水平、竖直、主对角线、副对角线四个方向提取每一张衍射图像的GLCM 参数并计算平均值,以用于散射体聚类和结构特征研究. 表2 中的所有散射体、折射率为1.558 的散射体、折射率为1.4 的散射体按照基本组成单元进行无监督聚类,结果见表3.

表3 散射体聚类结果
从表3 中可以看出,当散射体中包括折射率变化时,平均准确率为65.8%. 这主要是因为球和椭球组成的散射体以及圆柱和椭球组成的散射体之间有一部分没有准确聚类. 当散射体的折射率为1.558 时,聚类准确率可达到95.7%; 当散射体的折射率为1.4 时,聚类准确率为90.5%. 虽然折射率为1.4 的散射体数量不多,其聚类结果不具有统计意义,但是可以看出折射率的变化对聚类结果有明显的影响. 这说明当散射体折射率均匀时,利用GLCM 参数可以有效分析散射体几何结构变化对衍射特征的影响.
2.2 散射体结构参数与GLCM 参数定量关联
研究表明单微球尺寸变化与衍射图像特征之间具有定量关联[11]. 本文以双圆柱模型为例,研究复杂散射体与其衍射特征之间的关系. 双圆柱的主要参数包括中心间距、中心连线与z轴方向之间的夹角. 图5所示为双圆柱中心连线沿z轴方向,中心间距在3.1~6 μm之间变化时衍射图像特征参数CON的变化. 图6 所示为双圆柱中心间距为4.5 μm,中心连线方向与z轴夹角从5~175°变化时衍射图像特征参数COR 的变化. 图中圆点为GLCM 参数的实际数值,虚线为拟合的曲线,并给出拟合曲线的数学表达式及拟合优度判定系数R2.
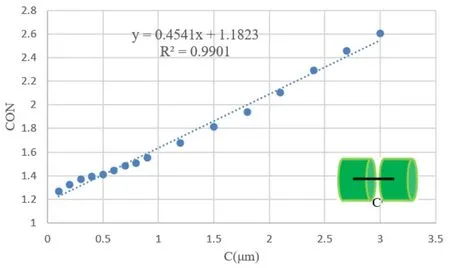
图5 圆柱中心间距离与CON 的线性关系

图6 圆柱中心连线方向与COR 的线性关系
从图5 可以看出,双圆柱中心间距(C)与衍射图像特征参数CON 之间具有定量关联. 当C从3.1 μm 逐渐增加至6 μm 时,CON 也逐渐增加. 此外,CON 随C变化的散点图与趋势直线的拟合优度R2= 0.99,这说明两者具有良好的线性关系. 图6 为双圆柱中心连线方向与z轴夹角(θ)和衍射图像特征参数(COR)之间的定量关联. COR 关于θ= 90°对称,这是因为衍射模型中入射光沿z方向并且双圆柱散射体具有良好的轴对称关系. 另外,图中四次曲线与COR 随θ变化的散点图同样具有良好的拟合关系.
3 结束语
本文基于离散偶极子近似算法,结合光迹追踪软件,对复杂结构散射体的衍射过程进行了快速、精确仿真,得到了不同结构散射体的衍射图像. 并利用衍射图像量化特征实现了散射体的无监督聚类分析,建立衍射图像纹理特征参数与散射体三维结构参数之间的定量关联. 研究表明,衍射图像特征虽然很难用视觉来量化和解释,但是非常适用于微米量级散射体的免标记分类与识别以及结构参数的定量分析.

