波动参数对冷凝液膜传热影响的微观机理研究

张慧杨洛鹏孙志伟杨岩

(1.山东建筑大学 热能工程学院，山东 济南 250101；2.山东理工大学 电气与电子工程学院，山东 淄博 255000；3.美的集团股份有限公司，广东 佛山 528000)

0 引言

冷凝传热是一种高效的能量传递方式，已在石油化工、制冷、航空航天和海水淡化等工业领域得到了广泛应用。冷凝液膜的波动过程中蕴含着丰富的动力学特性，同时液膜的波动对传热、传质的强化作用在换热过程中得到了广泛应用[1-2]。

对波动液膜的实验研究主要集中在流动和传热特性两个方面。液膜厚度和膜内速度分布是影响液膜流动形态和传热特性的重要参数。WANG等[3]利用近红外线吸收与衰减技术测量了波动液膜的波速，指出波动液膜波速随压力的增加而增加。MARKIDES等[4]通过红外热成像法和平面激光诱导荧光法测量了液膜厚度和壁面温度，发现大雷诺数Re下局部传热系数不再与膜厚成负相关关系，而与壁面温度成正相关关系。ÅKESJÖ等[5]发现在入口处添加多频扰动有助于波动液膜的形成，惯性力、剪切力和表面张力是影响波动的重要因素。张雷刚[6]通过不同重力条件下蒸气在肋板表面的冷凝实验分析了重力对液膜分布和冷凝传热的影响。

波动液膜实验研究取得了较大进展，但由于实验结果的准确性严格受制于实验条件，已测量的速度分布数据多为无相变过程的时均值，缺少详尽的波动冷凝液膜内瞬时速度分布的实验数据，液膜内动力学特性强化传热机理尚未得到充分的研究。采用数值模拟方法可以有效解决实验测量的时滞性与复杂液膜波动过程的不统一。AKTERSHEV等[7]扩展了积分边界层模型，分析了液膜流动过程中的非线性界面运动和传热过程。赵婵[8]对竖直圆管中液膜的波动特征和恒壁温下的传热进行了详细的数值模拟研究。王后全[9]通过数值模拟研究了层流膜状冷凝液膜的波动发展以及由波动引起的强化传热机制。杨丽等[10]采用数值模拟方法研究了不同条件下液膜的流动状态和厚度。邱庆刚等[11]运用流体体积函数法研究了液膜的波动特征、液膜流动方向的速度变化以及液体雷诺数对液膜波动的影响规律。波动冷凝液膜流动数值模拟的研究仅表明界面波动具有强化传热的作用，缺少波动强化传热微观机理的定量分析。

由于现有的研究缺乏对液膜内动力学特性强化传热机理的分析，因此文章针对等温竖直壁面上二维层流冷凝波动的降液膜流动建立数值模型，采用非正交坐标变换求解不规则波动区域，在顺流方向控制方程添加时均值为零的虚拟体积力以引入扰动，利用改进的压力耦合方程组的半隐式算法研究了扰动频率对液膜的膜厚、波长和波速等波动特性的影响，分析了波动强化传热的微观机理。

1 模型的建立与求解

1.1 物理模型

冷凝液膜流动的波动过程如图1所示，x、y分别为冷凝液膜流动过程中顺流及法线方向的坐标，vx、vy分别为顺流速度和法向速度。水蒸气冷凝液膜在重力、黏性力和表面张力的作用下沿竖直壁面向下流动，由表面光滑的液膜逐渐发展成为波前陡峭、波后平缓的水滴状孤波。

图1 冷凝液膜流动的波动过程图

为研究冷凝液膜在竖直壁面上的波动与传热特性，做出以下假设:

(1)竖直壁面温度为TW，冷凝液膜的温度等于饱和蒸汽的温度TS；

(2)冷凝液膜流动分为层流无波区域和层流波动区域；

(3)蒸汽相对于壁面静止，忽略气液相界面处的切应力。

1.2 数学模型

1.2.1 控制方程

质量方程由式(1)表示为

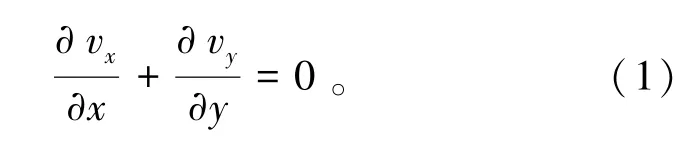
x方向动量方程由式(2)表示为

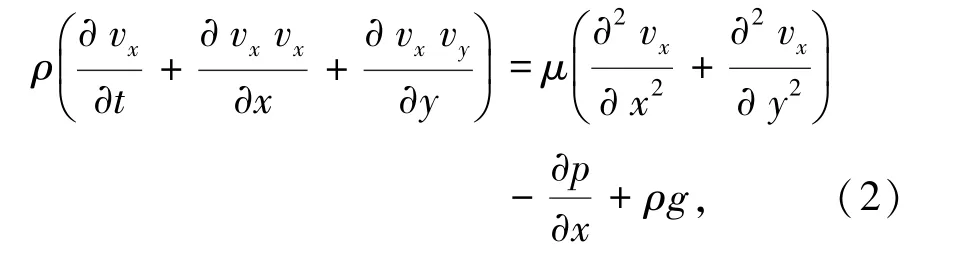
式中ρ为密度，kg/m3；t为流动时长，s；μ为动力黏度，N·s/m2；p为压力，N；g为重力加速度，m/s2。

y方向动量方程由式(3)表示为

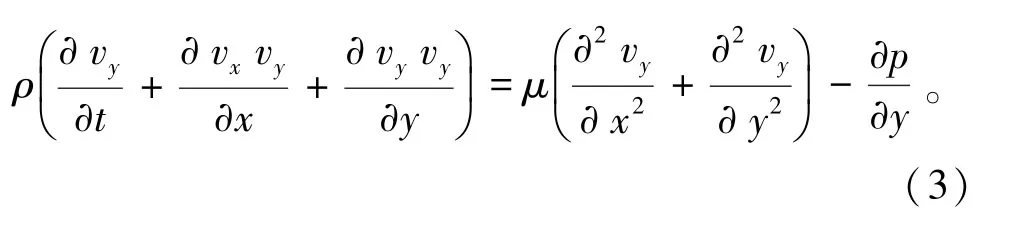
能量方程由式(4)表示为

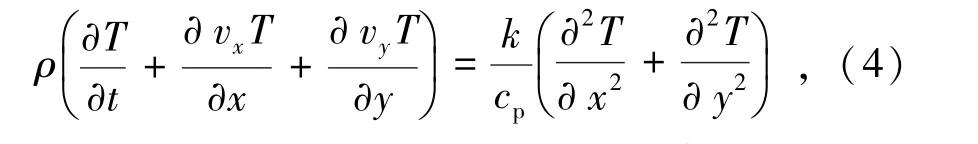
式中T为温度，K；k为导热系数，W/(m2·K)；cp为比热容，J/(kg·K)。

1.2.2 边界条件

壁面处无滑移边界条件由式(5)表示为

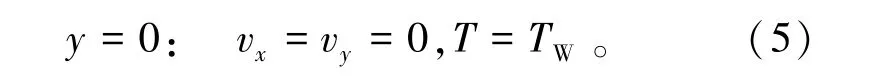
气液界面处边界条件由式(6)表示为

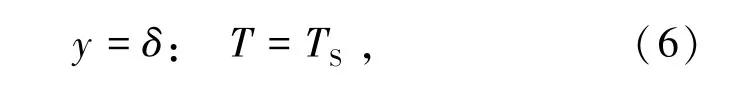
式中δ为液膜厚度，mm。

通过推导气液界面处质量、动量和能量方程，得出气液界面处平衡条件。

质量平衡方程由式(7)表示为

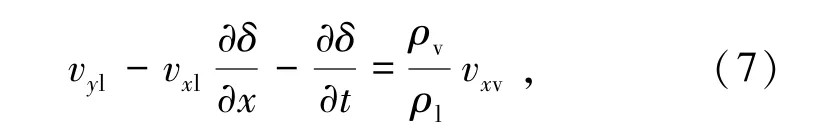
式中vxl、vyl分别为液膜在x、y方向的速度，m/s；ρv、ρl分别为蒸汽、液膜的密度，kg/m3；vxv为蒸汽在x方向的速度，m/s。

切向动量平衡方程由式(8)表示为

式中μl为液膜的动力黏度，N·s/m2。

法向动量平衡方程由式(9)表示为

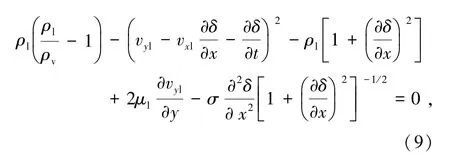
式中σ为表面张力，N/m。

能量平衡方程由式(10)表示为

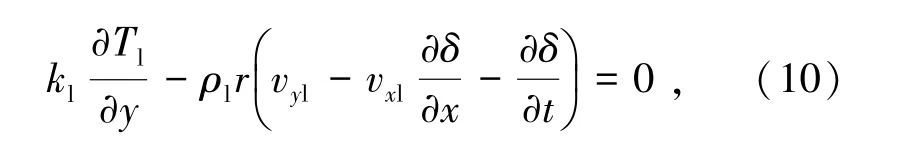
式中kl为液膜的导热系数，W/(m2·K)；Tl为液膜温度，K；r为凝结潜热，J/kg。

1.2.3 坐标转换

模型将欧拉法和拉格朗日法的特点相结合，采用如图2所示的非正交坐标转换法[12]，通过基本关系式、ε＝x(θ、ε分别表示转换后的坐标系，e为单位向量，nL为法向单位向量)将不规则的波动界面转换为矩形区域，从而实现对界面位置的准确捕捉与对控制方程的精确求解。

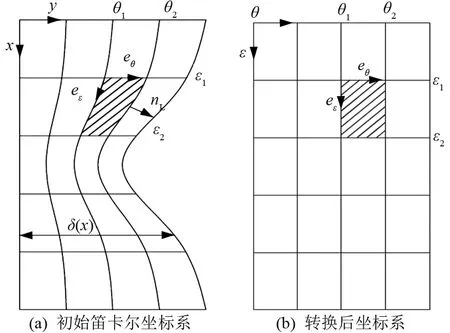
图2 非正交坐标转换示意图

1.3 参数设定

模拟过程中的主要参数设定见表1。

表1 模型参数设定表

在蒸汽冷凝的初始阶段沿液膜流动方向(即x方向)添加一个周期性变化、时均值为零的虚拟体积力作为动量方程的源项，外加强制扰动由式(11)[13]表示为

式中Fv为虚拟体积力，N；φ为扰动振幅系数；f为扰动频率，Hz。

1.4 无关性分析与模型验证

不同网格数量的模型计算得到的平均膜厚分布见表2。当顺流方向网格数＞1207，法线方向网格数＞47时，计算得到的平均膜厚偏差＜1%。综合考虑计算精度和计算时间，选择1207×47的网格划分方法进行计算。

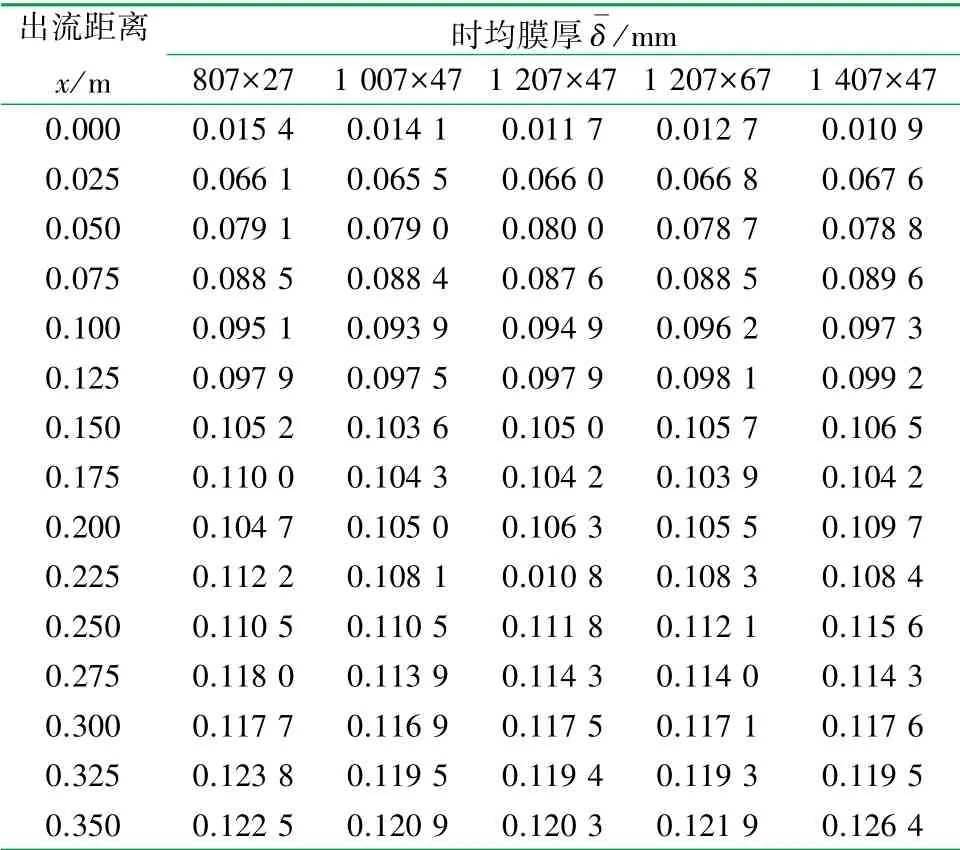
表2 不同网格数下的时均膜厚表

对比16 Hz下非正弦波动峰高和波速的计算结果与NOSOKO实验关联式[14]，如图3所示。在液膜的起始阶段，计算值与实验值相差不大，随着液膜波动峰高的增加，计算得到的波速略大于实验值，两者偏差＜10%，模拟值与实验值较好的一致性验证了计算模型的准确性。产生偏差的原因是NOSOKO实验关联式是基于无相变过程中波动特性参数推导得到的，而文章由于水蒸气的持续冷凝，会推动波动向下游发展，使波速增大。

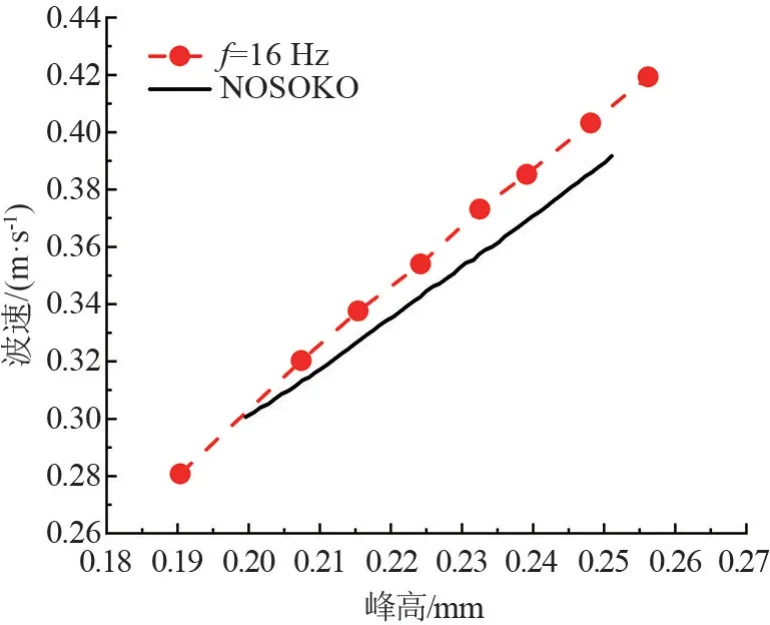
图3 波速与峰高之间的关系图

2 结果与分析

2.1 扰动频率对波动特性的影响

2.1.1 波长

冷凝液膜雷诺数Reδ由式(12)表示为

式中Γ为扩散系数。

不同频率下冷凝液膜的波长随液膜雷诺数的分布如图4所示。由于14 Hz的扰动无法形成振幅连续递增的波动，因此波长随液膜雷诺数的增加呈现分散分布。对于外加＞16 Hz扰动频率的液膜波动，当Reδ＜130时，液膜的波动处于正弦波动区间，波长增加较快；当Reδ＞150时，液膜波动处于非正弦波动区间，波长增速减缓。同一Reδ下，冷凝液膜波长随扰动频率的增加而减小。

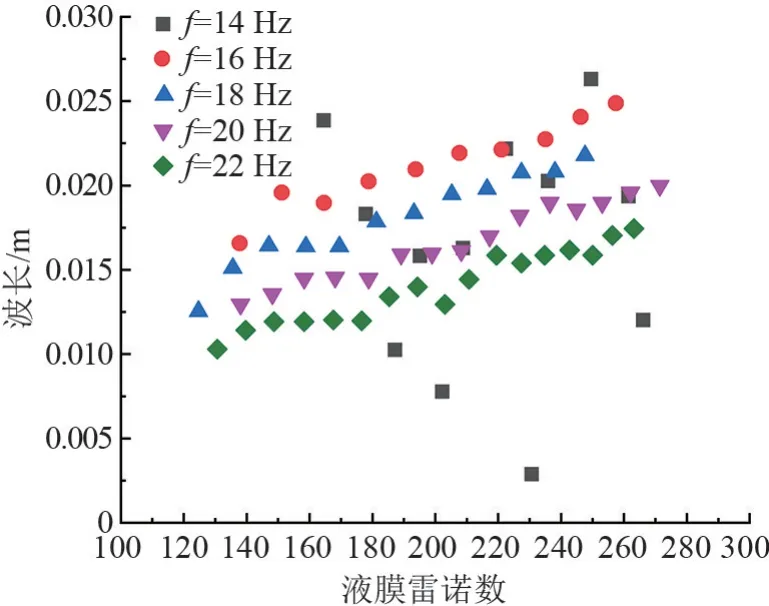
图4 不同扰动频率下的波长分布图

2.1.2 波速

不同频率下冷凝液膜的波速随液膜雷诺数的分布如图5所示。在Reδ＜130的正弦波动区间，计算结果与努塞尔分析解保持一致。130＜Reδ＜150为正弦区域向非正弦区域转变的过渡区域，计算波速明显大于努塞尔分析解。在Reδ＞150的非正弦波动区间，液膜的波速在重力作用下随Reδ近似线性增大，但速度梯度明显小于过渡区域。在非正弦波动区域，16 Hz扰动下的波速大于其他扰动频率。

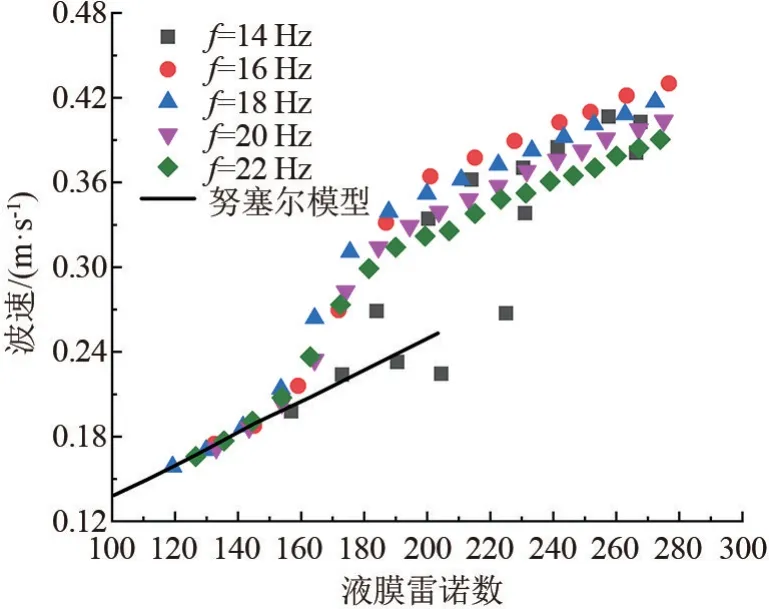
图5 不同扰动频率下的波速分布图

2.2 波动强化传热机理分析

不同扰动频率下无量纲波动界面面积如图6所示。引入无量纲波动界面面积A+＝Awave/A定量分析波动对界面表面积的影响，其中Awave和A分别为波动液膜界面面积和努塞尔光滑液膜表面积。相比努塞尔光滑液膜，波动引起传热面积增加的最大值仅为0.026%，这一结果与文献[15]中波动界面面积较光滑表面增大百分比＜0.03%的结论一致，因此界面传热面积增加是波动强化传热主要因素的结论[16]不适用于冷凝液膜波动。14 Hz扰动下未形成连续发展的非正弦孤波，A+最小；随着扰动频率增大，对液膜面积贡献较大的非正弦孤波波数增多，A+逐渐增大。

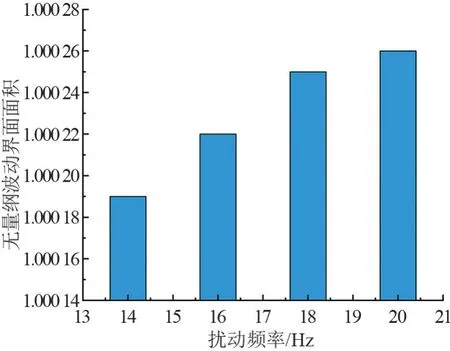
图6 不同扰动频率下的无量纲波动界面面积图

x＝0.3 m处不同扰动频率下的平均传热系数与努塞尔分析解的数量对比见表3。相对于努塞尔分析解，16 Hz扰动下冷凝液膜厚度最小和对流传热系数最大，其中对流作用对强化传热的贡献率为79%，膜厚减少引起的导热作用的贡献率为21%，相对于减薄液膜，对流作用对强化传热起主导作用。

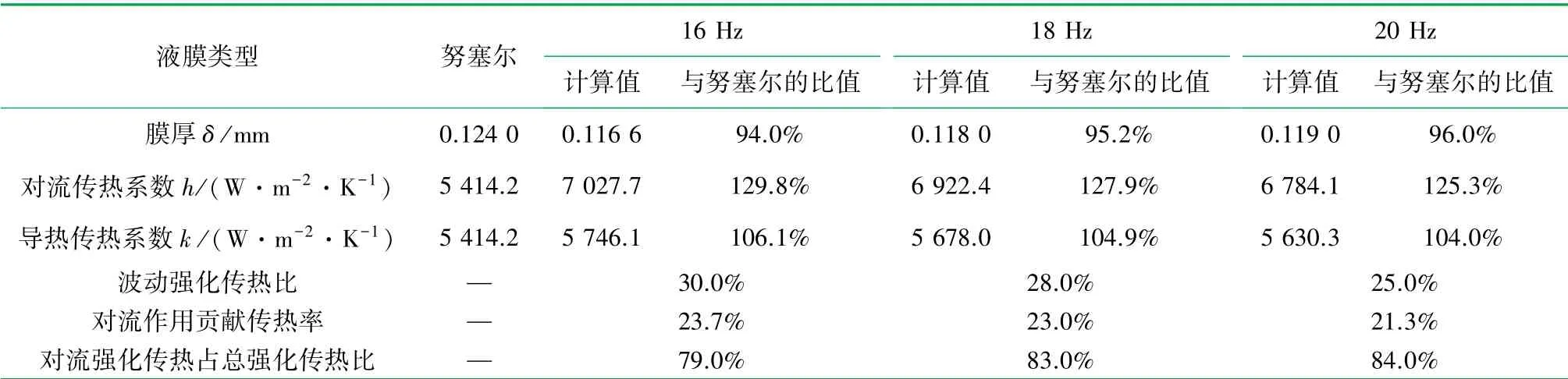
表3 x＝0.3 m处不同扰动频率下传热系数与努塞尔分析解对比表

图4、5证明了16 Hz扰动下的波长和波速在正弦波动和非正弦波动区间都大于其他频率。波长越长，波动对液膜强化传热的作用空间占比越大，波速越大，波动对液膜强化传热的作用频率越高，波长和波速的叠加作用效果使得液膜内的对流作用增强，使得16 Hz扰动下的波动强化传热效果最优。

3 结论

利用数值计算对外加强制扰动引起的竖壁上蒸汽冷凝液膜波动强化传热过程进行了研究，得到以下结论:

(1)建立了等温竖直壁面上二维层流冷凝波动降液膜流动数值模型，对比NOSOKO波速与峰高的实验关联式验证了模型的准确性。在14 Hz的外加强制扰动作用下，液膜无法形成振幅连续递增的波动，波长分布较为分散。扰动＞16 Hz时，扰动频率的增加使波动间的相互作用趋势明显，波长和波频随液膜Re数呈现轻微的波动，16 Hz扰动频率下的波长和波速高于其他频率。

(2)界面面积增加不是波动强化传热的主要因素。扰动频率为16 Hz时的波动强化传热效果最为显著，传热系数增加了30%，对流作用是引起波动液膜的传热强化的主要因素，其贡献率为79%。