排水深隧衬砌管片混凝土力学特性研究

张慎河魏宏邢鲁义刘玉香杨景

(1.山东建筑大学 土木工程学院，山东 济南 250101；2.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590)

0 引言

近年来异常气候频现，城市化进程加快与城市排水系统发展缓慢的矛盾导致城市洪涝频发。我国平均每年有百余座城市因降水而内涝，人民生命财产受到极大损失，城市排水问题亟待解决。深隧排水系统可作为浅层排水系统的补充，进而提高城市防洪排涝能力[1-3]。深隧排水系统主要由竖井、主隧道、排水泵站等部分组成，降水带来的城市径流通过竖井流入主隧，再由系统末端的排水泵站排出。

目前大陆运营中的和在建的城市深隧排水系统，其主隧道埋深在地表40 m以下，施工建设多采用盾构法。隧道衬砌管片除长期承受围岩压力外，还因隧道“注满—溢流—置空”的状态承受周期性动态水压力作用。在静、动荷载的长期作用下，衬砌混凝土的性能会发生劣化，进而影响隧道结构的适用性和耐久性。为此，学者们对混凝土材料做了大量相关研究。ZHAO等[4]得出混凝土在循环加卸载作用下，会产生更多的微裂纹或损伤，从而导致更早的裂纹萌生和更低的临界力以及更小的断裂能。苏谦等[5]、肖诗云等[6]、石星等[7]和梁春华等[8]通过混凝土循环加卸载试验，得出混凝土不同物理参数变化规律。张慎河等[9-10]通过室内试验探究了类岩石材料的蠕变特性，得出了类岩石材料的长期强度确定方法。姜德义等[11]开展了混凝土的常规疲劳试验和不连续疲劳试验。FENG等[12]对自密实混凝土进行了不同幅值下加载试验，建立了不同幅值载荷下混凝土的损伤演化方程。肖杰等[13]通过开展不同侧压下的混凝土循环加卸载试验，建立了滞回环面积与循环次数之间的关系。多数学者在研究混凝土循环加卸载作用下的力学性能时，仅单纯加载至某一应力值后直接卸载并未考虑蠕变作用。深隧排水系统运行周期内，在隧道的“注满—溢流—置空”过程中存在荷载稳定期和荷载扰动期，其间引发的蠕变与扰动对衬砌混凝土性能将产生重要影响，亟须开展进一步研究。基于上述过程，对衬砌混凝土分别进行蠕变条件下的循环加卸载试验和扰动试验，研究城市排水深隧系统衬砌混凝土的力学性能，探索蠕变条件下循环加卸载作用和扰动作用所引起的衬砌混凝土的损伤演化规律和变形特征，从而为城市排水深隧系统的稳定运行提供科学依据。

1 试验设备与试件制备

1.1 试验设备

YUMT-1000岩石力学万能试验机最大可提供600 kN轴向力，能完成岩石类材料的常规压缩、劈裂、直剪等多项力学试验。TAW-1000D岩石流变扰动试验仪由动力驱动系统、轴压系统、围压系统、扰动系统、采集系统组成，能提供1000 kN最大轴向力、70 MPa最大围压和20 kN最大扰动荷载。

1.2 试件制备

试件为济南某管片制造有限公司制作的尺寸为100 mm×100 mm×100 mm的立方体标准试件，设计强度等级为C50。水泥为42.5级普通硅酸盐水泥；细骨料中砂细度模数为2.9，含泥量为0.6%；粗骨料碎石级配为5～25 mm连续级配，含泥量为0.6%；粉煤灰为F类，采用聚羧酸高性能外加剂。对标准试件进行钻孔取芯，制备Φ50×100 mm规格的圆柱体试件，如图1所示。

图1 圆柱体试件图

2 混凝土循环加卸载蠕变试验

在雨季，城市径流汇入竖井多次充满深部排水隧道使隧道衬砌承受水压力和围岩压力；而在非雨季，隧道处于备用状态即空置，隧道衬砌主要承受围岩压力。一年中包括雨季和非雨季两个时间段，隧道在“注满—溢流—置空”的过程中衬砌管片在围岩压力与水压力作用下经历一次加压和卸压过程。该种工况下，在隧道的设计使用寿命中，其衬砌管片将经历多个周期性的加载和卸载过程，故对混凝土进行循环加卸载蠕变试验。

2.1 试验方案

利用YUMT-1000岩石力学万能试验机对试样进行循环加卸载蠕变试验。试验前，取3个试件进行单轴常规压缩试验，得到试样的抗压强度分别为63.1、54.6、62.3 MPa，对试验结果取平均值确定单轴抗压强度为60.0 MPa，为后续循环加卸载和蠕变扰动试验做准备。由于隧道埋深不同，取单轴抗压强度的50%、60%、70%、80%为加载上限应力值，对应的荷载值分别为30、36、42、48 MPa。设置预静载为3 MPa，以0.5 kN/s的加载速度加载至上限应力值后蠕变10 h模拟置空时的衬砌受力状态，再以0.5 kN/s的卸载速度卸载至3 MPa后蠕变2 h模拟注满时衬砌受力状态，一次循环共12 h，模拟完成1 a隧道衬砌混凝土的受力行为。循环加卸载n次后取下试件，利用声波仪测得试件纵波波速并记录。然后加载到下一级上限应力，重复以上试验步骤。通过改变循环加卸载次数n(5、10、15)模拟不同周期下隧道“注满—溢流—置空”过程。

2.2 试验结果与分析

选取典型试件进行分析，以循环10次为例，试验结果如图2所示。不同循环次数下的加卸载应力-应变曲线均出现内凹形曲线，滞回环有不断向前“迁移”的现象[5]，随着循环次数的增加滞回环由“疏”到“密”的迁移现象越明显。

图2 混凝土试件应力—应变曲线图(循环10次)

2.2.1 变形模量随上限应力变化规律

对于弹塑性材料，当所受应力小于材料的屈服应力时，将弹性模量定义为常数；当所受应力大于材料屈服应力时，将变形模量定义为一个随着应力的大小与范围变化的量[14]。变形模量计算公式由式(1)表示为

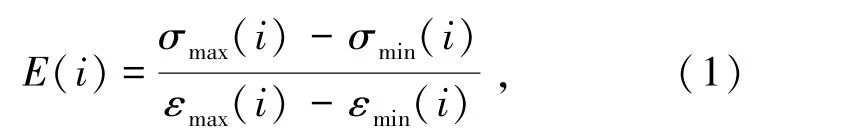
式中E(i)为每次加卸载割线模量，MPa；σmax(i)、σmin(i)分别为每次加卸载中的最大和最小应力，MPa；εmax(i)和εmin(i)分别为每次加卸载过程中的最大和最小应变。其中，每次加卸载过程中σmin(i)为预静载、εmin(i)为预静载对应的应变。

以循环10次的试件为例，分析数据得到混凝土加载、卸载变形模量和循环次数的变化曲线，如图3所示。相同上限应力下，混凝土加载变形模量随着循环次数的增加而增加。循环加卸载作用下，试样内部微裂纹将在每次循环加卸载过程中发生新的扩展，导致损伤逐渐累积[5]。前两次循环间的加载变形模量有一个突增值，第2次循环加卸载后相对于第1次循环加载变形模量分别增加29.95%、35.47%、19.31%和18.21%。混凝土在第一次受到荷载作用后其内部空隙被压缩，随着循环次数的增加混凝土内部逐渐密实，导致第2次循环后的加载变形模量增长趋势增加缓慢。上限应力分别加载至单轴抗压强度的50%、60%、70%时，混凝土的卸载变形模量随着循环次数的增加缓慢增加并趋于某一定值；荷载突破某一阈值加至80%时，卸载变形模量随着循环次数的增加先增加后减小；相同循环次数下，随着上限应力的增加，混凝土的加载卸载变形模量均呈现先增加后下降趋势，说明循环加卸载上限应力超出弹性范围。

图3 不同强度混凝土变形模量与循环次数关系图

2.2.2 残余塑性应变随上限应力变化规律

卸载后弹性变形恢复，塑性变形则以不可恢复的形式被保留。随着循环次数的增加塑性变形累加，对应的应变被称为累积塑性应变。总应变包括弹性应变和塑性应变两部分，由式(2)表示为

式中ε为总应变；εe为弹性应变；εp为塑性应变。将荷载作用下各循环次数所积累的塑性应变定义为累积塑性应变εc，由式(3)表示为

式中n＝1，2，3，…，15。

通过分析循环加卸载作用下混凝土轴向应变试验结果得到上限应力与累积塑性应变关系，如图4所示。相同循环次数下，随着上限应力的增加，混凝土累积塑性应变总体呈增长趋势，增长趋势伴随着循环次数的增加越来越明显。上限应力不变时，随着循环次数的增加，塑性变形不断积累，混凝土试件累积塑性应变亦呈增加趋势，说明混凝土在已进入弹塑性变形阶段，弹性变形随外力卸载能恢复，而塑性变形不能恢复并随着上限应力及循环次数增加不断累积。具体表现为上限应力为30 MPa时，循环10次比循环5次累积塑性应变值增加41%，循环15次比循环5次应变值增加了50%，增幅较小；上限应力为48 MPa时，循环10次的累积塑性应变值比循环5次的应变值增长了53%，而循环15次的应变值比5次的应变值增加87%，增幅显著提高。

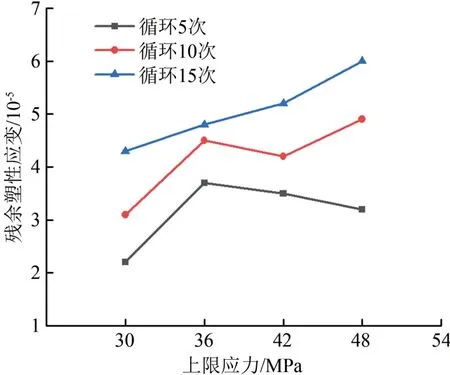
图4 上限应力与累积塑性应变关系图

2.3 混凝土试件损伤演化规律

定义损伤变量的方法主要有弹性模量法、超声波波速法、密度和重度法、能量法、应变法等[15]。其中声波波速法定义岩石材料的损伤得到广泛的应用[15-17]。在单轴加载过程中，试件微裂纹的闭合引起声波速度增加，而微裂纹的扩展则引起声波速度减少[18]，裂纹变化是引起声波波速改变的主要因素，故通过波速变化定义的损伤变量能反映岩石材料内部损伤的宏观现象。利用HS-YS4A型岩石声波参数测试仪对混凝土试件声波参数测试，声波波速测试结果见表1。

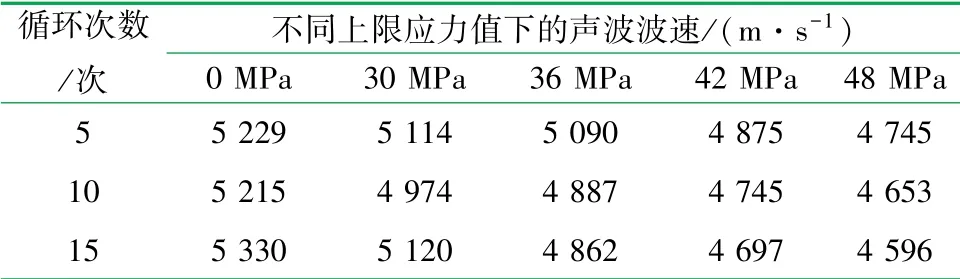
表1 不同循环次数和上限应力值下声波波速表

采用岩石声波波速定义损伤变量[18]公式计算并分析，损伤变量随应力变化情况如图5所示。上限应力自第二级至第三级过程中，混凝土内部粗骨料和砂浆交界面开始滑移，微裂缝进一步扩展，损伤变量增长较快。上限应力从第三级到第四级，混凝土内部原有的空隙、微裂隙被压密，导致损伤变量增长较为缓慢。随着循环次数增加，新的微裂隙出现，混凝土内部损伤进一步加剧。循环加卸载次数为10次时，损伤变量增长率较为平缓，斜率趋于常数。不同于其他两种情况，可能是圆柱体混凝土试件尺寸效应和内部的不均匀性所致。但总体来看，相同循环次数下，损伤变量与上限应力呈正相关关系，损伤变量增长率呈减小趋势。

图5 损伤变量与上限应力关系曲线图

3 混凝土蠕变扰动试验

雨季强降水所带来的城市径流小部分流入浅层排水系统，大部分从竖井灌入深隧排水系统。在落差较大情况下跌水使消能池水压迅速增加，水流汇入主隧道时冲击衬砌，使之承受冲击扰动作用。多次强降水会引起对隧道衬砌的多次冲击，每次冲击叠加起来相当于具有周期性的动水扰动作用。在此种工况下，长期冲击扰动荷载作用使衬砌结构的损伤加速，变形增加，最终导致衬砌开裂、洞顶混凝土的剥落甚至底部隆起变形等病害[19]。

3.1 混凝土蠕变扰动试验方案

载荷分级方法与循环加卸载试验相同，使用TAW-1000D岩石流变扰动试验仪试验。先加载至第一级荷载蠕变10 h，再对试件施加扰动。扰动频率设为1 Hz，扰动荷载波形为正弦波形，扰动幅值为0.5 MPa，扰动时间为60 s。待扰动蠕变变形稳定后施加第二次扰动，每次扰动间隔时间为15 min，共施加8次扰动，扰动总时长为2 h。用来模拟一个周期即一年内衬砌管片受到的扰动情况。第一级荷载施加完后施加下一级荷载，施加相同的扰动，直至四级荷载施加完毕。为探究不同扰动幅值的影响水平，再分别以1、1.5 MPa扰动幅值重复上述试验，以模拟不同埋深情况下隧道衬砌管片的扰动情况。

3.2 混凝土蠕变扰动试验结果分析

1 MPa扰动幅值下单轴蠕变扰动结果如图6、7所示。各级预静载蠕变10 h后，施加每一次扰动荷载后均出现一个突增应变，随着预静载的增加突增应变也逐渐增大。说明扰动荷载增加了混凝土的弹塑性变形，随着时间的增加弹性变形恢复，而塑性变形累积。在相同预静载下，累计扰动变形随着扰动次数的增加而增加，增速大致呈衰减趋势。最后一级预静载作用下，累计扰动变形曲线在前5次扰动施加后近似线性增加；从第6次扰动开始，混凝土试件在受到连续扰动作用后出现了硬化现象，扰动变形量增长较为缓慢。

图6 扰动幅值1 MPa蠕变扰动变形曲线图

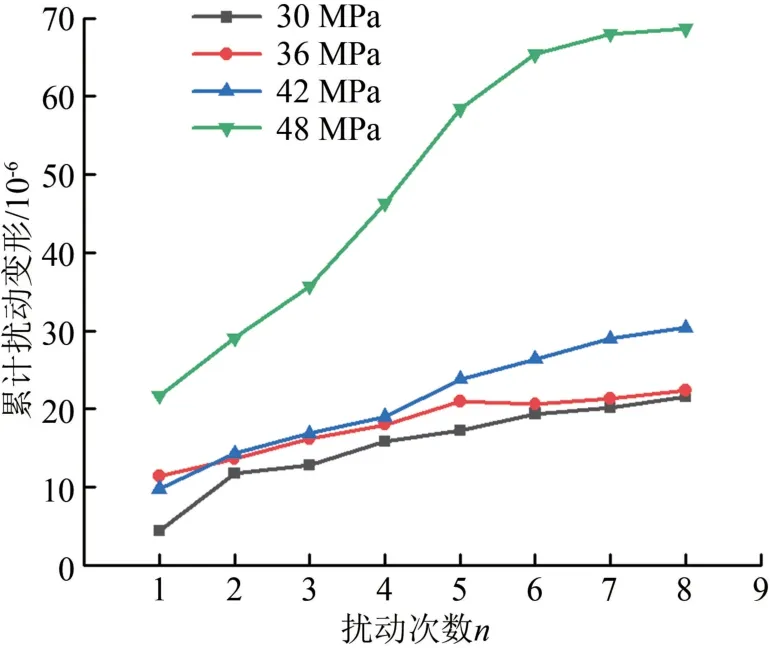
图7 扰动幅值1 MPa累计扰动变形曲线图

不同扰动幅值下应力与累计扰动变形之间关系曲线，如图8所示。扰动幅值为0.5 MPa时，随着应力增加累计扰动变形波动较大，变化规律不明显；扰动幅值为1 MPa时，累计扰动变形对应力变化较为敏感，随着应力的增加，累计扰动变形从21.6×10-6增加到68.7×10-6，增长了2.18倍近似指数型增长；扰动幅值较高为1.5 MPa时，随着应力的增加，累计扰动变形先减少后缓慢增加。前期的扰动作用使混凝土内部得微裂隙压密完好，再施加扰动荷载也难以产生较大变形，出现了变形硬化现象。

图8 不同扰动幅值下应力与累计扰动变形关系图

4 混凝土蠕变扰动力学模型与参数辨识

4.1 混凝土蠕变扰动力学模型的建立

岩石蠕变力学模型反映的是岩石材料在外界因素(荷载、温度等)作用下，应变-应力-时间之间的关系，运用数学方法对蠕变力学模型参数进行识别，从而揭示岩石的蠕变特性以及蠕变破坏的内在规律[20]。文献[21-23]指出伯格斯(Burgers)模型能较好地描述应力处于衰减蠕变阶段和稳态蠕变阶段蠕变特征。Burgers模型如图9所示。模型蠕变方程由式(4)表示为

图9 Burgers力学模型图

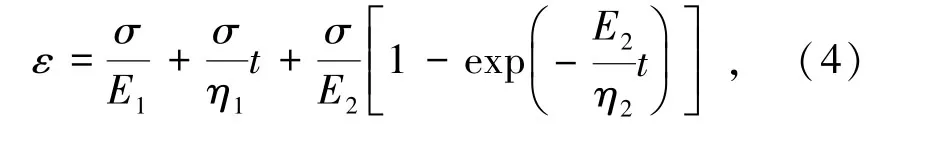
式中σ为加载应力，MPa；t为蠕变时间，min；E1为瞬时弹性模量，GPa；E2为黏弹性模量，GPa；η1、η2分别为黏滞系数，GPa·min。

扰动荷载作用下，混凝土蠕变曲线出现陡突，随着时间的增加，应变非线性变化越来越明显，引入文献[24]中非线性扰动蠕变元件，如图10所示。其中，σa用于判断元件是否起作用，为扰动应力阈值；η为塑性参数；tF为蠕变扰动启动时间。

图10 非线性扰动蠕变元件图

非线性扰动蠕变元件的变形方程由式(5)表示为

式中H(t-tF)为开关函数，具体由式(6)表示为

式中m为幂函数系数。

当加载应力超过扰动应力阈值，非线性扰动蠕变元件起作用，引入扰动损伤因子D，形成一个含有损伤因子的非线性扰动蠕变元件，如图11所示。

图11 含有损伤因子的非线性扰动蠕变元件图

将Burgers模型、含有损伤因子的非线性扰动蠕变元件进行串联，形成蠕变扰动力学模型，如图12所示。根据文献[25]将损伤因子D由式(7)表示为

图12 蠕变扰动力学模型图

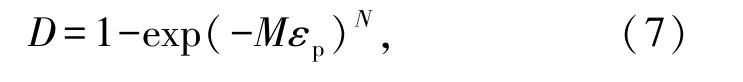
式中M、N分别为参数。

当σ≤σa且t≤tF时，蠕变扰动力学模型退化为Burgers模型，方程由式(8)表示为

当σ＞σa且t＞tF时，含有损伤因子的非线性扰动蠕变元件起作用，方程由式(9)表示为

式中η3为黏滞系数，GPa·min。

4.2 混凝土蠕变扰动力学模型参数辨识

进行非线性曲线拟合时迭代算法可选用列文伯格-马夸尔特(Levenberg-Marquardt)优化算法。该算法拟合参数时不需要考虑初始值选取问题，有效地解决了曲线难收敛问题。基于最小二乘法和Levenberg-Marquardt算法，对1 MPa扰动幅值下不同应力状态的蠕变扰动曲线进行辨识，得到的蠕变扰动力学模型参数见表2。

表2 蠕变扰动力学模型参数表

为了验证力学模型的正确性与可行性，需把拟合曲线与试验值进行对比分析，如图13所示，结果表明扰动后拟合曲线与试验曲线基本一致，验证了力学模型的合理性，表明所构造的力学模型可以合理地描述混凝土蠕变扰动后的蠕变变形特征。

图13 混凝土蠕变扰动力学模型拟合曲线与试验值的对比图

5 结论

对两种工况下的排水深隧衬砌管片混凝土分别进行循环加卸载蠕变试验和蠕变扰动试验，主要得出以下结论:

(1)上限应力不变时，衬砌混凝土试样的加载变形模量随循环次数的增加而增加；上限应力较低时，卸载变形模量随着循环次数的增加缓慢增加，而上限应力较高时，随着循环次数的增加卸载变形模量则先增加后减小。相同循环次数下，随着上限应力的增加，衬砌混凝土试样的加载、卸载变形模量先增加后减小；混凝土残余塑性应变、损伤变量随着上限应力和循环次数的增加而增大。

(2)施加扰动荷载后衬砌混凝土试件会产生突增应变；相同扰动幅值下，随着预静载的增加试件累计扰动变形总体上呈增大趋势，累计扰动变形随扰动次数的增加而增大；在较高扰动幅值下，累计扰动变形随扰动次数的增加先减小后缓慢增大，出现了硬化现象。相同循环次数下，损伤变量与上限应力呈正相关关系，损伤变量增长率呈减小趋势。基于Burgers模型，构造了含有损伤因子D的混凝土蠕变扰动力学模型，该模型能够合理地描述衬砌混凝土蠕变扰动后的变形特征。