GLC硅质轻型墙板轴心受压试验研究

焦红，马海程，王松岩，刘学光，姜晓雯

(山东建筑大学 土木工程学院，山东 济南 250101)

0 引言

随着我国装配式建筑的快速发展及建筑装配率的不断提高，三板(楼板、外墙板、内墙板)已成为装配式建筑中的重要组成部分。在GB/T 51129—2017《装配式建筑评价标准》[1]中，对非承重围护墙体采用非砌筑的比例提出了明确要求。我国建筑行业对预制墙板的需求量日益增加，各式各样的新型预制墙板应运而生，虽然其在力学性能方面能够满足围护结构的基本要求，但是也存在着结构形式复杂、制作工艺繁琐、综合造价较高等问题，难以满足市场需求。而采用湿法常温成型工艺的玻璃纤维网格布增强型硅质轻型墙板(GLC墙板)在制作过程中一次成型，且其生产工艺在建筑节能及经济性等方面有着明显优势，是一种符合国家装配式发展战略的新型预制墙板。

目前，学者们对预制墙板的轴心受压力学性能的研究主要集中在水泥基-钢丝网架夹芯板[2-4]、薄面板-冷弯薄壁型钢骨架组合墙板[5-8]和轻集料混凝土墙板[9-10]等其他材料及结构形式组成的墙板[11-13]。对于水泥基-钢丝网架夹芯墙板，芯材的弹性模量较小，在竖向轴心荷载作用下忽略其对承载能力及稳定性的贡献，而钢丝网架能够有效增强两侧水泥基面层的协同工作能力，对墙板的极限承载力和稳定性影响较大[14-15]。对于薄面板-冷弯薄壁型钢骨架组合墙板，其轴心受压性能主要取决于型钢骨架的截面形式[16]，而填充材料能显著提高该类墙板的抗压、刚度及延性等性能[17]；但在此类墙板的轴心受压计算公式中只考虑了冷弯薄壁型钢骨架的影响，忽略了面板与芯材对墙板整体稳定性的贡献[18]。赵考重等[19]基于混凝土结构轴心受压计算公式，提出了玻璃纤维混凝土灌芯石膏板的轴心受压计算公式，并以试验数据为依托，简化修正了稳定系数。杨曙兰等[20]研发了一种玻璃纤维夹芯泡桐木复合墙板，研究了轴向荷载作用下的承载力性能，通过欧拉公式计算复合墙板的临界荷载。GLC墙板的芯材与面层一体成型，作为其主要组成部分，二者对轴心受压性能的影响均不容忽视。目前，王松岩等[21-22]、焦红等[23]进行了GLC墙板的材料力学性能及抗弯性能等相关试验，得到了GLC墙板的本构关系及抗弯承载力公式。

综上所述，GLC墙板的材料复合形式不同于其他墙板，并且采用现行规范的公式无法准确预测其轴心受压承载力。因此，有必要深入研究GLC墙板的轴心受压性能及稳定性，通过分析高厚比对GLC墙板的承载能力、刚度及稳定性等性能的影响，提出适用于GLC墙板的高厚比限值及承载力计算公式，为该类墙板在工程中的设计和应用提供参考。

1 试验概况

1.1 GLC墙板及试验设计

GLC墙板由芯材(发泡水泥)、表皮专用水泥砂浆、耐碱玻璃纤维网格布经湿法成型工艺复合而成；芯材以硅质材料为基材，掺加增强剂、防水剂、发泡剂等外加剂经化学发泡制成。因反力架高度限制，为了保证试件高厚比的变量范围，试件厚度选择80 mm，四周砂浆面层厚度均为4 mm，墙板组成及截面具体尺寸如图1所示。

图1 GLC墙板组成及截面尺寸示意图

为研究GLC墙板在轴心竖向荷载作用下高厚比对GLC墙板受力性能的影响，试验设计了5组不同高度的试件，以此探究GLC墙板的高厚比限值及承载能力，各试件参数见表1。B为GLC墙板的宽度，高厚比β为试件计算高度H0与厚度h之比(试件为两端铰接，故计算高度H0取试件高度H)。

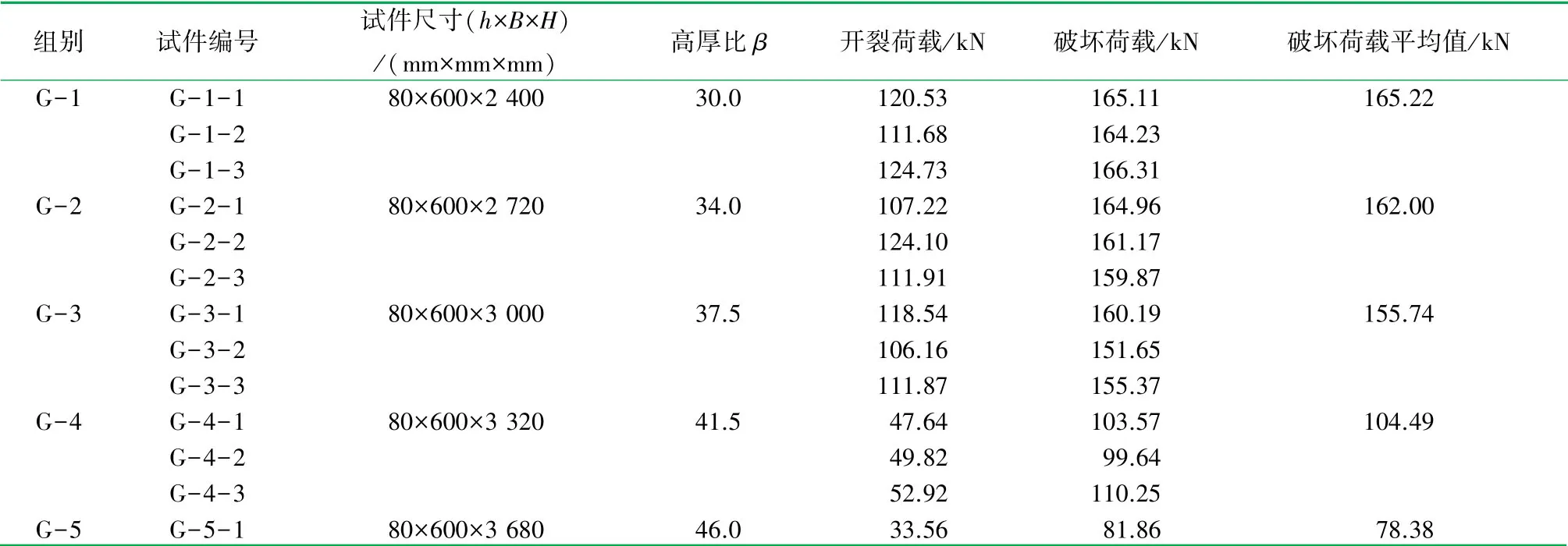
表1 轴心荷载试件的试验设计参数及试验结果表

1.2 GLC墙板基本力学性能

墙板抗压强度根据GB/T 23451—2009《建筑用轻质隔墙条板》[24]规定:沿墙板的板宽方向依次截取厚度为条板厚度尺寸、高度为100 mm、长度为100 mm的单元体试件进行抗压强度试验，如图2所示。

图2 GLC墙板试件破坏形态图

试件弹性模量根据JGJ/T 70—2009《建筑砂浆基本性能试验方法标准》[25]进行试验，试件尺寸为80 mm×80 mm×220 mm，试件尺寸及试验结果见表2和3。

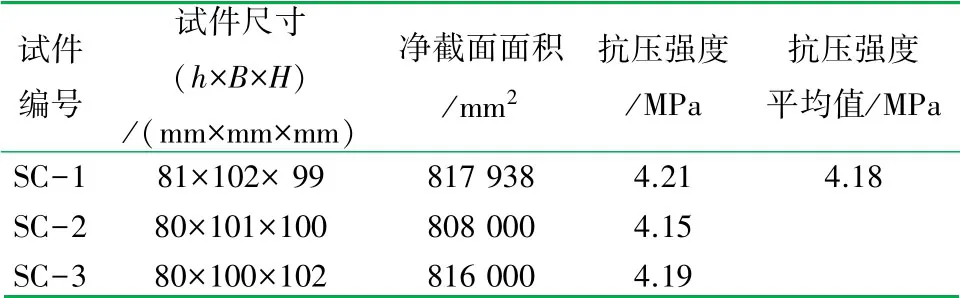
表2 GLC墙板基本力学性能试验结果表

表3 GLC墙板基本力学性能试验结果表

当试件破坏时，砂浆表皮与芯材未脱离，其协同工作效果较好，可看作一个整体。因此，取4 MPa作为GLC墙板的抗压强度标准值，取2800 MPa作为GLC墙板的整体弹性模量。

1.3 加载方案及测量方法

1.3.1 加载方案

试验采用自反力架进行加载，墙板顶端放置分配梁，将集中荷载转化为均布荷载作用于墙板上；为了模拟轴心受压状态，GLC墙板上、下两端放置单向铰支座，加载装置如图3所示。

试验时采用物理对中、分级加载的方法；预估荷载为试件在竖向荷载作用下轴心受压的理论破坏荷载，即墙板截面的整体抗压强度与截面面积的乘积。

(1)预加载，检测各仪器是否正常运行，加载阶段的荷载约为预估荷载的10%，且在2 min内加载完成，随即卸载，卸载时间与加载时间相同，反复加载、卸载3次后正式加载；

(2)正式加载的每级荷载约为预估荷载的10%，且在2 min内加载完成，每级加载持荷时间为10 min；在试件充分变形后进行数据采集，直至试件丧失承载能力，最后使用表格记录数据，加载曲线示意图如图4所示。

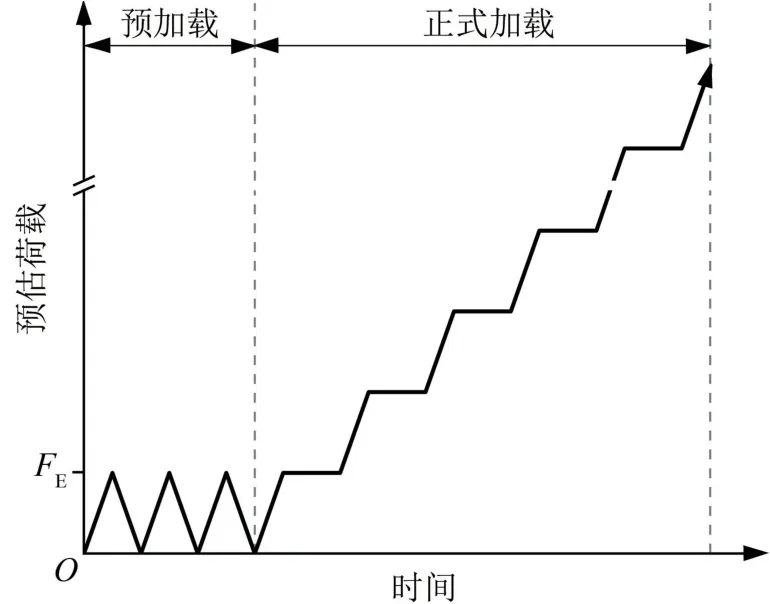
图4 加载曲线示意图

1.3.2 测点布置

为了考察轴心竖向荷载对试件不同截面纵向应力应变的影响，分别在试件正反两面跨中、1/8、3/8、5/8、7/8处布置纵向应变片A1～A5及B1～B5；为测试试件的平面外变形，分别在墙板跨中及上、下1/3处布置位移计；力学传感器采用轮辐式压力传感器，以上测量装置均连接TZT3826E数据采集系统进行数据采集，测点布置同样如图3所示。

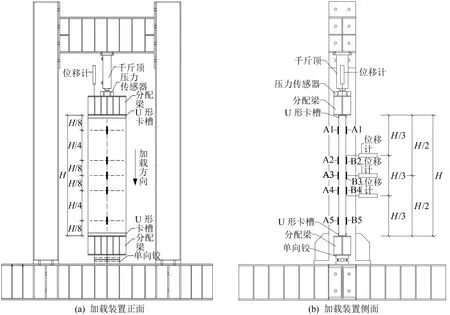
图3 加载装置与测点布置示意图

2 试验现象、结果及分析

2.1 试验现象

G-1与G-2组试验现象较为相似，试件加载至极限荷载的65%～77%时试件上端芯材产生竖向裂缝；加载至荷载的69%时，墙板中部表面出现横向裂缝；加载至极限荷载的80%时，试件发生轻微挠曲；而当加载至破坏荷载时，墙板发出巨响后折断，墙板受拉面破坏区域表面产生密集的横向细微裂缝，受拉侧芯材产生明显的受拉裂缝，玻璃纤维网格布未断裂，但已发生明显的受拉屈服，受压面芯材被压碎，如图5(a)和(b)所示。

G-3加载前期无明显现象，加载至极限荷载的70%～74%时，上端部产生竖向裂纹，加载至极限荷载的82%时发出沙沙声，最终破坏时的墙板发出巨响，墙板上端部两面鼓曲，芯材被全截面压碎，如图5(c)所示。

G-4与G-5试件的破坏特征较为相似，墙板在极限荷载的40%～50%就发生了开裂及明显的平面外失稳的趋势。随着荷载的增加，挠曲程度逐渐加大，最终墙板折断发生失稳破坏，如图5(d)和(e)所示。

图5 GLC墙板试件破坏现象图

2.2 试验结果分析

GLC墙板的轴心受压性能试验结果见表1。根据统计的数据可以得出:G-1组的各试件加载至极限荷载的65%～77%时试件上端芯材产生竖向裂缝；加载至69%时试件时墙板中部表面出现横向裂缝；G-2组的各试件加载至极限荷载的34%～40%时试件发出轻微响声，但墙板整体无弯曲现象；加载至66%～72%时，试件上端出现裂缝；G-3组的各试件加载前期无明显现象，加载至极限荷载的70%～74%时上端部产生竖向裂纹，G-4与G-5组的各试件破坏特征较为相似，在极限荷载的40%～50%就发生了开裂。

对比5组墙板试件的整体破坏状态可知:

(1)G-1和G-2组墙板试件的破坏形态为先产生竖向裂缝随即折断，加载前期无明显的挠曲现象，最终虽都有轻微的失稳趋势，但其破坏形态主要归咎为截面不均匀材性破坏导致的偶然性折断；

(2)G-3组墙板为墙板顶部受压劈裂破坏，其主要破坏机理与G-1、G-2较为一致，最终都是由于板顶因受压劈裂破坏到导致承载能力和稳定性丧失；

(3)G-4和G-5组墙板试件在加载初期出现了明显的挠曲，其都是由于高厚比过大，弯曲刚度较低，在挠曲二阶效应的影响下，将偶然因素的影响不断放大，最终发生了平面外失稳破坏。

G-1、G-2组与G-4、G-5组墙板试件的破坏形态较为相似，但其不同的是:由于墙板芯材发泡的不均匀性，G-1和G-2在轴向压缩阶段的墙板材料破坏程度不平衡，使得试件在加载后期产生挠曲现象并随即破坏；而G-4和G-5试件端部无竖向裂缝开展，只存在折断处的受弯破坏特征，并且开裂荷载与极限荷载的比值远小于前者，过早地进入失稳阶段，伴随挠曲二阶效应最终发生失稳破坏。

高厚比较小的试件受压后先在端部出现裂缝，随着荷载的增加，试件破坏形态发展为折断破坏或局部受压破坏，破坏时跨中挠度较小，其挠度位于5～10 mm之间；高厚比较大的试件在加载至极限荷载的40%～50%时，试件过早地开裂及发生明显的挠曲现象，并随着挠曲二阶效应，挠曲程度不断增加，最终发展为平面外失稳破坏，破坏时跨中挠度较大，其挠度均位于34～44 mm之间。

2.2.1 荷载-侧向挠度曲线

选取每组的典型试件，将试件的侧向挠度与轴向荷载变化关系曲线绘制如图6所示。由荷载-侧向挠度曲线表明:G-1、G-2、G-3组墙板试件在加载初期，随着荷载的增加，各试件侧向挠度均呈线性增长，处于弹性阶段，且初始刚度基本相同；随着荷载的增加，高厚比较大的墙板试件极限承载力有所减小，但减小幅度不明显。G-4、G-5组墙板试件在加载初期无明显的弹性阶段，随着荷载的增加，墙板试件侧向挠度增长较快，并较早地进入塑性阶段。

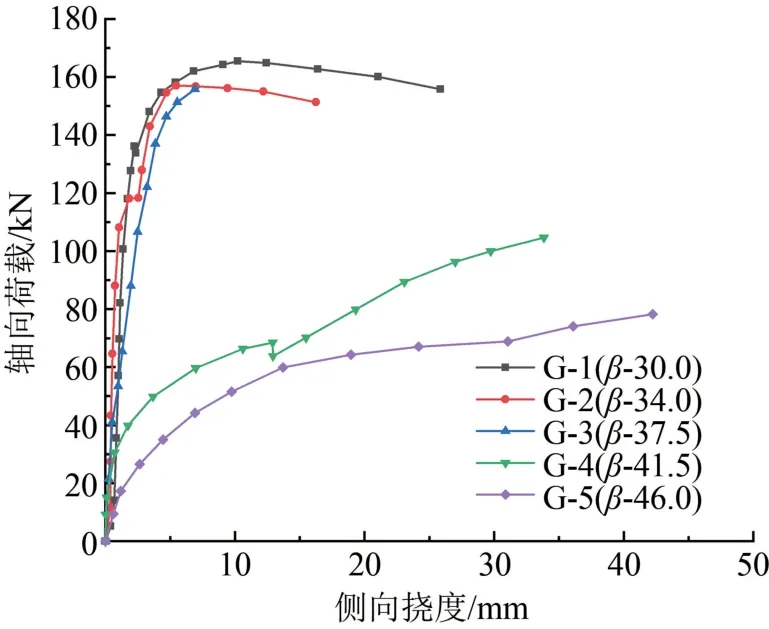
图6 荷载-侧向挠度曲线图

对比5组试件的荷载-侧向挠度曲线可知，与高厚比较小的墙板试件相比，随着荷载的增加高厚比较大的墙板试件刚度减小较为显著。当β≤37.5时，随荷载的增大，试件跨中的侧向挠度基本上保持线性增长，侧向挠度增长速率缓慢，在荷载达到极限荷载的72%～80%时侧向挠度才有所增加；当β＞37.5时，整段曲线已无明显弹性阶段，在挠曲二阶效应的作用下，试件跨中的侧向挠度增长速率随荷载逐渐加快，过早地进入失稳阶段，侧向挠度增长幅度较大。可见，试件高厚比越大挠曲二阶效应越显著，试件也越容易发生失稳破坏；G-4、G-5相对于G-1、G-2、G-3组墙板试件，失稳破坏现象更加显著，塑性变形阶段的偏移量较大，表明试验中β≤37.5的试件稳定性较好。

2.2.2 荷载-纵向应变曲线

丽晶公司采用了美国联邦最高法院(以下简称最高法院)一百多年前的迈尔斯案中不予支持的转售价格维持的定价方式。尽管从地区法院到巡回法院均已败诉，但为了捍卫自己的商业模式，丽晶公司上诉到了最高法院。在丽晶公司的定价策略中处于核心地位的是转售价格维持。它意味着在经销商层面取消价格折扣。从表面上看，取消折扣是反竞争的，毕竟折扣有利于消费者。丽晶公司必须说服法庭减少折扣能够增进消费者福利，它最终获得了成功，最高法院以5:4的微弱比例判决丽晶公司胜诉。

取1/2处纵向应变片A3和B3的应变值，试件的轴向荷载与其应变值的变化关系曲线如图7所示，G-1、G-2和G-3组墙板试件在加载前期，两面的纵向压应变随着荷载的增加，增长趋势较为统一，此时墙板试件刚度也较为稳定；在加载后期两面的压应变增长趋势发生偏离，一面的压应变持续增长，另一面的压应变增长缓慢或逐渐减小；而G-4、G-5在加载前期就发生了明显的偏离，且G-5墙板试件一侧的压应变转为拉应变，两组墙板试件刚度下降较明显。

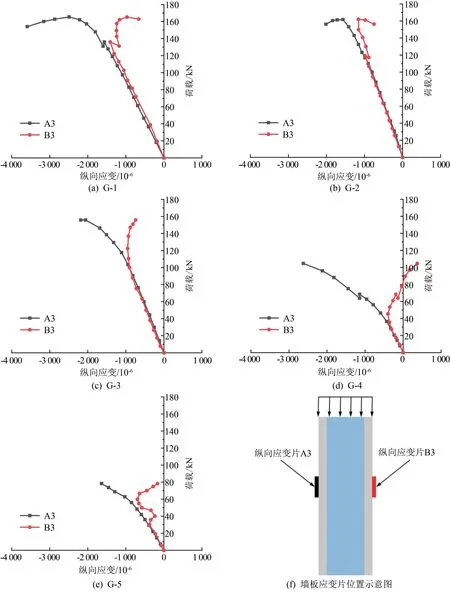
图7 荷载-纵向应变曲线图

分析各墙板试件两面应变的偏离点，各墙板试件偏离点处的荷载与极限荷载的比值随着高厚比的增加呈减小趋势。G-1、G-2和G-3墙板试件两面的应变在极限荷载的71%～83%时出现偏离，墙板试件在两面的应变在极限荷载的29%至45%时出现偏离。由此可见，高厚比β≤37.5相比于高厚比β＞37.5时，墙板试件两面的应变偏离较晚。

G-1、G-2与G-4、G-5的破坏同样具有明显区别。G-1、G-2是由于材料的不均匀性等缺陷造成在截面高度方向的压应力失衡，与G-1、G-2不同的是，G-4、G-5是由于试件高厚比较大，初始弯曲刚度小，产生的初弯曲较大，试件在加载前期就在初弯曲的作用下伴随挠曲二阶效应发生较早的失稳现象。

2.2.3 GLC墙板受压承载力分析

根据上述分析表明GLC墙板的高厚比对极限承载力影响较大，故应研究其极限承载力与高厚比的关系，GLC墙板随高厚比变化的极限承载力关系曲线如图8所示。

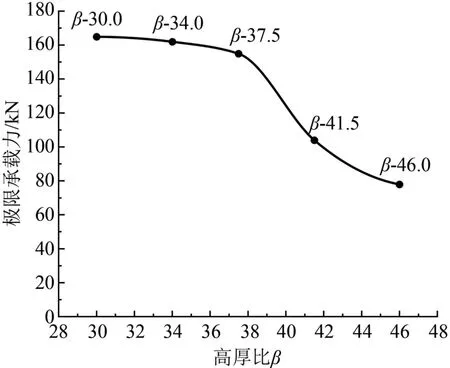
图8 GLC墙板极限承载力-高厚比关系曲线图

相比于G-1组墙板试件，G-2、G-3、G-4和G-5组墙板试件的极限承载力分别降低了2%、6%、37%、53%；G-4、G-5组相比于G-2、G-3组墙板试件极限承载力下降趋势较为显著。

如图8所示，GLC墙板的承载力随高厚比的增加呈非线性减小，且在高厚比β＞37.5后有显著下降的趋势。上述变化规律的主要原因在于高厚比较大(β＞37.5)的墙板试件，其几何缺陷(初始弯曲、墙板的初始不平整度)与力学缺陷(弹性模量、截面强度极限的不均匀性)在挠曲二阶效应的作用下被逐渐放大，从而墙板试件的弯曲刚度逐渐减小，墙板试件更易发生失稳。

上述试验分析表明，极限承载力-高厚比关系曲线与试件的破坏形态、荷载-侧向位移曲线、荷载-纵向应变曲线的分析结果较为一致，GLC墙板在高厚比β≤37.5时的稳定性更加可靠。但由于试验条件与生产工艺的限制，试件存在的各种初始缺陷对试验结果产生了一定的影响，因此应对GLC墙板的高厚比限值与轴心受压承载力进行理论分析与计算，并对比与验证了试验结果。

3 GLC墙板轴心受压稳定性分析与承载力计算

3.1 GLC墙板高厚比限值理论计算

根据赵成文等[26]建议的高厚比限值理论计算方法，以压杆稳定理论为基础计算GLC墙板的理论高厚比限值。

(1)构件是理想的等截面直杆；

(2)压力始终作用在初始轴线上；

(3)GLC墙板表皮砂浆与芯材协同工作状态较好，故抗压强度平均值与弹性模量采用墙板试块的试验结果；

(4)材料在失稳前符合胡克定律，即应力应变成线性关系。其中，GLC墙板试块的比例极限为0.45fm。

文献[22]中对欧拉公式的推导由式(1)表示为

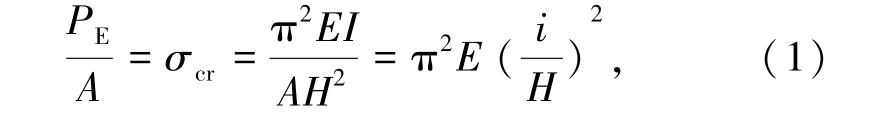
式中PE为临界荷载，kN；A为截面面积，mm2；σcr为临界应力，MPa；E为GLC墙板的弹性模量；I为截面惯性矩，cm4；i为回转半径，i＝0.289h，mm。

根据式(1)的推导，高厚比β可由式(2)表示为

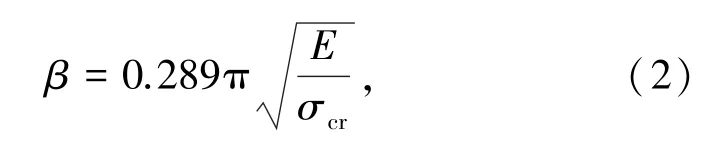
式中σcr＝0.45fm。

由上述材性试验可知抗压强度标准值fm为4 MPa，整体弹性模量E为2800 MPa，将其代入式(2)计算得GLC墙板轴心受压理论高厚比限值为35.79。

3.2 GLC墙板高厚比限值研究

与β≤37.5的试件相比β＞37.5的试件更易出现失稳破坏现象，且其极限承载力较为稳定。因此，β≤37.5的试件的整体稳定性较为可靠。

理论计算的β限值为35.79，虽然其小于试验值，但数值较为接近，可认为理论计算较为合理但偏于保守，具有一定的安全储备。

结合理论计算与试验验证，当β较大时，不但GLC墙板承载力较低，而且稳定性也较差，存在一定安全隐患。因此，建议GLC墙板轴心受压构件的β限值为35，此建议值为GLC墙板在轴心受压状态下的β限值，而GLC墙板上端与结构采用柔性连接，故建议值偏安全。

3.3 GLC墙板承载力计算公式

随着高厚比的增加，试件将会产生纵向弯曲，因此GLC墙板的承载力受稳定系数的影响，试件承载力将会随着高厚比的增加而降低；GLC墙板的承载力计算公式可由式(3)表示为

式中Nu为GLC墙板极限承载力，kN；φ0为轴心受压GLC墙板稳定系数；fgc为GLC墙板的抗压强度标准值，取4 MPa。

由式(3)可知，稳定系数φ0可由式(4)表示为

各组试件的稳定系数φ0的计算结果见表4。

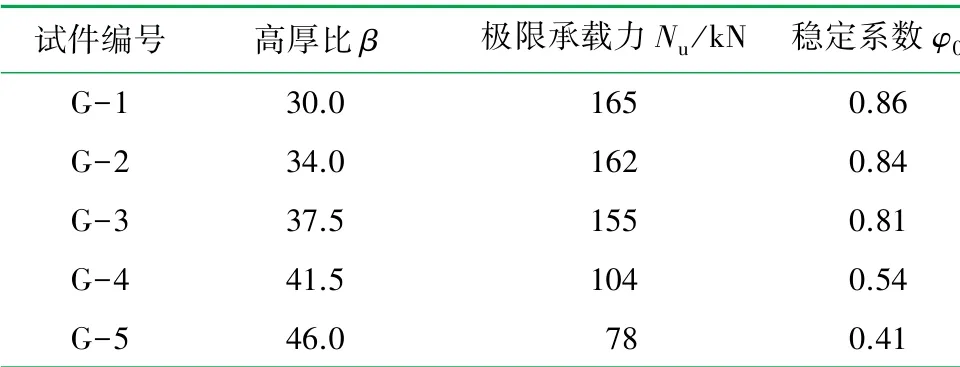
表4 各组试件稳定系数表

如图9所示，稳定系数随着β的增加出现了明显 的 下 降 段，且 下 降 趋 势 较 为 显 著，因 此GB 50003—2011《砌体结构设计规范》[27]中稳定系数计算公式中的参数值不再适用GLC墙板，但其β与影响系数的表示形式在β≤37.5的区段仍然适用；故在β≤37.5的区段采用GB 50003—2011[23]中β和稳定系数关系的表示形式，在β＞37.5的区段采用指数模型。

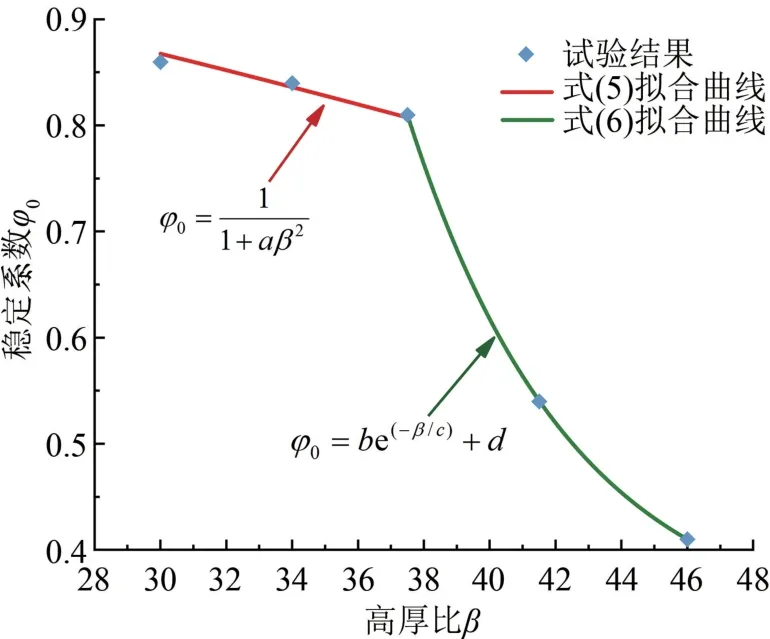
图9 稳定系数-高厚比关系曲线图

GLC墙板的稳定系数φ0可由式(5)和(6)表示为

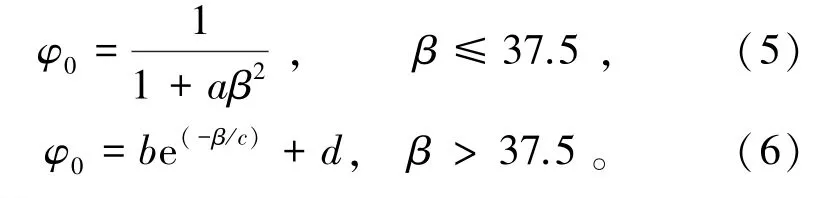
采用数值模拟软件对稳定系数φ0与高厚比β关系进行非线性拟合，拟合曲线如图9所示，可得出各参数的标准误差较小，式(5)的相关系数为0.94，而式(6)的相关系数为0.99，拟合程度较好，见表5。

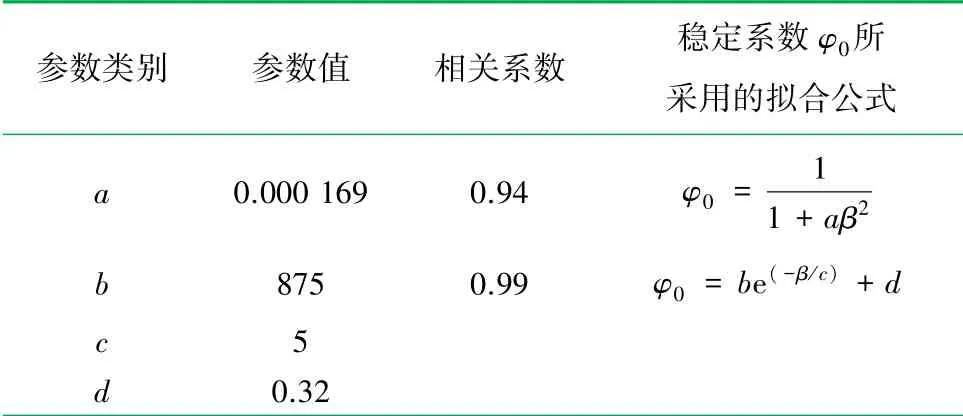
表5 拟合参数表

虽然式(5)和(6)拟合程度较好，代入式(3)后计算结果与试验结果较为吻合，但在实际工程应用中应赋予其一定的安全储备，因此在承载力计算时将a调整为0.000169，d调整为0.30。将上述调整后的各参数代入式(5)和(6)得到的稳定系数φ0可由式(8)和(9)表示为

式(8)和(9)代入式(3)所得到的计算结果与试验结果见表6。β≤37.5时的误差均＜3%，且误差平均值为1.90%；β＞37.5时，误差均＜5%，且误差平均值为4.01%；试验结果与计算值误差较小，均在可接受范围内，式(3)计算的GLC墙板轴心竖向承载力与试验结果吻合程度较好且偏于保守，有一定的安全储备。其中，误差由式(10)表示为

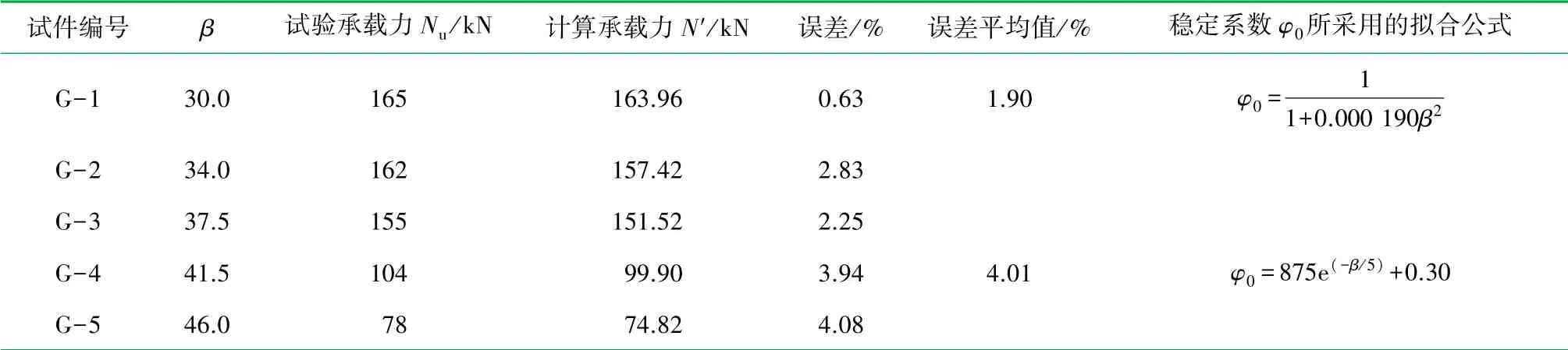
表6 GLC墙板试件试验结果及计算结果表

4 结论

分析5组GLC墙板的轴心受压试验研究结果，得到以下结论:

(1)随着高厚比的增加，GLC墙板承载力呈非线性减小，并具有显著下降的趋势；相比于β≤37.5的墙板，β＞37.5的墙板的承载力与稳定性下降较多，更易发生失稳破坏，因此β≤37.5的GLC墙板更加可靠。

(2)理论计算得到的高厚比限值35是偏于安全的，建议GLC墙板的高厚比不宜＞35。此建议值为GLC墙板在轴心受压状态下的高厚比限值，由于GLC墙板上端与结构是采用柔性连接，因此有一定的安全储备。

(3)提出了GLC墙板的承载力与稳定系数计算公式，计算值与试验值吻合较好，可为GLC硅质轻型墙板的应用技术规程提供一定的试验依据，同时可为进一步研究GLC墙板的工程应用提供参考。