基于Voronoi图的金洞林场闽楠人工林林木种内、种间竞争的研究

孙亚萍，曹小玉，李际平，赵文菲，谢政锠，莫永俊，袁 达

(中南林业科技大学林学院，湖南 长沙 410004)

竞争普遍存在于森林生态系统中，是森林空间结构状态的重要组成部分[1]。在同一片生境中，林木之间为了获取更多的阳光、土壤资源和水资源等，导致部分林木所需环境资源不足，从而影响个体生长发育[2-4]。因此，开展林木竞争关系的相关研究，有助于揭示林木的竞争机制，对后期森林的可持续经营具有重要指导意义[5-7]。

目前，国内外众多学者提出了不同的竞争指数模型来描述林木之间的竞争强度[8]，其中Hegyi竞争指数模型[9]被广泛地应用于森林经理中[10-11]。段仁燕等[12]、吴振新等[13]和付梦瑶等[14]基于胸径与林木空间分布的组合形式来研究林木种内种间竞争。汤孟平等[15]考虑到Hegyi竞争指数不能统一确定竞争单元尺度的缺陷，提出了基于Voronoi图的加权竞争指数，在此基础上，提出了V_hegyi竞争指数。Weiner[16]提出了邻体干扰竞争指数模型，表明竞争木的影响程度与其个体大小相关。但这些研究忽略了较高的植物在光竞争中更有竞争优势[17-20]。有研究表明，在林木完整的生长周期中光资源垂直供应，光竞争与植物个体大小有关，较高的林木优先获得光资源，其捕获的光能用于扩大更多的受光面积，因此，林木在竞争状态下，较高的林木遮阴效果会越来越强，树高因素会导致林木间资源分配不均衡。林木凭借株高优势遮挡周围的矮小植株，阻碍小个体林木获得充足的光照，而植被冠层下的小个体对高个体光竞争影响不大。基于此，本研究以金洞林场闽楠(Phoebebournei)人工林为研究对象，采用Voronoi图确定林木的空间结构单元，考虑了在同时争夺光照资源时，较高的林木比较矮林木更有竞争优势的前提下，利用Pearson相关分析法和曲线拟合比较分析Hegyi简单竞争指数、综合竞争指数(含胸径、树高、冠幅及林木间距离因子)、剔除该模型中比对象木矮的竞争木后的Hegyi简单竞争指数和综合竞争指数，比较分析4种竞争指数的优劣，筛选出更适于描述闽楠人工林竞争机制的竞争指数，为后期对森林的结构调整及经营管理提供依据。

1 研究区域概况

金洞林场位于永州市祁阳县南，地理位置110°53′43″E，26°02′10″N。位于南岭山系的阳明山脉东北部，东北低、西南高，境内山峦起伏，年平均气温为16.5～17.7 ℃，年降水量在1 600～1 890 mm之间，土壤包括红壤、黄红壤、山地黄壤以及山地黄棕壤。林场所辖国土区域为53 963 hm2，森林覆盖率达到了87.74%。林场内植被繁茂，乔木树种主要有闽楠、南方红豆杉(Taxuswallichiana)、香樟(Cinnamomumcamphora)、阿丁枫(Altingiachinensis)、杉木(Cunninghamialanceolata)、杜仲(Eucommiaulmoides)和木荷(Schimasuperba)等。

2 材料与方法

2.1 研究对象

在金洞林场选择立地条件一致的林分，设置3块20 m×30 m的固定样地，对标准地内每株胸径≥5 cm、树高≥1.3 m以上的树木进行每木检尺，逐株记录相对坐标(x，y)，测定内容包括胸径、树高、第一活枝高和东西南北冠幅等主要测树因子。

表1 各样地基本情况Tab.1 Basicinformationofsampleplots样地号密度/(株·hm-2)树种组成平均胸径/cm平均树高/m平均冠幅/(m×m)19835闽4木1阿11.510.72.3×2.4215005闽5木-樟15.614.22.7×2.7315165闽5杉12.911.62.5×2.5 注:闽为闽楠;木为木荷;阿为阿丁枫;樟为香樟;杉为杉木。

2.2 研究方法

2.2.1 竞争单元的确定

采用Voronoi图来确定林木竞争单元，使对象木与竞争木具有最大关联性，同时也提高了对林木竞争的研究精度。利用ArcGIS 10.4中的泰森多边形生成Voronoi图。每一个泰森多边形为Voronoi图的最小组成单元，每一个Voronoi图内只包含1株林木即对象木，邻近木株数等于其边数，其邻接Voronoi图所包含的林木即为该林木的邻近木(见图1)。

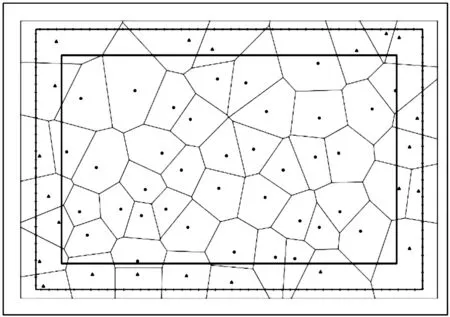
图1 基于 Voronoi 图的竞争单元Fig.1 Competitive unit based on Voronoi diagram

2.2.2 边缘校正

为减少样地边缘林木受到边界外林木的影响，对样地进行边缘矫正。本研究去除边缘效应的方法是：把位于样地边缘的林木直接记录成竞争木，在样地四周设置2 m宽的带状缓冲区；在缓冲区以外的林木为边缘木，只作为中心木的邻近木存在，而位于缓冲区内的林木均作为参照木参与计算。

2.2.3 竞争指数的确定

(1)Hegyi简单竞争指数

采用竞争木与中心木的胸径比值与二者之间距离之比来衡量林木间的竞争关系，用公式表示为：

(1)

式中：H为对象木i的竞争指数；Di为对象木i的胸径；Dj为竞争木j的胸径；Lij为对象木i与竞争木j之间的距离。

(2) 综合竞争指数

综合竞争指数是基于Hegyi简单竞争指数基础之上，以林木胸径、树高、冠幅乘积与对象木的胸径、树高、冠幅乘积的比值再乘以两者之间距离的倒数。用公式表示为：

(2)

式中：C为对象木的综合竞争指标；Di为对象木i的胸径；Dj为竞争木j的胸径；Hi为对象木i的树高；Hj为竞争木j的树高；CWi为对象木i的冠幅直径；CWj为竞争木j的冠幅直径；Lij为对象木i与之相对应的竞争木j之间的距离。

(3)修订后的Hegyi简单竞争指数和综合竞争指数

本文还选择了更改后的2个公式作为参考，剔除该模型中比对象木矮的竞争木后的Hegyi简单竞争指数和综合竞争指数，修改后的公式(用下标“m”表示)只考虑对象木同层或上层的竞争木(STj≥STi，其中STj是竞争木的冠层高度，STi是对象木的冠层高度)。用公式表示为：

(3)

(4)

这种修改是基于Hegyi简单竞争指数和综合竞争指数，试图用树高作为筛选林木竞争的指标，只选对象木的旁边较高的树为竞争木。其主要原因是Hegyi竞争指数通常量化双边竞争[21]，较高的树优先获得光资源的能力强，这种限制可能会导致对象木较低的树无法与比对象木高的竞争木竞争光照[22]。

2.3 数据分析

通过Microsoft Excel 2013软件进行数据处理，利用SPSS 25.0统计软件完成林木胸径与不同方式确定的竞争指数的Pearson相关性分析。

3 结果与分析

3.1 对象木和竞争木的基本情况

由表2可以看出：在整个研究区内闽楠、杉木和木荷占有重要地位，闽楠在三块样地中占对象木株数比例均达到或超过50%，其他树种主要是杉木、阿丁枫和香樟,为零星分布的伴生树种。1号样地内对象木和竞争木中，闽楠占比最大，但其平均胸径均小于木荷；阿丁枫对象木株数最少，仅占1号样地总株数的13.6%。2号样地内对象木共有3种，分别为闽楠、木荷和香樟，闽楠和木荷株数占该样地的总株数的98.9%，二者平均胸径接近，分别为15.6 cm和15.5cm；香樟仅有一株，对该样地的闽楠和木荷的竞争态势影响不大。3号样地中对象木仅有2种，闽楠和杉木的株数占比较为平均，这说明金洞林场闽楠人工林中，闽楠与其他树种混交度良好，该样地中所有对象木的平均胸径在11.0～19.0 cm之间，竞争木的平均胸径大部分集中在12.0～18.0 cm之间。

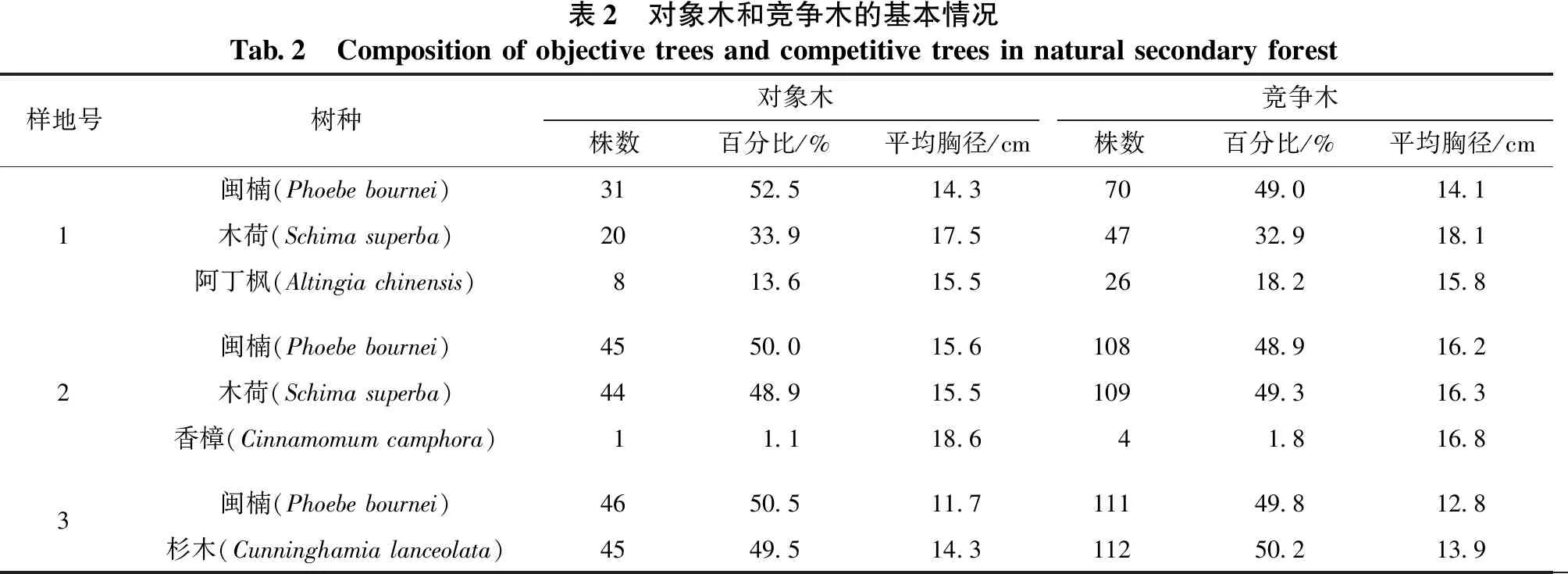
表2 对象木和竞争木的基本情况Tab.2 Compositionofobjectivetreesandcompetitivetreesinnaturalsecondaryforest样地号树种对象木竞争木株数百分比/%平均胸径/cm株数百分比/%平均胸径/cm闽楠(Phoebebournei)3152.514.37049.014.11木荷(Schimasuperba)2033.917.54732.918.1阿丁枫(Altingiachinensis)813.615.52618.215.8闽楠(Phoebebournei)4550.015.610848.916.22木荷(Schimasuperba)4448.915.510949.316.3香樟(Cinnamomumcamphora)11.118.641.816.83闽楠(Phoebebournei)4650.511.711149.812.8杉木(Cunninghamialanceolata)4549.514.311250.213.9

3.2 竞争指数与胸径的相关分析

3.2.1 不同竞争指数与对象木胸径相关分析

由表3可以看出：3块样地的林木胸径与4种竞争指数的Pearson相关系数均为负值，表明不同的竞争指数与林木胸径呈负相关关系，且均在0.01水平上呈现极显著相关(P<0.01)，Pearson相关系数的绝对值表现出综合竞争指数高于简单竞争指数，即C>H、Cm>Hm，且剔除比对象木矮的竞争木后的简单竞争指数和综合竞争指数均高于剔除前，即Hm>H、Cm>C。

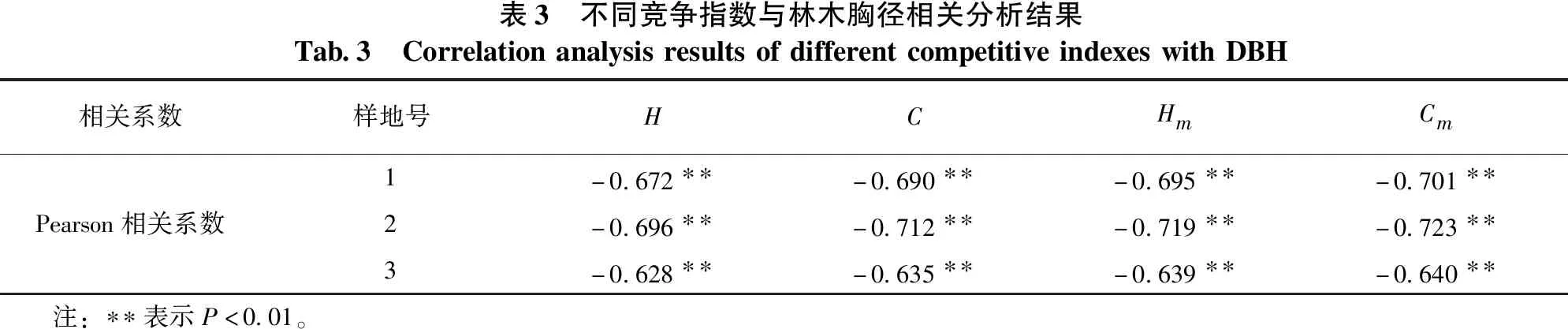
表3 不同竞争指数与林木胸径相关分析结果Tab.3 CorrelationanalysisresultsofdifferentcompetitiveindexeswithDBH相关系数样地号HCHmCm1-0.672∗∗-0.690∗∗-0.695∗∗-0.701∗∗Pearson相关系数2-0.696∗∗-0.712∗∗-0.719∗∗-0.723∗∗3-0.628∗∗-0.635∗∗-0.639∗∗-0.640∗∗ 注:∗∗表示P<0.01。

3.2.2 不同竞争指数与对象木胸径的拟合曲线

为了研究金洞林场闽楠人工林的种内种间竞争强度关系，以对象木胸径为自变量、以竞争指数为因变量进行回归拟合，在对比不同的回归方程模型后，选择幂函数来拟合竞争指数与胸径的关系。从图2～图4中可以看出：该林场的林木种内种间竞争强度与对象木的胸径大小之间呈幂函数关系，R2均大于0.5，拟合结果较为理想，对象木与竞争木的竞争指数之间模型的幂均为负值，表明对象木的个体胸径越大，距离对象木一定范围内的竞争木较少，竞争木对对象木竞争强度呈递减的趋势。4种竞争指数在不同样地中均随着胸径的增大而减小，其中胸径<15 cm时，对象木竞争指数随着胸径的增加急剧减小；当胸径>15 cm后，其减小的程度逐渐平缓。从拟合结果还可以看出，在3块样地中，简单竞争指数比综合竞争指数与林木胸径的拟合程度小，即C>H、Cm>Hm；修订后拟合的简单竞争指数和综合竞争指数与胸径的拟合度高于修订前，即Hm>H、Cm>C，显示了修订后综合竞争指数的优越性。

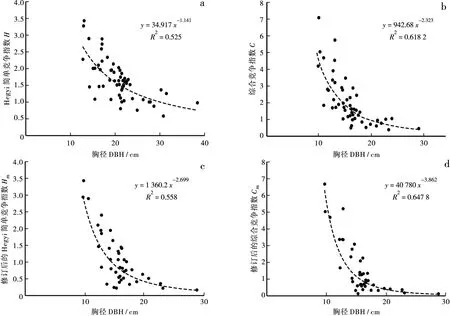
图2 1号样地不同竞争指数与胸径拟合的结果Fig.2 Fitting results of different competition indexes and DBH in sample plot 1

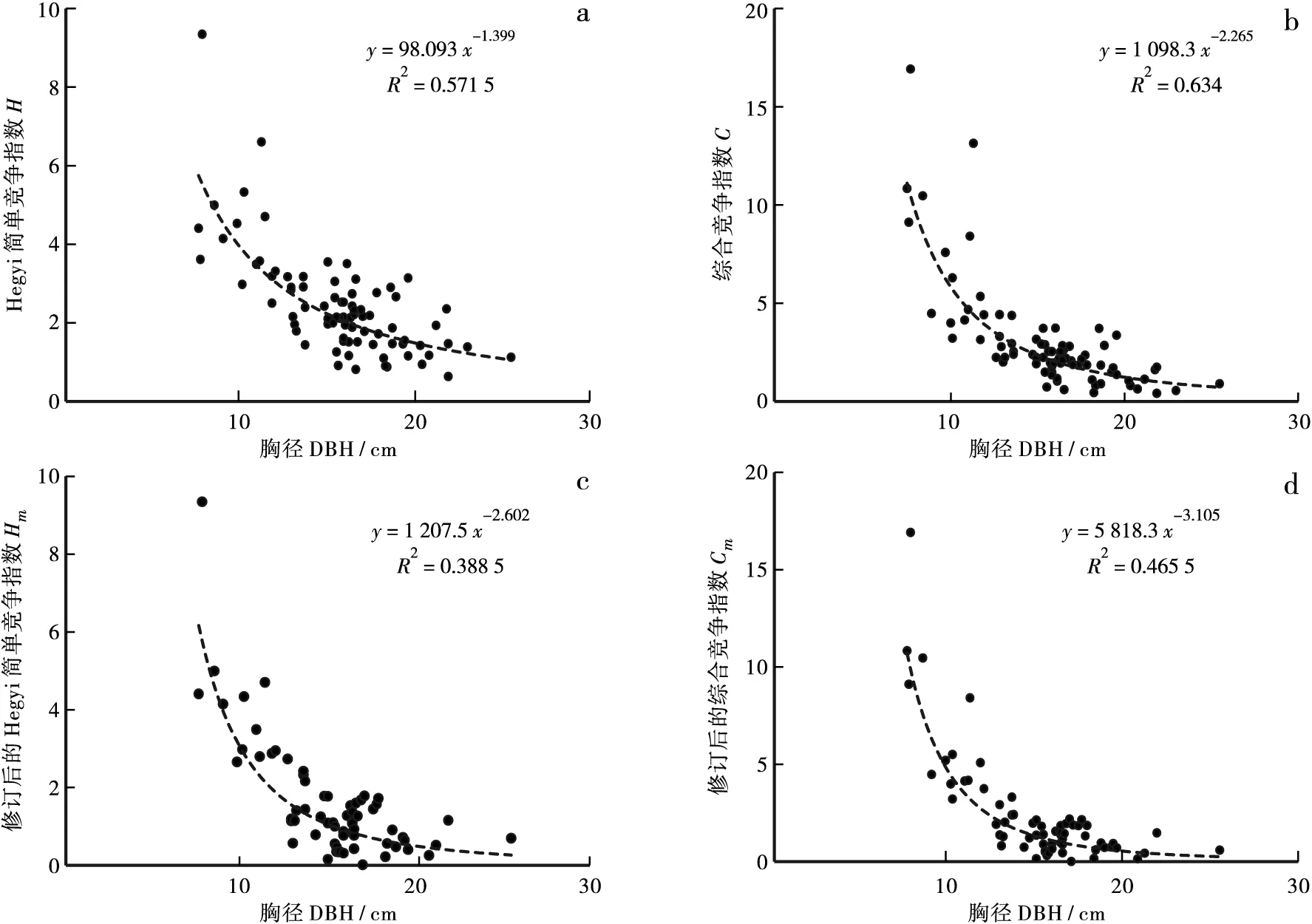
图3 2号样地不同竞争指数与胸径拟合的结果Fig.3 Fitting results of different competition indexes and DBH in sample plot 2

图4 3号样地不同竞争指数与胸径拟合的结果Fig.4 Fitting results of different competition indexes and DBH in sample plot 3

3.2.3 不同竞争指数平均值的分析

由图5可知：3块样地中不同竞争指数平均值的变化趋势均为C>H>Cm>Hm，其中修订前的2种竞争指数的平均值均大于修订后，即H>Hm，C>Cm。现在研究多集中于对称竞争，针对非对称性竞争研究较少，使得竞争指数平均值较大，忽略了处于竞争状态的林木间资源分配不均衡的问题。本研究考虑林木在同时争夺光照资源时，较高的林木比较矮林木更有竞争优势，结果显示修订后的综合竞争指数更适用于林木间的竞争情况。

图5 不同样地竞争指数平均值Fig.5 Average value of competition index in different plots

3.3 闽楠人工林种内种间竞争分析

表4反映了金洞林场闽楠人工林的3块样地内不同树种的种内、种间竞争情况。闽楠在各个样地内均有分布，3块样地中闽楠的种内平均竞争指数分别为0.53、0.54、0.81，种间平均竞争指数分别为0.53、0.83和0.99，种间平均竞争指数分别是种内平均竞争指数的1.00、1.54和1.22倍，说明闽楠在研究区内的种间竞争最为激烈，其种间竞争压力大于种内竞争压力。按不同树种分析种内平均竞争指数可知，1号样地中，阿丁枫>闽楠>木荷；2号样地中，木荷>闽楠；3号样地中，闽楠>杉木。以不同树种种间平均竞争指数为标准比较大小，1号样地中各树种的竞争强度为闽楠>木荷>阿丁枫；2号样地中，闽楠>香樟>木荷；3号样地中，闽楠>杉木。

表4 各样地不同树种的种内、种间竞争强度Tab.4 Intraspecificandinterspecificcompetitionintensityofdifferenttreespeciesindifferentgroups样地号树种种内竞争种间竞争株数竞争指数平均竞争指数株数竞争指数平均竞争指数闽楠(Phoebebournei)5227.300.53189.600.531木荷(Schimasuperba)2411.400.48233.140.14阿丁枫(Altingiachinensis)53.800.76211.800.09闽楠(Phoebebournei)5831.400.545142.200.832木荷(Schimasuperba)5649.900.895239.400.76香樟(Cinnamomumcamphora)———43.200.803闽楠(Phoebebournei)6855.200.815150.400.99杉木(Cunninghamialanceolata)4823.600.496446.000.72 注:“—”表示该树不存在种内竞争。

4 结论与讨论

目前已有的竞争指数模型中，众多学者在Hegyi[9]竞争指数模型基础上提出了不同的竞争指数模型来描述林木之间的竞争强度，综合考虑胸径、树高、冠幅和林木距离等与林木竞争的关系。林木在争夺光照资源时，较高的林木比较矮林木更有优势[23]，所以本文在选取简单竞争指数和综合竞争指数的模型时进行了修订，修订后的模型中剔除了比对象木矮的竞争木。

本研究分析了金洞林场闽楠人工林3块样地内修订前与修订后的简单竞争指数和综合竞争指数与林木胸径的Pearson相关系数为负值(P<0.01)，且均与胸径呈幂函数关系，所有模型的次幂值均为负值，Pearson相关系数的绝对值表现出综合竞争指数高于简单竞争指数，且修订后的简单竞争指数和综合竞争指数均高于剔除前，修订后的综合竞争指数的绝对值最大。3块样地中的不同竞争指数的平均值排序均为C>H>Cm>Hm，且各个样地内修订之后综合竞争指数与胸径拟合后R2均为最大，分别为0.742 9，0.809 4和0.701 7，说明修订之后综合竞争指数更能准确地表现林木间的竞争程度，这与褚欣等[17]以闽楠天然次生林为研究对象提出的综合竞争指数，及吕勇等[24]基于湖南岳阳市芦头林场青冈栎(Cyclobalanopsisglauca)次生林为研究区，构建考虑竞争木冠幅重叠面积的竞争指数结果相似，与Weiner[18]、Pretzsch等[20]将模型中比对象木矮的竞争木剔除，修订后的综合竞争指数模型和简单竞争指数模型比修订前结果更优的结果相吻合。基于此，将弥补模型修订前忽略的较高的林木比较矮林木更有优势的缺陷。

基于修订后综合竞争指数模型计算各样地间林木竞争强度，研究表明在金洞林场闽楠人工林样地内，1号样地与2号样地内对象木有3种，3号样地内对象木有2种，其样地内株数分布较为均衡，对象木的胸径分布呈现两头少中间多的分布特征，其平均胸径主要集中在11.0～19.0 cm间，林木的胸径为15.0 cm以上时，竞争趋势逐渐趋于平缓，竞争压力明显减小。段仁燕等[12]以天柱山为研究区，对黄山松(Pinustaiwanensis)的种内、种间竞争强度进行深入研究，结果表明竞争指数在对象木胸径达到20.0 cm之后几乎没有变化，应在对象木胸径达到20.0 cm之前采取相应的人工抚育间伐措施，减少林分密度过大对林木正常生长造成的影响，减少对象木的竞争压力[25]。因此，为了促进金洞林场闽楠人工林的合理经营，应在对象木胸径大小达到15.0 cm之前制定合理的抚育间伐方案。在3块样地中，闽楠树种平均种间竞争指数大于种内平均竞争指数，说明闽楠树种的竞争压力主要来自于种间竞争。这些研究结果对金洞林场闽楠人工林的抚育间伐木的确定及间伐强度的确定都有一定的指导意义。