基于多目标粒子群优化的同心圆环阵列方向图综合算法
王新宽,王桂宝,黄朝军,熊召新
(陕西理工大学 物理与电信工程学院,陕西 汉中 723001)
0 引 言
同心圆环阵列天线(concentirc ring antenna array, CRAA)的天线单元均匀分布在以口径中心为圆心的一系列同心圆环上,其特点是可以产生绕方位角旋转对称的方向图,从而被应用在无线电测向、声呐、导航[1]、雷达、射电天文、卫星通信等领域[2-3]。针对CRAA的方向图优化方案主要包括确定性算法[4-6]、智能优化算法[7-12]及一些结合智能优化算法的混合设计方案[13-14],其中又以基于后两类算法的设计最为普遍。典型工作包括:文献[6]根据第1类贝塞尔函数的特性,实现了一种具有低旁瓣、宽带特性和大角度扫描功能的CRAA;文献[7]利用遗传算法(genetic algorithm, GA)对CRAA进行了优化;文献[8]提出了一种基于修正GA的降维优化方法,把二维阵列的优化降维成一维直线阵来降低算法的复杂度;文献[9]利用一种修正实数编码遗传算法(modified real genetic algorithm, MGA),通过优化圆环半径来抑制峰值旁瓣电平;文献[10]提出了一种改进的整数遗传算法(improved integer genetc algorithm, IIGA),通过对编码、交叉、变异等策略进行改进,使算法能以较少的运算负担,收敛到满意解,且可应用于优化单元数达上千的阵列;文献[11]把迭代傅里叶变换(iterative Fourier transform, IFT)和差分进化算法(differential evolution, DE)结合起来,应用于降低圆平面阵列的旁瓣电平,该算法能够较大程度缩减DE的寻优空间,具备较快收敛的特点;文献[12]应用粒子群算法(particle swarm optimization, PSO),对圆平面阵列的单元数及口径尺寸进行优化,降低了波束宽度和旁瓣电平。除此之外,文献[13]提出的混合策略(hybird strategy, HS)、文献[14]基于布谷鸟搜索的算法,均可有效抑制不同口径CRAA的旁瓣电平。
以GA为代表的智能优化算法,因其良好的鲁棒性、自学习性、内在的并行性等特点,在CRAA及各种其它阵列[15-17]的方向图优化中得到了广泛应用。然而,此类算法仅限于优化单元数和口径较小的阵列。对单元数达上千的大型阵列,个体变量的增加导致搜索空间急剧扩大,再加上初值的随机性,使得算法需要大量的迭代(对应相当大的计算负担)才可能收敛,甚至完全无法收敛。尽管文献[10,13]对部分大口径CRAA进行了优化,但并未给出具体的计算耗时,所得结果也非最佳结果。除此之外,绝大部分文献都以降低CRAA的旁瓣电平为单一目标,并未考虑到优化其方向性系数(方向性系数的提升有助于增加阵列主辐射方向的灵敏度和覆盖范围),通常会导致阵列方向性指标的下降。
基于上述考量,以及单元密度呈锥削分布有助于抑制阵列旁瓣的思想,本文提出了一种新的密度锥削策略(new density tapering strategy, NDT),并把它和多目标粒子群算法[18-19](multiple objective particle swarm optimization, MOPSO)结合起来,形成一种涵盖各种口径CRAA,能同时优化其旁瓣电平和方向性系数的多目标、全局优化方案—NDT-MOPSO。传统的密度锥削策略(density tapering strategy, DT)[20-21]常需借助一些已知的连续激励源(比如泰勒连续源)作为参考来确定单元分布,与之不同的是,在NDT中,通过引入圆环填充因子作为优化变量来调整CRAA中不同圆环上的单元数目,只需对圆环的填充因子加以适当约束,就可确保单元分布在总体上呈密度锥削状态,极大增加了单元放置的灵活性。而且,圆环填充因子的引入有助于把同一圆环上单元放置的数目转化为(0,1)的实数,使得在优化过程中只需采取统一的实数编码,极大简化了个体变量的编码方式,也把不同圆环上对单元个数及单元最小间距的强约束问题,转化为只需考虑该圆环上填充因子上、下限的无约束问题,降低了算法的复杂度,有利于算法的快速收敛。具体来说,受到超低副瓣泰勒阵列(该阵列的特点是口径中心附近单元的归一化电流激励值均接近于1,靠近口径外围的单元激励依次减小)的启发,NDT-MOPSO在阵列口径上划分出一些半径不同的同心圆环,并确保在算法的每一次迭代中,位于口径中心附近、约占总数一半的圆环始终处于满阵填充状态,而对剩余靠近口径外围的圆环,使圆环间距均大于半波长且以随机方式从内向外依次增加,并限定它们的填充因子变化范围处于两个随圆环半径的增加缓慢减小的门限之间,从而确保在优化过程中,单元放置始终满足密度锥削分布。把阵列口径进行上述划分并确定好外围圆环填充因子的变化范围后,以单元最小间隔、外围圆环之间的间距及其填充因子组成待优化的个体向量,以低旁瓣、高方向性系数作为优化目标,利用MOPSO算法进行优化以寻找可行的Pareto最优解。仿真结果表明,由于在算法前半部分采取了NDT策略,使得在优化过程中能够始终用一些高质量的解来约束和指导MOPSO中个体粒子的进化,最大程度避免了算法陷入随机搜索的可能,使算法能以较小的种群规模、较少的迭代次数,收敛到可行的Pareto最优解。
1 同心圆环阵列模型
设CRAA由一个位于口径中心的单元和分布在L个同心圆环上的天线单元共同组成,圆环编号按照从内向外的顺序依次记作l=1,2,…,L,且把第l#圆环的半径及其填充单元总数分别记作rl、Nl。同心圆环阵列示意图如图1所示。在所有单元均为等幅激励的全向单元情况下,CRAA的方向图函数为[7]
(1)
(1)式中:k为波数,n=1,2,…,Nl,依次表示l#圆环上,从y轴正半轴算起,沿逆时针方向的单元编号;(θ0,φ0)表示l#圆环上第n个单元的编号,φl.n代表该单元的角位置;u、v为正弦空间变量且满足u=sinθcosφ,v=sinθsinφ,θ和φ分别对应天顶角与方位角。若CRAA的主瓣指向(θ0,φ0),则u0=sinθ0cosφ0,v0=sinθ0sinφ0。据此,CRAA的最大方向性系数可表示为[22]
(2)
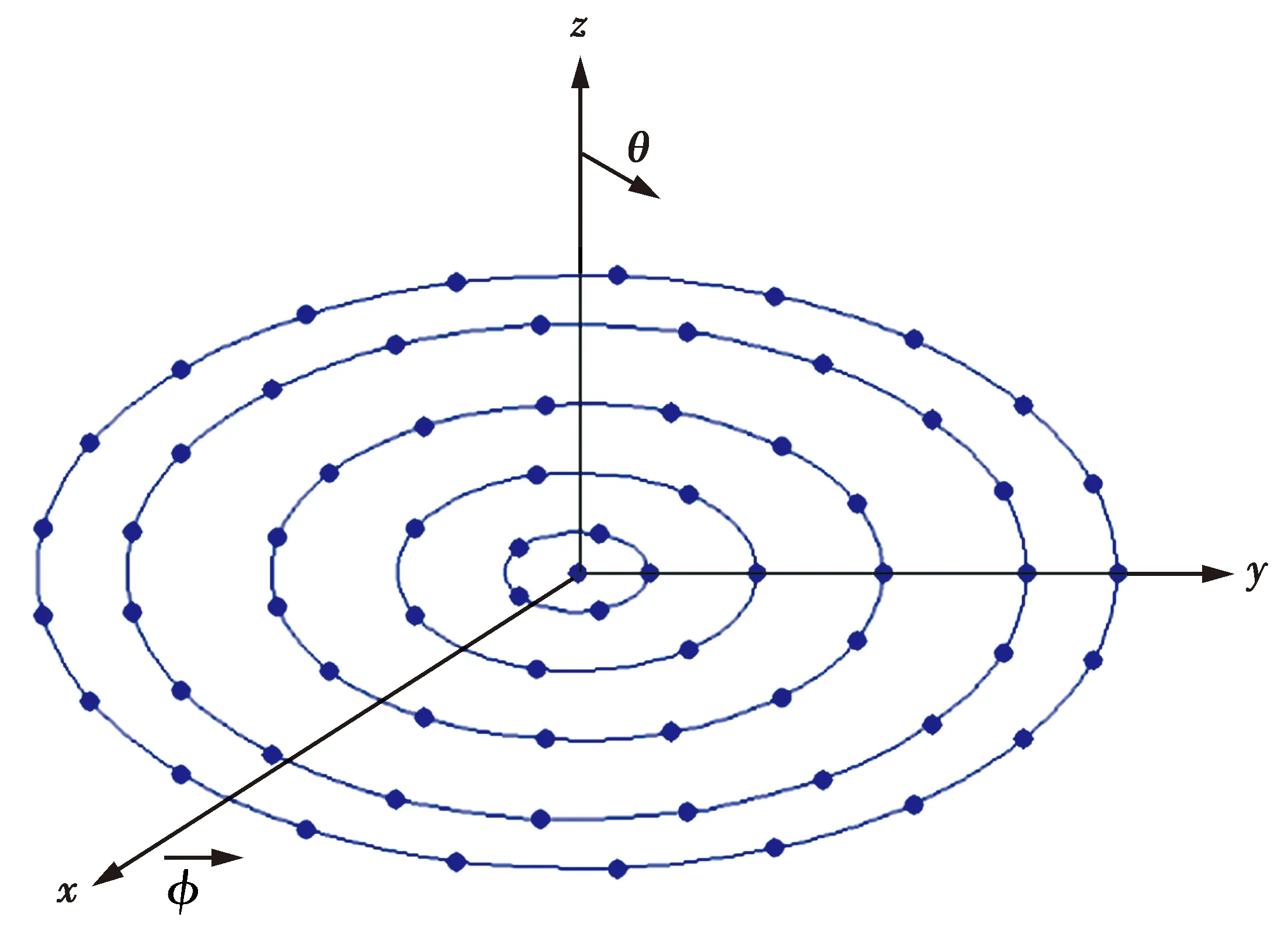
图1 同心圆环阵列示意图Fig.1 Schematic diagram of CRAA
若把CRAA旁瓣区域内所有峰值点坐标记作集合S,该阵列的最大旁瓣电平(简记为旁瓣电平)可表示为
(3)
根据(2)—(3)式,建立二维目标函数向量[SLL,D0],以下将利用MOPSO算法[19],并结合一种新的密度锥削策略NDT,实现对CRAA的旁瓣电平和方向性系数的协同优化。
2 算法步骤
如前所述算法的构造思想,假定CRAA的口径半径等于R,圆环数为L,把波长记作λ,并定义口径余量δ,表示为
δ=R-L·0.5λ, s.t.δ≥λ
(4)
据此,算法详细步骤如下。
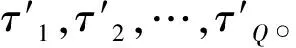
(5)
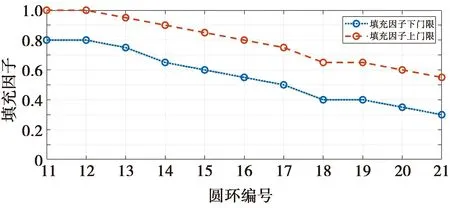
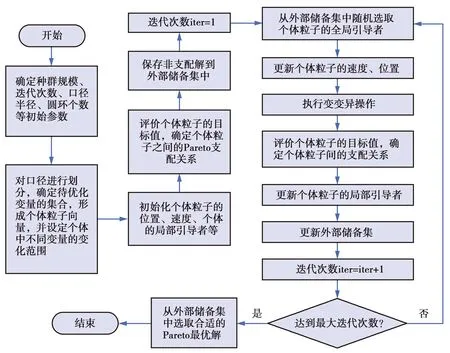
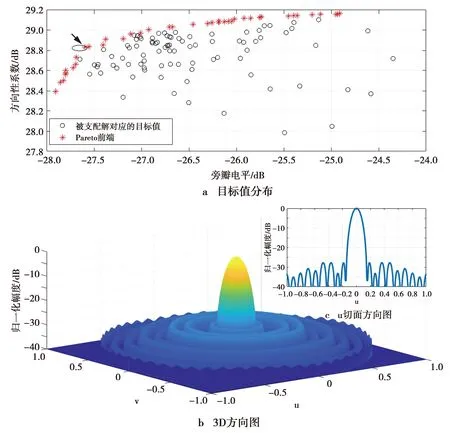
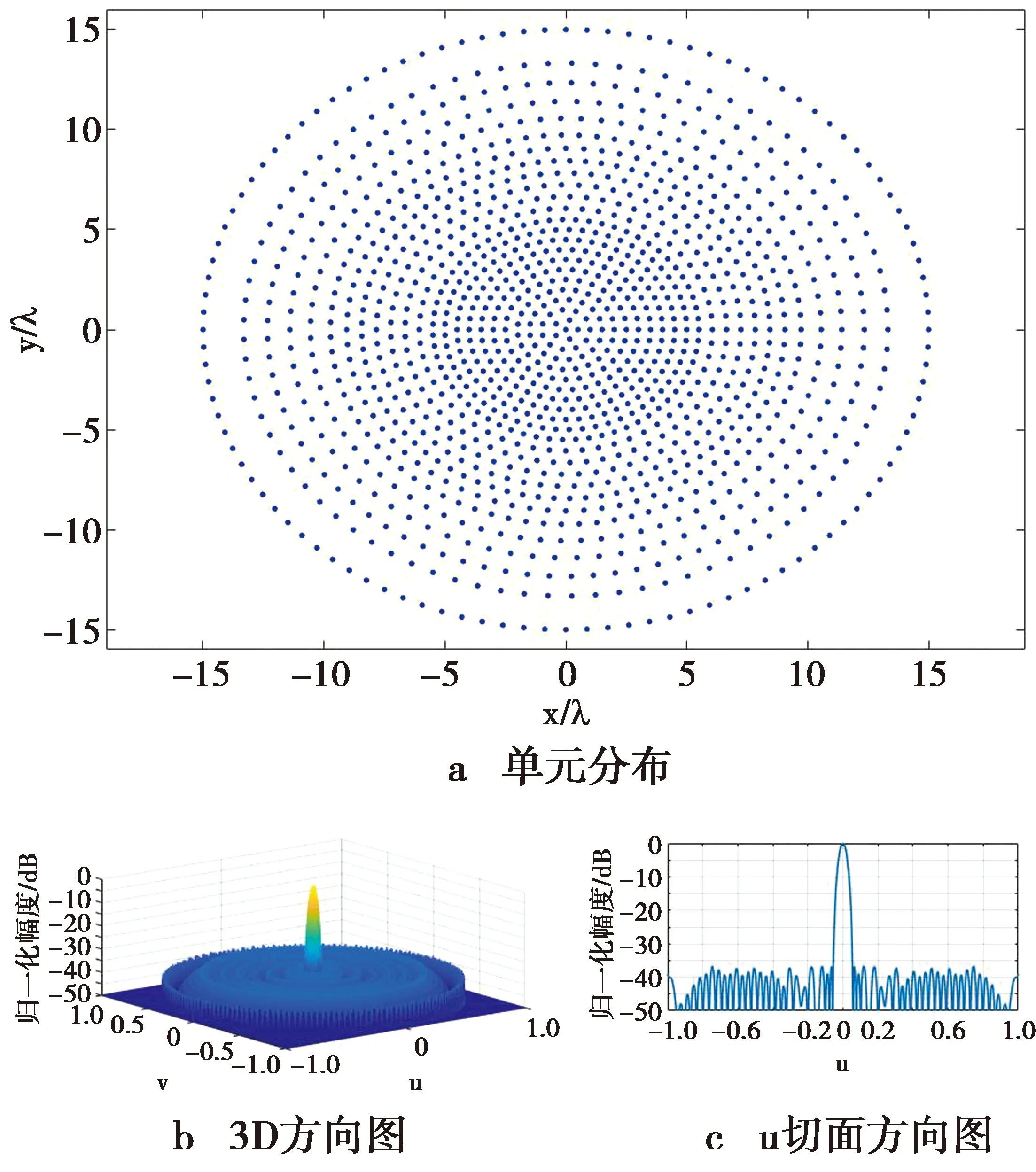
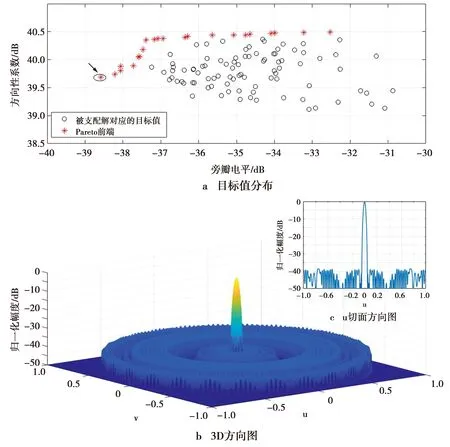
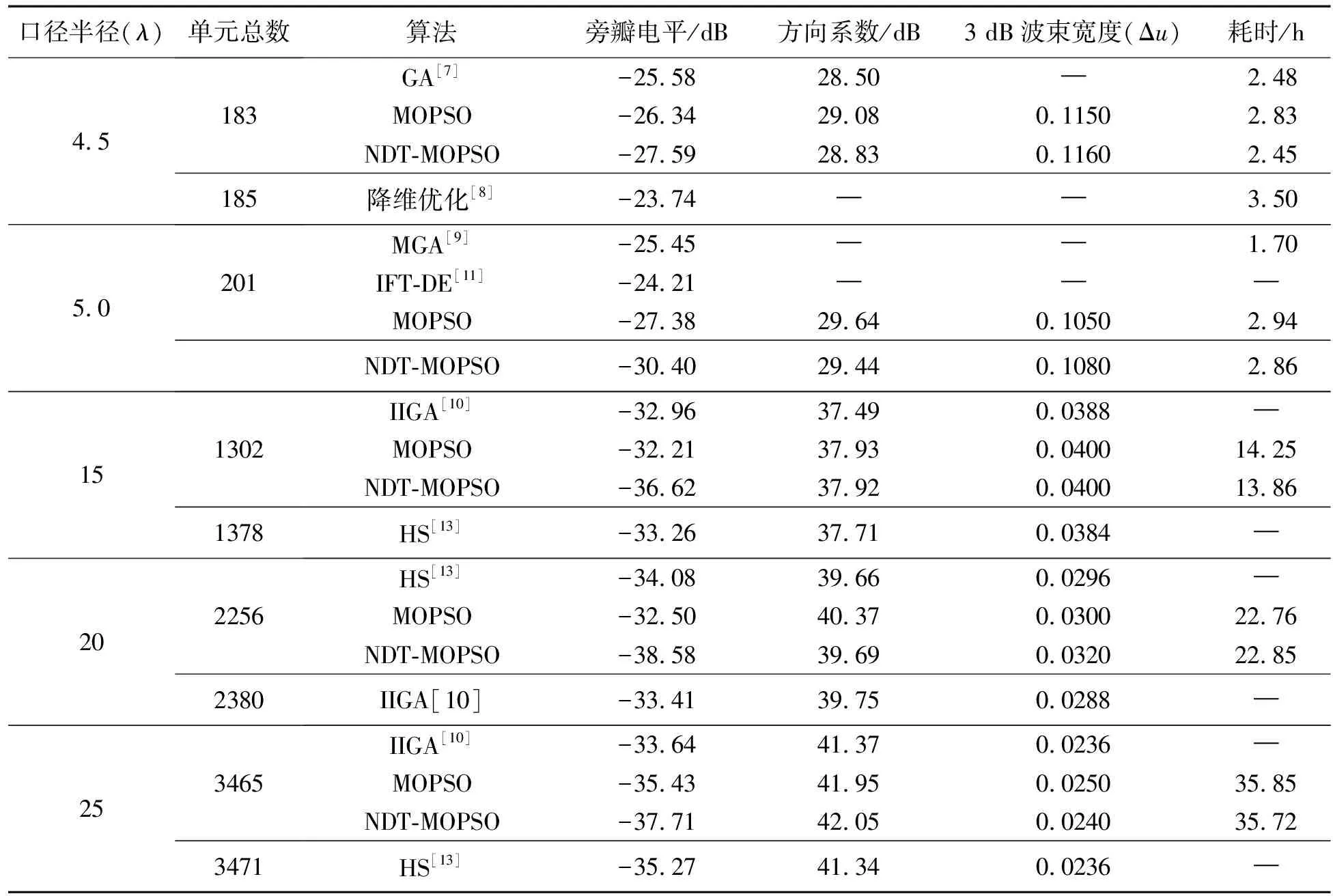
根据(5)式,外围圆环的半径rl,l0 rl0+q=(l0+q)·0.5λ+Δrq,q=1,2,…,Q (6) 把口径进行上述划分后,约占总数一半的内部圆环均以半波长为间隔,外围圆环的间隔均大于半波长且随圆环半径的增加逐渐增加。 (7) 相应地,可得 (8) ξ={d,τ1,τ2,…,τQ,f1,f2,…,fQ} (9) 向量中不同变量的变化范围需满足 (10) 3)基于MOPSO的优化。作为从PSO衍生出来的多目标进化算法,MOPSO继承了PSO算法的特点。粒子在飞行过程中,需要不断跟踪并更新粒子个体以及粒子群体迄今为止的历史最优解来决定其下一步的飞行方向和距离[18-19]。由于PSO通常处理的是单目标问题,故在每次迭代中,群体的历史最优解是单一的,算法终止后的输出结果也是单目标下的最优解。与之不同的是,MOPSO算法中,历史最优解不再单一,而是一组Pareto最优解,这些最优解是互不支配的非支配解。为此,引入外部储备集,把一定数目的非支配解放入该储备集中,作为群体的历史最优解集。在算法的每次迭代中,从外部储备集中随机选取一个解作为历史最优解用以指导粒子的飞行,并在该次迭代结束后更新储备集。当算法结束后,输出结果是一组互不支配的Pareto最优解集,可根据不同目标的需求选择合适的非支配解。图3给出了本算法的流程图。 图2 圆环数为21的CRAA,待优化圆环的填充因子 变化范围示意图Fig.2 Schematic diagram describing the variation ranges of filling factors for the rings waiting to be optimized, for a CRAA including 21 rings 图3 NDT-MOPSO算法流程图Fig.3 Flow chart of the NDT-MOPSO 设定算法的种群规模和迭代次数均为100,储备集大小等于50。为对比说明算法的性能,建立的CRAA模型具有和文献[10,13]相同的口径与单元数。假定阵列的口径半径等于4.5λ,单元总数183,圆环数为8(按照从内向外的顺序依次标记为1#-8#圆环)。依据本算法,经过优化后,在所得CRAA内部,由1#-4#圆环形成圆环间距为0.5λ的满阵结构,这些圆环上填充的单元数依次等于6、12、18和25。扣除掉口径中心的一个填充单元,则处于外围的5#-8#圆环需要填充的单元总数为121。根据前述算法步骤,这4个圆环的填充因子均需在由(10)式设定的范围内随机给定,然而这样无法确保单元总数等于预设值的要求。为此,只把5#-7#圆环的填充因子设置为随机的,并把它们对应的填充因子下限依次置为0.8、0.6和0.5。根据(8)式,与之对应的填充因子上限分别等于1.0、0.85和0.75。这样,在算法的每次迭代中,处于最外围的8#圆环填充单元的数目等于预先确定的单元总数减去该阵列已经填充的单元数,从而满足了单元总数等于预设值的要求。最终得到的阵列具有-27.59 dB的旁瓣电平和28.83 dB的方向系数。对比文献[7]的结果,旁瓣下降约2 dB,方向系数提升了0.33 dB。对比文献[8],旁瓣下降了3.85 dB。 图4给出了算法的优化结果。其中,图4a描述了经过100次迭代后,得到的Pareto前端和被支配解对应的目标值分布情况,箭头所指为本例中选取的Pareto前端解。图4b、图4c依次给出了该阵列的3D方向图和u切面方向图。类似地,当口径半径等于5.0λ,单元总数为201时,所得CRAA的旁瓣电平降至-30.4 dB,方向系数上升到29.44 dB。与文献[9,11]的结果相比,旁瓣电平分别下降了4.95 dB和 6.19 dB。 图4 单元数等于183的CRAA优化结果Fig.4 Optimization results for the CRAA with the number of elements equal to 183 当阵列的口径半径等于15λ,单元总数为1 302时,优化结果如图5所示。该阵列的旁瓣电平和方向系数分别为-36.62 dB和37.92 dB,与文献[10]中基于IIGA的结果相比,旁瓣下降3.66 dB,方向系数提升0.43 dB。与采用HS[13]的结果相比,在单元总数减少76的情况下,旁瓣降低约3.36 dB,方向系数提升0.21 dB。类似地,若把阵列的口径半径提升至20λ,填充单元数增至2 256,基于本算法的优化结果如图6所示。图6a箭头所指的Pareto前端解,对应的旁瓣电平为-38.58 dB,方向系数等于39.69 dB,与HS[13]的结果对比,在方向系数几乎不变情况下,旁瓣降低约4.5 dB。对比IIGA[10]的结果,在单元数减少124,方向系数基本不变情况下,旁瓣电平降低了5.17 dB。 图5 单元数等于1 302的CRAA优化结果Fig.5 Optimization results for the CRAA with the number of elements equal to 1 302 从图6a所示的Pareto前端可进一步看出,为获取更高的方向系数,可选取旁瓣电平在-37 dB左右对应的非支配解。当阵列的口径半径等于25λ,填充单元数为3 465时,得到的CRAA具有-37.71 dB的旁瓣电平,以及42.05 dB的方向系数。对比IIGA[10]的结果,旁瓣下降4.07 dB,方向系数提升0.68 dB,与HS[13]的结果相比,旁瓣下降2.44 dB,方向系数提升0.71 dB。表1列出了不同算法的对比结果,并且为说明采取NDT策略初始化后带来的优越性,同时给出了仅采用MOPSO算法的运行结果。可以看出,与MOPSO及其它算法相比,采用NDT-MOPSO算法进行优化后,不同口径CRAA的旁瓣电平下降在1.25~6.19 dB。以上所有运行结果均在处理器为Intel i5-6500,内存4GB,Windows 7操作系统的PC上完成,编程语言采用MATLAB,不同算例运行时间在2.45~35.85h。 图6 单元数等于2 256的CRAA优化结果Fig.6 Optimization results for the CRAA with the number of elements equal to 2 256 表1 口径不同时几类算法的对比结果 通过把阵列口径划分为一些半径不同的同心圆环,在单元最小间距约束下,选取约占总数一半的圆环,以半波长为间隔,在靠近口径中心处形成满阵结构。然后,对剩余靠近口径外围的圆环,使其间距随机分布但始终满足从内向外依次增加且大于半波长的条件,并限定这些圆环的填充因子在两条随圆环半径的增加缓慢下降的门限曲线之间。这样,确保在优化过程中,单元放置始终呈锥削分布,最大程度避免了算法陷入随机搜索的可能。并且,圆环填充因子的引入也简化了编码方式,降低了单元放置的约束条件,有利于算法的快速收敛。仿真结果表明,与现有的几类算法相比,NDT-MOPSO适用于优化各种不同口径的CRAA,能在相近的机时下,大幅降低CRAA的旁瓣电平,并保持较高的方向系数。需要说明的是,算法初始阶段对圆环个数的选取并不是随意的,而是经过少数几次数值试验,使阵列具有较低的旁瓣电平即可。并且,也可以不预设单元数目进行优化,这样有可能在同等指标下,降低阵列的填充单元数量。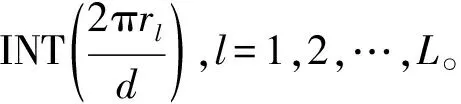
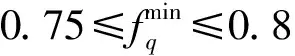
3 数值仿真及结果分析
4 结 论

