丰富情境 加强『回顾反思』教学
——《归总问题》素养进阶习题展评与教学建议
文|宋煜阳 楼蔚波
一、习题展评
●习题一
1.习题内容。
每行有12 人,可以排6 行。如果这些人排成9 行,每行有多少人?
(1)选一选,下面哪幅图能表示题目的意思?( )
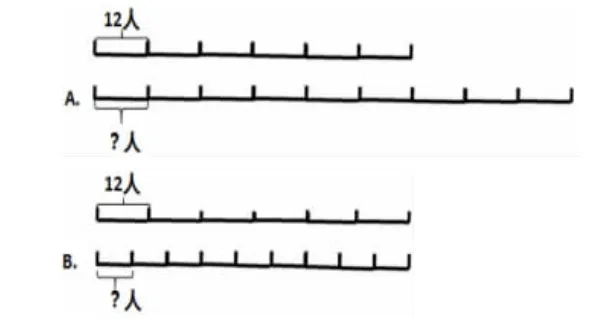
(2)我能列式计算。
(3)我的检验过程。

(4)想一想,这些人还能怎么排队呢?
可以排成( )行,每行( )人,我的算式:_______________。
2.能力指向。
指向解决问题的关系分析与表征、过程设计与执行、结果反思与评价三个维度考查。具体包括用线段图表达数量关系,理解解决问题方案和算式的意义,能对结果的正确性与合理性做出反思与评价,并开放性地提出条件和列式解答。
3.学情分析。
后测对象为城区小学45 名学生。学生在图意选择和列式计算方面总体表现不错,个别学生在开放性提出条件和列式练习中不能正确作答。最为薄弱的是按要求检验,约20%的学生虽然进行了检验,但检验方法采用了除法检验“72÷8=9”、再算一遍检验“72÷9=8”、看图等,不符合题目要求的“通过计算总人数是不是相等”进行检验;超过10%的学生不知道怎样检验。
●习题二
1.习题内容。
小亮生病了,医生为他开了一盒药。

(1)根据算式提出问题。
18×3=54(片)
_______________
18÷6=3(天)
_______________
(2)这些药够吃几天?
2.能力指向。
指向信息获取与解读、过程设计与执行等能力。主要表现为信息梳理、关系分析、列式解答等过程是否清晰、合理有序。
3.学情分析。
从数据看,学生对第一个算式的意义解读得比较准确,对第二个算式意义的解读存在困难,提问也不够准确。在解决“这些药够吃几天?”问题时,学生有的无法获取信息,有的不知道总数应如何进一步分配。
●习题三
1.习题内容。
如图,小亮用小棒搭了9 个三角形,相邻的两个三角形都有一条公共边。现在用同样多的小棒搭正方形,如图,相邻的两个正方形同样有一条公共边,可以搭几个这样的正方形?

2.能力指向。
考查学生运用模型解决问题能力,在数形结合问题中发现图形排列的规律。
3.学情分析。
根据学生在解决问题时的具体表现,划分4 个水平等级,具体如下表(表格见文末)。
测试班级80%的学生停留在水平0 和水平1,达到水平3 的仅占6.7%。超过40%的学生没有得出小棒总数、无法正确解读“公共边”信息,没能发现图形排列的规律;另有近40%的学生只得出小棒总数,包括部分学生是数出来的,无法进一步解决问题。
二、教学建议
1.丰富情境类型,充分经历归总问题模型形成过程。
测试班级在练习一、练习三形成较大反差,主要原因是学生对情境的熟知程度直接影响了问题解决。其中,练习一属于学生熟悉的生活情境,较为充足的生活经验支持学生对总量的提取;练习三属于数学情境,相对抽象程度较高,学生不易提取总量不变的特征。这也反映了归总模型并没有完全建立。为此,教学中一方面要丰富情境,提供生活情境、社会情境和数学情境,让学生全面感知问题;另一方面要善于从各类情境中抽象提炼,通过题组比较、寻找共性,帮助学生归纳出此类问题“总量不变”的特点和数量关系分析方法,形成归总模型。
2.重视回顾反思,开展多元检验方法的训练。
回顾反思是解决问题的重要环节。实际教学中,许多教师不大重视回顾反思环节的落实与常态训练,导致学生解决问题后检验的意识不强,更谈不上检验习惯的养成。因此,建议教学中要有意设计“回顾与反思”的专项练习,包括解读他人检验方法合理性、提出新的数学问题等相关练习。
人教版教材解决问题的例题都编排了“回顾与反思”环节,但回顾与反思的方法有所侧重,需要进一步梳理检验方法,开展多种方法检验的训练。归总问题重在用总量是否不变的方法进行检验;归一问题可以用单一量不变、份数是否相同等多个角度进行检验。实际教学中,学生检验意识不强、习惯于用“再算一遍”的检验方法,需要教师对检验方法进行归类并组织必要的训练,帮助学生学会检验、优化检验方法。


