基于SQSWOMP算法的轴承实时故障诊断研究*

钱子君,吴 波,于剑峰,王文瑞,王振明,袁晓兵

（1.中国科学院 上海高等研究院,上海 200120;2.中国科学院大学,北京 100089;3.中国科学院 上海微系统与信息技术研究所,上海 200233）

0 引 言

随着工业的发展,旋转机械设备逐渐向精密化、自动化、智能化方向发展[1]。旋转机械设备通常包含轴承系统、变速系统、转子、联轴器,高度结构化使得其内部组件之间的联系更加紧密,对设备运行可靠性的要求也更高。旋转机械设备工作环境恶劣复杂,长期高强度工作增加了其故障频发的可能性,重则会造成人员、财产的重大损失[2]。

滚动轴承作为重要的传动和承托零件,是旋转机械设备的重要组成部分。

轴承故障通常表现为内、外圈和滚动体的局部损伤,如表面出现裂纹、磨损或者剥落等,故障发生比例高达30%[3]。轴承一旦失效,旋转机械设备工作状况会逐渐恶化,直至无法工作。所以对轴承的状态进行监测是保障复杂旋转机械设备安全性与稳定性工作的关键之一。根据监测结果可以确定合理的检修时间,制定适宜的维修方案,因此,对滚动轴承进行实时状态监测和故障诊断具有极大的工程意义。

滚动轴承故障诊断主要步骤为:（1）信号采集;（2）故障特征提取;（3）故障监测分类。

在轴承故障诊断方法中,最早、最成熟的是振动分析法。比如,短时傅里叶变换[4]、经验模态分解（empirical mode decomposition,EMD）[5]、小波变换法[6]等。短时傅里叶变换在提取信号的非线性特征时,由于窗函数固定,导致时频分辨率无法改变;EMD可以将振动信号自适应分解,但可能出现端点效应、模态混淆等问题;小波变换法对小波基的选取敏感性大,时频域精度有待改进。

随着计算机技术的发展,由于人工智能算法具有强大的非线性信号特征提取能力,被广泛应用到故障诊断中。常见的故障分类算法有:BP神经网络[7]、支持向量机（support vector machine, SVM）[8]、K最邻近算法（k-nearest neighbor, KNN）[9]130-131等。这些算法都存在一定的局限性。比如,BP神经网络会出现过拟合、收敛困难等问题;SVM的故障分类效果受到数据样本分布与参数选取两方面影响[10];面对海量实时采集的轴承数据时,KNN算法的效率有待提升。

皮骏等人[11]用改进的遗传算法优化了BP网络的权值和阈值,对滚动轴承正常、内圈故障、外圈故障和钢球故障4种工况进行了诊断。张弛等人[12]将轴承振动信号输入二维卷积神经网络,进行了自适应特征提取,再取全连接层结果作为支持向量机的输入,实现了对轴承的故障分类。王嘉浩等人[9]129-133在KNN中引入了相似度量,并且结合小波包分解算法,对轴承故障进行了诊断。

当处理振动信号的分类问题时,单一的模型无法准确地识别轴承故障,这些分类算法需要结合其他降噪算法,并寻找最优参数,庞大的数据量会消耗大量计算资源,难以实现实时的故障诊断,且很少关注到信号采集存储方面的问题。

压缩感知理论是在信号稀疏分解和近似理论的基础上发展起来的一种新的信号处理理论[13],它避免了传统奈奎斯特定理的局限性,实现了边采样、边压缩,节省了振动信号的获取时间与存储传输成本,并被成功应用于图像和故障诊断等许多领域。

郭俊锋等人[14]提出了基于K-SVD字典学习算法,稀疏表示振动信号压缩测量的重构方法,通过研究离散余弦（discrete cosine transform, DCT）字典的方式,用振动信号训练得到了特定字典,发现了用振动信号训练成的字典稀疏表示性能优于固定字典。鹿洪荣[15]提出了一种基于压缩感知理论的机械故障信号检测方法,用压缩感知理论构造了测量矩阵,并用范数稀疏逼近法求稀疏解,其故障诊断准确率可达到96.16%。ZHANG Xin-peng等人[16]1253-1265提出了基于K-奇异值分解（k-singular value decomposition, K-SVD）与正交匹配追踪算法（orthogonal matching pursuit, OMP）的低维信号故障诊断方法,并研究了观测值对其性能的影响。

上述文献中,K-SVD算法的稀疏编码算法均采用OMP算法,而OMP算法需要信号稀疏度作先验知识,对测量矩阵也有一定的要求。

作为常见的信号重构算法,贪婪算法包含OMP[17]、子空间追踪算法（subspace pursuit, SP）[18]、稀疏度自适应匹配追踪算法（sparsity adaptive matching pursuit, SAMP）[19]、分段弱正交匹配追踪算法（stagewise weak orthogonal matching pursuit, SWOMP）[20]等。OMP算法在每次迭代过程中均需求解目标函数的最小二乘解,其重建的复杂度较高。SP算法引入回溯思想,可以获得更好的重建质量和较低的重建复杂度,但需要将稀疏度作为先验知识,因此,难以将其应用到未知的复杂振动信号特征提取问题上。SAMP算法的重建精度仍有上升空间,其重建效率低的特点使它很难实现故障的实时监测。SWOMP算法不需要将稀疏度作为先验条件,减少了对测量矩阵的要求,在重建信号时,SWOMP算法采用内积准则,从传感矩阵中挑出与残差信号较为匹配的原子;在迭代过程中,使用固定的阈值参数极易导致高估或低估的结果;并且由于在迭代过程中寻求的不是最优解,导致了SWOMP算法重建精度较低。

近些年来,也有很多关于改进贪婪算法的研究。张瑞等人[21]提出了一种改进的OMP算法,用共轭梯度法对OMP算法中的直接矩阵求逆步骤进行了改进,降低了算法的复杂度。贺绍琪等人[22]在测量矩阵方面对SWOMP算法进行了改进,用部分哈达玛矩阵替代了传统的高斯矩阵,显著降低了测量矩阵的互相关性,提高了其重建精度。刘建生等人[23]利用广义Jaccard系数相似性的匹配准则代替了内积匹配准则,解决了以内积准则求向量相似度造成原子丢失的问题,优化了原子筛选过程。

针对SWOMP算法的不足,笔者提出一种S形二次分段弱正交匹配追踪算法（s-shaped quadratic stagewise weak orthogonal matching pursuit, SQSWOMP）。

首先,笔者基于S形函数有初始阶段快速接近、最终阶段缓慢接近的变步长特点,在SWOMP算法中引入S形变换函数,使得每次迭代得到的门限参数根据重构误差有所调整,以解决SWOMP算法对门限参数的选取依赖性大的问题,提高算法的自适应性;并且在SWOMP算法的原子选择过程中,根据回溯思想,加入原子的二次筛选过程,剔除无效原子,提高算法的重构精度;将SQSWOMP算法应用到K-SVD算法的稀疏编码阶段中,以期提高故障特征信息的提取能力,有效识别出轴承信号的状态。

1 压缩感知理论

压缩感知理论表明,如果信号具有稀疏性,那么可以通过与变换不相干的观测矩阵,将原高维信号投影至低维空间,再经过重构算法,就可以实现用低维信号精准地恢复原始高维信号。

但信号通常在时域上是不稀疏的,需要做相应的变换以实现信号的近似稀疏。例如,某些时域不稀疏的信号在频域是稀疏的,通过傅里叶变换将原信号转换为频域信号,这一步即代表信号的稀疏表示,继而通过重建方法在稀疏域复原出原信号。

压缩感知理论的3个核心问题是信号观测、稀疏表示与信号重构,如图1所示。

机械设备是由不同组件构成的高结构化整体,需要的设备监测点较多,长时间、持续的监测会生成海量数据,这给数据存储、传输带来了巨大压力。旋转机械设备工作环境复杂恶劣,采集到的原始数据中包含的并不都是有用信息,如果直接存储、传输原始数据,会导致资源的浪费。压缩感知理论只需较少采样值,就可以不失真地重构原始高维信号,这大大减少了对轴承数据采集时间与硬件资源的浪费,减轻了数据的存储、传输压力。

由于机械设备工作环境恶劣、复杂,轴承信号具有数据量大、噪声强、高维度的特点,单一人工智能模型无法准确地识别轴承故障,这些分类算法需要结合其他降噪算法,并且寻找最优参数,庞大的模型参数量会消耗大量计算资源,难以实现实时故障诊断。压缩感知理论的稀疏性假设符合高维振动信号的分布特点,所以压缩感知理论在处理轴承振动信号问题方面具有巨大优势。当轴承振动信号在一定的变换后具有近似稀疏性,压缩感知理论可以利用较少的采样值,通过压缩匹配追踪算法,重构采样数据,检测稀疏观测值中表征轴承故障特征的成分,直接实现故障诊断,为滚动轴承的实时状态监测与故障诊断提供了便利性。

总而言之,压缩感知理论可以为海量数据的存储、传输难题提供解决思路,并且在滚动轴承信号的欠采样、故障特征提取和故障识别分类等多方面提供技术支持,对于机械设备的在线状态监测有重要的价值[24]。

1.1 信号观测

图1中，给定原始高维信号x∈RN，该信号可在观测矩阵Φ∈RM×N的作用下映射到低维空间，得到长度为M的低维观测信号y∈RM。显然，观测矩阵的行维度M需要小于列维度N。

并且，这是一种线性映射，即：

y=Φx

（1）

当Φ是随机测量矩阵时，原始高维信号x与线性映射后的低维信号y具有如下关系：

（1-ε）‖x-y‖2≤‖Φ（x-y）‖2≤（1+ε）‖x-y‖2

（2）

式中：ε—常数且ε∈（0,1）。

式（2）说明：通过式（1）线性变换可使变换前后信号在欧几里得空间的距离有近似保存，即原始高维信号的有效信息在这种压缩变换中得到了有效保留，这为特征提取提供了理论依据。

1.2 信号的稀疏表示

从低维观测信号y中恢复原始信号x时，由于M小于N，式（1）构成了欠定方程组，该方程组具有无穷多组解，无法唯一地从观测值中获得原始信号。但是，当原始信号具有稀疏性，意味着x中存在大量的0元素，仅有少量的非0元素。此时，增加了从y中成功恢复x的可能性。

原始信号x一般不是稀疏信号，此时可将原始信号进行稀疏表示。

将x在正交基矩阵Ψ上展开，有：

（3）

式中：Ψ—稀疏字典矩阵，Ψ=[Ψ1,Ψ2,Ψ3,…,ΨN]，Ψ∈RN×N；θ—N个元素构成的稀疏系数向量，θ=[θ1,θ2,θ3,…,θN]∈RN。

式（3）也可表示成矩阵形式：

x=Ψθ

（4）

当θ是K稀疏时，即向量中有K个非零元素值并且K小于N，可将向量θ视为原信号x在字典矩阵Ψ上的稀疏表示系数。

结合式（1）与式（4），标注A=ΦΨ，得到压缩感知的矩阵形式：

y=Φx=ΦΨθ=Aθ

（5）

当Ψ是固定字典时，如DCT字典、小波字典等，这些固定字典的稀疏表示方式不能灵活地表示振动信号的复杂性，且不具有自适应性，影响测量重构精度。基于振动信号特征学习而来的字典，可以充分表征信号的故障特征，使得振动信号在该字典的稀疏表示方式下足够稀疏，需要的压缩测量值少，且更易获得高精度的重构信号。

字典学习方法如K-SVD算法，可以很好地对振动信号进行稀疏表示。

K-SVD算法的核心步骤包含3步：

（1）初始化字典。为了更好地稀疏表示信号，在轴承历史数据中选取k列作为初始字典；

（2）稀疏编码阶段。根据初始字典Ψ，利用贪婪算法得到x在字典Ψ上的稀疏系数矩阵θ，此步骤的重建算法是OMP算法，鉴于OMP算法重构效率低，该研究用SQSWOMP算法代替OMP算法，有助于实现实时故障诊断；

（3）固定θ，更新Ψ，当重构误差达到可接受范围时，停止更新。

K-SVD算法可以根据振动信号的特点，构造出具有自适应性的过完备字典。

1.3 信号重构

当信号x经过稀疏变换后，并且测量矩阵Φ与字典Ψ不相干，此时可通过匹配追踪算法成功恢复原始信号。重构问题由下式所示：

（6）

式中：T0—目标稀疏度值。

在匹配追踪算法中,SWOMP算法的优点是不需要将稀疏性作为先验条件,减少了对测量矩阵的要求,适用于滚动轴承信号的重构问题;但SWOMP算法的重构精度有待提升,这也是该研究着重解决的问题。

2 故障诊断方法及改进贪婪算法

2.1 基于改进SWOMP算法的故障诊断方法

根据压缩感知理论,笔者提出了基于改进SWOMP算法的实时滚动轴承故障诊断方法。该方法主要包括振动信号采集压缩、压缩后的信号传输与数据处理等3部分,整体的流程如图2所示。

图2中：实时信号采集系统用随机观测矩阵Φ对传感器采集到的原始高维振动信号进行了欠采样，得到测量值y。当托普利茨矩阵作为观测矩阵时，可以得到很好的重构效果，并且可以明显地加快运算速度，减少其存储空间[25]，故该研究中的随机观测矩阵采用托普利茨矩阵。

信号传输系统负责将低维观测值传输至远程监控中心，在监控中心完成数据处理。数据处理过程主要包括用改进的K-SVD算法训练n+1种历史振动信号，生成n+1种过完备字典，并用SQSWOMP算法重构低维观测信号，得到稀疏表示系数。根据稀疏系数进行数据分析，即可得到信号状态。

数据分析的具体过程如图3所示。

数据分析过程的原理在于不同的字典稀疏表示信号的能力不同。具有相同故障特征信息的字典可以很好地稀疏表示同种信号,得到的稀疏表示误差小,用其他属性信号训练得到的字典稀疏表示误差较大。这是由于学习字典具有自适应能力强、描述特征能力强的特点,所提取的字典原子与信号本身是线性关系,可以很好地模拟信号特征信息。

将实时信号通过若干种训练好的字典,稀疏表示误差最小的字典包含着与实时信号相同的故障特征信息,即可将实时信号判定为与该字典相同的状态。

基于SQSWOMP算法的滚动轴承故障诊断方法具体步骤如下:

（1）采集滚动轴承历史振动信号,设定有n+1种工况信号:正常工况、故障状态1、故障状态2、故障状态3、…、故障状态n;

（2）用SQSWOMP算法代替传统K-SVD算法稀疏编码阶段的贪婪算法,得到改进的K-SVD算法。结合n+1种轴承工况数据,训练得到n+1种字典,分别为Ψ0（正常工况信号训练得到的字典）、Ψi（故障状态（i=1,2,3,…,n）训练得到的字典）,将过完备字典作为先验知识;

（3）选用托普利茨矩阵作为随机观测矩阵,对实时采集系统采集到的信号x进行压缩采样,得到低维观测值y=Φx;

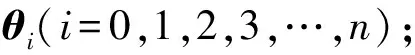
（7）

（6）根据式（7）可以得到n+1个表示误差，选取最小的表示误差对应的字典状态即判定为轴承故障状态，理论上最小的表示误差应接近0。例如，在上述n+1个表示误差中，若σ0=min{σ0,σ1,σ2,…,σn}，即判定轴承没有发生任何故障，处于正常状态；若σp=min{σ0,σ1,σ2,…,σn}，则判定轴承处于状态p。

2.2 改进SQSWOMP算法

解决轴承故障诊断问题时，常见的重建算法是贪婪算法。由于故障信号的稀疏度是未知的，像OMP、SP算法需要预估稀疏度，SWOMP的优势是不需要预知信号的稀疏度信息，很适合于处理未知故障信号的重构问题。

SWOMP算法的主要思想是采用内积准则从传感矩阵中挑出与残差信号较为匹配的原子集。其具体步骤如下：

（1）已知传感矩阵A=ΦΨM×N，观测向量y∈RM，设置迭代终止条件，门限阈值α，α∈（0,1）；

（2）初始残差ro=y，原子支撑集Λ0=Ø，A0=Ø，迭代次数t=0；

（3）求矩阵A与残差rt-1的内积绝对值u=abs[ATrt-1]，选取内积绝对值大于等于α*max（u）对应的原子序号，组成预选原子支撑集J0=find（u≥α*max（u））；

（4）合并预选集J0与原支撑集Λt-1，得到支撑集Λt=Λt-1∪J0，Λt记录每次迭代过程中选择的原子的列序号；合并At=At-1∪aj,j∈J0，At记录每次迭代过程中传感矩阵A中在原子支持集中包含的列。当At=At-1，则停止迭代；

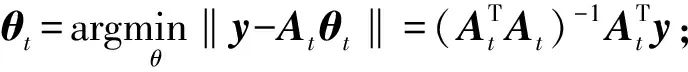
（6）更新残差rt=y-Atθt，当残差在一定范围内，停止迭代进入步骤8；

（7）t=t+1，当迭代次数超过允许范围内，停止迭代进入步骤（8），否则进入步骤（3）继续迭代；

由上述分析可知：门限阈值参数α决定SWOMP算法筛选的原子集，这导致SWOMP算法重建性能依赖于α。SWOMP算法不同于OMP算法，OMP算法在每次迭代更新字典原子的过程中要寻找最优解，而SWOMP算法则是选取部分原子，虽然其提升了重建速率，但导致算法的重建精度低。

基于SWOMP算法对门限阈值的选取敏感性较大与重建精度低等缺点，笔者提出SQSWOMP算法，具体的改进之处见下文。

2.2.1 改进SWOMP算法依赖门限阈值的问题

门限阈值α对重建精度有很大影响，在迭代过程中，使用固定阈值容易导致低估或高估的结果。针对SWOMP算法在每次迭代中都选择固定阈值参数的缺点，笔者提出了改进算法，基于S形函数具有初始阶段快速接近、最终阶段逐渐接近的特点，用S形函数值代替每次迭代中的固定阈值。这使得在迭代前阶段通过大步长快速接近理想的门限阈值，后阶段缓慢接近门限阈值，实现自适应地重构信号，提高了信号重构效率。

门限参数α∈（0,1），将5种经典的S形函数缩放至（0,1）之间。5种S形函数如图4所示。

图4中,5种函数均呈现先快后慢,最后趋于稳定的趋势。

f1为反正切函数：

f1=0.78arctan（3.5x）

（8）

f2为双曲正切函数：

（9）

f3是误差函数：

（10）

f4、f5是代数函数：

（11）

（12）

SQSWOMP算法的S形函数采用f3函数，具体原因将在实验部分进行讨论。

2.2.2 改进SWOMP算法原子支撑集选择问题

SWOMP算法在重建信号时，选取的是与原信号较为相关的若干个原子，而不是与原信号最相关的原子，这会导致不可靠的原子被选择，是影响重建精度的关键问题。针对该问题，SQSWOMP在SWOMP算法的一次弱选择原子的基础上，增加了回溯过程，进行原子的二次选择，删除不可靠的原子以获得最终的原子集。

二次选择原子的原则是：

（13）

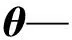
式（13）表明：在第二次选择原子的过程中，首先求得系数向量的每一项元素的绝对值，选取绝对值小于平均值的那些元素，其对应在Λt中的原子序列号Λtpos，即组成了Jdel。二次选择过程的目的是剔除原子支撑集中错误、贡献小的原子序列。

综上所述，改进的SQSWOMP算法的步骤如算法1所示。

算法1：SQSWOMP算法

输入:

传感矩阵A=ΦΨM×N

观测向量y∈RM

迭代次数S，默认为20

初始参数x0，x0∈（0,1）

步长b=0.1

初始化：

残差ro=y，Λ0=Ø，A0=Ø，t=0，x0=0.5

Whilet≤Sdo

1t=t+1

2u=abs[ATrt-1]

-----------------------------------------------------

-----------------------------------------------------

3α=f（x0），f（x）是S形函数

4J0=find（u≥α*max（u））

5x0=x0+b

6Λt=Λt-1∪J0

7At=At-1∪aj,j∈J0

10Λt=ΛtJdel

11At=AtAJdel

13rt=y-Atθt

14If‖rt‖≤1e-4:

Break

Endif

-----------------------------------------------------

-----------------------------------------------------

Endwhile

不同于SWOMP算法的迭代步骤，SQSWOMP算法不采用固定的门限参数α，在每次迭代过程中，通过S形函数值f（x0）自适应调整门限阈值，减少了迭代次数，在算法1的步骤4有所体现。

此外,在SWOMP算法原子支撑集选择过程的基础上,笔者增加了一次原子支撑集的删除过程,如果选中的原子对恢复信号的贡献小,则删除之前选择的错误原子,提高了重构效率与精度,在算法1的步骤9有所体现。

SQSWOMP算法流程图如图5所示。

3 仿真实验验证

滚动轴承振动信号是由：冲击成分、转频及其倍频等谐波成分和噪声组成的信号。因此，构造仿真信号数学模型为y（t）=h（t）+s（t）+n（t）。

其中，h（t）为冲击成分，s（t）为谐波成分，n（t）为高斯白噪声，具体如下：

（14）

式中：α—衰减系数，α=700；f0—故障频率，f0=120 Hz；T—故障周期，T=1/120 s；f1—固有频率，f1=4 000 Hz；f2—转频，f2=30 Hz；fs—采样频率，fs=16 000 Hz。

采样点数为4 000，观测值是1 024，采用托普利茨观测矩阵，添加的高斯白噪声SNR是10 dB。

仿真信号y（t）的时频域波形图如图6所示。

笔者用SQSWOMP、SWOMP、SP、OMP、SAMP算法分别对仿真信号进行了重构,并讨论了这5种算法的重构效果、重构精度和运算时间。

对于5种重构算法,重构信号的时域波形如图7所示。

图7是用5种重构算法重构仿真信号得到的时域波形图。为了展示波形细节,笔者取5 ms的波形进行观察,其中,实线代表原始信号波形图,虚线代表重构信号波形图,两条线的重合程度越高,代表重构效果越好。由此可以看出:SQSWOMP算法重构效果最好,两条线十分吻合;SP算法的重构效果仅次于SQSWOMP算法,优于OMP算法,SAMP算法存在一定的误差,SWOMP算法的重构效果最差,两条线的差距比较大。

对于5种重构算法,重构信号的频域波形如图8所示。

图8表明:SQSWOMP算法重构信号在频域也与原信号频域波形十分吻合,很好地凸显了载频30 Hz、故障频率120 Hz及其倍频;SP算法、OMP算法可以检测出载频、故障频率及其倍频,但是载频的振幅有一定程度的衰减,说明排除噪声的影响能力不如SQSWOMP算法;SAMP算法可以检测出载频、故障频率,但振幅也有所衰减,并且无法准确检测到故障频率的倍频;SWOMP算法的重构效果最差,载频振幅的衰减程度较大,并且无法检测到故障频率的倍频。

因此,SQSWOMP算法重构波形的效果最优。

5种重构算法重构信号的平均误差与运行时间,如表1所示。

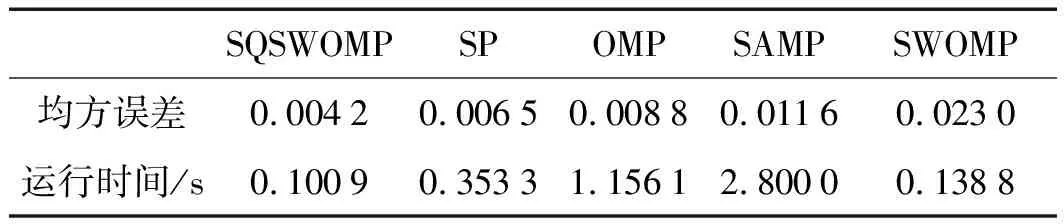
表1 不同算法重构信号的均方误差与运行时间

表1说明:SQSWOMP算法的重构精度和运算时间均优于SP、OMP、SAMP、SWOMP算法。

仿真信号实验结果表明:SQSWOMP算法可以解决稀疏度未知的振动信号的重构问题,在重构效果、精度和运算时间上均优于传统的重构算法。

4 实验验证

实验采用采样频率为12 kHz的美国凯斯西储大学6205-2RS JEK SKF深沟球轴承振动信号数据,以验证该文提出的故障诊断方法的有效性。轴承数据是一维振动信号,利用移动滑窗法,每512个数据点取一列,将一维信号分割成矩阵,得到训练集、测试集样本,训练集样本用于字典训练,测试集样本用来验证算法的重建效率和故障诊断成功率[26，27]。

对于远程监控中心而言,训练集是轴承历史数据,测试集为实时监测得到的数据。轴承故障可能发生在内圈、外圈或滚动体部位。因此,将训练集、测试样本均分为4类:正常工况、内圈故障、外圈故障、滚动体故障样本。训练集每种类型的样本包含3 000个信号,测试集每种包含800个信号,如表2所示。

表2 样本集

4.1 S形函数选取问题

笔者研究的第一个改进点就是用S形函数值自适应调整门限阈值参数值。笔者分别用5种典型的S形函数优化SWOMP算法,讨论它们对4种工况信号的重建能力。

重建精度用指标RSNR衡量,重构信号的RSNR定义如下:

（15）

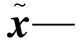
RSNR越大,表示重建效果越好。

笔者设观测值为110,迭代次数为20次,初始化参数x0取0.5,分别用5种优化后的算法对4类测试信号做500次实验,取其平均的RSNR,结果如表3所示。

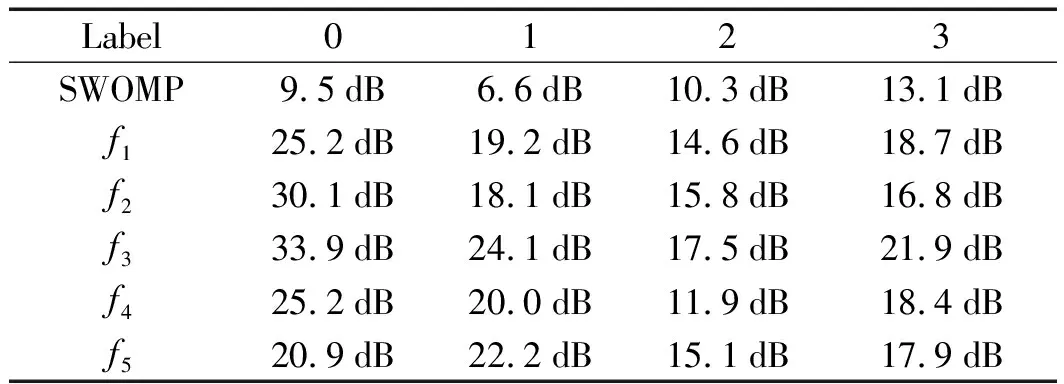
表3 5种S形函数优化后的算法的PSNR对比

由表3可以看出:5种S形函数优化的SWOMP算法对4种测试信号的重建效果相差不大,但比传统的SWOMP算法精度要高,并且f3函数优化的SWOMP算法精度最高,故SQSWOMP算法中的S形函数采用f3函数。

4.2 SQSWOMP算法重构四种工况信号

为了验证SQSWOMP算法重构信号的能力,笔者用SQSWOMP算法重构原始一维的4种工况信号,采样点数为4 096,测量数目为1 024,测量矩阵采用托普利茨矩阵,结果如图9所示。

图9中,重构信号与原信号的波形十分吻合,用SQSWOMP算法重构信号,时域与频域恢复效果具有良好的鲁棒性,可提取出轴承信号的有效成分。

4.3 基于SQSWOMP算法的故障诊断框架可行性分析

在验证了SQSWOMP算法的性能后,笔者提出基于SQSWOMP算法的实时轴承故障诊断方法,用SQSWOMP算法代替传统的K-SVD算法稀疏编码阶段的重构算法,如之前图2所示。

该方法的重点在于轴承故障字典的建立、快速准确地实现重构目的以及数据分析过程。

为了更好地凸显轴承故障特征信息,用改进的K-SVD算法训练得到能体现出轴承故障信息的学习字典。

K-SVD算法的参数设置如下:原子数量设为1 024,迭代次数为20,观测矩阵采用托普利茨矩阵,观测值选取110;利用改进的K-SVD字典学习算法,分别训练这4种训练信号构成的过完备字典,得到Dnormal、Dinner、Dout、Droll。

为了测试这4种字典的稀疏表现性能,笔者分别在4种字典上,依次将4种工况的测试样本进行稀疏表示,用余弦相似度来衡量样本与重构后的样本的相似程度,余弦相似度衡量了两个向量的夹角（在[-1,1]中取值,值越靠近1,表明原样本与重构后的样本的相似程度更高,稀疏表示效果更好）,结果如图10所示。

图10中，横坐标是800个测试样本序列，纵坐标是重构信号与原信号的余弦相似度。

图10（a）表明：将正常工况信号在4种字典上稀疏表示，正常字典Dnormal的稀疏表示重构误差最小；

图10（b）表明：将内圈测试信号在4种字典上稀疏表示，内圈字典Dinner的稀疏表示重构误差最小；

图10（c）表明：将外圈测试信号在4种字典上稀疏表示，外圈字典Dout的稀疏表示重构误差最小；

图10（d）表明：将滚动体测试信号在4种字典上稀疏表示，滚动体字典Droll的稀疏表示重构误差最小，并且重构效果远远优于其他3种字典的稀疏表示效果。

图10验证了振动信号在由其同种特征信号训练得到的字典上稀疏表示性能更好,在异种特征信号组成的字典上稀疏表示性能较差,意味着可以通过经过训练的故障字典去稀疏表示实时信号,使得稀疏表示误差最小的字典和实时信号的故障特征信息最为接近。

该结果验证了笔者提出的故障诊断方法的可行性。

4.4 观测值对故障诊断性能的影响

为了验证用SQSWOMP算法取代传统K-SVD稀疏编码阶段的OMP算法的有效性,以及研究观测数目M与故障诊断性能的关系,笔者将4组测试信号通过该方法进行分类,并增加4组对照实验（4组对照实验的不同在于K-SVD稀疏编码阶段的重构算法,以及稀疏表示阶段的重构算法分别用SWOMP、OMP、SP、SAMP算法）,结果如图11所示。

图11中,横坐标代表观测值M,纵坐标是故障诊断成功率。

由图11可以看出:随着压缩观测量M的增加,4种轴承信号的故障识别率呈现逐渐提高的趋势,观测值在达到一定值时,识别率将趋于稳定;

图11（a）是该方法在正常工况测试信号上的表现,基于SQSWOMP算法的故障诊断方法在M到达70时,达到接近百分之百的故障诊断成功率,并且优于其他重构算法性能;

图11（b）体现了该方法在内圈工况信号上的表现，M在70左右可以达到接近百分之百的故障诊断成功率；

图11（c）表明了该方法在外圈故障信号上的分类性能，在观测值70左右，可达到百分之百的识别率；

图11（d）为该方法在滚动体故障信号上的分类性能，在M为110时，可以达到接近百分之百的故障分类成功率。

ZHANG Xin-peng等人[16]1258-1259的研究表明,用传统K-SVD算法训练字典进行故障诊断时,当M为80时,正常、内圈、外圈、滚动体工况信号的故障识别率分别是97.88%、81%、85.25%、80.25%。

用SQSWOP算法代替传统K-SVD算法稀疏编码的重构算法,在相同的观测值下,可以将故障诊断成功率分别提升2.17%、23.46%、17.30%、18.38%。

可见,改进的K-SVD算法可以用更少的观测值得到较高的诊断成功率,训练得到的字典可以很好地模仿轴承故障特征信息,有效实现滚动轴承实时故障诊断。

4.5 与其他方法比较

为了进一步证明方法的有效性，笔者将该方法与其他轴承故障诊断模型进行对比。其中，SVM的核函数采用径向基核函数（Radial Basic Function, RBF），初始值c1=0.8，c2=0.8；BP神经网络的输入节点为4，隐含层节点为25，输出节点为3；KNN算法k为4，采用k-d树算法。

笔者对4种工况下的3 200个样本随机进行测试,平均故障诊断成功率如图12所示。

由图12可以发现:基于KNN、BP、SVM故障诊断方法准确率有待提升,原因是轴承振动信号中含有大量干扰噪声,并且处于故障状态的信号本身就具有非平稳、非线性等特点,导致这些分类模型无法直接应用于提取非线性含噪信号,需要进行参数寻优或是在提取故障信息后再输入分类模型;

该方法的诊断准确率很高,在观测值设置合理的情况下,可达到接近百分之百的平均诊断准确率。这是由于构造的过完备字典是根据训练信号学习而来,具有自适应性,可以充分体现故障特征信息,并且改进贪婪算法,使得其在保证高效率的情况下,提高了重建精度;

另外,该方法可以不需要存储传输原始高维信号,当重建精度一定时,可以使用更少的观测值高精度地压缩信号,只需要存储、传输压缩后的低维信号,用低维信号进行故障诊断,大大减轻了数据存储与传输方面的负担,为实时故障诊断提供可能。

5 结束语

采用香农定理的传统滚动轴承故障诊断方法,会在持续的状态监测过程中产生海量数据,原始数据往往含有较多与故障无关的信息,使得振动信号的传输、存储有很大的压力,并且造成硬件资源的浪费。为此,笔者提出了一种基于改进SWOMP算法的轴承故障诊断方法,用改进的K-SVD算法提取非线性振动信号的特征,然后生成故障特征字典,利用稀疏表示误差最小化原则,对实时轴承信号进行了预测分类,在减轻存储、传输压力,同时实现了对滚动轴承的故障诊断。

笔者的主要贡献有以下几点:

（1）重构算法方面的改进。针对SWOMP算法对门限阈值参数依赖性大和重建精度低等问题,在SWOMP算法中引入S形函数并增加了原子支撑集的二次选择过程,进行了改进,提高了重建算法的精度与效率,使得重构信号更加稀疏并且迭代更快;当重建精度一定时,可以用更少的观测值实现重构信号。实验结果表明,SQSWOMP算法有效地解决了SWOMP算法重构精度低的问题,并且提高了信号重建速率,在重构效率、精度方面均优于常见的贪婪算法;

（2）故障诊断准确率的提升。将改进的SQSWOMP算法应用于K-SVD算法中,取代K-SVD算法稀疏编码阶段的重构算法,验证了改进的K-SVD算法的有效性,应用到轴承故障诊断问题上,可以准确地提取故障特征。在相同的观测值下,可以将4种工况的故障诊断成功率分别提升2.17%、23.46%、17.30%、18.38%,解决了内圈、外圈、滚动体工况故障诊断准确率低的问题,并且由于字典是由振动信号训练而来,所以故障诊断方法具有自适应性,可以解决不同振动信号的故障诊断问题;

与其他方法相比,该方法在4种工况信号的故障诊断准确率均高于其他机器学习算法。该方法只需利用压缩后的数据直接进行故障诊断,解决了长期状态监测海量数据存储与传输方面的问题,并为实时故障诊断提供了便利。

该研究的研究对象是滚动轴承的单一类型故障。在后续的工作中,笔者将研究该方法在多故障融合情况下的适用性。此外,由于数据样本有限,笔者未获取数据库以外的轴承振动信号,在之后的工作中,笔者将获取更多的数据样本,以验证该方法的有效性。