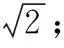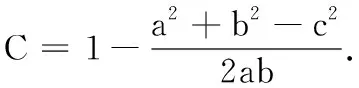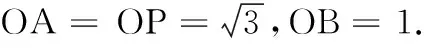高三数学综合测试
一、单项选择题(本大题共8小题,每小题5分,计40分)
1.已知集合P,Q均为R的子集,且(RQ)∪P=R,则( )
(A)P∩Q=R(B)P⊆Q
(C)Q⊆P(D)P∪Q=R

4.《张邱建算经》曾有类似记载:“今有女子善织布,逐日织布同数递增(即每天增加的数量相同)".若该女子第一天织布两尺,前二十日共织布六十尺,则该女子第二十日织布( )
(A)三尺 (B)四尺 (C)五尺 (D)六尺

(A)1 (B)2 (C)-1 (D)±1
6.已知直线y=x-2与抛物线y2=4x交于A,B两点,P为AB的中点,O为坐标原点,则|OP|2-|PA|2=( )
(A)2 (B)-2 (C)4 (D)-4
7.已知函数
若关于x的方程f2(x)-(k+1)xf(x)+kx2=0有且只有三个不同的实数解,则正实数k的取值范围为( )
(C)(0,1)∪(1,2) (D)(2,+∞)
8.连续向上抛一枚硬币五次,设事件“没有连续两次正面向上”的概率为P1,设事件“没有连续三次正面向上”的概率为P2,则下列结论正确的是( )
(A)P1+P2=1 (B)P2<2P1
(C)P2=2P1(D)P2>2P1
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

(C)f(x)的最小正周期为π
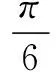
10.已知a>0,b>0,a+2b=1,则下列结论正确的是( )
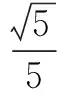
(C)log2a+log2b的最小值为-3
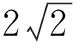
11.已知O为坐标原点,圆Ω:(x-cosθ)2+(y-sinθ)2=1,则下列结论正确的是( )
(A)圆Ω恒过原点O
(B)圆Ω与圆x2+y2=4内切
(D)直线xcosα+ysinα=0与圆Ω相离
12.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,G,H分别是所在棱上的动点,且满足DH+BG=AE+CF=1,则以下四个结论正确的是( )
(A)E,G,F,H四点一定共面
(B)若四边形EGFH为矩形,则DH=CF
(C)若四边形EGFH为菱形,则E,F一定为所在棱的中点

三、填空题(本大题共4小题,每小题5分,计20分)
13.命题“∀n∈N,n2-1∈Q”的否定为______.
14.在平面直角坐标系xOy中,圆M交x轴于A(-2,0),C(4,0),交y轴于B,D,四边形ABCD的面积为18,则OM=______.

四、解答题(本大题共6小题,计70分..解答应写出必要的文字说明、证明过程或演算步骤)
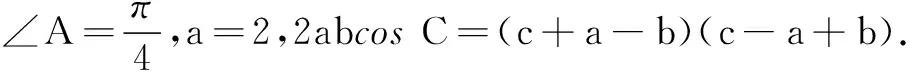
(1)求C;
(2)求∆ABC的面积.
18.(本小题满分12分)已知数列{an} 前n项积为Tn,且an+Tn=1(n∈N*).
19.(本小题满分12分)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,∠BAD=∠BPD=60°,PB=PD=2.
(1)证明:平面PAC⊥平面ABCD;
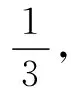
20.(本小题满分12分)某学校共有3 000名学生,其中男生1 800人.为了解该校学生在校的月消费情况,采取分层抽样的方式,抽取100名学生进行调查,先统计他们某月的消费金额,然后按男女性别分成两组,再分别将两组学生的月消费金额分成5组:[300,400),[400,500),[500,600),[600,700),[700,800)分别加以统计,得到如图所示的频率分布直方图.
(1)样本中将月消费金额不低于600元的学生称为“高消费群”.请你根据已知条件完成下列2×2列联表,并判断是否有97.5%的把握认为该校学生属于“高消费群”与“性别”有关?

属于“高消费群”不属于“高消费群”合计 男 女 合计
(参考公式:

P(K2≥k)0.150.100.050.0250.0100.0050.001 k2.0722.7063.8415.0246.6357.87910.828
(2)以样本估计总体,以调查所得到的频率视为概率,现从该学校中每次随机抽取1名学生,共抽取4次,且每次抽取的结果是相互独立的,记被抽取的4名学生中“高消费群”的人数为X,求X的期望E(X)和方差D(X).
21.(本小题满分12分)已知圆O:x2+y2=4 与x轴交于点A(-2,0),过圆上一动点M作x轴的垂线,垂足为H,设MH的中点为N,记N的轨迹为曲线C.
(1)求曲线C的方程;
(1)若a (2)若a>e,求证:函数f(x)有且仅有1个零点. 参考答案 一、单项选择题 1.C;2.A;3.A;4.B;5.D; 6.D;7.B;8.B. 二、多项选择题 9.AC;10.AD;11.ABC;12.AD. 三、填空题 四、解答题 19.(1)设AC∩BD=O,连结PO,在菱形ABCDK中,O为BD中点,且AC⊥BD. 因为PB=PD,所以BD⊥PO.又因为PO∩AC=O,PO,AC⊂平面PAC,所以BD⊥平面PAC. 因为BD⊂平面ABCD,所以平面PAC⊥平面ABCD. 20.(1)依据频率分布直方图得 属于“高消费群”不属于“高消费群”合计 男154560 女202040 合计3565100 显然其判别式Δ>0. 综上,k1=4k2. 综上,当a>e时,f(x)有且仅有1个零点.