求解一道复数竞赛试题的第三视角
2022-10-26 09:42:28王银祥
高中数学教与学 2022年17期
王银祥
(江苏省沭阳县建陵高级中学,223699)
试题已知复数z满足|z|=1,则|z3+3z+2i|的最大值为( )

解注意到当z=-i时,z3+3z+2i=0,从而z3+3z+2i可因式分解为z3+3z+2i=(z+i)2(z-2i).于是有|z3+3z+2i|=|z+i|2|z-2i|.联想到复数的几何意义,问题转化为:如图1,已知点A(0,-1),B(0,2),点P为圆O:x2+y2=1上一动点, 求乘积|PA|2· |PB|的最大值.
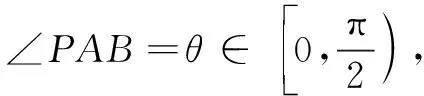
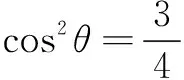
故选B.
评注通过观察发现目标式可以因式分解,这是解决本问题的关键.此后先利用复数模的运算性质、几何意义将问题转化为距离的乘积,再通过设辅助角为变量,运用余弦定理转化为三角函数模型.这种方法区别于文[1]所示的两种求解方法,最后的函数模型可以运用三元基本不等式求出最值,从而解决问题.
猜你喜欢
小学生学习指导(中年级)(2021年3期)2021-04-06 09:12:08
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
数学年刊A辑(中文版)(2018年1期)2019-01-08 01:58:22
智富时代(2017年4期)2017-04-27 02:13:48
数学学习与研究(2015年15期)2015-05-30 01:17:26
数学年刊A辑(中文版)(2014年2期)2014-10-30 01:40:54
数学教学通讯·初中版(2014年12期)2014-04-29 00:44:03
化学分析计量(2014年6期)2014-04-04 15:34:48

