应用柯西不等式的几个技巧

肖 芳

(山东省枣庄市第一中学)

当且仅当a1＝a2＝…＝an＝0或bi＝kai(k为常数)时,等号成立,这就是柯西不等式的一般形式.在解题中,关于柯西不等式的运用并非“直截了当”,往往需要运用一些方法与技巧,下面一起来看个究竟.

1 巧拆常数

柯西不等式的右侧是两个因式的乘积形式,于是我们可以将所求等式乘1,然后将1根据实际拆分成几个分数的和.

例1已知实数a,b,c,d满足a＋b＋c＋d＝3,a2＋2b2＋3c2＋6d2＝5,试求a的最值.

点评巧拆常数必须从实际出发,本题借助柯西不等式将等式转化为关于a的不等式,在这个过程中,柯西不等式发挥了化等式为不等式的作用.

2 重新排序

柯西不等式有着严格的次序特征,有些不等式问题需先调整有关项的位置,才能直接利用柯西不等式“对号入座”.

例2a,b为非负数,a＋b＝1,x1,x2∈R*,求证:(ax1＋bx2)(bx1＋ax2)≥x1x2.

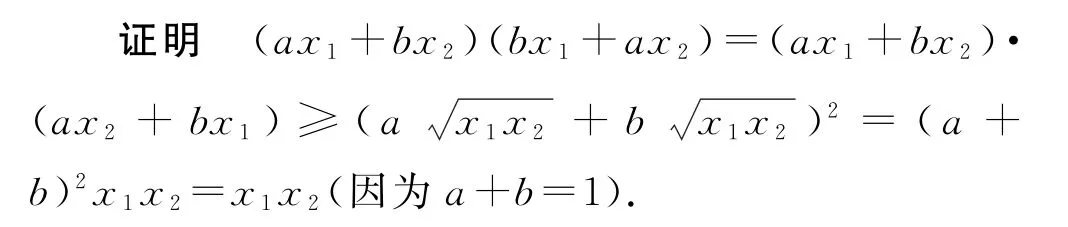
点评本题证明过程十分简明,体现了数学的简约之美,这源于柯西不等式的灵活应用.本题也可用作差法来证明,但过程比较烦琐.

3 改变结构

为充分利用柯西不等式,并感受它给解题带来的便捷,需对某些表达式对照柯西不等式进行“结构改造”,为柯西不等式的应用铺平道路.

点评求无理函数的值域是数学中的一个难点,尤其是含双根号的无理函数.而本题通过改变原函数的结构,灵活应用柯西不等式进行处理.

4 适当添项

对于某些不等式的证明问题,看似不具备柯西不等式的特征,但可以通过适当添项加以改造,再利用柯西不等式,从而使证明过程一气呵成.

例4a,b,c∈R*,求证:

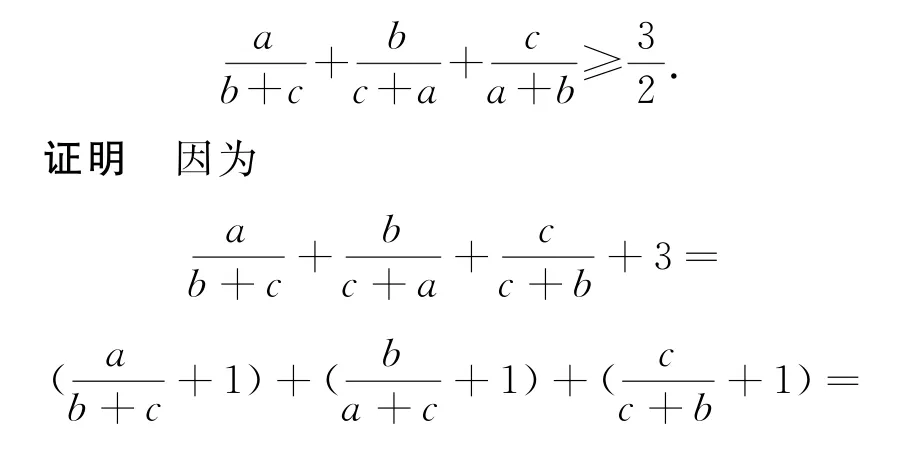
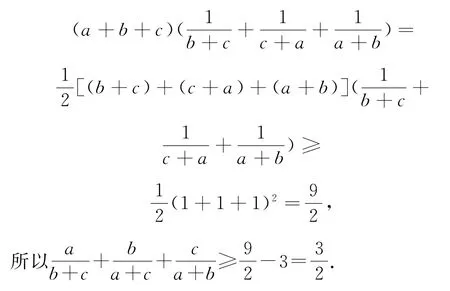
点评本题的证明过程体现了数学解题中的创新思维.适当添项,其实是一种构造思想.

5 利用等号成立的条件

关于柯西不等式的应用,不仅应关注其本身,也应关注其等号成立的条件,有时问题的解决恰恰是利用了这个条件.

点评本题之所以想到采用柯西不等式,原因在于已知等式的左侧具有柯西不等式的形式,而且在应用过程中正好把a,b消去,将不等式变成等式,只需关注等号成立的条件.这体现了柯西不等式的应用具有很大的灵活性.

6 引进待定参数

在解决某些特殊问题时,为了运用柯西不等式,我们往往会引进一些待定参数,它的值由题设或不等式等号成立的充要条件来确定.

点评本题具有一定的难度,难点之一是对所求不等式进行等价变形,难点之二是通过引进参数,将欲求的表达式变形,进而利用柯西不等式和等号成立的条件,求出参数的取值范围,从而求出欲求表达式的范围.

从以上6个例题不难看出,柯西不等式虽然用途十分广泛,但它的应用具有很大的灵活性.只有从问题实际出发,并对所求表达式适当变形,才可与柯西不等式“无缝对接”,同时应关注等号成立的条件,因为这也许是恒等式证明的一条途径.

(完)