不等式章节小测

麦 庆

(广东信宜砺儒中学)

(本试卷共22小题,满分150分,考试用时120分钟)

一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.)

1.若a,b满足a＞b,则下列不等式成立的是( ).

A.a＋b＜abB.a2＞b2C.a3＞b3D.

2.下列不等式恒成立的是( ).

A.a2＋b2≤2abB.a2＋b2≥－2ab

C.a＋b≥－D.a＋b≤

3.下列函数最小值为6的是( ).

4.关于x的不等式ax2－|x|＋2a≥0的解集是(－∞,＋∞),则实数a的取值范围为( ).

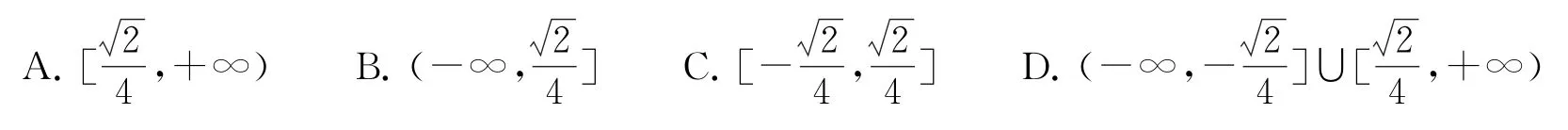
5.已知0＜x＜2,则y＝的最大值为( ).

A.2 B.4 C.5 D.6

6.若x＞0,则函数y＝2＋3x＋的最小值为( ).

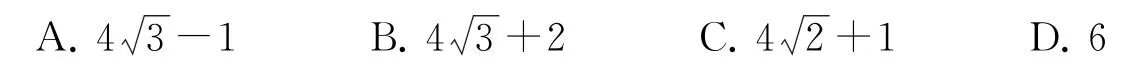
7.已知f(x)＝ex,若a＞0,b＞0,且f(a)f(2b)＝e2,则的最小值为( ).

8.设O为坐标原点,直线x＝a与双曲线＝1(a＞0,b＞0)的两条渐近线分别交于D,E两点,若△ODE的面积为8,则C的焦距的最小值为( ).

A.4 B.8 C.16 D.32

二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得2分.)

9.已知a,b,m均为正实数,则成立的充要条件是( ).

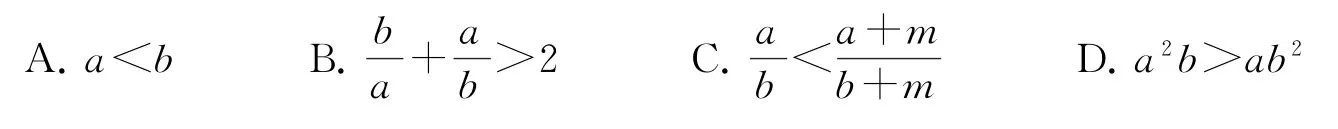
10.不等式ax2＋bx＋c≥0的解集是{x|－1≤x≤2},则下列结论正确的是( ).

A.a＋b＝0 B.a＋b＋c＞0 C.c＞0 D.b＜0

11.已知正数a,b满足a2＋b2＝2a＋2b,若a＋b∈Z,则a＋b的值可以是( ).

A.2 B.3 C.4 D.5

12.设a＞0,b＞0,则下列不等式恒成立的是( ).

A.a2＋1＞aB.a2＋9＞6a

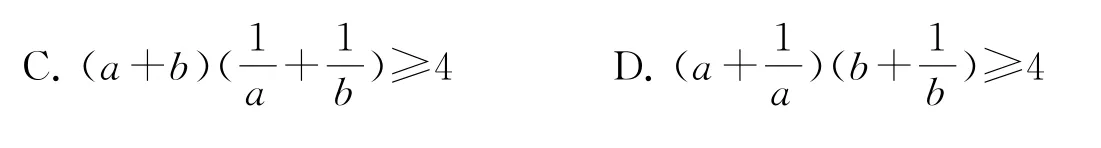
三、填空题(本题共4小题,每小题5分,共20分.)

13.(1)“x1＞0且x2＞0”是“x1＋x2＞0且x1x2＞0”的_________条件;

(2)“x1＞2且x2＞2”是“x1＋x2＞4且x1x2＞4”的_________条件.

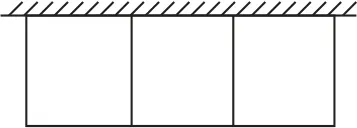
14.有一批材料可以建成长为200m 的围墙,若用此材料在一边靠墙的地方围成一块矩形的地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的整个矩形场地的最大面积是________(围墙的厚度不计).

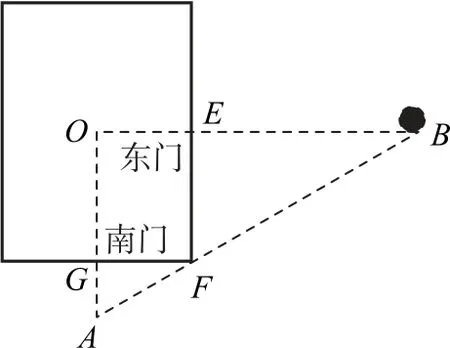
15.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木?”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门x里见到树,则x＝.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为(注:1里＝300步)_______里.

16.二次函数y＝ax2＋bx＋c(a≠0)的对称轴为y轴,经过(0,0),(1,1)两点,且当－1≤x≤1,－2≤m≤2时,y≤t2－2mt＋1恒成立,则实数t的取值范围是_________.

四、解答题(本题共6小题共70分.解答时应写出文字说明、证明过程或演算步骤.)

17.(10分)某工厂拟建一座底为矩形且面积为200m2的三级污水处理池(平面图如图所示),如果池四周的围墙建造单价为每米400元,中间两道隔墙单价为每米248元,池底建造单价为每平方米80元? 请你设计:污水处理池的长和宽为多少米时,总造价最低,并求出总造价.

18.(12分)已知正数a,b满足.

(1)求a＋b的最小值;

19.(12分)已知关于x的不等式2kx2＋kx－＜0,k≠0.

(1)若k＝,求不等式的解集;

(2)若不等式的解集为R,求k的取值范围.

20.(12分)(1)已知x＞3,求的最小值;

(2)已知x,y是正实数,且x＋y＝1,求的最小值.

21.(12分)(1)设b＞a＞0,m＞0,证明

(2)设x＞0,y＞0,z＞0,证明:

22.(12分)已知关于x的不等式x2－x＋a－a2≤0.

(1)当a＝2时,求不等式的解集;

(2)当a为常数时,求不等式的解集.