堆石坝密度的附加质量法测点振动影响范围研究

李晓磊，裴少英

(黄河勘测规划设计研究院有限公司，河南 郑州 450003)

1 概述

堆石坝压实质量的好坏直接影响坝体的沉降变形和稳定性。碾压质量检测的常用方法为灌水法，该方法受限于挖坑检测的方式，存在测量区域小、成本高、效率低等不足，且会对坝体造成一定程度的破坏。为寻求一种快捷、准确、无损的堆石土密度测量方法，1995年，黄河小浪底堆石坝施工过程中把“附加质量法”列入了大坝施工科研项目。“附加质量法”是以单自由度振动体系(质量—弹簧体系)为物理模型，以附加质量为手段，通过测量堆石土介质的动力参数(刚度、参振质量、自振频率)而测量堆石土密度的一种方法。该技术已在乌江洪家渡、长江水布垭、大渡河瀑布沟、田湾河仁宗海、河南燕山水库、澜沧江糯扎渡、昆明新机场等堆石坝、堆石土地基工程中得到不断测试和应用，测试技术水平和精度达到了较高水平[3- 8]。

上述文献成果可以看出，根据工作经验类方式估算振动影响深度是可行的，但在实践中堆石体的激振影响深度还有进一步研究的必要[9- 23]。通过上述文献启发以及多年实践，按照截头圆球体来推到起体积公式是可行的，因此本文做出一些尝试，并通过以往数据来验证推导出公式的合理性。

2 截头圆球体的体积理论公式推导

根据振动影响有效范围为一截头圆球体的结论，其体积公式理论推导思路为：“质—弹”体系中的质量m0相当于有质弹簧体系中弹簧质量m的1/3，将附加质量法测到的质量m0换算成介质振动的实际质量m，m=3m0，并将m除以相应的密度ρ换算成相应的体积V；再利用截头圆球体体积公式反求体积为V的球体半径r，得出测点振动影响半径，如图1所示。

圆球体体积公式

(1)

圆球冠体积公式

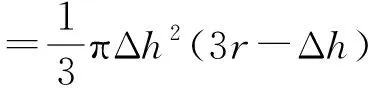
(2)

截头圆球体体积公式

V=V球-V冠

(3)

设承压板半径为r0,m;球体半径为r,m;球冠高为Δh,m;则可以推出Δh：

表1 代表性文献研究成果

(4)

(5)

(6)

将(1)、(2)、(4)式代入(3)式即得振动体积V与承压半径r0、振动有效影响半径r的关系，如(5)式，根据(5)式已知V、r0即可求得振动的影响半径r。

(7)

图1 截头圆球体示意图

3 模拟计算

为验证理论推导结果，基于澜沧江糯扎渡、四川田湾河仁宗海、大渡河瀑布沟堆石坝堆石土料的部分附加质量法及坑测法实测数据，进行测点影响范围(影响半径和影响深度)的理论模拟计算。

表2 测点振动有效影响半径(r)及深度(h)计算表

3.1 振动影响范围的计算

糯扎渡工程33组堆石土实例资料，仁宗海工程32组堆石土料实测资料，瀑布沟工程16组实测资料中振动有效影响范围的计算结果见表2。可以看出：

表2中，r0、r分别为承压板半径、振动有效影响半径；m0、m、ρω、V分别为相应质弹体系振动模型的堆石土参振质量、有质量弹簧体系振动模型的堆石土实际参振质量(m=3m0)、堆石土湿密度以及相应m的体积(V=m/ρω)；h、Δh为振动有效影响深度以及承压板以上球冠的虚拟高度。

3.2 有效影响边界的应力比计算

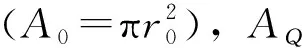
(8)

根据(8)式可计算边界球面处的应力比Pr/P0，结果见表3。

表3 计算结果

4 结语

堆石体密度的附加质量法测点振动影响范围与地基振动影响类似，在其基础上通过推导得出理论公式，进而得到测点影响范围、深度与承压板、应力之间的关系。结果如下：

(1)推测测点振动的有效影响范围为一截头圆球体，经过理论公式推导和数据正演，该推测与实际相符合。

(2)基于截头圆球体模型进行测点振动影响范围的理论推导，得到可用于模拟计算振动影响半径的理论公式。

(3)得出承压板与振动影响深度之间的关系。有效振动范围边界处的应力与承压板底部的应力比约为0.05；水平向有效振动影响半径为承压板半径的2.3倍有效；振动影响深度为承压板半径的4.4倍。

本文的研究成果有助于改进现有的附加质量法现场测试方法及步骤，提高了附加质量法测试的准确性。理论公式尚需进一步实验模型验证，我们将在后续的研究中给出。