基于PRGM-Markov链的管道腐蚀动态预测技术
古江涛 王增涛 王世伟 蒋银举 王平 张红
1中国石油天然气股份有限公司华北油田分公司
2中国石油华北油田公司储气库管理处
3中国石油华北油田天成公司
4中国石油华北油田公司第五采油厂
5中国石油华北油田公司第三采油厂
在内部腐蚀介质和外部环境的影响下,油气管道极易发生腐蚀穿孔事故,且我国大部分管道服役时间已接近设计寿命,进入事故多发期[1-2]。因此,对管道特殊部位的数据进行采集,研究腐蚀发展规律,并对管道剩余寿命进行预测,对预防管道泄漏和制定合理的检验维护策略具有重要意义。
目前,国内外学者对管道剩余寿命的预测主要采用神经网络[3]、概率统计[4-5]和灰色模型等,其中神经网络和概率统计均需大量数据样本,通过建立影响因素与腐蚀深度之间的关系,对管道寿命进行预测。在缺少数据样本的条件下,常采用灰色理论中的GM(1,1)模型对腐蚀发展趋势进行预测,但在实际应用中,GM(1,1)的预测结果会随着数据波动产生较大误差,针对这一问题,大量学者对其进行改进。骆正山等采用RBF模型对GM(1,1)模型的残差进行了修正[6];俞树荣等通过对原始数据平移增加序列的准光滑性和准指数性[7];贾宝惠等提出不等时间距GM(1,1)模型,并对权重参数和背景值进行了优化[8];张新生等建立了尾段残差修正的GM(1,1)模型,平均相对误差3.79%[9]。以上研究对GM(1,1)模型的发展和改进具有推动作用,但仍存在改进方式单一、预测结果受原始数据影响较大等问题,且单一的灰色模型未考虑系统内的随机性,在中长期预测方面效果较差。Markov 链适用于数据波动较大的中长期预测[10],GM(1,1)预测模型的残差属于随机波动序列,满足Markov 链可处理随机过程状态转移的特点。基于此,构建无偏灰色GM(1,1)模型,同时对数据信息和背景权值进行优化,依据相对误差范围引入Markov 链对预测结果进行残差修正,并结合实例对模型的合理性和准确性进行验证。
1 传统GM(1,1)模型
首先,根据现场腐蚀深度检测结果构建原始数据序列:

式中:n为检测次数,x(0)(n)即为第n次检测得到的腐蚀深度。
为减弱原始序列随机性对预测结果的影响,对原始序列进行一阶累加后得到AGO序列:
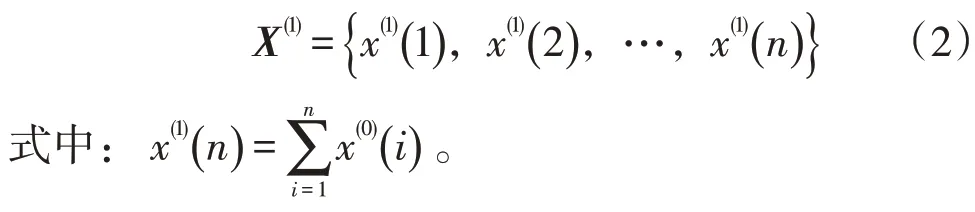
根据AGO序列构建背景值序列:

式中:λ为背景权值。
根据背景值序列对白化方程离散化,将微分转化为差分,从而得到GM(1,1)模型均值形式:

式中:a、b分别为发展系数和灰色作用量,可通过最小二乘法计算得到。
最终确定GM(1,1)模型的预测公式为:

2 优化GM(1,1)模型
传统灰色模型使用的不是原始数据序列,而是生成的数据序列,其核心体系是对原始数据做累加生成(或其他方法生成)得到近似准指数规律后再进行建模的方法,它可解决历史数据少、序列可靠性和完整性低的问题,并且易于检验,无需考虑分布规律和变化趋势的影响。但在使用的过程中存在以下问题:当原始数据增长速度过快时,传统模型在指数序列建模中存在固有偏差,导致预测结果出现大幅波动;理论上传统模型可预测未来任意时刻的数据,但对于系统而言,随着时间延长,随机干扰因素不断加入系统,使模型的预测精度大幅降低,传统模型无法实时反映系统的变化情况;背景权值λ通常取0.5,即用梯形面积代替了积分区域面积,当处理某些剧烈变化的数据时,传统背景值的构造方法会带来较大误差,且λ直接影响发展系数a的计算精度,导致最终预测结果受到较大影响。针对以上3个缺陷,分别从无偏优化、等维信息更新和背景权值优化等三个方面对传统GM(1,1)模型进行改进。
2.1 无偏优化
为消除灰色偏差,对GM(1,1)进行无偏优化,优化后无需对预测值进行累减还原。最终,将公式(6)改为无偏优化GM(1,1)模型,公式为:

式中:c、A均为无偏灰色模型中待定参数。
2.2 等维信息更新
新的腐蚀数据更能体现腐蚀状态的变化,即数据应具有时效性和动态性。在保持原始序列不变的条件下,通过等维信息更新模型,不断更新预测数据并删除旧的数据,使用现有序列预测下一时刻的腐蚀深度;然后在原始序列的基础上去掉第一个数据,并加入最新的预测结果构成新的等维序列;依次类推实现对数据的动态更新。在此,将无偏优化等维信息GM(1,1)预测结果,记为RGM(1,1)模型。
2.3 背景权值优化
通过动态调整各区间λ值,对每一步的λ值进行寻优,最大程度降低因背景值序列造成的误差。粒子群(PSO算法)在处理非线性、多维度的复杂问题上具有一定优势,首先将n维数据输入模型,根据无偏灰色模型计算预测值;设定粒子的位置和速度,根据定义的适应度函数计算各粒子的适应度值,根据适应度值更新粒子的局部最优解和全局最优解,并更新粒子的位置和速度向量,反复迭代后得到最优λ,由此得到第一个预测结果;将预测结果代入等维信息更新模型,去除陈旧数据,将得到的新序列重复上述步骤后完成第二个预测结果,依次类推,直到完成所有值的预测。在此,将经PSO算法优化的RGM(1,1)预测结果记为RPGM(1,1)模型,模型的预测流程如图1所示。

图1 RPGM(1,1)模型预测流程Fig.1 RPGM(1,1)model prediction process
3 基于RPGM-Markov 链的腐蚀动态预测模型
当腐蚀深度实际值与预测值存在较大误差时,可采用Markov 链对预测结果中的波动性误差进行修正。Markov链具备无后效性,即预测对象的未来状态只与当前状态有关,与之前状态无关,正好可以弥补灰色模型对于中长期预测较差的缺点。在此,利用Markov 链修正GM(1,1)模型的预测值,形成基于RPGM-Markov 链的腐蚀动态预测模型,步骤如下:
首先,根据RPGM(1,1)模型得到腐蚀深度预测值,计算残差值e(k)和相对误差Q:
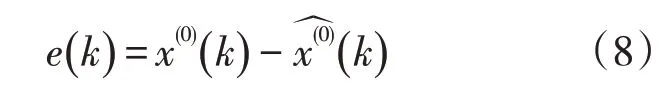

其次,根据相对误差序列的分布状态划分为i个Markov 状态区间,第h个状态区间即为对应状态区间的范围为根据相对误差序列与状态区间的关系,确定一步状态转移概率矩阵P。
最后,假设残差系统的初始状态为E0,经过数次一步转移后比较各状态的概率大小,并根据最大概率原则确定该时刻的预测状态,从而对腐蚀深度进行修正:

式中:当预测值被高估时取“+”,当预测值被低估时取“-”。
4 实例分析
4.1 基础数据
某油田油气混输管道使用材质为API X60管线钢,外径340.8 mm,壁厚7.5 mm,投产后采用电阻探针和FSM 电场指纹技术对管道的腐蚀深度进行实时监测,由于GM(1,1)模型属于等间隔预测模型,故每30 d取一次平均腐蚀深度,其中该管道部分管段在第9 次检测后进行过一次大修作业,第10 次之后的增速较之前有所减缓,腐蚀深度实测值见表1所示。
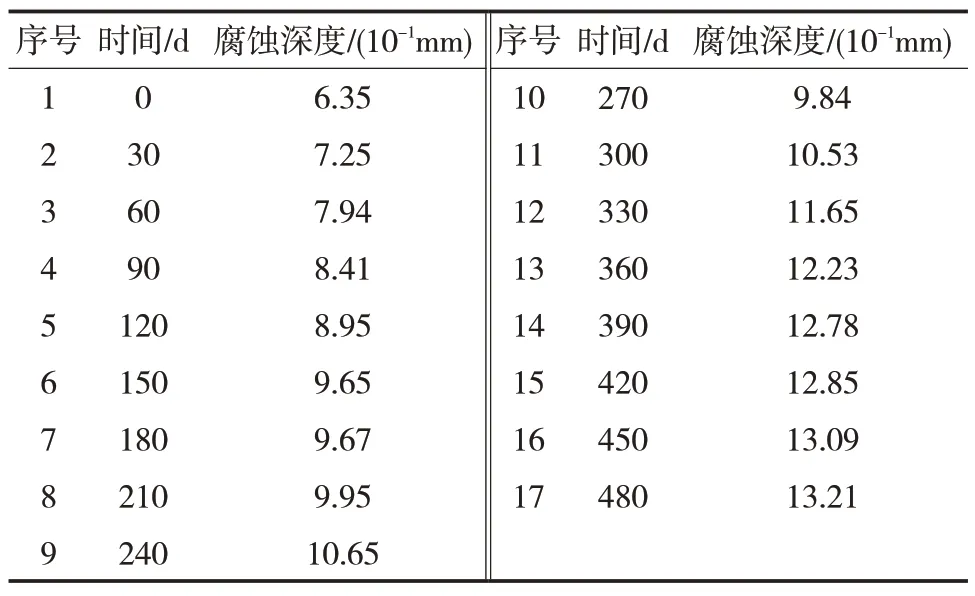
表1 不同时间的腐蚀深度实测值Tab.1 Measured values of corrosion depth at different times
4.2 优化GM(1,1)预测结果
根据前述模型,原始序列满足准指数和平滑规律,可以采用GM(1,1)模型进行预测。将前14组数据作为样本,预测15、16、17 组数据,采用Matlab 软件编程。经计算,传统GM(1,1)中a=-0.040 7,b=7.301 6,c=0.040 7,A=7.453 2,则无偏优化预测模型为

将前5 组数据作为初始序列进行等维信息更新。采用PSO算法对λ值进行寻优,其中搜索空间维度取1,粒子数取20,迭代次数1 000,惯性权重取0.2,学习因子均取0.5,选取均方根误差作为适应度函数。GM(1,1)、RGM(1,1)和RPGM(1,1)三种模型的预测结果对比见表2、图2。

表2 不同模型预测结果对比Tab.2 Comparison of prediction results of different models

图2 不同模型预测结果变化曲线Fig.2 Variation curves of prediction results of different models
从曲线走势看,GM 模型可较好地描述腐蚀深度发展趋势,GM(1,1)模型预测结果的残差范围为(-1.78,0.57),平均相对误差5.04%,相对误差较大的值出现在第10、11、12、13 次,管道大修造成了腐蚀状况的改善,但预测值与真实值严重偏离,说明了传统GM(1,1)模型对中远期预测的效果不好。RGM(1,1)模型预测结果的残差范围为(-0.91,0.51),平均相对误差4.05%,相比改进前,残差范围有所减小,预测精度提高了19.64%,说明RGM(1,1)模型对传统模型的优化效果有限。RPGM(1,1)模型预测结果的残差范围为(-0.27,0.51),平均相对误差1.94%,最大相对误差4.62%,预测精度较前两个模型分别提高了61.51%、52.09%,说明背景权值的选取对于模型预测精度影响最大。此外,GM(1,1)和RGM(1,1)的λ值均为0.5,而RPGM(1,1)模型通过不断迭代计算,共得到10 个最优λ值(前5 组数据为1 个λ值),分别为(0.458,0.437,0.462,0.477,0.488,0.558,0.642,0.412,0.315,0.333),其预测曲线变化趋势与实际曲线更为贴合,尤其对第10 次检测前后波动较大时的适应性较好。
4.3 RPGM-Markov链的腐蚀动态预测结果
利用Markov链理论对RPGM(1,1)模型的预测值进行修正,相对误差范围为(-3.22,4.61),序列均值u=0.32,标准差σ=2.34,采用均值-标准差分级法对相对误差序列进行状态区间划分(表3)。

表3 相对误差状态区间划分Tab.3 Division of relative error state interval
对表2 中RPGM(1,1)模型的相对误差状态进行统计,此时第14 组数据的后续状态未知,无法确定其向任一状态的转移概率,故该时刻不参与统计,得到转移概率矩阵P:

对于前14 组数据按照真实状态区间进行修正,以第2 次检测为例,该时刻处于E3状态,且RPGM(1,1)模型的预测值大于实际值,根据公式(10)对误差进行修正:

对于后3组数据,一方面求出对应数据的RPGM(1,1)模型预测值,根据第14组数据的状态采用转移概率矩阵预测后续的管道状态;另一方面确定误差符号的转移概率矩阵,根据第14 组数据的符号状态预测后续的误差符号状态(表4)。
依次类推,得到RPGM-Markov 链模型预测结果(表5)。该模型的残差范围为(-0.38,0.21),平均相对误差1.02%,与RPGM(1,1)模型相比,精度提高了47.42%,最大相对误差仅为2.89%,且在后3 组数据的预测中,相对误差大幅减少,证明Markov链可有效改善GM(1,1)模型对于中长期预测误差较大的缺陷(图3)。

图3 RPGM-Markov链模型预测结果Fig.3 Prediction results of RPGM-Markov Chain model
4.4 模型精度检验
为确定模型预测结果的可靠性,采用均方差比值f和小误差概率Δ 对模型的精度和可信度进行检验,f值越小、Δ 越大说明模型精度越高(表6)。其中,RPGM-Markov 链模型的预测精度等级为“好”,远高于其余模型的预测精度[11]。

表6 模型精度检验结果Tab.6 Test results of model accuracy
5 结论
RPGM(1,1)模 型 与RGM(1,1)、GM(1,1)模型相比,预测精度大幅提升,有效改善了数据波动对预测精度的影响,同时引入Markov链对未来时刻的状态进行预测,以相对误差为修正指标,对预测值进行修正,修正后结果与实际值更加吻合;该模型适用于具有指数变化规律、随机波动性较大的中远期事件预测,可通过动态模型对管道未来的腐蚀发生趋势进行预测,随机掌握腐蚀发展动态,为管道的进一步维护和检修提供理论依据和技术指导。

