数控机床“对称映射”热稳健性建模方法研究

骆 辉，路世青，冉 靖，吕世鑫，唐光元

(重庆理工大学 机械工程学院， 重庆 400054)

0 引言

数控机床的整体误差中，热误差占到了40%～70%[1-2]，热误差补偿对于数控机床性能提升至关重要。目前国际科研人员对此研究的主要方法是利用温度同热误差之间建立精度高、稳健性强的预测模型而加以对机床控制和补偿[3-10]，其理论核心是温度敏感点选择和建模算法与机床热特性的匹配性程度[11]。Shi等[12]提出采用模糊c均值聚类和相关分析方法选择温度敏感点，并引入邓恩指数确定最佳聚类组数，有效地抑制了温度测点之间的多重共线性问题。此外还有学者提出粗糙集理论结合灰色关联度算法[13]、模糊聚类结合相关系数算法[14]、平均冲击值法[15]等用于温度敏感点选择。Ramesh等[16-17]采用支持向量机算法进行建模。Miao等[18]提出利用模糊聚类结合灰色关联度算法对温度敏感点选择，使得温度敏感点优化至2个。随后，Miao等[19-20]提出了一种主成分回归(PCR)算法，相关系数结合岭回归算法等建模方法，消除温度变量之间多重共线性的影响并减少温度敏感点的变动性，并提出了完整的模型稳健性概念。模型稳健性表现为所建立的热误差预测模型在不同的工况下，依旧能展现出良好热误差预测精度，是衡量热误差预测模型效果的重要指标之一。Volk等[21]在CIRP综述论文中将模型稳健性概念作为机床模型的五大特征之一。Mayr等[22]提出了一种在五轴加工中心上的定期更新的自适应热误差补偿模型，且设置运动控制极限作为触发条件，当误差值超过运动控制极限时则加大采集频率以保证模型的精度。Zimmermann 等[23-24]提出自主更新建模输入参数的自适应热误差补偿模型以提高模型的长期有效性，提高生产效率。但是，实时更新的缺陷在于需要在线实时的测量标准件进行模型的重建，所以工况条件比较苛刻。

故此，本文以台中精机Vcenter-55数控加工中心与leaderway- 450数控加工中心为研究对象，针对温度敏感点变动性，提出了KWG计算温度敏感点的方法，有效降低温度敏感点的变动性。针对不同型号机械结构不同的机床热特性差异，导致直接使用常用的MLR建模算法建立的模型预测效果不佳的问题，提出“对称映射”稳健性建模方法，该方法通过对热误差数据进行对称处理之后再进行建模，MLR模型的预测精度上升约46.6%，其模型应用周期提升至6个月有效期。

1 热误差建模算法

温度测点的分类和优选可以降低各温度测点之间的共线性，提高模型的稳健性。本文通过K-means聚类算法对温度测点进行分类，将相关性强的温度数据分为一类。后续选择温度敏感点时就可以减少不同类的温度测点之间的共线性干扰，从而增强预测模型的稳健性。之后使用灰色关联度计算出各类中相对热误差权重最大的温度测点作为温度敏感点，用于建立预测模型。

本文针对模糊聚类结合灰色关联度算法[18]选择出的温度敏感点仍具有一定变动性的缺陷，提出K-means聚类算法结合灰色关联度算法进行温度敏感点的选择。

1.1 K-means聚类算法

K均值聚类算法(K-means clustering algorithm)是一种迭代求解的聚类分析算法。其一般通过欧氏距离进行分类的判定依据，通过多次的迭代至满足预定条件，从而获得最佳分类。

(1)

式中：xi表示x的第i个坐标;yi表示y的第i个坐标。

同时，为了进一步提高建模预测精度，尽可能让传感器中包含更多的热特性信息量，故采用邓式灰色关联度[25-26]在类中进行传感器优化选择，可进一步提高选择的传感器在模型中的权重影响。

1.2 建模算法

本文采用常用的MLR算法建模[19-20]，目的在于验证通过模型预测精度相互比对分析不同温度敏感点选择算法的优劣性，以及相互比对2种算法在不同规律的热误差数据下建模的精度与稳健性。

为验证所建立的模型预测精度效果，以残余标准差S作为精度评判标准，将各批次模型进行相互预测。而模型对各批次数据的预测残余标准差S的平均值Smean能够从整体上反映模型对全部数据的预测效果，因此可以用来表征模型的预测精度;S的标准差Sstd则反映了模型对其他批次数据预测效果的波动性，因此可以用来表征模型的稳健性。

预测残余标准差S的计算公式为:

(2)

Smean和Sstd的计算公式如下所示

(3)

式中：Si, j表示数据预测的残余标准差，K表示数据批次。

2 实验方案介绍

2.1 测量装置介绍

本文以Vcenter-55数控加工中心和leaderway- 450数控加工中心作为被测对象，实验方案以台中精机Vcenter-55数控加工中心为例，如图 1所示为Vcenter-55加工中心的正面图像，包括了机床整体、主轴箱、主轴前端、检验棒、位移传感器夹具等。其中leaderway- 450数控加工中心的实验方案与之相同。

图1 Vcenter-55数控立式加工中心

2.2 实验安排

各批次实验热误差测量过程参考国际标准 S0 230-3∶2020，机床主轴以恒定转速2 500 r/min空转运行，工作台沿X、Y轴向以恒定1 500 mm/min的进给速度进行往返运行，每运行5 min 采集一次温度和热误差数据，每批次实验时间持续6 h 之上。

位移采集使用的是电涡流位移传感器，通过位移传感器夹具固定在机床工作台上，在X轴与Y轴方向上各2个位移传感器，Z轴方向上一个位移传感器。温度采集选用的是DS18B20温度传感器，贴放在机床各热源位置[20]。

2.3 实验数据分析

根据文献[11]中提到数控机床热误差模型在不同温度区间内，建模预测效果差异显著。因此，为避免由温度区间导致的热误差模型效果下降带来的影响，本文选择全年环境温度24 ℃以下的多批次实验数据进行分析。下文中Vcenter-55加工中心选择了13批次实验数据，分别表示为K1～K13批次。Leaderway- 450数控加工中心选择了13批次实验数据，分别表示为K1～K13批次。

2.3.1温度数据分析

绘制Vcenter-55数控加工中心和leaderway- 450数控加工中心实测数据K1批次的温度变化趋势图，如图2、图3所示，可观察出各温度数据的变化规律随着时间缓慢上升，在机床热平衡之后趋于稳定。

图2 Vcenter-55 第一批次实验温度数据曲线

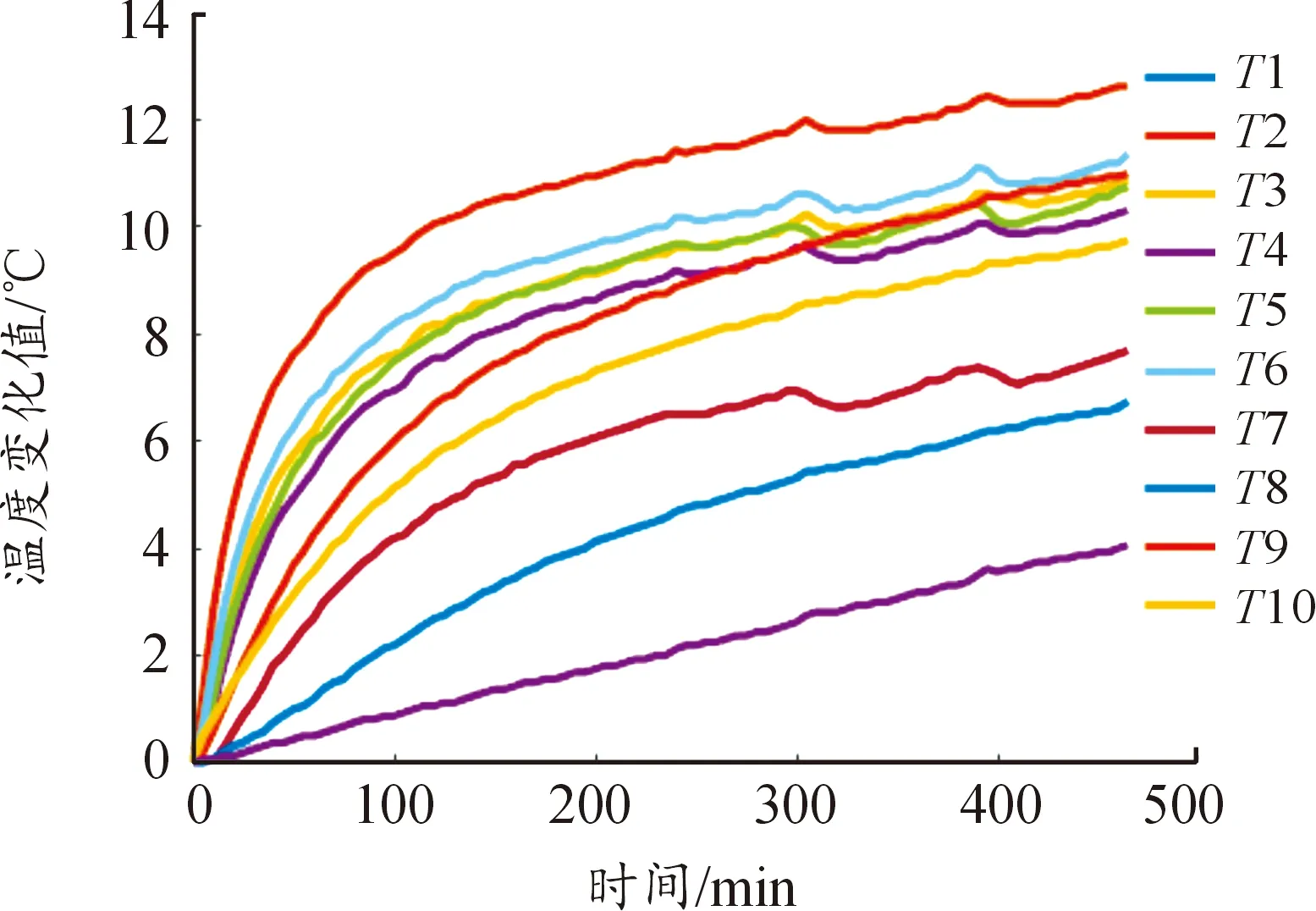
图3 leaderway- 450 第一批次实验温度数据曲线

不同型号的加工中心，其温度变化特性趋势基本一致。而其热变形特性具体如何，仍需进一步研究。

2.3.2热误差数据分析

因Vcenter-55和leaderway- 450数控加工中心在X轴方向与Y轴方向上机床结构近似，并与Z轴方向的热误差数据进行比较，X轴和Y轴的热误差较小，故主要对Z向热误差数据进行了分析。为分析研究对象的热误差变化趋势以及比较不同型号加工中心的热误差趋势差异，对Vcenter-55数控加工中心和leaderway- 450数控加工中心的所有实验批次的Z轴热变形进行绘制，结果如图4、图5所示。

图4 Vcenter-55数控加工中心Z轴热特性随时间变化曲线

图5 leaderway- 450数控加工中心Z轴热特性随时间变化曲线

由图4分析可知Vcenter-55数控加工中心13批次实验数据中主轴Z向热误差整体趋势为随着时间先上升后下降，在机床热平衡后逐步趋于平稳。图5反映了leaderway- 450数控加工中心Z轴方向的热误差变化趋势，是随着时间先上升后在机床热平衡后逐步趋于平稳。相比较后发现Vcenter-55和leaderway- 450数控加工中心Z轴方向上所呈现出来的热特性差异较大，而leaderway- 450这种热变形规律在目前为国际已发表论文中的主流热变形特征趋势[12，19-20,27-28]，本文将其称之为“常规热特性趋势图”。而将图4所示热变形特征趋势图称之为“非常规热特性”趋势图。

3 温度敏感点选择

温度敏感点的变动性对模型的精度与稳健性也有很大影响[19]，为免除建模算法以外的因素影响，本文采用KWG温度敏感点选择方法，进一步强化温度敏感点的稳健性，从而增强模型的预测精度与稳健性。

因此后文通过KWG方法进行温度敏感点选择结果参与建立预测模型，预测模型则为常见的MLR模型，敏感点选择如表1所示。

表1 使用KWG分别对不同型号机床热特性数据进行温度敏感点选择

4 热误差建模预测

本节基于KWG方法选择的温度敏感点建立了Leaderway- 450与Vcenter-55加工中心Z轴的热误差的多元线性回归模型。即分别对“常规热特性”与“非常规热特性”进行建模预测，结果分析发现相同的算法针对“非常规热特性”建立的模型精度与稳健性明显更差，无法满足工业应用需求。

为解决“非常规热特性”模型精度较差的问题，本文从算法与数据的适配性出发，提出了“对称映射”稳健性建模方法。并通过与直接建模的预测结果相比较，验证了“对称映射”稳健性建模方法建立的模型预测精度与稳健性更高。

4.1 热特性的直接建模

4.1.1针对“常规热特性”的预测建模

针对Leaderway- 450加工中心Z轴热误差数据所展现出来的“常规热特性”进行直接建模分析，即使用KWG方法选择的温度敏感点参与建立多元线性回归模型，如表2所示。

表2 “常规热特性”MLR模型

其中，模型相互预测之后的预测精度与稳健性分别是Smean=6 μm，Sstd=1.39 μm。

为了探究“非常规热特性”的建模规律，采用上述相同的方法对Vcenter-55数控加工中心热特性进行预测建模与分析。

4.1.2针对“非常规热特性”的预测建模

通过分别进行多元线性回归和岭回归建模并进行数据预测，建模情况如表3所示。

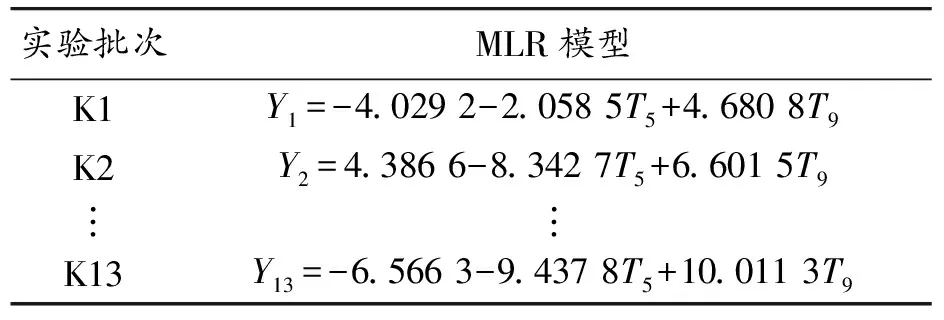
表3 “非常规热特性”的MLR模型

通过相互预测对评估模型的预测效果，并将“常规热特性”与“非常规热特性”通过Smean和Sstd分别评价模型的预测精度以及稳健性，详细数据如表4所示。

表4 “常规热特性”与“非常规热特性”直接建模的模型整体预测精度与稳健性 μm

通过表4可以分析得出，“非常规热特性”MLR模型精度劣于“常规热特性”MLR模型，且整体预测精度在8 μm以上，无法满足精度要求，对此本文通过分析数据变化趋势，基于稳健性建模理论，提出了“对称映射”稳健性建模方法。

4.2 “非常规热特性”的稳健性建模

4.2.1“对称映射”稳健性建模分析

通过绘制“非常规热特性”K1批次数据Z向热误差的MLR模型曲线,即由图6可得出如下结论与看法：Z轴方向的热误差变化趋势呈现出随着时间先上升然后下降随后趋于平稳的趋势，MLR模型与热误差数据的契合度不高，模型整体呈现出随着时间先快速上升，然后略微下降后就趋于平稳，这使得图中虚线框中的热误差数据转折点处模型的残差值较大，达到10 μm。

图6 “非常规热特性”K1批次实验Z轴热误差MLR模型曲线

故提出采用“对称映射”数据处理方式，将数据进行翻转处理，使其整体趋势更加平滑，随后利用“对称映射”数据进行建模，再将模型以相同的方式进行翻转处理，最后将翻转后的模型同实验测量数据进行比较。发现建模效果显著提升，残差由原来的正负10 μm的波动提升至正负5 μm的波动，如图7、图8所示。

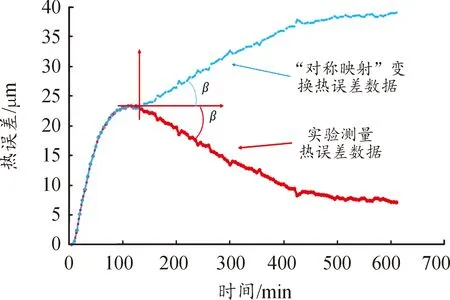
图7 “对称映射”数据处理曲线

图8 “对称映射”处理后的MLR模型曲线

因此，本文根据上述“对称映射”稳健性建模方法应用于“非常规热特性”其他批次数据进行建模预测与分析。

4.2.2“对称映射”稳健性建模方法验证

将“非常规热特性”的K1～K13批次实验Z轴的热误差数据全部进行“对称映射”数据处理，如表5所示，建立MLR模型，并将翻转MLR模型同实验测量数据通过S值进行相互预测比较。

表5 基于“对称映射”处理的“非常规热特性”的MLR模型

通过比较分析图 9和表6后发现，直接使用MLR建模算法对于“非常规热特性”趋势下的热误差预测效果不佳且稳健性差。而使用“对称映射”稳健性建模方法进行MLR模型建立，其预测精度与稳健性都得到了较大提升，该方法通过对热误差数据进行相应处理之后再进行建模，其MLR模型的预测精度上升约46.6%，稳健性提升60%。

图9 “对称映射”数据处理后MLR模型相互预测曲线

表6 “非常规热特性”采用不同建模方法的模型整体预测精度与稳健性

MLR模型虽然应用广泛，但因其稳健性问题，大多数情况被摒弃。对于本文采用“对称映射”方法进行建模时，却意外发现MLR算法预测精度也得到了相应的提高，稳健性也有所提高。因此本文得出结论：对于许多算法在面对特殊规律的数据时，可以让算法产生变化使其重新获得有效的应用。通过本文的思路与方法，拓展了MLR建模算法的有效应用范围，使其能更好地使用。

5 结论

针对数控机床温度敏感点存在随着季节变化而变动，导致预测模型的精度随之改变，模型稳健性下降的问题。提出了使用KWG方法，优选出稳健性较高的温度敏感点，并进行实验证明KWG方法选择的温度敏感点变动性低。同时针对研究对象所表现的不同于一般规律的热特性提出了“对称映射”稳健性建模预测方法，解决了特殊热变形规律与现有模型算法稳健性适用范围不匹配的问题，有效提高了模型的预测精度与稳健性。本文使用“对称映射”稳健性建模预测方法后，该方法通过对热误差数据进行相应处理之后再进行建模，其MLR模型的预测精度上升46.6%，稳健性提升60%。

此外，目前大多数研究团队面对数据建模时都具有一定的盲目性，导致选择的建模算法与数据的适用范围不匹配等问题。本文通过“对称映射”稳健性建模方法研究发现不同的建模算法对参与建模的数据存在“适配性”问题，当参与建模的数据与建模算法“适配度”越高，所建立的模型精度会更高。

对于算法适配性的问题，后期将继续进行研究。