卡尔曼滤波下混沌噪声背景中微弱脉冲信号的检测
苏理云,石 林
(重庆理工大学 理学院, 重庆 400054)
0 引言
微弱信号是被深埋在噪声背景下极其微弱的有用信号,它可以从相对性(信号幅值相对于噪声很微弱,如在早期故障阶段的机械设备,各类对应故障的特征信号以某种方式混合在正常信源信号中,导致特征信号十分微弱;而设备在工作时,又会被强噪声干扰)和绝对性(信号幅值极小)这2个方面理解[1]。随着科学与技术的不断发展,人们对被噪声掩盖下的微弱信号(如微振动、弱磁等)的检测越来越重视[2]。微弱信号的检测主要有2个特点:第一,在信噪比(signal-to-noise ratio,SNR)较低的情况下检测微弱信号;第二,要求检测具有时效性,但工程中采集的数据长度或持续时间会受到一定的限制[3]。混沌时间序列的预测是基于Takens定理[4]的理论依据上进行的,大多微弱信号的检测[5-15]都是通过解析噪声和信号的不同之处,抑制噪声,剥离出微弱信号。卡尔曼滤波算法被广泛用于通信、导航以及跟踪领域,它可以对采集的实时数据进行动态处理,利用线性系统观察和检测输入、输出数据,最后得到系统的最优估计[16]。为了更好地抑制混沌噪声,提高信号的检测能力,构建了一种基于卡尔曼滤波的混沌噪声背景下微弱脉冲信号的检测模型。首先,对观测信号建立一步预测模型,进行单步预测,得到预测误差。然后,给定一个阈值,从预测误差中检测微弱脉冲信号是否存在。
1 基于卡尔曼滤波的微弱脉冲信号的检测
关于混沌噪声背景下微弱脉冲信号的检测,可以表示为以下的假设检验问题:
(1)
其中:y(t)为观测信号,c(t)为混沌噪声背景信号,s(t)为目标信号且与混沌噪声背景下的信号c(t)独立,N(t)表示均值为0的白噪声。
由于目标信号s(t)是微弱脉冲信号且被混沌噪声背景信号c(t)淹没,要想更好地剥离出目标信号s(t),就要去除混沌噪声背景信号c(t)的干扰,则上述的假设检验问题就可以转化为:
(2)
1.1 卡尔曼滤波
卡尔曼滤波的循环递归过程如下:
2) 在第t步:
3) 以观测的yt更新αt:
4) 获得Pt:
5) 向前投影:

带有线性趋势的ARIMA模型为:
yt=βt+αt+εt
(3)
αt~ARIMA(0,d,0)(p,0,q)
状态空间模型为:
yt=Ztαt+εt,εt~N(0,Ht)
(4)
αt+1=Ttαt+Rtηt,ηt~N(0,Qt)
(5)
a1~N(a1,P1),yt:p×1,αt+1:m×1,ηt:k×1
其中:Zt、Tt、Rt为确定模型形式的参数,而a1、P1、P1linf为初始值;a1为可选的m×1矩阵,给出初始状态向量α1的期望值;P1为可选的m×m矩阵,给出α1的协方差矩阵,在漫反射情况下,P1的非漫反射部分;P1linf为可选的m×m矩阵,给出P1的漫反射部分,其为对角矩阵,对角元素上的矩阵对应于扩散初始状态,如果P1inf(i,i)>0,则P1对应的行和列应为零;而Ht和Qt为待估计的参数。
1.2 微弱脉冲信号的检测
结合状态空间模型,利用卡尔曼滤波得到了单步预测误差,怎样在这些误差中快速准确地找到被淹没的微弱脉冲信号,就需要给定一个判断规则。这里,给定一个阈值:
(6)


图1 微弱脉冲信号的检测流程框图
2 仿真实验

Lorenz方程为:
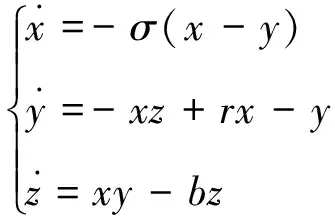
(7)
其中:σ=10,b=8/3,r=28。
初始条件设定为:x=1,y=1,z=1,采样时间t=0.01 s,产生了10 000个数据点,选取第二个分量作为混沌噪声背景c(t)。为了确保系统完全进入混沌状态,这里舍去了前面3 000个点,选取4 000个连续序列作为混沌噪声背景,记为{c(t),t=1,2,3,…,4 000}。
微弱脉冲信号由2个周期微弱的脉冲信号叠加组成,即有s(t)=a1s1(t)+a2s2(t),其中:
(8)

(9)
生成长度为4 000的时间序列,记为{s(t),t=1,2,3,…,4 000},这里,T1=550,T2=650,a1=2,a2=3。此时,信噪比为-80.12 dB。


图2 信号时序图及单步预测误差
基于卡尔曼滤波建立的单步预测模型为带有线性趋势的ARIMA模型yt=βt+αt+εt,αt~ARIMA(0,1,0)(4,0,5)和状态空间模型,给定的初始值为:
由图3可知,不管是有线性趋势的ARIMA模型,还是状态空间模型,经由卡尔曼滤波进行估计之后的效果都非常好,估计值与观测值几乎没有差别,表明了卡尔曼滤波的适用性和优越性。
由表1的检测结果可知,15个微弱脉冲信号中有11个被模型检测正确,t为1 650和3 300时存在的微弱脉冲信号未被模型检测到。模型错误检测了2个不存在的信号,t为686和3 252时没有信号但模型错误检测出了信号的存在。

图3 预测误差与观测信号曲线

表1 有线性趋势的ARIMA模型的检测结果
由表2的检测结果可知,14个微弱脉冲信号中有11个被模型检测正确,t为1 650和3 300时存在的微弱脉冲信号未被模型检测到。模型错误检测了1个不存在的信号,t为686时没有信号但模型错误检测出了信号的存在。表3为不同模型检测数量统计,表4为不同模型的检测精度。

表2 状态空间模型的检测结果

表3 不同模型检测数量统计

表4 不同模型的检测精度
3 结论
基于卡尔曼滤波,提出了一种混沌噪声背景下微弱脉冲信号的检测方法。在信噪比为-80.12 dB时,基于卡尔曼滤波的状态空间模型检测精度高达91.67%,F1得分达到了0.88,一般的ARIMA模型和基于卡尔曼滤波的有线性趋势的ARIMA模型的检测精度都为84.62%,F1得分都是0.85,但基于卡尔曼滤波的有线性趋势的ARIMA模型的均方根误差(RMSE)是3个模型中最小的,为0.02。综上,卡尔曼滤波在检测被混沌噪声淹没的微弱脉冲信号上具有极大的适用性和优越性,检测精度提高了8.33%,检测性能提高了4.00%。

