一阶全偏联系数的计值公式及其应用
刘宗宝 LIU Zong-bao;陆广地② LU Guang-di;赵克勤 ZHAO Ke-qin
(①江苏联合职业技术学院宿迁经贸分院,沭阳 223600;②江苏科技大学计算机信息与技术学院,镇江 215600;③诸暨市联系数学研究所,诸暨 311800)
0 引言
系统是客观存在的,具有普遍性。从系统组成要素的性质来看,可以划分为自然系统和人造系统。自然系统是由自然物组成的,它的特点是自然形成的,如生态系统、星际系统等;人造系统是人们出于某种目的而制造的系统,如生产系统、交通系统、商业系统、管理系统等。还有从系统与环境的联系程度来看,可以划分为封闭系统和开放系统;从系统的状态与时间的关系来看,可以划分为静态系统和动态系统等等。无论是何种分类的系统,它们都具有以下几个共同的特征:整体性、层次性、目的性和适应性。系统总是在相互合作和不断演化的过程中呈现的耗散结构。长期以来科技工作者总是尝试捕捉大千世界的变化过程和演化强度,在变化的过程中把握其中的不变性。我国学者赵克勤先生1989年创立的集对分析理论为这方面研究提供了新思路;用一个联系数刻画一个系统中部分要素正常、部分要素异常、部分要素反常的状态,简称同异反系统。联系数的偏联系数是刻画这个系统部分要素正常、部分要素异常、部分要素反常这三部分之间相互递进和衰减演化的伴随函数,目前已得到广泛应用,如覃杰、赵克勤(2007)将偏联系数应用于医疗质量发展趋势分析,王传斌、王继顺(2011)将偏联系数应用于对高职教师执行力的潜在分析,马晓燕等人(2012)将偏联系数应用于公众信任度潜在分析,陆广地等(2015)将偏联系数应用于高校评价的排序与聚类分析,晏燕等(2018)把偏联系数用于隐私风险态势评估,门宝辉(2022)将偏联系数应用于地下水开采评估,陈微,赵克勤(2022)将偏联系数应用于学生近视分析,杨红梅(2019)给出了多元联系数的偏联系数计算方法,于2021年出版专著《偏联系数的哲学原理与应用》等。但三元联系数的一阶全偏联系数中含有不确定性示性系数i和i,如何根据问题的已知条件客观地给定i和i的值,直接影响到一阶全偏联系数的计算结果和联系数系统的演化趋势判定。赵克勤(2005)、杨红梅(2019、2021)、陆广地(2022)相继给出了不同的取值方法。但是最近的研究表明,三元联系数的一阶全偏联系数的不确定性示性系数i和i还存在新的算法,本文给出了这一新算法的原理,进而给出了三元联系数的一阶全偏联系数计值公式,用实例说明这一新公式的应用。
1 三元联系数及其一阶全偏联系数计值公式
1.1 三元联系数
三元联系数是集对的一种特征函数,其一般形式为μ=a+bi+cj,其中a、b、c∈[0,1],i∈[-1,1],j=-1,μ∈[-1,1](1)
由(1)式知,联系数具有以下性质。
<性质1>系统性。联系数μ包含a,bi,cj3个联系分量,且分别处于+1,[-1,1],-1三个层次,“+”号表示a,bi,cj具有3个层次的空间联系,i是b的示性系数,表明b的取值具有不确定性,j是c的示性系数,表示c与a具有正负对立性,在忽略不计i、j的示性系数意义时,“+”号表示单个联系分量与三元联系数整体的联系;a,bi,cj分别称为三元联系数的同部、异部、反部。
<性质2>可计算性。从数学角度看,式(1)是一种结构函数,具有可计算的特点:既可以用来表征一个现实系统既有确定性测度a和c,又有不确定性测度bi的状态,又可借助适当的伴随函数,展示式(1)联系数所示系统状态的演化趋势。
1.2 三元联系数的偏联系数
由文献[3]知,三元联系数的偏联系数由赵克勤先生于2005年提出,其概念的形成和相应的计算规则主要依据联系数的上述2条性质。具体又分成三元联系数的一阶偏正联系数和三元联系数的一阶偏负联系数,以及三元联系数的一阶全偏联系数,这些概念用如下3个定义体现。
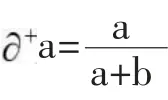
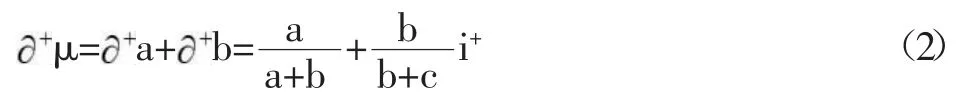
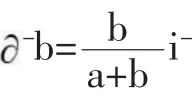
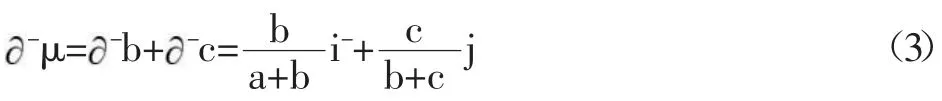
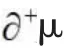
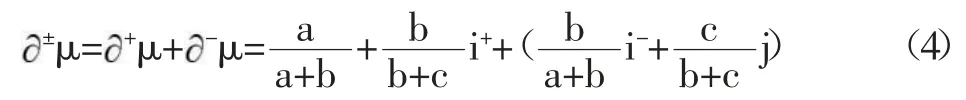
以上式(4)中,j=-1是式(1)所示三元联系数μ=a+bi+cj在正负型对立问题中规定的取值,但i与i如何在i的定义域[-1,1]中取值,则是一个有待于进一步具体分析的复杂问题。
1.3 i与i的取值
赵克勤先生在2022年8月6-10日网络在线举办的全国集对分析第16次学术研讨会上提出了(5)式中i与i的一种新算法如下:
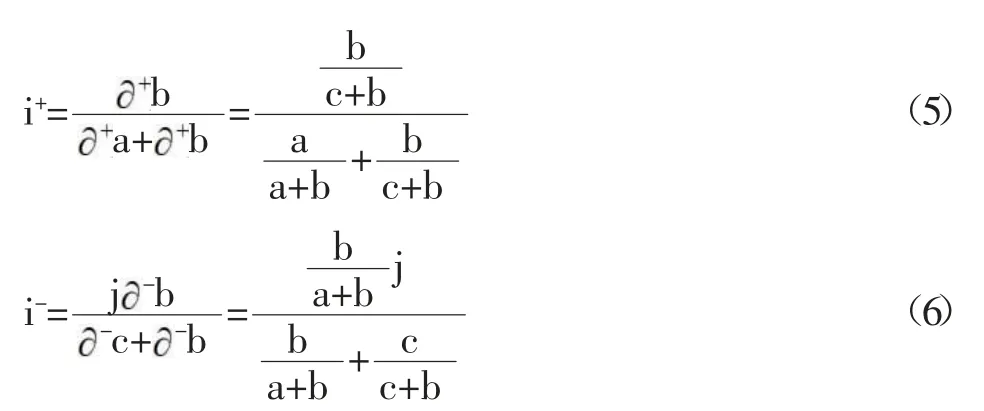
原理如下:
把(4)式所示的三元联系数μ=a+bi+cj的一阶全偏联系数简化为具有正极和负极两个极性的一个线性系统S^。

图1 线性系统的两种工作状态(正常+1与反常-1)表示

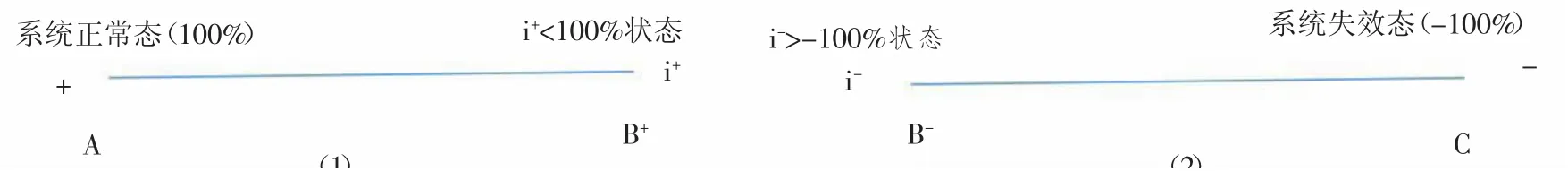
图2 线性系统SAC^分解成两个子系统SAB^和SBC^的图示
再把图2(1)与(1)式相比较,其演化分量的关系可以用如图3(1)所示。

图3 线性系统SAC^分解成两个子系统SAB^和SBC^的演化分量图示
根据量子纠缠、对立互补的思想,系统表面层是从B向A方向运动,但其微观层是伴随对立状态,i起调节作用,所以i在微观上遵从A向B作反向运动,按照其运动方向的“比例原则”进行计算。由图3(1)可知i应该按照上式(5)进行计算。
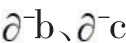
需要指出的是,式(6)中的分子中给出示性系数(jj=-1),体现了式(6)的绝对值是其演化内容包含为反方向时的强度;至于式(5)中的i本来是正向,所以不必要添加表示正方向的示性系数+1。
把式(5)式(6)代入式(4),得到
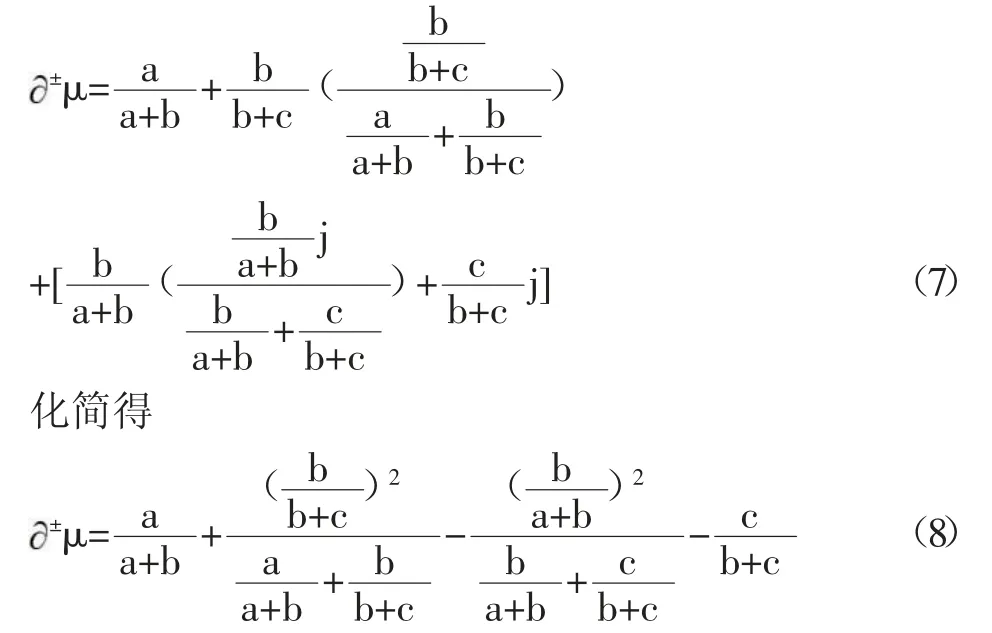
2 应用举例
例:为了便于对照,这里引用文献[7]中的例题,其原始数据全部在文献[14]中,是我国曾经的985工程建设高校中的8所学生满意度调查数据处理成标准化的三元联系数之后,再按照本文的公式(2)(3)联系数处理如表1所示。
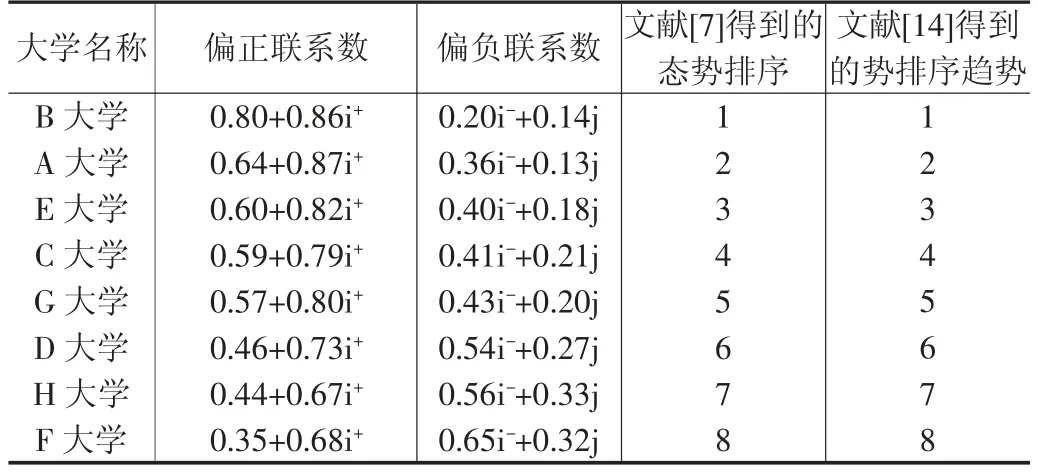
表1 学生对8所著名高校本科教育评价满意度的偏联系数态势排序
将表1中联系数中i与i使用本文给出的算法代入算出偏正联系数、偏负联系数,按照公式(4)求出全偏联系数值,再据其值进行态势排序,与文献[14]进行比较,如表2所示。
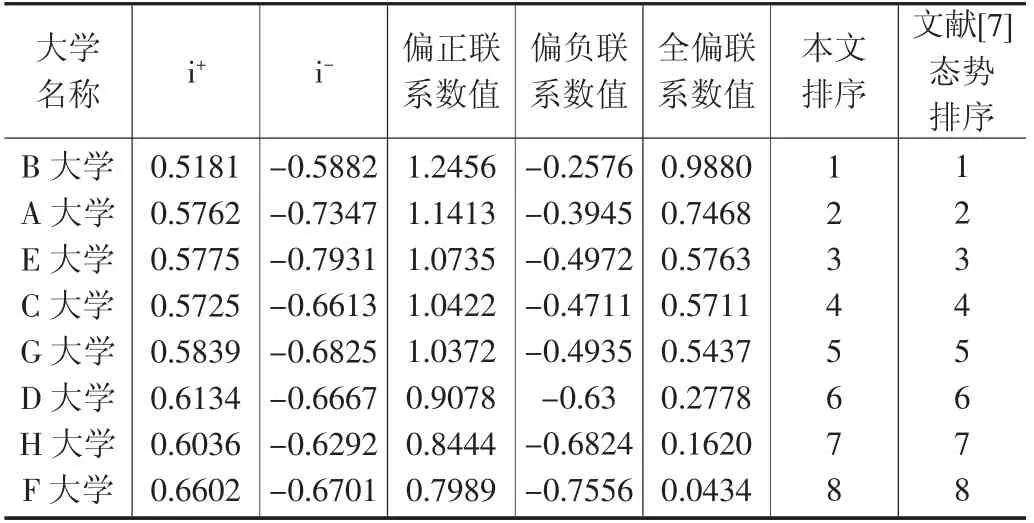
表2 学生对8所著名高校本科教育满意度的偏联系数中i+、i-按本文取值的态势排序
从表2可以清楚地反映出,本文对i和i的新方法与文献[7]的态势排序具有内在的一致性,差别在于文献[7]把三元联系数μ=a+bi+cj中的i看成是不确定性联系分量b的示性系数,本文则从三元联系数μ=a+bi+cj整体角度对i取值,殊途同归,相互证明了两种取值方法的科学性。
3 讨论与结论
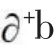
3.2 结语 本文给出三元联系数的一阶全偏联系数计值公式及其原理,用实例说明其应用的有效性。但三元联系数已应用到水文水资源、地质矿山、交通物流、社会经济等不同领域,不同领域不同问题中的三元联系数有不同的物理意义,如何根据不同领域不同实际问题要求计算三元联系数的一阶全偏联系数数值,需要不同领域专家根据不同问题要求从不同角度探索,本文提出的的计算公式仅作为一家之言,作为引玉之砖供有关专家参考。

