船载惯性测量单元姿态信息优化方法

靳建波，孔令哲

(1.西安交通大学，西安 710049；2.中国电子科技集团公司第三十九研究所 陕西省天线与控制技术重点实验室，西安 710065)

0 引言

我国地球同步卫星技术的进步使得卫星通信资源越来越丰富多样，互联网的发展让大数据以及物联网也得到了广泛应用，地面有线基站通信模式无法实现的海洋通信网必然要通过卫星通信实现，因此船载通讯设备即动中通的需求也得到了极大释放。基于微电子系统(micro electro mechanical systems，MEMS)的惯性测量单元(inertial measurement unit，IMU)是船载动中通天线系统的核心器件，是保障动中通设备稳定跟踪的关键所在[1]。一般情况下，惯性测量单元通过卡尔曼滤波法[2-5]将三轴测量角速度与三轴测量加速度信息融合，获得相对准确的大盘动态姿态信息，但在实际动态使用过程中，仅通过此法获得的大盘信息应用于船摇隔离的效果并不理想，通过机理分析及大量数据采集佐证，是由于三轴测量加速度在测量单元空间运动时被其它加速度所污染而导致的测量信息偏差所致，为便于区分，这类影响姿态测量的加速度统一称为有害加速度[6]。本文将分析有害加速度的产生原因，对测量载体姿态欧拉角信息的影响，提出了一种有害加速度的滤除方法，进一步提升了微电子传感器对载体姿态信息的测量精准度。此滤除方法可拓展应用于多种存在干扰信息的设备，尤其为动中通系列产品及类似设备的推广和应用提供了便利。

1 卡尔曼滤波法

要想弄清有害加速度是如何影响惯性测量单元姿态测量信息的，首先就要了解惯性测量单元姿态测量的基本算法，即卡尔曼滤波法。卡尔曼滤波法的原理是通过多通道传感器测量，在预先知晓各测量方案噪音状态的情况下得到概率意义上的原始测量数据[7]。为配合卡尔曼滤波法的应用，需要构建不同于直接测量通道的其它载体姿态测量通道。在惯性测量单元3个标志向量X、Y与Z轴上分别安装角速度计和加速度计，进行一步预测，并结合卡尔曼滤波算法，通过载体姿态旋转四元数[8]的状态方程，比较预估姿态和实际测量姿态得到概率意义上的低噪音、高精度姿态信息，从而获得准确的滤波结果。卡尔曼滤波过程可分为5步：

1)姿态预估

设在Tk-1时刻，即在无载体姿态测量信息时，由姿态旋转四元数的状态方程运算获得姿态信息预估：

(1)

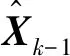
2)一步预测误差方差阵

(2)

其中，Qk-1为系统过程的协方差，为干扰矩阵，和测量单元电子器件测量精度和安装精度有关，可预先测得[9]，Pk-1为Tk-1时刻的预测误差方差阵，Pk,k-1为下一时刻的预测误差方差阵。

3)滤波增益矩阵

(3)

其中，Hk为观测阵，此算法中为单位对角阵。Kk是卡尔曼增益。

4)状态矩阵估计

在Tk时刻，由测量姿态输出和预估值，通过矩阵运算，得到概率意义上的修正真值：

(4)

5)估计误差方差阵

(5)

其中，I为单位对角矩阵。

经过以上5步，可以准确的获得经过卡尔曼滤波法处理的以四元数形式表述的载体姿态信息，进而获得旋转矩阵与姿态欧拉角信息。

2 有害加速度分析

基于三轴角速度、三轴加速度测量原理的惯性测量单元(常规捷联惯导)，均采用卡尔曼滤波法将旋转四元数姿态积分矩阵与测量的重力加速度矢量标量数据融合，以获得高机动性的动态姿态信息。由于姿态信息是以三轴加速度测量的重力加速矢量标量信息作为收敛依据，故而三轴加速度测量重力加速的准确与稳定性是惯性测量单元姿态信息准确与稳定性的重要依据。但在实际使用中，惯性测量单元的空间运动并不是理想的质心转动，在大地惯性系里，其空间运动速度的大小及方向的改变同样会产生加速度。因此，除大地重力加速度外，三轴加速还会测得由于空间运动改变而产生的其他加速度。这些加速度的参与将会干扰姿态收敛，影响姿态信息的准确性，在姿态收敛计算过程中，他们统称为有害加速度。

船载动中通使用过程中，惯性测量单元必然参与空间运动，只要运动形式发生改变，就会存在有害加速度夹杂在测量重力加速度数据中干扰姿态收敛计算。为便于分析，现将有害加速度依据其作用形态分为两类。一类有害加速度是相对大地测量系相对静止的，如载体空间直线运动加速度，此类加速度与重力加速度空间相对静止，其作用并不影响惯性测量单元的姿态变化。因此，通过三轴角速度与三轴加速的测量信息并不能将其分离出来，即可观不可控[10]。所幸的是，这类有害加速度在船载动中通真实使用过程中多为瞬时加速度且数值不大，可通过合适的卡尔曼滤波系数降低其干扰。另一类有害加速度是相对惯性测量单元测量系相对静止的，如船摇过程中的法线加速度、切线加速度。此类加速度在船摇过程中持续周期性干扰测量数据，影响卡尔曼滤波法收敛过程，是影响惯性测量单元动态数据的主要因素。为提升系统性能，降低成本，此类有害加速度需要从三轴加速度测量信息中滤除。

不失一般性，设空间角速度矢量为ω，空间角加速度矢量为α，瞬时测量系旋转半径为r，则依据理论力学转动刚体运动模型[11]可知瞬时旋转加速度矢量a为

a=α×r+ω×v

(6)

其中，v为瞬时空间速度矢量，与角速度及旋转半径关系为

v=ω×r

(7)

即

a=α×r+ω×(ω×r)

(8)

如此时惯性测量单元测得的三轴角速度为ωx、ωy与ωz，微分三轴角加速度为dωx、dωy与dωz，瞬时测量系旋转半径为rx、ry与rz。则通过线性矩阵叉乘运算[12]有

(9)

其中at为切向加速度矢量，an为法向加速度矢量。由此可见，在瞬时测量系旋转半径已知的情况下，可通过三轴角速度信息将有害加速度从三轴加速的测量信息中分离出来，实现滤除此类有害加速度的目的。

但在实际应用中，横摇、纵摇的测量系旋转半径与船载动中通安装高度及船身吃水面相关，偏航的角的旋转半径与运动半径相关，因此测量系旋转半径是不可直观获得的，为滤除此类有害加速度还需通过数理统计[12]法计算。

3 有害加速度滤除法

空间旋转所产生的有害加速度与旋转速度及旋转半径有关，通过惯性测量单元可以获得旋转速度信息，但旋转半径是不可测量信息。不失一般性，设t0时刻，在惯导测量系下真实姿态矩阵为M0，本地重力加速度为g，测量加速度为G0，旋转半径为r，有害加速度计算矩阵为Q0。则有

G0=M0g+Q0r

(10)

随后的t1时刻为

G1=M1g+Q1r

(11)

由四元数积分计算可知

(12)

即

G1=Ω0(M0g)+Q1r

(13)

如令t0时刻姿态表征向量M0g为P0，则以此类推，随后ti时刻有

(14)

当采样周期短，被测姿态运动为自然运动时。我们可以认为相邻的两个采样时刻害加速度相同，则有

(15)

即通过姿态运动过程中理论加速度的变化与实际测量的加速度变化求得期望姿态表征向量。但鉴于噪音干扰以及采样周期短使得测量的加速度变化淹没于噪音中，因此需采用高斯最小二乘法[13]通过大数据计算t0时刻姿态表征向量P0。经过一段时间的测量数据采集，构建高斯统计矩阵有

(16)

等式两侧同时乘以高斯因子矩阵

(17)

则有

(18)

以上信息均可由惯性测量单元测得，从而计算出数理统计意义上的t0时刻姿态表征向量P0。由于t0时刻为过去时刻，因此，当前ti时刻的姿态表征向量为

(19)

表征向量Pi替代卡尔曼滤波法中的Gi参与姿态计算，滤除了有害加速度的干扰，可提升了姿态欧拉角信息的准确性。

4 有害加速度滤除效果

用实验对比数据验证船载动中通惯性测量单元有害加速度滤除法的效果。试验方法如下，在测试转台上架设半径为1.2m的延长臂，将自研惯性测量单元安装在臂的远端。为便于对比，测试转台仅方位轴做周期为5s，幅值为15°的正弦运动。 将未滤除有害加速度的解算姿态欧拉角、滤除有害加速度后的解算姿态欧拉角以及转台轴角信息实时纪录。

其中姿态欧拉角横摇对比信息如图1所示。

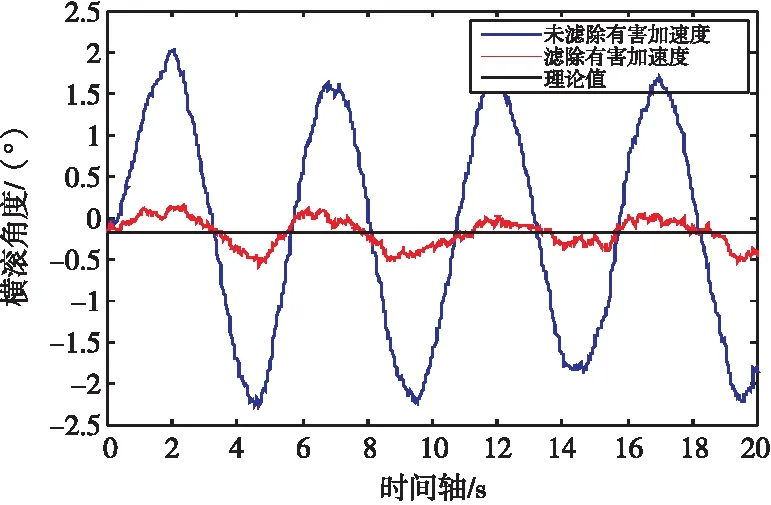
图1 姿态欧拉角横摇对比信息图Fig.1 Gesture Euler angle swings sideways to compare infographics

姿态欧拉角俯仰对比信息如图2所示。虽然船载动中通惯性测量单元有害加速度滤除法不能完全消除有害加速度对姿态欧拉角的干扰，但可最大程度抑制有害加速度对姿态欧拉角的影响，进而提升了系统的空间指向精度，如系统配合和信号跟踪等有效修正手段实现对目标的真实位置闭环，则能大大提升船载动中通系统的适应性。

图2 姿态欧拉角俯仰对比信息图Fig.2 Posture Euler angle pitch comparison infographic

5 结论

船载惯性测量单元姿态信息优化方法通过数值分析[14]，将干扰加速度从惯性测量单元三轴加速度测量信息中滤除，使测量所得的三轴加速度更接近于真实的本地重力加速度，提升了惯性测量单元反馈信息的真实性，降低了测量姿态欧拉角与真实姿态信息的偏差，进而提高了船载动中通天线空间指向精度，增加了船载卫通系统的环境适应性，达到了预期的控制效果。由于海洋中船载通信系统工作环境的复杂性和干扰的不确定性，需要对惯性测量单元做更多的测试研究，以扩展惯性测量单元的适用范围。