法塔莫干纳现象的形成机理及再现实验

陈佳彬，徐 强，王 巍，钟 鸣，陆建隆

(1.南京师范大学 教师教育学院，江苏 南京 210023；2.南京师范大学 物理科学与技术学院，江苏 南京 210023)

“飞翔的荷兰人”是一则流传于欧洲民间的传说.据传一艘荷兰军舰在好望角外遭遇风暴失事，同行的船经受住了风暴，随后到达好望角.但是在这些船只整修好返回欧洲的途中，在同一地点再次遭受到猛烈的暴风雨的袭击.值夜的水手看到，有一艘倒立的船若隐若现地朝着他们撞过来，一名水手确定这艘船正是在前一场风暴中失事的荷兰军舰.但是在风暴停止后，黑云似的军舰幻影就消失了.这个幻影从此就被人们称作“飞翔的荷兰人”.

对于这个传说的记载与解释有很多.根据“飞翔的荷兰人”虚幻、倒置、幻象重叠等特点，给出的最有可能的解释就是法塔莫干纳现象.这个幻影实际上是一艘因距离遥远而看不见的船在特定的大气条件下由于光的折射和全发射而形成的倒立多重虚像.据说不久之后，船长和水手们也确实看见了这艘船.

1 法塔莫干纳现象理论分析

1.1 法塔莫干纳现象形成的物理机理

通常一般形式的海市蜃楼是远处物体经过海面作用后形成的单个幻象，这个幻象称为蜃景.出现蜃景的原因是在太阳光照射等外界因素的影响下，空气的温度在不同高度的空气层中呈梯度分布，称为逆温层，由于冷空气密度大，折射率大；热空气密度小，折射率小，逆温层中气温递增或递减的梯度分布会导致空气密度和折射率的梯度分布，即不同高度的空气温度不同，密度不同，折射率不同[1].当物体发出的光线穿过不同高度的空气层时，由于光的折射发生弯折，最后进入人眼.我们的大脑认为光线总是沿直线传播，看到的物体就会偏离原位置.根据蜃景位置的不同可以分为上现蜃景和下现蜃景，幻象出现在原物上方就称为上现蜃景，出现在物体下方即为下现蜃景.图1为上现蜃景示意图，横线代表空气中的逆温层，带有箭头的线段为光线的轨迹.

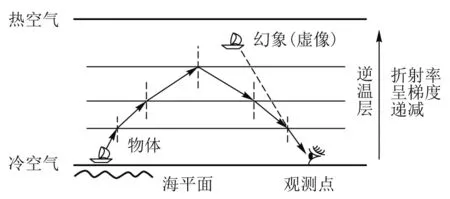
图1 普通海市蜃楼光路图(上现蜃景)

法塔莫干纳现象实际上就是一种形态复杂的海市蜃楼，在海面、陆地、极区都可以形成.图2是法塔莫干纳现象形成的示意图，可以把它归为一种复杂形式的上现蜃景.法塔莫干纳现象和一般形式的上现蜃景相比，除了需要具有温度梯度的逆温层存在(即存在折射率梯度)外，还需要在逆温层内存在折射率的跳跃变化[1].当逆温层内存在一层相较于下方(较冷而密度较大的空气)明显温暖的空气时，逆温层就会被分为两个小层，小层之间出现分界面.当存在多层这样的暖空气时，原来的逆温层就会演化为“逆温层——分界面——逆温层——分界面”这种逆温层与分界面交替出现的分布.

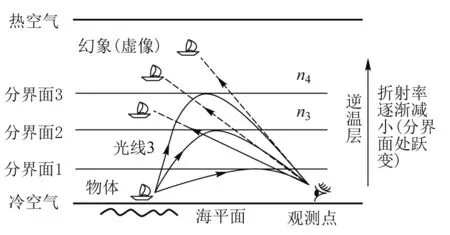
图2 法塔莫干纳现象光路图

如图3所示，横坐标为空气折射率，纵坐标为逆温层的高度，由图可见形成法塔莫干纳现象时逆温层中空气折射率随高度变化的特点，即在分界面处折射率出现跳跃递减.原本逆温层内折射率自下而上递减，但是由于分界面的存在，空气折射率在小层分界面处折射率跳跃式减小，在各小层内部梯度递减，小层与小层之间的折射率存在明显差异.

图3 法塔莫干纳现象形成时空气折射率随高度变化示意图

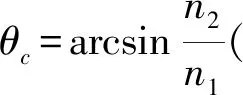
折射率的跃变是形成法塔莫干纳现象的必要条件，它依赖于逆温层的形成.常见的情况是空气容易形成逆温层，而在逆温层内形成折射率跃变的分界面并不容易，这也是法塔莫干纳现象不常见的主要原因.法塔莫干纳现象中像的形态是很复杂的，例如可以在同一位置观测到多个像；可观测到单个像的伸展、收缩与倒立；观察到多像重叠；有时像是瞬息万变的.

1.2 法塔莫干纳现象成像的定性分析1.2.1 观测到多个像

如图1所示，对于一般的上现蜃景，实物发出的光线在逆温层中发生折射和全反射，人眼能观测到在实物上方形成的虚像.

当有分界面存在时，逆温层被分为一个个内部具有连续折射率梯度的小层，小层与小层之间的折射率存在明显差异，如图2所示.实物成像时，向各个方向发出光线，在每小层内部均会发生偏折，发生全反射，同一观测位置，人眼能接收到经由不同小层偏折的光线，即能看到多个像.

1.2.2 单层介质内单个像的伸展、收缩与倒立

当逆温层内部折射率随高度逐渐减小，且高度差越大时，折射率相差就越大，光线在其中的偏折角度越大.对于实物(如图4中实心黑色箭头)来说，由于其存在一定的高度，实物顶部发出的光线和实物底部发出的光线在同一小层中弯折程度不同且各个方向均存在，即会出现以下三种情况：第一种情况是形成压缩正立虚像，如图4箭头1；第二种情况是形成伸展的正立虚像，如图4箭头2，第三种情况是形成倒立虚像，如图4箭头3，其形成原因是光线在进入人眼之前已经发生交叉[2].

图4 出现3种不同形态像时的光线轨迹示意图

1.3 单层介质内的光线轨迹方程的理论推导

上述所有对成像的定性分析，均建立在光线传播路径为一条向上凸的曲线之上，为证明在折射率梯度递减介质中该轨迹的正确性，下面对光路轨迹方程进行推导.

图5为具有梯度折射率逆温层中光线轨迹示意图，横坐标为水平距离，纵坐标为竖直高度，n表示折射率.

图5 具有梯度折射率的逆温层中光线轨迹示意图

在自由扩散溶液中，折射率梯度有[3]

n(y)=n0e-λy

(1)

其中y为高度，n0为y=0处的折射率，n(y)为高度y处介质的折射率，在恒温条件下λ为常数.

由拉格朗日关系推得三维空间内光线的近轴方程[4]为

(2)

考虑二维平面内，由于折射率仅相对于高度y变化，上式进行化简为

(3)

(4)

(5)

其中θ为光线与竖直方向夹角.

(6)

解此微分方程，得

(7)

其中C1、C2由入射高度和入射角度初始值确定，恒温条件下λ为常数.在后续实验探究中，会对该方程进行验证.

2 法塔莫干纳现象的实验探究

2.1 液体中的法塔莫干纳现象及理论分析

由法塔莫干纳现象成像的定性分析可知，折射率的跃变是形成法塔莫干纳现象的必要条件，通常在空气中容易形成逆温层，但是在逆温层内折射率跃变并不容易，因此空气中的法塔莫干纳现象并不常见.本文利用液体替代空气，通过制备梯度折射率液体的方法，对空气中的法塔莫干纳现象进行了模拟再现，从而开展实验探究.为模拟实际的逆温层，选用白砂糖溶液替代空气并通过控制溶液浓度(浓度越大，折射率越大)达到形成梯度折射率及折射率跃变目的[5]；为模拟逆温层中的分界面，采用保鲜膜法，配置每小层均具有折射率梯度的分层溶液.对于法塔莫干纳现象的瞬息万变性，主要是由于实际环境中，各类外界因素使得逆温层内空气折射率每时每刻都在发生变化，实验中不予以考虑.

具体的配置方法如下：首先准备一个方形玻璃缸(30×17×20 cm3)；若干保鲜膜、烧杯、白砂糖.在4个烧杯中分别配置0.636 g/mL、0.477 g/mL、0.318 g/mL、0.159 g/mL 4种白砂糖溶液各1.5 L冷却到室温，4种溶液折射率分别为1.445、1.420、1.396、1.373.将0.636 g/mL白砂糖溶液倒入玻璃缸中，在溶液表面覆盖一层保鲜膜(玻璃缸壁上也要有一定高度的保鲜膜)，向玻璃缸中加入0.477 g/mL白砂糖溶液，溶液高度不得超过缸壁保鲜膜的高度，待两层溶液稳定后将保鲜膜缓慢抽出，抽出时尽量避免两层分界面处的晃动，再将0.318 g/mL、0.159 g/mL溶液按顺序以同样的方法加入玻璃缸中，最终形成四层明显的分层溶液，每层溶液高度均为3 cm.控制室温不变，将配好的溶液静置12 h，使溶质分子自由扩散，这样就形成了每层都具有折射率梯度、各层之间具有折射率跃变的溶液.

溶液配置完成后，在玻璃缸后8 cm处的桌面上用手机显示某一图像，相机置于玻璃缸后5 cm处拍摄蜃景，相机高度可调节.如图6所示，手机中显示的图像为adiads及图标.不断调整观测位置，可以观测到不同数量和不同形态的像.图7为利用相机拍摄的一张蜃景图，蜃景即adiads及图标.在该观测位置下，可以同时观测到5个像，蜃景中存在多像及多像重叠.例如图7中，2、3、4是单个压缩像形态，1、2、4是倒立像形态，5是正立像，这种多形态像出现即为法塔莫干纳现象.

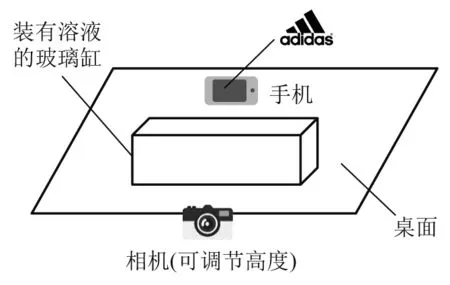
图6 观测蜃景时各物体摆放位置示意图

图7 拍摄的蜃景(共存在5个像)

而对于图7中单个像存在压缩(像2、3、4)、倒立(像1、2、4)形态，原因在于手机存在一定的高度，从该顶部发出的光线和从底部发出的光线在通过配置的多层溶液的单个小层时将发生不同程度的偏折，故而能够形成图7所示的压缩(像2、3、4)、倒立(像1、2、4)形态的像.下面通过光轨迹验证多形态像出现即法塔莫干纳现象.

图8 手机光线射入分层溶液简化模型

2.2 法塔莫干纳现象成像的实验探究

自然界中，物体向各个方向反射太阳光，肉眼无法直接看到光线轨迹，为了显示光路，方便观测，采用波长为532 nm的绿色激光代替实物发出的光线进行探究.

2.2.1 光线轨迹方程的验证

为验证光线轨迹方程的正确性，将激光(波长532 nm，绿色)照射入配置好的溶液最底层，使其在最底层发生折射和全反射.

图9为实验中拍摄的图像，对图中激光路径打点，并用1.3中式(7)函数进行拟合，如图10所示.拟合效果较好，即证明了轨迹方程的正确性.这就证实了光线在这类流体中的传播路径是一条向上凸的曲线，当物体反射的太阳光沿这种轨迹入射到人眼中时，观测者才能看到在物体上方形成的虚像.

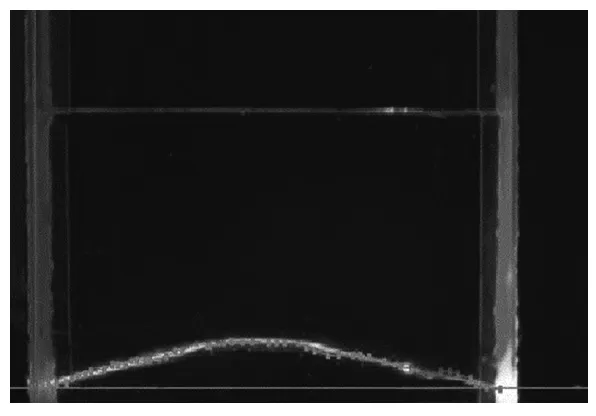
图9 在最底层发生全反射时光线轨迹

图10 函数拟合图像

2.2.2 光线弯折程度与高度的关系

利用激光笔产生绿色激光(波长532 nm)水平入射至配置好的具有折射率梯度及梯度跃变的溶液(自下而上折射率逐渐减小)中,如图11所示，图中h为激光入射点距桌面的高度，α为光线轨迹在激光出射点的切线与水平方向的夹角，即激光偏转角度.

图11 激光水平入射至溶液发生偏转

改变激光入射高度h,以模拟实物在成像时具有一定的高度，记录激光偏转角度α.以激光入射高度h为横坐标，激光偏转角度α为纵坐标作出函数图(图12).可以发现高度越高,激光偏转角度越大，这与1.2.2中提出的理论相符.

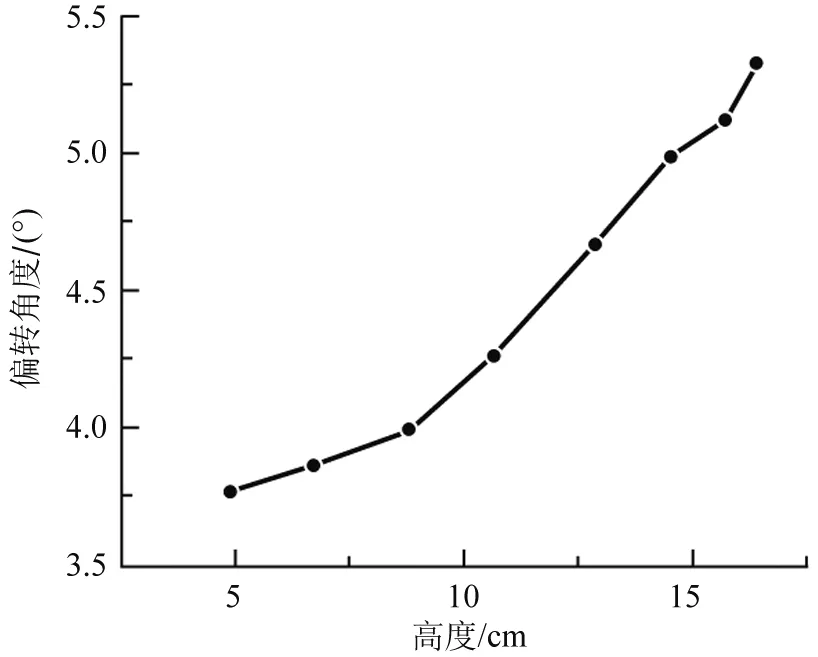
图12 激光笔入射高度与激光偏转角度的关系

结合上述对光线轨迹方程的推导验证，即可说明实物成像时，由于自身所具有的高度，顶端和底端发出的光线发生不同程度的偏折，顶端光线偏折程度较大，底部光线偏折程度较小，单个像呈现出伸展、压缩、倒立三种形态.

2.2.3 多像及多像重叠——激光入射角度对成像的影响

将激光(波长532 nm，绿色)照射入溶液中，控制激光始终从溶液最底部入射，改变激光的入射角度,以模拟实物在同一位置向各个方向发出光线(图13).记录激光入射角度θ、发生全反射的层数n、入射点到发生全反射点的水平距离L，分别以入射角度θ为横坐标，层数n及水平距离L为纵坐标作函数图(图14和图15).

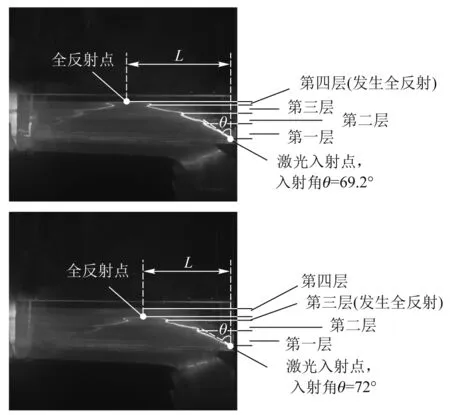
图13 改变入射角度光线在不同层发生全发射

图14 入射角度与发生全反射层数的关系

由图14可以看出，激光入射角度的大小影响发生全反射的层数，入射角度越小，发生全反射的层数越大.全反射现象存在临界角，只有当入射角超过临界角时，才会发生全反射现象，入射角度越小，越容易在小层分界面处发生折射进入更高层，在更高层溶液中发生全发射.

由图15可以看出，同一距离L对应多个入射角度.也就是物体在同一位置向不同角度发出的光线可以经由不同的小层发生全发射后进入人眼，各小层均能成像，人眼就能观测到实物形成的多个像.以L=35 cm为例，其对应图像上3个点，分别为(76.5,35)、(80.5,35)、(88.2,35)，这说明在这个观测位置能观测到3个像，其中一个像源于以76.5°角入射的光线在第二层发生全反射，另外两个像源于以80.5°和88.2°角入射的光线在第一层发生全反射.在这种情况下，人眼接收到来自第一小层和第二小层发生全反射的光线，第一小层成两个像，第二小层成一个像，三、四小层不成像.

该实验说明，实物成像时，其在同一位置发出的不同入射角度的光线在不同小层中均会发生偏折，同一观测位置能接收到来自不同小层偏折的光线，即看到多个像.这与1.2.1中给出的理论解释相符.由于物体存在一定的高度，各像之间会发生部分重叠.

图15 入射角度与水平距离的关系

3 结论

本文从理论上分析了法塔莫干纳现象出现的条件，即它需要多层内部具有折射率梯度且层与层之间折射率存在显著差异的流体作为光线的传播介质.研究结果表明，单个像的3种形态(倒立、放大、缩小)主要是由于实物自身所具有的高度使得顶端与底端发出的光线偏折程度不同而形成的；复杂性中的多像主要是由于实物发出的光线在不同层发生了偏折；多像重叠是由于实物存在一定的高度，像与像之间会部分重叠；像的瞬息万变则主要是由于实际环境中，各类外界因素使得逆温层内空气折射率每时每刻都在发生变化.